Dans quoi dessiner des images vectorielles? Pour moi, comme pour beaucoup d'autres, la réponse est assez évidente: très probablement dans l'illustrateur. Eh bien, ou dans Inskape. J'ai aussi pensé quand on m'a ordonné de dessiner huit cents pièces pour un manuel de physique. Rien de tel, juste des illustrations techniques en noir et blanc avec toutes sortes de blocs, balles, ressorts, lentilles, voitures, tracteurs, etc. Il était supposé que le livre serait composé en latech, et on m'a fourni des fichiers Word avec des images insérées - soit dans des croquis au crayon, soit dans des scans d'autres livres - et le manuscrit semblait avoir une forme quelconque. Dans ce cas, la première pensée - dessiner dans le paysage - a succombé à des fantasmes sur le sujet "comment cela automatiserait-il tout?" Pour une raison quelconque,
MetaPost semblait être la meilleure option à ce moment-là.
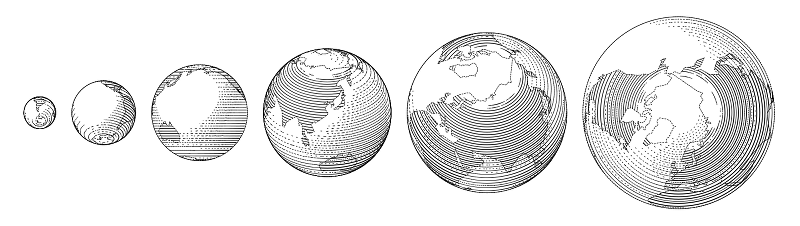
Le plus important d'une telle solution est que chaque image peut être une petite fonction de plusieurs variables; une telle image est facile, par exemple, de changer de taille et d'adapter des rayures à des circonstances spécifiques jusque-là inconnues sans violer des proportions importantes, ce qui est difficile à réaliser avec des moyens plus traditionnels. Et les éléments répétitifs - les mêmes boules et ressorts - peuvent être faits pour se comporter beaucoup plus intéressant que ne le permettent les éditeurs de vecteurs "humains".
Je voulais faire des images avec des hachures, comme celle que l'on trouve dans les vieux livres.

Tout d'abord, nous devions obtenir des lignes d'épaisseur variable. La principale difficulté ici est de construire une courbe plus ou moins parallèle à celle donnée et, si nécessaire, de changer la distance à celle donnée. Je me suis appuyé sur la
manière la plus primitive, probablement, la plus primitive par laquelle les segments reliant les points intermédiaires de la courbe de Bézier sont simplement transportés à une distance donnée en parallèle. À la différence près que cette distance peut varier le long de la courbe.
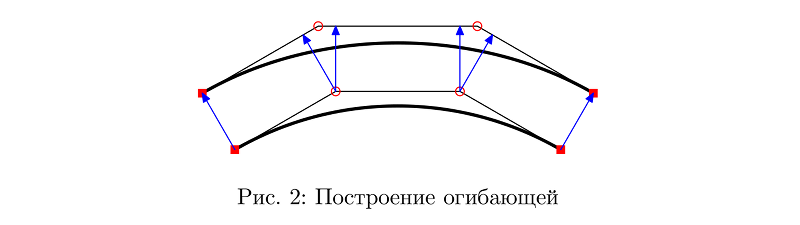
Dans la plupart des cas, cela permet un résultat décent.
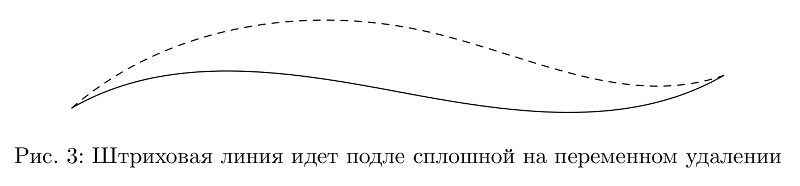
Exemple de codeCi-après, il est supposé que la bibliothèque a été
téléchargée et quelque part il y a la ligne d'
input fiziko.mp; . Le moyen le plus rapide pour démarrer et rechercher dans ConTeXt (alors
beginfig et
endfig ne
endfig pas nécessaires):
\starttext
\startMPcode
input fiziko.mp;
\stopMPcode
\stoptext
ou en LuaLaTeX:
\documentclass{article}
\usepackage{luamplib}
\begin{document}
\begin{mplibcode}
input fiziko.mp;
\end{mplibcode}
\end{document}
beginfig(3);
path p, q; % , , ,
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
q := offsetPath(p)(1cm*sin(offsetPathLength*pi)); % — , — (offsetPathLength, 0 1), ,
draw p;
draw q dashed evenly;
endfig;
Maintenant, deux de ces courbes peuvent être utilisées pour faire un contour d'une ligne d'épaisseur variable.

Exemple de codebeginfig(4);
path p, q[];
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
q1 := offsetPath(p)(1/2pt*(sin(offsetPathLength*pi)**2)); %
q2 := offsetPath(p)(-1/2pt*(sin(offsetPathLength*pi)**2)); %
fill q1--reverse(q2)--cycle;
endfig;
L'épaisseur doit être quelque peu limitée par le bas, sinon le raster prendra des parties trop fines des lignes lors de l'impression, ce qui n'est généralement pas très beau. Une option consiste à tracer toutes les lignes, dont l'épaisseur est inférieure à une certaine valeur, par des lignes en pointillés de la même épaisseur minimale, de sorte que la quantité totale de peinture par unité de longueur en moyenne corresponde à celle de la ligne de l'épaisseur cible. Autrement dit, au lieu de réduire la quantité de peinture sur les côtés de la ligne, commencez à la ronger avec des rayures transversales.

Exemple de codebeginfig(5);
path p;
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
draw brush(p)(1pt*(sin(offsetPathLength*pi)**2)); % , ,
endfig;
Vous pouvez maintenant dessiner des balles. Il peut s'agir uniquement de cercles concentriques dont l'épaisseur des lignes est déterminée par la fonction de l'éclairement de la balle aux points de passage des lignes.
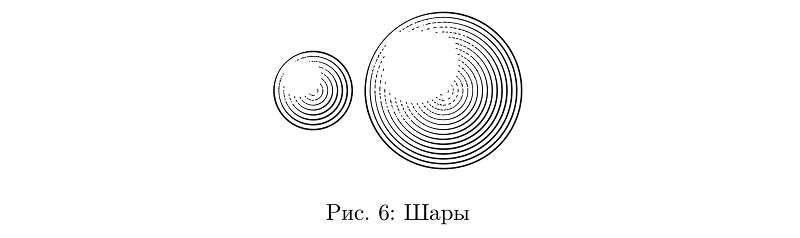
Exemple de codebeginfig(6);
draw sphere.c(1.2cm);
draw sphere.c(2.4cm) shifted (2cm, 0);
endfig;
Une autre primitive commode est les «tuyaux»: grosso modo, des cylindres qui peuvent être pliés de n'importe quelle façon. Tant qu'ils sont de section constante, tout est simple avec eux.
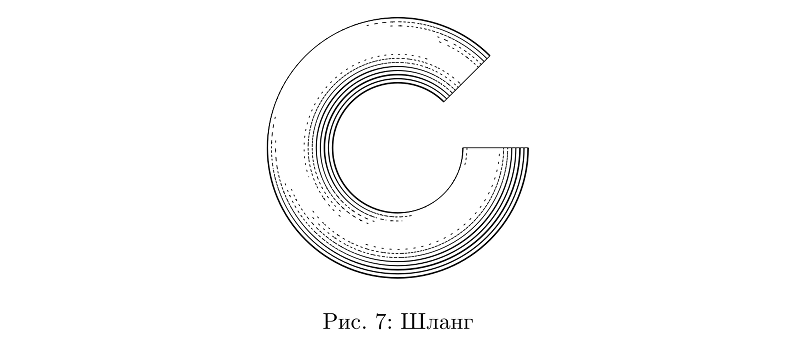
Exemple de codebeginfig(7);
path p;
p := subpath (1,8) of fullcircle scaled 3cm;
draw tube.l(p)(1/2cm); % — ,
endfig;
Si l'épaisseur change, le nombre de traits doit être modifié en conséquence, tout en maintenant la densité de remplissage moyenne inchangée, et prendre également en compte les changements d'épaisseur lors du calcul de l'éclairage.
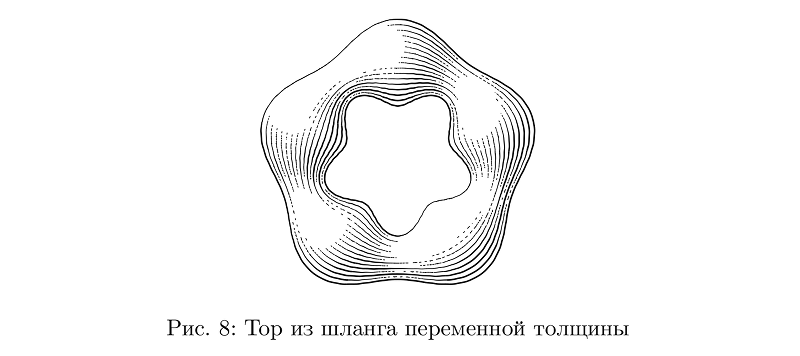
Exemple de codebeginfig(8);
path p;
p := pathSubdivide(fullcircle, 2) scaled 3cm;
draw tube.l(p)(1/2cm + 1/6cm*sin(offsetPathLength*10pi));
endfig;
Il existe encore des tuyaux à hachures transversales, mais pour eux, il était plus difficile de résoudre le problème de la préservation de la densité de remplissage moyenne, de sorte que dans de nombreux cas, ils ne semblent toujours pas très bons.
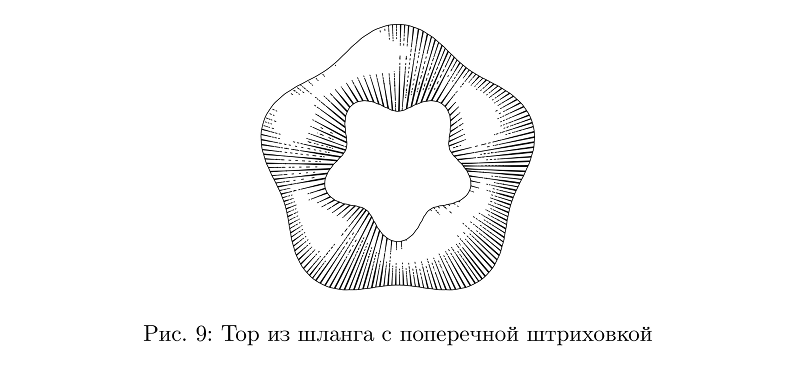
Exemple de codebeginfig(9);
path p;
p := pathSubdivide(fullcircle, 2) scaled 3cm;
draw tube.t(p)(1/2cm + 1/6cm*sin(offsetPathLength*10pi));
endfig;
En principe, beaucoup de choses peuvent être fabriquées à partir de tuyaux seuls: des cônes et des cylindres aux balustres.
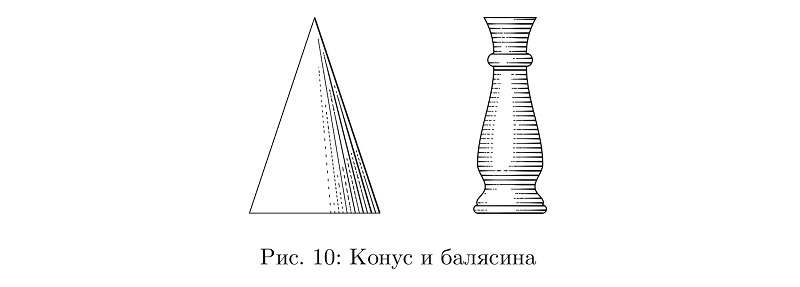
Exemple de codebeginfig(10);
draw tube.l ((0, 0) -- (0, 3cm))((1-offsetPathLength)*1cm) shifted (-3cm, 0); %
path p;
p := (-1/2cm, 0) {dir(175)} .. {dir(5)} (-1/2cm, 1/8cm) {dir(120)} .. (-2/5cm, 1/3cm) .. (-1/2cm, 3/4cm) {dir(90)} .. {dir(90)}(-1/4cm, 9/4cm){dir(175)} .. {dir(5)}(-1/4cm, 9/4cm + 1/5cm){dir(90)} .. (-2/5cm, 3cm); %
p := pathSubdivide(p, 6);
draw p -- reverse(p xscaled -1) -- cycle;
tubeGenerateAlt(p, p xscaled -1, p rotated -90); % , tube.t, — — , — .
endfig;
Une partie de ce qui peut être construit à partir de ces pièces se trouve dans la bibliothèque. Disons qu'un globe est fondamentalement une balle.
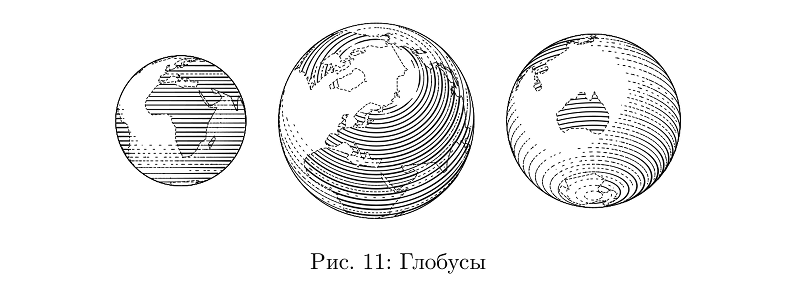
Exemple de codebeginfig(11);
draw globe(1cm, -15, 0) shifted (-6/2cm, 0); % , ,
draw globe(3/2cm, -30.28367, 59.93809);
draw globe(4/3cm, -140, -30) shifted (10/3cm, 0);
endfig;
Bien que non: ici, l'éclosion se déroule en parallèle, et le contrôle de l'épaisseur de la course pour maintenir la densité de remplissage est encore plus difficile que dans le cas de l'éclosion transversale sur les tuyaux, il s'agit donc d'un type de balle distinct.
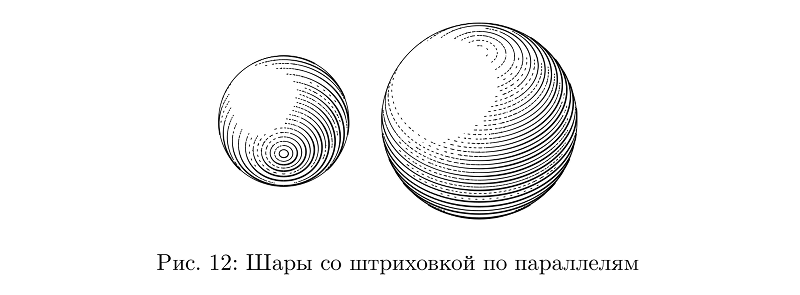
Exemple de codebeginfig(12);
draw sphere.l(2cm, -60); %
draw sphere.l(3cm, 45) shifted (3cm, 0);
endfig;
Et le poids est une conception simple de deux types de tuyaux d'épaisseur variable.
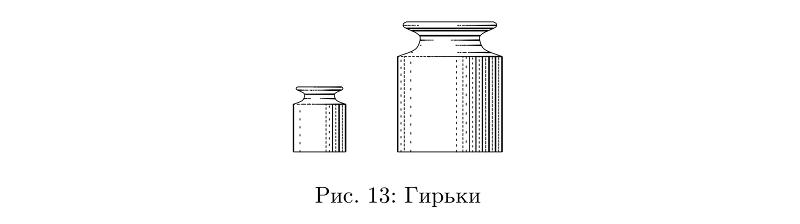
Exemple de codebeginfig(13);
draw weight.s(1cm); %
draw weight.s(2cm) shifted (2cm, 0);
endfig;
Il existe toujours un outil pour attacher les tuyaux en nœuds.
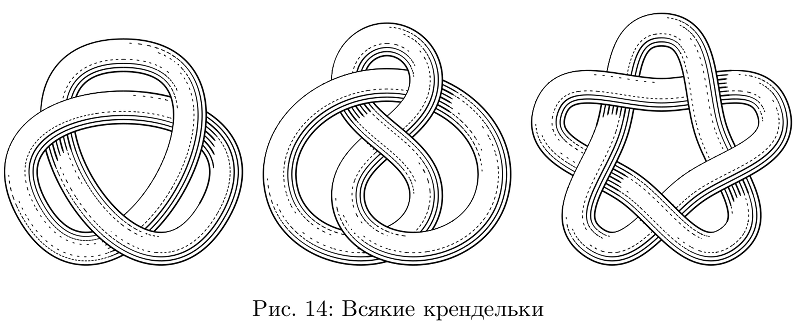
Exemple de code pour ne pas encombrer, un seul nœudbeginfig(14);
path p;
p := (dir(90)*4/3cm) {dir(0)} .. tension 3/2 ..(dir(90 + 120)*4/3cm){dir(90 + 30)} .. tension 3/2 ..(dir(90 - 120)*4/3cm){dir(-90 - 30)} .. tension 3/2 .. cycle;
p := p scaled 6/5;
addStrandToKnot (primeOne) (p, 1/4cm, "l", "1, -1, 1"); % primeOne , p 1/4cm, "l" ( tube.l, tube.t ) «» "1, -1, 1" p
draw knotFromStrands (primeOne); % .
endfig;
Les ombres des nœuds sont une complication dans le modèle d'éclairage. En principe, personne ne prend la peine de les utiliser dans d'autres cas, mais je ne me suis pas fixé pour objectif d'aller profondément dans le volume, donc même si ce n'est pas très pratique, cela ne fonctionne pas partout.
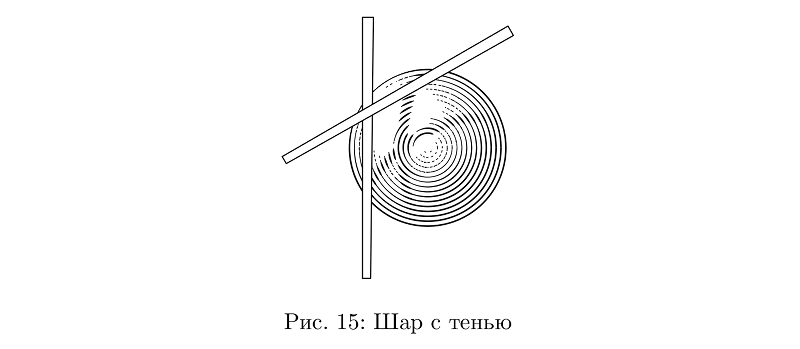
Exemple de codebeginfig(15);
path shadowPath[];
boolean shadowsEnabled;
numeric numberOfShadows;
shadowsEnabled := true; %
numberOfShadows := 1; %
shadowPath0 := (-1cm, -2cm) -- (-1cm, 2cm) -- (-1cm +1/6cm, 2cm) -- (-1cm + 1/8cm, -2cm) -- cycle; % , ,
shadowDepth0 := 4/3cm; % - «» ,
shadowPath1 := shadowPath0 rotated -60;
shadowDepth1 := 4/3cm;
draw sphere.c(2.4cm); % sphere.c tube.l
fill shadowPath0 withcolor white;
draw shadowPath0;
fill shadowPath1 withcolor white;
draw shadowPath1;
endfig;
Et, bien sûr, vous avez besoin d'une texture de bois. L'influence de la nature de la croissance des nœuds sur le motif des sections de cernes est un sujet de recherche sérieux. Très simplifiant, on peut imaginer des anneaux annuels dans des plans parallèles dans lesquels s'introduisent des distorsions des nœuds. Il suffit donc de décrire le changement dans le plan par une fonction peu sophistiquée (la fonction noeud) et de considérer une série d'isolignes pour la somme de l'ensemble de ces fonctions comme le modèle souhaité d'anneaux d'arbre.
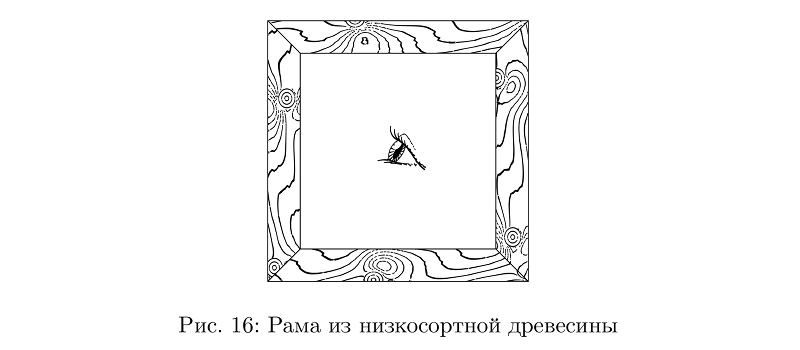
Exemple de codebeginfig(16);
numeric w, b;
pair A, B, C, D, A', B', C', D';
w := 4cm;
b := 1/2cm;
A := (0, 0);
A' := (b, b);
B := (0, w);
B' := (b, wb);
C := (w, w);
C' := (wb, wb);
D := (w, 0);
D' := (wb, b);
draw woodenThing(A--A'--B'--B--cycle, 0); % , A--A'--B'--B--cycle, 0
draw woodenThing(B--B'--C'--C--cycle, 90);
draw woodenThing(C--C'--D'--D--cycle, 0);
draw woodenThing(A--A'--D'--D--cycle, 90);
eyescale := 2/3cm; %
draw eye(150) shifted 1/2[A,C]; % 150
endfig;
L'œil de l'image ci-dessus peut s'ouvrir légèrement, puis plisser les yeux, et la largeur de la pupille change. Il n'y a pas de signification particulière à cela, mais cela s'avère plus vivant que si de telles bagatelles étaient mécaniquement les mêmes partout.

Exemple de codebeginfig(17);
eyescale := 2/3cm; % 1/2cm
draw eye(0) shifted (0cm, 0);
draw eye(0) shifted (1cm, 0);
draw eye(0) shifted (2cm, 0);
draw eye(0) shifted (3cm, 0);
draw eye(0) shifted (4cm, 0);
endfig;
Le plus souvent, les images n'étaient pas très compliquées, mais si vous abordez la question avec sérieux, de nombreuses tâches doivent être résolues afin de les illustrer de manière significative. Ici, disons, la tâche de Lopital sur le bloc (je ne sais pas comment on l'appelle correctement en russe, ce n'était pas dans le manuel, c'est juste pour un exemple): le bloc est suspendu à une corde de longueur l suspendue au point A, il est accroché à une autre corde suspendu à la même hauteur au point B, la cargaison C est suspendue à la deuxième corde. La question est, si les cordes et le bloc sont en apesanteur, où sera la cargaison? Étonnamment, la solution du problème et la construction ne sont pas si élémentaires, mais, en jouant avec plusieurs variables, vous pouvez facilement faire l'image exactement ce qui sera le mieux sur la bande, tout en restant vrai.
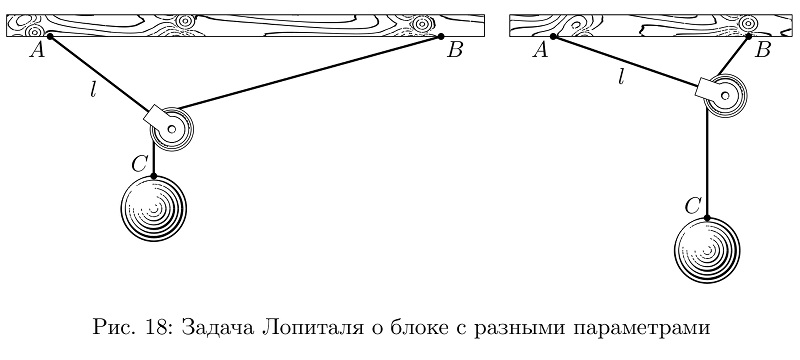
Exemple de codevardef lHopitalPulley (expr AB, l, m) = % AB l, m . ? : , , arithmetic overflow.
save A, B, C, D, E, o, a, x, y, d, w, h, support;
image(
pair A, B, C, D, E, o[];
path support;
numeric a, x[], y[], d[], w, h;
x1 := (l**2 + abs(l)*((sqrt(8)*AB)++l))/4AB; % ,
y1 := l+-+x1; %
y2 := m - ((AB-x1)++y1); %
A := (0, 0);
B := (AB*cm, 0);
D := (x1*cm, -y1*cm);
C := D shifted (0, -y2*cm);
d1 := 2/3cm; d2 := 1cm; d3 := 5/6d1; % ,
w := 2/3cm; h := 1/3cm; % . ,
o1 := (unitvector(CD) rotated 90 scaled 1/2d3);
o2 := (unitvector(DB) rotated 90 scaled 1/2d3);
E := whatever [D shifted o1, C shifted o1]
= whatever [D shifted o2, B shifted o2]; % ,
a := angle(AD);
support := A shifted (-w, 0) -- B shifted (w, 0) -- B shifted (w, h) -- A shifted (-w, h) -- cycle;
draw woodenThing(support, 0); % ,
draw pulley (d1, a - 90) shifted E; %
draw image(
draw A -- D -- B withpen thickpen;
draw D -- C withpen thickpen;
) maskedWith (pulleyOutline shifted E); %
draw sphere.c(d2) shifted C shifted (0, -1/2d2); %
dotlabel.llft(btex $A$ etex, A);
dotlabel.lrt(btex $B$ etex, B);
dotlabel.ulft(btex $C$ etex, C);
label.llft(btex $l$ etex, 1/2[A, D]);
)
enddef;
beginfig(18);
draw lHopitalPulley (6, 2, 11/2); % ,
draw lHopitalPulley (3, 5/2, 3) shifted (8cm, 0);
endfig;
Qu'est-ce qu'un manuel? Hélas et ah, quand presque toutes les illustrations et la mise en page étaient prêtes, quelque chose s'est passé là-bas et il n'est jamais sorti. Par conséquent, probablement, quelque temps plus tard, j'ai réécrit toutes les choses principales de la bibliothèque résultante et j'ai
posté le code sur le github . Certains kunshtyuki n'y sont pas entrés: par exemple, des circuits électriques ou une fonction pour dessiner des voitures et des tracteurs. Certains - ajouté: nœuds, par exemple.
Toute cette cuisine ne fonctionne pas rapidement: il faut environ une minute pour rassembler toutes les photos de cet article avec LuaLaTeX sur mon ordinateur portable avec le i5-4200U 1,6 GHz. Pour tant de choses, un générateur de nombres pseudo-aléatoires est utilisé, donc des images similaires seront un peu différentes non seulement à l'intérieur d'un cycle (c'est une fonctionnalité), mais chaque cycle suivant donnera des images différentes du précédent. Mais vous pouvez toujours définir
randomseed := - dans le préambule, et toutes les mêmes exécutions produiront les mêmes images.