En fait, il est le plus. Mais tout d'abord.
Énoncé du problème
Je maîtrise le python, je résous tout sur Codewars. Je rencontre une tâche bien connue concernant un gratte-ciel et des œufs. La seule différence est que les données source ne sont pas 100 étages et 2 œufs, mais un peu plus.
Compte tenu de: N œufs, M tente de les jeter, gratte-ciel sans fin.
Définissez: le plancher maximum à partir duquel vous pouvez jeter un œuf sans casser. Les œufs sont sphériques dans le vide et, si l'un d'eux ne casse pas, tombant, par exemple, du 99e étage, les autres résisteront également à une chute de tous les étages de moins d'un centième.
0 <= N, M <= 20 000.
Le temps d'exécution de deux douzaines de tests est de 12 secondes.
Rechercher une solution
Nous devons écrire une hauteur de fonction (n, m), qui renverra le numéro d'étage pour le n, m donné. Puisqu'il sera mentionné très souvent, et à chaque fois que vous écrivez la paresse «en hauteur», puis partout, sauf pour le code, je le désignerai comme f (n, m).
Commençons par des zéros. Évidemment, s'il n'y a pas d'œufs ou de tentatives de les jeter, rien ne peut être déterminé et la réponse sera zéro.
f (0, m) = 0, f (n, 0) = 0.Supposons qu'il y ait un œuf et qu'il y ait 10 tentatives. Vous pouvez tout risquer et le jeter tout de suite du centième étage, mais en cas d'échec, vous ne pourrez rien déterminer d'autre, il est donc plus logique de partir du premier étage et de monter d'un étage après chaque lancer, jusqu'à ce que la tentative ou l'œuf se termine. Le maximum où vous pouvez obtenir si l'œuf ne tombe pas est le numéro 10. 10.
f (1, m) = mPrenez le deuxième œuf, essayez à nouveau 10. Maintenant, alors vous pouvez tenter votre chance avec un centième? S'il se casse, il y aura encore une et 9 tentatives, au moins 9 étages pourront passer. Alors peut-être devez-vous risquer non pas à partir du centième, mais à partir du dixième? Est logique. Ensuite, en cas de succès, 2 œufs et 9 tentatives resteront. Par analogie, vous devez maintenant monter encore 9 étages. Avec une série de succès - encore 8, 7, 6, 5, 4, 3, 2 et 1. Au total, nous sommes au 55e étage avec deux œufs entiers et sans essayer. La réponse est la somme des M premiers membres de la progression arithmétique avec le premier membre 1 et l'étape 1.
f (2, m) = (m * m + m) / 2 . Il est également clair qu'à chaque étape la fonction f (1, m) a été appelée, mais ce n'est pas encore exact.
Continuez avec trois œufs et dix tentatives. En cas d'échec d'un premier lancer, les étages couverts par 2 œufs et 9 tentatives seront couverts par le bas, ce qui signifie que le premier lancer doit être effectué à partir du sol f (2, 9) + 1. Ensuite, en cas de succès, nous avons 3 œufs et 9 tentatives . Et pour la deuxième tentative, vous devez monter d'un autre f (2,8) + 1 étages. Et ainsi de suite, jusqu'à ce qu'il reste 3 œufs et 3 tentatives sur les mains. Et puis il est temps de se laisser distraire en considérant les cas avec N = M, quand il y a autant d'œufs qu'il y a de tentatives.
Et en même temps ceux où il y a plus d'oeufs.Mais ici, tout est évident - des œufs au-delà de ceux qui se cassent ne nous seront pas utiles, même si chaque lancer est infructueux. f (n, m) = f (m, m) si n> m . Et dans l'ensemble, 3 œufs, 3 lancers. Si le premier œuf se casse, vous pouvez vérifier f (2, 2) étages en bas, et s'il ne casse pas, alors f (3,2) étages en haut, c'est-à-dire le même f (2, 2). Total f (3, 3) = 2 * f (2, 2) + 1 = 7. Et f (4, 4), par analogie, consistera en deux f (3, 3) et un, et ce sera 15. Tous il ressemble aux puissances de deux, et nous écrivons: f (m, m) = 2 ^ m - 1 .
Cela ressemble à une recherche binaire dans le monde physique: nous partons de l'étage numéro 2 ^ (m-1), en cas de succès nous montons 2 ^ (m-2) étages, et en cas d'échec, nous descendons autant, et ainsi de suite, jusqu'à ce que les tentatives s'épuisent. Dans notre cas, nous nous levons tout le temps.
Revenons à f (3, 10). En fait, à chaque étape, tout se résume à la somme f (2, m-1) - le nombre d'étages qui peut être déterminé en cas de défaillance, les unités et f (3, m-1) - le nombre d'étages qui peut être déterminé en cas de succès. Et il devient clair que de l'augmentation du nombre d'œufs et de tentatives, il est peu probable que quelque chose change.
f (n, m) = f (n - 1, m - 1) + 1 + f (n, m - 1) . Et c'est une formule universelle qui peut être implémentée en code.
from functools import lru_cache @lru_cache() def height(n,m): if n==0 or m==0: return 0 elif n==1: return m elif n==2: return (m**2+m)/2 elif n>=m: return 2**n-1 else: return height(n-1,m-1)+1+height(n,m-1)
Bien sûr, auparavant, je suis monté sur le râteau des fonctions récursives non-mémorisation et j'ai découvert que f (10, 40) prend près de 40 secondes avec le nombre d'appels à lui-même - 97806983. Mais la mémorisation ne sauvegarde également qu'aux intervalles initiaux. Si f (200,400) est exécuté en 0,8 seconde, alors f (200, 500) est déjà en 31 secondes. C'est drôle que lorsque vous mesurez le temps d'exécution à l'aide de% timeit, le résultat est bien moins réel que réel. De toute évidence, la première exécution de la fonction prend la plupart du temps, tandis que les autres utilisent simplement les résultats de sa mémorisation. Mensonges, mensonges flagrants et statistiques.
La récursivité n'est pas nécessaire, nous regardons plus loin
Ainsi, dans les tests, par exemple, f (9477, 10000) apparaît, mais mon pathétique f (200, 500) ne correspond plus au bon moment. Il existe donc une autre solution, sans récursivité, nous allons poursuivre sa recherche. J'ai complété le code en comptant les appels de fonction avec certains paramètres afin de voir dans quoi il s'est finalement décomposé. Pour 10 tentatives, les résultats suivants ont été obtenus:
f (3,10) = 7+ 1 * f (2,9) + 1 * f (2,8) + 1 * f (2,7) + 1 * f (2,6) + 1 * f (2 , 5) + 1 * f (2,4) + 1 * f (2,3) + 1 * f (3,3)
f (4,10) = 27+ 1 * f (2,8) + 2 * f (2,7) + 3 * f (2,6) + 4 * f (2,5) + 5 * f (2 , 4) + 6 * f (2,3) + 6 * f (3,3) + 1 * f (4,4)
f (5,10) = 55+ 1 * f (2,7) + 3 * f (2,6) + 6 * f (2,5) + 10 * f (2,4) + 15 * f (2 , 3) + 15 * f (3,3) + 5 * f (4,4) + 1 * f (5,5)
f (6,10) = 69+ 1 * f (2,6) + 4 * f (2,5) + 10 * f (2,4) + 20 * f (2,3) + 20 * f (3 , 3) + 10 * f (4,4) + 4 * f (5,5) + 1 * f (6,6)
f (7,10) = 55+ 1 * f (2,5) + 5 * f (2,4) + 15 * f (2,3) + 15 * f (3,3) + 10 * f (4 , 4) + 6 * f (5,5) + 3 * f (6,6) + 1 * f (7,7)
f (8,10) = 27+ 1 * f (2,4) + 6 * f (2,3) + 6 * f (3,3) + 5 * f (4,4) + 4 * f (5 , 5) + 3 * f (6,6) + 2 * f (7,7) + 1 * f (8,8)
f (9,10) = 7+ 1 * f (2,3) + 1 * f (3,3) + 1 * f (4,4) + 1 * f (5,5) + 1 * f (6 , 6) + 1 * f (7,7) + 1 * f (8,8) + 1 * f (9,9)
Une certaine régularité est visible:

Ces coefficients sont calculés théoriquement. Chaque bleu est la somme du haut et de la gauche. Et les violettes sont les mêmes bleues, seulement dans l'ordre inverse. Vous pouvez calculer, mais c'est encore une récursivité, et j'ai été déçu. Très probablement, beaucoup (c'est dommage que ce ne soit pas moi) ont déjà appris ces chiffres, mais pour l'instant je vais continuer l'intrigue, en suivant ma propre solution. J'ai décidé de cracher dessus et d'aller de l'autre côté.
Il ouvrit l'exel, construisit une assiette avec les résultats de la fonction et commença à chercher des motifs. C3 = IF (C $ 2> $ B3; 2 ^ $ B3-1; C2 + B2 + 1), où $ 2 est la ligne avec le nombre d'oeufs (1-13), $ B est la colonne avec le nombre de tentatives (1-20), C3 - cellule à l'intersection de deux œufs et d'une tentative.
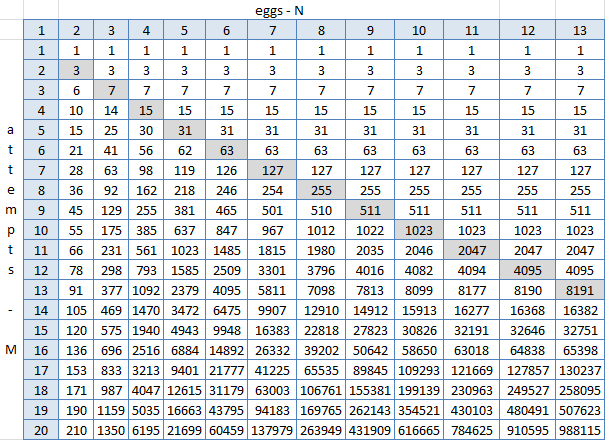
La diagonale grise est N = M, et ici on voit clairement qu'à sa droite (pour N> M) rien ne change. On peut le voir - mais il ne peut en être autrement, car ce sont tous les résultats du travail de la formule, dans lequel il est donné que chaque cellule est égale à la somme du haut, du haut à gauche et d'une. Mais une formule universelle où vous pouvez remplacer N et M et obtenir le numéro d'étage n'a pas été trouvée. Spoiler: il n'existe pas. Mais alors c'est si simple de créer ce tableau dans Excel, peut-être est-il possible de générer le même python et d'en faire glisser les réponses?
Numpy vous n'avez pas
Je me souviens qu'il y a NumPy, qui est juste conçu pour fonctionner avec des tableaux multidimensionnels, pourquoi ne pas l'essayer? Pour commencer, nous avons besoin d'un tableau unidimensionnel de zéros de taille N + 1 Et d'un tableau unidimensionnel d'unités de taille N.Prenez le premier tableau de zéro à l'avant-dernier élément, ajoutez-le élément par élément avec le premier tableau du premier élément au dernier et avec un tableau d'unités. Au tableau résultant, ajoutez zéro au début. Répétez M fois. L'élément numéro N du tableau résultant sera la réponse. Les 3 premières étapes ressemblent à ceci:
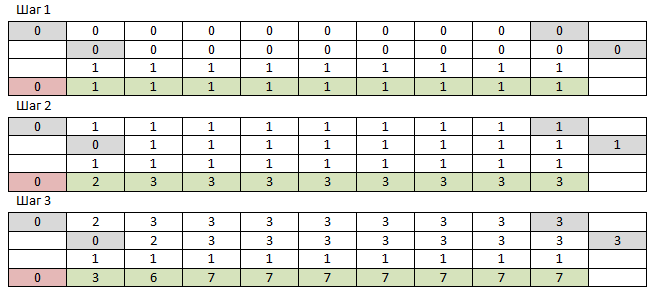
NumPy fonctionne si vite que je n'ai pas enregistré la table entière - chaque fois que je relis la ligne nécessaire. Une chose - le résultat du travail sur de grands nombres était faux. Les rangs supérieurs sont comme ceux-là, tandis que les rangs inférieurs ne le sont pas. Voici à quoi ressemblent les erreurs arithmétiques des nombres à virgule flottante accumulées à partir de plusieurs ajouts. Peu importe - vous pouvez changer le type du tableau en int. Non, problème - il s'est avéré que, pour des raisons de vitesse, NumPy ne fonctionne qu'avec ses types de données, et son int, contrairement à Python int, ne peut pas dépasser 2 ^ 64-1, après quoi il déborde silencieusement et continue avec -2 ^ 64. Et je m'attends à des nombres inférieurs à trois mille caractères. Mais cela fonctionne très rapidement, f (9477, 10000) fonctionne sur 233 ms, il s'avère juste une sorte de non-sens à la sortie. Je ne donnerai même pas le code, car une telle chose. J'essaierai d'en faire un python propre.
Itéré, itéré, mais pas itéré
def height(n, m): arr = [0]*(n+1) while m > 0: arr = [0] + list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) m-=1 return arr[n]
44 secondes pour calculer f (9477, 10000), c'est un peu trop. Mais absolument sûr. Qu'est-ce qui peut être optimisé? Tout d'abord, il n'est pas nécessaire de tout considérer à droite de la diagonale M, M. La seconde - pour considérer le dernier tableau dans son ensemble, pour le bien d'une cellule. Pour cela, les deux dernières deux cellules de la précédente conviendront. Pour calculer f (10, 20), seules ces cellules grises suffiront:
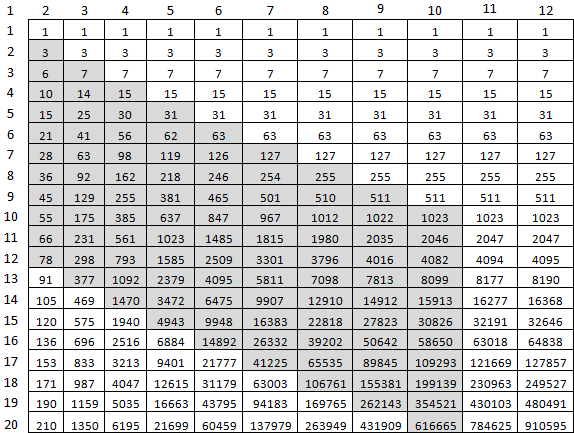
Et donc ça regarde dans le code:
def height(n, m): arr = [0, 1, 1] i = 1 while i < n and i < mn:
Et qu'en pensez-vous? f (9477, 10000) en 2 secondes! Mais cette entrée est trop bonne, la longueur du tableau à n'importe quel stade ne dépassera pas 533 éléments (10000-9477). Vérifions f (5477, 10000) - 11 secondes. C'est aussi bien, mais seulement en comparaison avec 44 secondes - vingt tests avec ce temps ne passeront pas.
Ce n'est pas ça. Mais puisqu'il y a une tâche, alors il y a une solution, la recherche continue. J'ai recommencé à regarder le tableau Excel. La cellule à gauche de (m, m) est toujours une de moins. Et la cellule à gauche de celle-ci n'est plus là, dans chaque rangée la différence devient plus grande. La cellule en dessous (m, m) est toujours deux fois plus grande. Et la cellule en dessous n'est plus deux fois, mais légèrement plus petite, mais pour chaque colonne différemment, plus elle est grande, plus elle est grande. Et aussi les nombres sur une ligne au début augmentent rapidement, et après le milieu lentement. Permettez-moi de construire un tableau des différences entre les cellules voisines, peut-être quel modèle apparaîtra là-bas?
Plus chaud
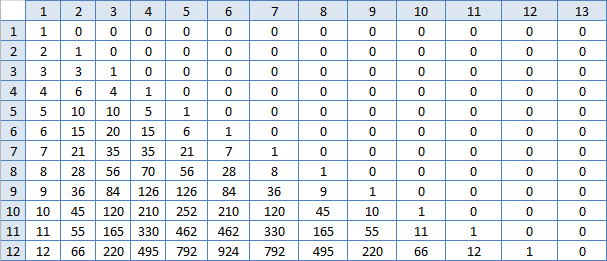
Bah, des chiffres familiers! Autrement dit, la somme N de ces nombres dans la ligne numéro M est-ce la réponse? Certes, les compter est à peu près le même que ce que j'ai déjà fait, il est peu probable que cela accélère considérablement le travail. Mais vous devez essayer:
f (9477, 10000): 17 secondes def height(n, m): arr = [1,1] while m > 1: arr = [1] + list(map(lambda x,y: x+y, arr[1:], arr[:-1])) + [1] m-=1 return sum(arr[1:n+1])
Ou 8, si vous ne comptez que la moitié du triangle def height(n, m): arr = [1,1] while m > 2 and len(arr) < n+2:
Pour ne pas dire qu'une solution plus optimale. Cela fonctionne plus rapidement sur certaines données, plus lentement sur certaines. Nous devons aller plus loin. Quel est ce triangle avec des nombres apparus deux fois dans la solution? C'est dommage d'admettre, mais j'ai oublié en toute sécurité les mathématiques supérieures, où le triangle doit avoir figuré, j'ai donc dû le google.
Bingo!
Le triangle de Pascal , comme on l'appelle officiellement. Tableau des coefficients binomiaux infinis. La réponse au problème avec N œufs et M lancers est donc la somme des N premiers coefficients dans l'expansion du binôme de Newton du Mième degré, à l'exception du zéro.
Un coefficient binomial arbitraire peut être calculé à partir des factorielles du numéro de ligne et du numéro de coefficient dans la ligne: bk = m! / (N! * (Mn!)). Mais la meilleure partie est que vous pouvez calculer séquentiellement les nombres dans la chaîne, en connaissant son nombre et son coefficient zéro (toujours un): bk [n] = bk [n-1] * (m - n + 1) / n. À chaque étape, le numérateur diminue d'une unité et le dénominateur augmente. Et la solution finale concise ressemble à ceci:
def height(n, m): h, bk = 0, 1
33 ms au calcul de f (9477, 10000)! Cette solution peut également être optimisée, bien que dans les gammes données et cela fonctionne bien. Si n se trouve dans la seconde moitié du triangle, alors nous pouvons l'inverser en mn, calculer la somme des n premiers coefficients et la soustraire de 2 ^ m-2. Si n est proche du milieu et m est impair, les calculs peuvent également être réduits: la somme de la première moitié de la ligne sera 2 ^ (m-1) -1, le dernier coefficient de la première moitié peut être calculé par factorielles, son nombre est (m-1) / 2, puis continuez à ajouter des coefficients si n est dans la moitié droite du triangle, ou soustrayez s'il est à gauche. Si m est pair, vous ne pouvez pas compter la moitié de la ligne, mais vous pouvez trouver la somme des premiers coefficients m / 2 + 1 en calculant la moyenne par factorielle et en ajoutant la moitié à 2 ^ (m-1) -1. Sur les données d'entrée de l'ordre de 10 ^ 6, cela réduit très sensiblement le temps d'exécution.
Après une décision réussie, j'ai commencé à chercher les recherches de quelqu'un d'autre sur cette question, mais je n'ai trouvé que la même chose, à partir des entretiens, avec seulement deux œufs, et ce n'est pas du sport. Internet sera incomplet sans ma décision, j'ai décidé, et le voici.