Julia. Connaissance

Ode à Julia

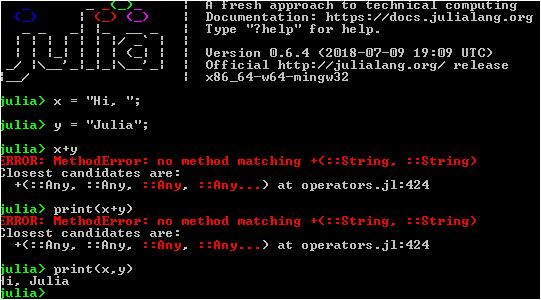
Il est très difficile de transmettre tout l'enthousiasme qui a accompagné le lancement des premiers programmes et la correction des premières erreurs en utilisant ce langage. Simple et beau comme Python , un peu comme Fortran , un travail pratique avec des tableaux et des graphiques, ainsi que la possibilité d'effectuer une optimisation et une parallélisation féroces même pour les nuls tels que je mes camarades de classe. Vous pouvez travailler à différents niveaux d'abstraction: de la programmation de haut niveau au typage dynamique, vous pouvez descendre jusqu'aux commandes assembleur, c'est-à-dire que vous avez ici à la fois l'accessibilité Python et la vitesse d'exécution des compteurs Fortran. Je ne peux pas me débarrasser du sentiment que Mathcad , Scilab et même, Dieu me pardonne, le C ++ commence à s'estomper dans mon cœur.

J'ai appris la langue en tombant par hasard sur une publication de Khabrovian et, comme un étudiant impressionnable le devrait, j'ai commencé à chercher des conseils, de préférence en russe. Depuis que la langue évolue constamment depuis six ans, les sources d'information déjà rares sont devenues obsolètes et l'excitation a commencé à diminuer. Mais avec le début d'un nouveau cours de laboratoire sur la modélisation des phénomènes physiques avec le libre choix d'un langage de programmation, il y avait toujours une motivation pour commencer à faire connaissance avec Julia. De plus, en août, le langage "add up 1.0" .

Le matériel présenté ci-dessous a été conçu comme une introduction à la langue dans laquelle tous les articles de laboratoire ont été rédigés et un manuel de formation a été collecté.

Julia est un langage de programmation de typage dynamique de haut niveau et hautes performances pour les calculs mathématiques. La syntaxe est similaire à la famille matlab, le langage est écrit en C , C ++ et Scheme , il est possible d'appeler les bibliothèques Sysh

L'installation

Eh bien, tout s'est finalement installé, maintenant à notre disposition:

• Invite de commandes JuliaPRO - toutes les compétences Yulina directement à partir de l'interprète.
• Juno est un bel IDE avec une fenêtre pour les graphiques et un espace de travail où vous pouvez voir le contenu de tous les objets
• Jupyter - lance le noyau informatique dans la console et vous pouvez exécuter le code directement dans le navigateur. (En plus de Julia, Python est également présent)

Voyons ce que cette calculatrice peut faire ... Prise en charge Unicode - vous pouvez utiliser l'alphabet cyrillique, les hiéroglyphes et appeler pi la lettre grecque. Et vous ne pouvez pas spécifier explicitement la multiplication entre le nombre et la variable (dans cet ordre et sans espace):

x = 5+8 2x - 3x + 2x^2 Out: 325 

Tous les panneaux nécessaires sont également en place: + =, * =, >> =, etc. (Signe ">>" (décalage de bit vers la droite). Signe de comparaison:>,> =, <, <=, ==,! =. Les inégalités peuvent être combinées en chaînes:

 y = 5 y += 2 4 <= y < 8 Out: true 

Numéros complexes disponibles:

 (2-1im)*(4+3im) Out: 11 + 2im 

Et des fonctions pour travailler avec eux:

• réel (z) est la partie réelle,
• imag (z) est la partie imaginaire,
• conj (z) est le conjugué complexe,
• abs (z) - module,
• abs2 (z) est le carré du module,
• angle (z) est l'argument d'un nombre complexe.

Vous pouvez utiliser des nombres rationnels en utilisant "//" et les fonctions correspondantes:

• num (x) - numérateur,
• den (x) - dénominateur,
• float (x) - convertit en décimal

 x = 4//6+5//7 Out: 29//21 float(x) Out: 1.380952380952381 

Julia a la capacité de contrôler la représentation interne des données:

• typeof (obj) - type d'objet
• typemax (obj) est le nombre maximum de ce type
• typemin (obj) - minime
• eps () - zéro machine
• BigInt est un grand tout
• BigFloat - grande virgule flottante

 q = 3 typemax(q) Out: 9223372036854775807 typeof(q) Out: Int64 BigFloat(2.3^45/6) Out: 3.159376405019356000000000000000000000000000000000000000000000000000000000000e+15 

Les fonctions

Kit de fonctionnalités

• abs (x) est le module d'un nombre,
• abs2 (x) est le carré du module,
• sqrt (x) est la racine carrée,
• cbrt (x) est la racine cubique,
• exp (x) est l'exposant du nombre,
• log (x) est le logarithme naturel,
• log10 (x) - logarithme décimal,
• log (b, x) est le logarithme de x à la base b.
  Ainsi que trigonométrique, hyperbolique, Airy, Bessel et bien d'autres.

Fonctions personnalisées:

 function () #  end 

La fonction renvoie le résultat de la dernière expression (utilisateur Mathcad hoqueté).

 function cube(x) x^3 end cube(4) Out: 64 

Eh bien, ou nous indiquons explicitement:

 function myabs(x) if x>=0 return x else return -x end end myabs(-12) Out: 12 

Les valeurs retournées peuvent être collectées dans un tuple:

 function cubeandsquare(x) x^3,x^2 end a,b = cubeandsquare(3) print("a = $a, b = $b") Out: a = 27, b = 9 

Les fonctions peuvent prendre des tuples, des valeurs par défaut, des mots-clés. S'il n'y a pas de crochets après le nom de la fonction, il est considéré comme une variable et peut être affecté à une autre variable ou transféré à la fonction en tant que paramètre. Julia prend également en charge un style fonctionnel de programmes d'écriture (bonjour Lisp)

 function mysin(t;A=1,?=1,?=0) #   -     A*sin(?*t + ?) end x1 = mysin(pi) #   = 0 x2 = mysin(pi*0.5,A = 2) #      x3 = mysin(pi*0.5,? = 0.5) #      print("x1 = $x1, x2 = $x2, x3 = $x3") Out: x1 = 1.2246467991473532e-16, x2 = 2.0, x3 = 0.7071067811865475 

Tableaux

En tant qu'utilisateur Scilab , je n'ai même pas remarqué la substitution: vous pouvez spécifier un tableau en utilisant la fonction:

• Array {T} (undef, dims ...) - Un tableau de type T et dimension dims
• zéros (T, dims ...) - Tableau de zéros
• ceux (T, dims ...) - ou unités
  L'indexation commence par un , au lieu de $ - end , et toutes les opérations nécessaires pour les matrices sont définies (pour effectuer, par exemple, une addition ou une multiplication élément par élément, vous devez placer un point devant l'opérateur).

(Maintenant, il est clair comment insérer des images, mais d'accord ...)

Fonctions de base:

• det (A) - calculer le déterminant
• A ' - transposer la matrice
• inv (A) - matrice inversée
• longueur (A) - nombre d'éléments
• ndims (A) - nombre de dimensions
• taille (A) - tuple de dimensions
• taille (A, n) - dimension dans une direction donnée
• copy (A) - crée une copie du tableau
• linspace (début, fin, étape) ou
  linspace (start: step: end) - crée un tableau unidimensionnel

 A = [1 2 3; 6 5 4; 7 8 9] Out: 3?3 Array{Int64,2}: 1 2 3 6 5 4 7 8 9 A[2,1] Out: 6 A[end] Out: 9 size(A) Out: (3, 3) 

Vous pouvez sélectionner des parties du tableau en spécifiant une plage d'indices le long de la dimension avec le signe ":".

 m1 = rand(3,2) m2 = reshape(1:2:11, 3,2) Out: 3?2 Base.ReshapedArray{Int64,2,StepRange{Int64,Int64},Tuple{}}: 1 7 3 9 5 11 m3 = [m1 m2] #   (  ) Out: 3?4 Array{Float64,2}: 0.325649 0.701038 1.0 7.0 0.513579 0.620215 3.0 9.0 0.815242 0.805307 5.0 11.0 m5 = [m1; m2] #   (  ) Out: 6?2 Array{Float64,2}: 0.325649 0.701038 0.513579 0.620215 0.815242 0.805307 1.0 7.0 3.0 9.0 5.0 11.0 m3[:, 2:4] Out: 3?3 Array{Float64,2}: 0.701038 1.0 7.0 0.620215 3.0 9.0 0.805307 5.0 11.0 

Ici, nous avons utilisé rand (), qui retourne un tableau de nombres aléatoires d'une dimension donnée, et reshape (), qui change la dimension du tableau en celle spécifiée.

 for a in A #   a   A end 

ou

 for i in eachindex(A) #     i end 

ou

 for i = 1 : size(A,n) # n -      (..    ) #     i end 

Graphiques

Pour utiliser des graphiques, vous devez télécharger un package à partir du référentiel pour choisir parmi:

• Pkg.add ("Tracés")
• Pkg.add ("PyPlot")
• Pkg.add ("Gadfly")
• Pkg.add ("Winston")

Parmi ceux-ci, le plus populaire est le PyPlot Pythonic. Les modules sont connectés à l'aide de la commande, par exemple:

 using PyPlot 

Cependant, essayons Gaston en utilisant Gnuplot (swing séparément).
Chargé par l'équipe Gaston.jl

  Pkg.add("Gaston") 

Et droit au but:

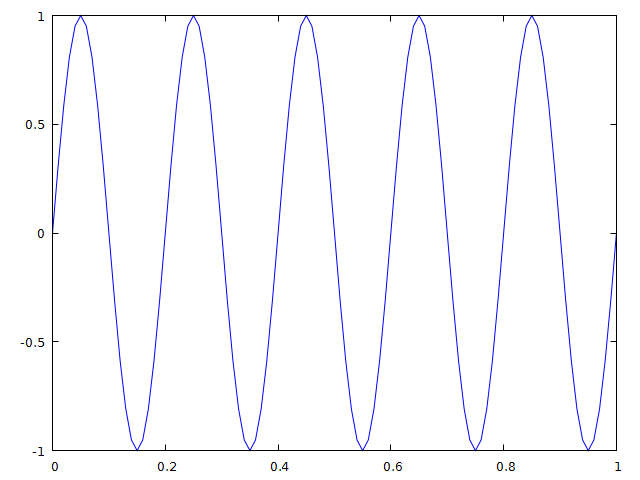
 using Gaston t = 0:0.01:1 plot(t, sin.(2?*5*t)) 

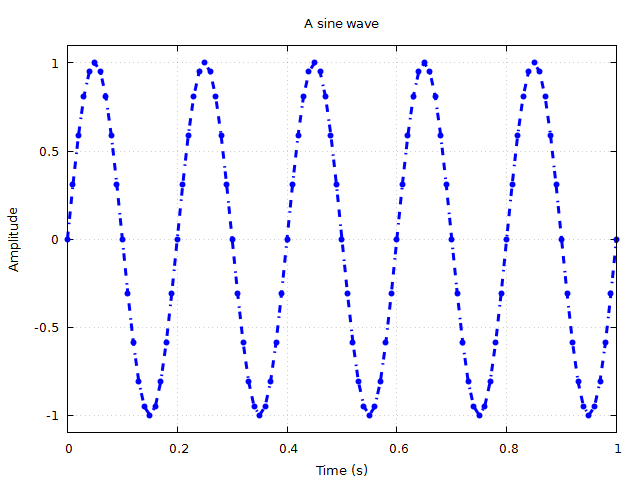
 plot(t,sin.(2?*5*t),title="A sine wave",xlabel="Time (s)",ylabel="Amplitude",grid="on",linewidth=3,color="blue", yrange="[-1.1:1.1]",marker="ecircle",plotstyle="linespoints",linestyle="-.-") 

 plot!(t,cos.(2?*5*t),color="red",linewidth=2) #       

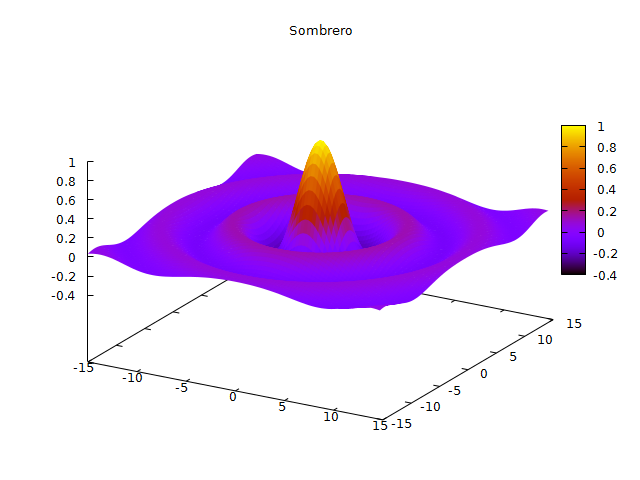
 x = y = -15:0.33:15 surf(x,y,(x,y)->sin.(sqrt.(x.*x+y.*y))./sqrt.(x.*x+y.*y),title="Sombrero",plotstyle="pm3d") 

 x = y = -15:0.33:15 surf(x,y,(x,y)->sin.(sqrt(x.*x+y.*y))./sqrt.(x.*x+y.*y), title="Edge view of a sombrero",plotstyle="pm3d",gpcom="set view 80,20") 

 R = [ x+y for x=0:5:120, y=0:5:120] G = [ x+y for x=0:5:120, y=120:-5:0] B = [ x+y for x=120:-5:0, y=0:5:120] Z = zeros(25,25,3) Z[:,:,1] = R Z[:,:,2] = G Z[:,:,3] = B imagesc(Z,title="RGB Image",clim=[10 200]) 

 histogram(rand(1000),bins=15,norm=1,title="Histogram",yrange="[0:1.6]") 

 y = 1:40 err = Gaston.ErrorCoords(rand(40)) plot(y,err=err,title="Example of error bars",plotstyle="errorbars") 

Vous pouvez créer plusieurs fenêtres graphiques (ne fonctionne pas dans Jupyter ) à l'aide de la commande h = figure () (il suffit de l'insérer entre les graphiques). Pour enregistrer le graphique en tant que fichier image, utilisez les commandes
set_filename ("name.png") # si non spécifié, sera affiché
printfigure ("png") # enregistrer dans un fichier, PNG, PDF, SVG et GIF disponibles
Plus d'informations sur le forfait Gaston

Conclusion

Il existe de nombreux autres packages graphiques pour tous les goûts et couvrant presque tous les besoins. De plus, des packages auxiliaires se développent avec might et main. Ici, vous avez l'informatique quantique, la bioinformatique et l'apprentissage automatique, et bien d'autres problèmes urgents comme les diffurs et les dérivés .

En général, Julia est belle, intelligente et très prometteuse, et il est extrêmement inadmissible de la laisser sans attention.