Cet article discute des similitudes et des différences entre les deux approches pour résoudre les problèmes algorithmiques:
la programmation dynamique (programmation dynamique) et le principe de
«diviser pour régner» (diviser et conquérir). Nous comparerons en utilisant deux algorithmes comme exemple:
la recherche binaire (comment trouver rapidement un nombre dans un tableau trié) et
la distance de Levenshtein (comment convertir une ligne en une autre avec un nombre minimum d'opérations).
Je tiens à noter tout de suite que cette comparaison et explication ne prétend pas être extrêmement correcte. Et peut-être même que certains professeurs d'université voudraient m'expulser :) Cet article est juste ma tentative personnelle de trier les choses et de comprendre ce qu'est la programmation dynamique et comment le principe de «diviser pour mieux régner» est impliqué.Alors commençons ...
Le problème
Quand j'ai
commencé à étudier les algorithmes, il m'était difficile de comprendre l'idée de base de la programmation dynamique (ci-après
DP , de Dynamic Programming) et en quoi elle diffère de l'approche «diviser pour régner» (plus loin
DC , pour diviser et conquérir). Lorsqu'il s'agit de comparer ces deux paradigmes,
beaucoup utilisent avec succès la fonction Fibonacci pour illustrer. Et c'est une excellente illustration. Mais il me semble que lorsque nous utilisons
la même tâche pour illustrer DP et DC, nous perdons un détail important qui peut nous aider à rattraper plus rapidement la différence entre les deux approches. Et ce détail est que ces deux techniques se manifestent le mieux dans la résolution de
différents types de problèmes.
Je suis toujours en train d'apprendre le DP et le DC et je ne peux pas dire que j'ai complètement compris ces concepts. Mais j'espère toujours que cet article apportera un éclairage supplémentaire et aidera à franchir la prochaine étape dans l'étude d'approches importantes telles que la programmation dynamique et le diviser pour mieux régner.
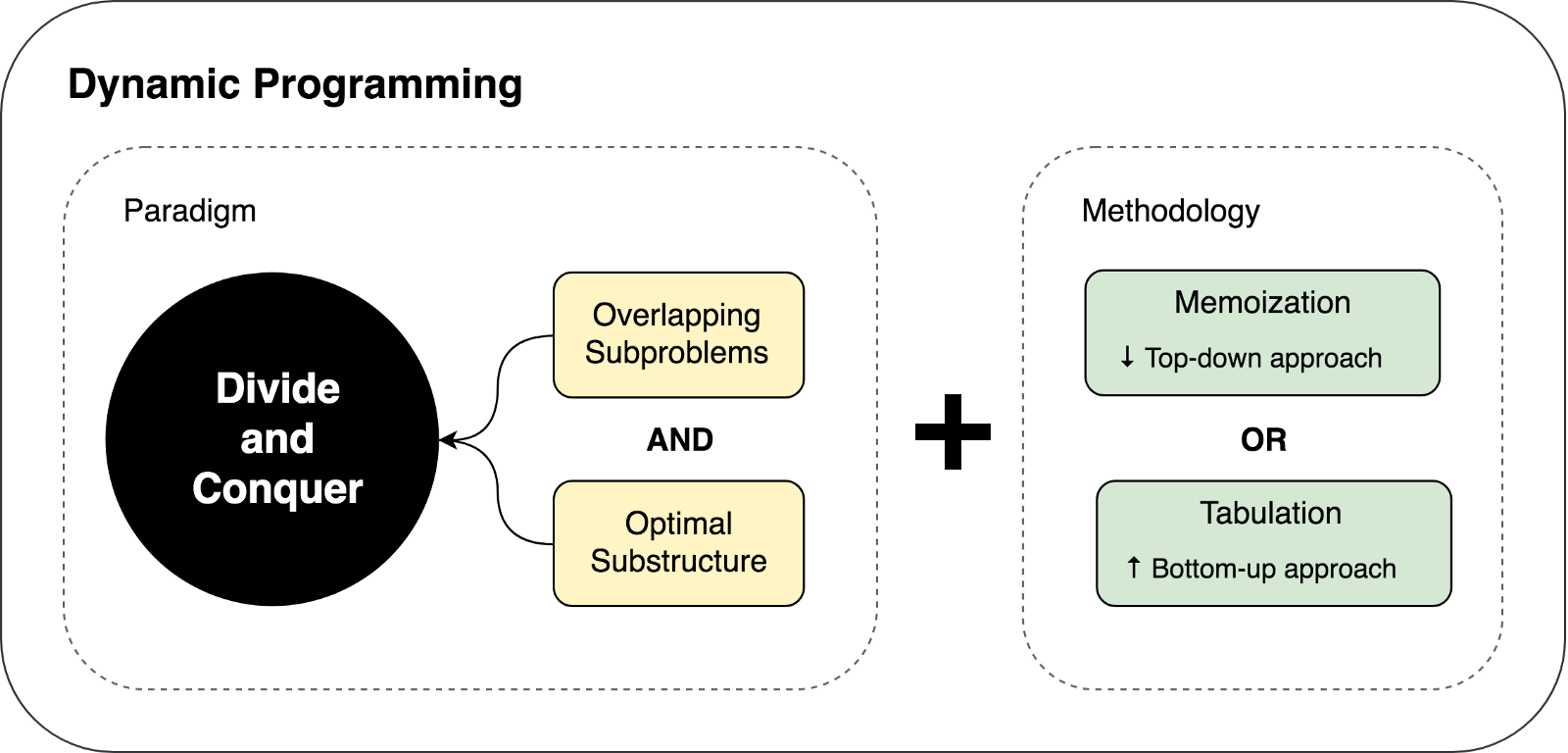
Similitudes entre DP et DC
La façon dont je vois ces deux concepts maintenant, je peux conclure que
DP est une version étendue de DC .
Je
ne les considérerais
pas comme quelque chose de complètement différent. Parce que ces deux concepts
divisent récursivement un problème en deux ou plusieurs sous-problèmes du même type jusqu'à ce que ces sous-problèmes soient assez faciles à résoudre directement. De plus, toutes les solutions au sous-problème sont combinées afin de donner finalement une réponse au problème original et original.
Alors, pourquoi avons-nous encore deux approches différentes (DP et DC) et pourquoi j'ai appelé la programmation dynamique une extension. En effet, la programmation dynamique peut être appliquée à des tâches qui présentent certaines
caractéristiques et limitations . Et seulement dans ce cas, DP étend DC en
utilisant deux techniques: la
mémorisation et la
tabulation .
Allons un peu plus loin dans les détails ...
Limitations et caractéristiques nécessaires à une programmation dynamique
Comme nous venons de le découvrir, il existe deux caractéristiques clés qu'une tâche / un problème doit avoir pour que nous puissions le résoudre à l'aide de la programmation dynamique:
- Sous-structure optimale - il devrait être possible de composer une solution optimale à un problème d'une solution optimale à ses sous-tâches.
- Sous-problèmes croisés - le problème doit être décomposé en sous-problèmes, qui à leur tour sont réutilisés à plusieurs reprises. En d'autres termes, une approche récursive pour résoudre le problème impliquerait une solution multiple (et non une seule) au même sous-problème, au lieu de produire des sous-problèmes nouveaux et uniques dans chaque cycle récursif.
Dès que nous pouvons trouver ces deux caractéristiques dans le problème que nous considérons, nous pouvons dire qu'il peut être résolu en utilisant la programmation dynamique.
La programmation dynamique comme extension du principe de "diviser pour mieux régner"
DP étend DC avec l'aide de deux techniques (
mémorisation et
tabulation ), dont le but est de sauvegarder des solutions aux sous-problèmes pour leur future réutilisation. Ainsi, les solutions sont mises en cache par sous-problème, ce qui conduit à une amélioration significative des performances de l'algorithme. Par exemple, la complexité temporelle d'une implémentation récursive «naïve» de la fonction de Fibonacci est
O(2 n ) . Dans le même temps, une solution basée sur la programmation dynamique est exécutée en seulement
(n) .
La mémorisation (remplir le cache de haut en bas) est une technique de mise en cache qui utilise des solutions nouvellement calculées pour les sous-tâches. La fonction de Fibonacci utilisant la technique de mémorisation ressemblerait à ceci:
memFib(n) { if (mem[n] is undefined) if (n < 2) result = n else result = memFib(n-2) + memFib(n-1) mem[n] = result return mem[n] }
La tabulation (remplissage du cache de bas en haut) est une technique similaire, mais qui se concentre principalement sur le remplissage du cache, et non sur la recherche d'une solution au sous-problème. Le calcul des valeurs qui doivent être mises en cache est plus facile dans ce cas à effectuer de manière itérative, plutôt que récursive. La fonction de Fibonacci utilisant la technique de tabulation ressemblerait à ceci:
tabFib(n) { mem[0] = 0 mem[1] = 1 for i = 2...n mem[i] = mem[i-2] + mem[i-1] return mem[n] }
Vous pouvez en savoir plus sur la comparaison de la mémorisation et de la tabulation
ici .
L'idée principale qui doit être prise dans ces exemples est que puisque nos problèmes DC ont des sous-problèmes qui se chevauchent, nous pouvons utiliser la mise en cache des solutions aux sous-problèmes en utilisant l'une des deux techniques de mise en cache: la mémorisation et la tabulation.
Alors, quelle est la différence entre DP et DC à la fin
Nous avons découvert les limites et les conditions préalables à l'utilisation de la programmation dynamique, ainsi que les techniques de mise en cache utilisées dans l'approche DP. Essayons de résumer et de décrire les pensées ci-dessus dans l'illustration suivante:
Essayons de résoudre quelques problèmes en utilisant DP et DC pour démontrer ces deux approches en action.
Exemple de division et de conquête: recherche binaire
L' algorithme de recherche
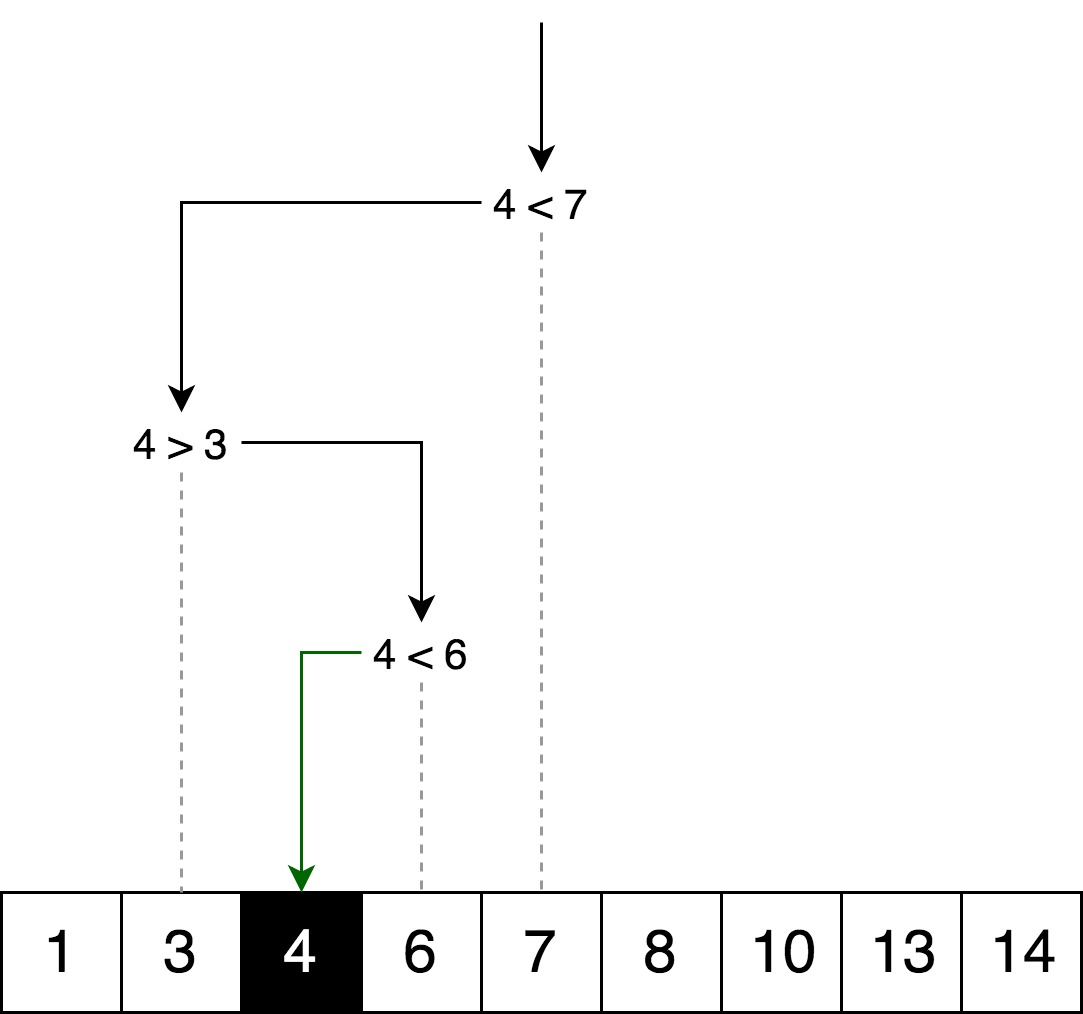
binaire est un algorithme de recherche qui trouve la position de l'élément demandé dans un tableau trié. En recherche binaire, nous comparons la valeur de la variable avec la valeur de l'élément au milieu du tableau. S'ils ne sont pas égaux, alors la moitié du tableau dans lequel l'élément souhaité ne peut pas être exclu d'une recherche ultérieure. La recherche se poursuit dans la moitié du tableau, dans laquelle la variable souhaitée peut être localisée jusqu'à ce qu'elle soit trouvée. Si la moitié suivante du tableau ne contient pas d'éléments, la recherche est considérée comme terminée et nous concluons que le tableau ne contient pas la valeur souhaitée.
ExempleL'illustration ci-dessous est un exemple de recherche binaire du nombre 4 dans un tableau.
Représentons la même logique de recherche, mais sous la forme d'un «arbre de décision».
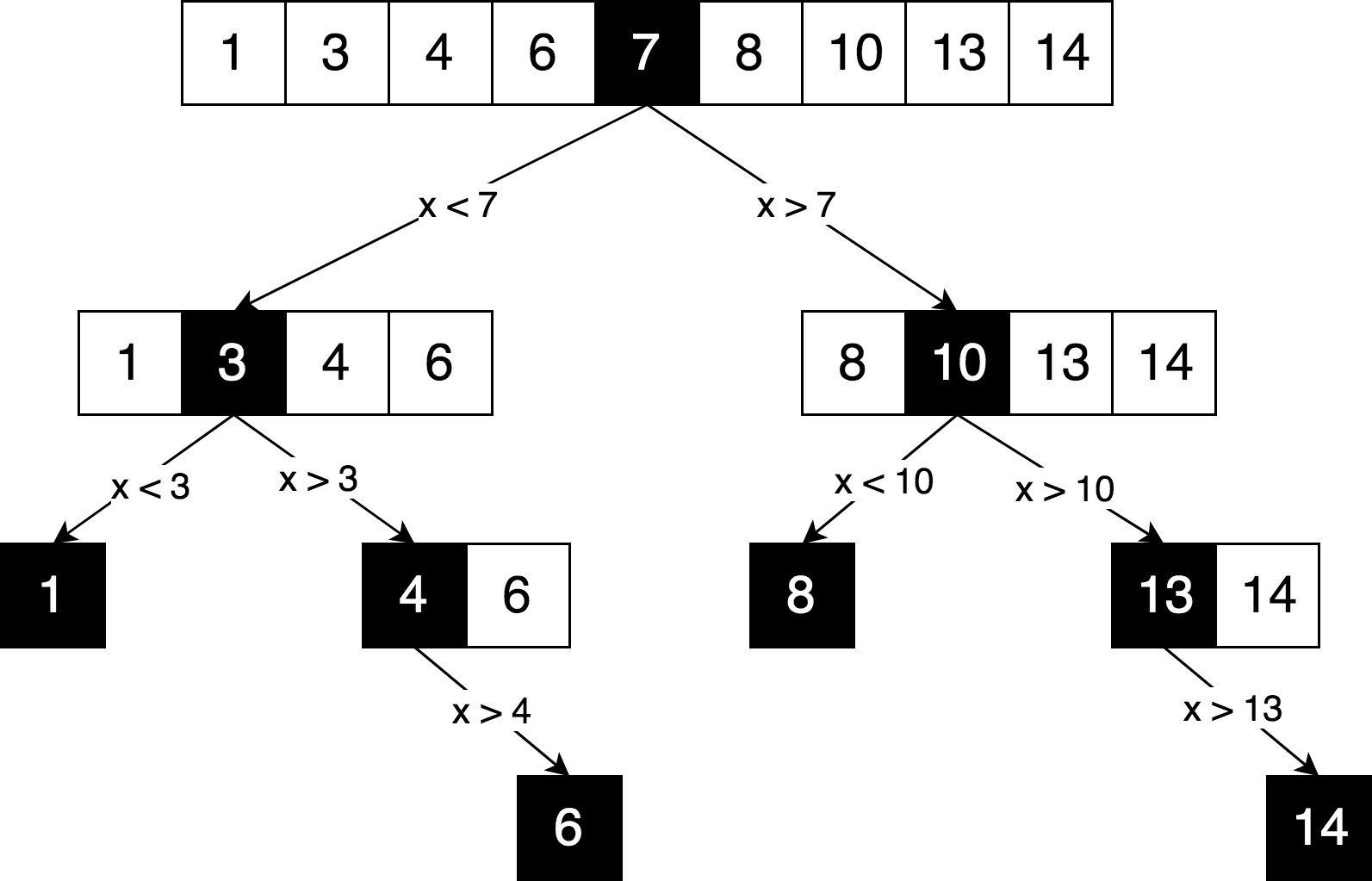
Vous pouvez voir dans ce diagramme un principe clair de «diviser pour régner», utilisé pour résoudre ce problème. Nous divisons de manière itérative notre tableau d'origine en sous-tableaux et essayons de trouver l'élément que nous recherchons déjà en eux.
Pouvons-nous résoudre ce problème en utilisant la programmation dynamique?
Non. Pour la raison que cette tâche
ne contient pas de sous-problèmes qui se croisent . Chaque fois que nous divisons un tableau en parties, les deux parties sont complètement indépendantes et ne se chevauchent pas. Et selon les hypothèses et les limites de la programmation dynamique dont nous avons discuté ci-dessus, les sous-problèmes doivent en quelque sorte se chevaucher, ils
doivent être répétitifs .
Habituellement, chaque fois qu'un arbre de décision ressemble exactement à un
arbre (et
non à un graphique ), cela signifie très probablement qu'il n'y a pas de sous-problèmes qui se chevauchent,
Implémentation d'algorithmeIci vous pouvez trouver le code source complet de l'algorithme de recherche binaire avec des tests et des explications.
function binarySearch(sortedArray, seekElement) { let startIndex = 0; let endIndex = sortedArray.length - 1; while (startIndex <= endIndex) { const middleIndex = startIndex + Math.floor((endIndex - startIndex) / 2);
Exemple de programmation dynamique: modification de la distance
Habituellement, lorsqu'il s'agit d'expliquer la programmation dynamique,
la fonction Fibonacci est utilisée comme exemple. Mais dans notre cas, prenons un exemple un peu plus complexe. Plus il y a d'exemples, plus il est facile de comprendre le concept.
La distance d'édition (ou la distance Levenshtein) entre deux lignes est le nombre minimum d'opérations pour insérer un caractère, supprimer un caractère et remplacer un caractère par un autre, nécessaire pour transformer une ligne en une autre.
ExemplePar exemple, la distance d'édition entre les mots «chaton» et «assis» est de 3, car vous devez effectuer trois opérations d'édition (deux remplacements et un insert) afin de convertir une ligne en une autre. Et il est impossible de trouver une option de conversion plus rapide avec moins d'opérations:
- chaton → sitten (remplacer «k» par «s»)
- sitten → sittin (en remplaçant «e» par «i»)
- sittin → assis (insérer complètement «g»).
Application d'algorithmeL'algorithme a un large éventail d'applications, par exemple pour la vérification orthographique, les systèmes de correction de reconnaissance optique, la recherche de chaîne inexacte, etc.
Définition mathématique d'un problèmeMathématiquement, la distance de Levenstein entre deux lignes
a, b (respectivement de longueurs | a | et
|b| ) est déterminée par la fonction
function lev(|a|, |b|) , où:
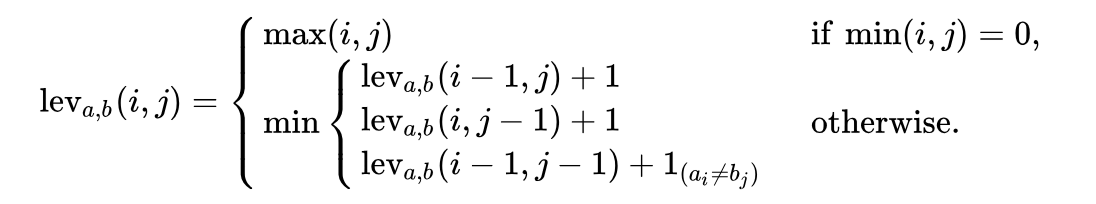
Veuillez noter que la première ligne de la fonction
min correspond à l'opération de
suppression , la deuxième ligne correspond à l'opération d'
insertion et la troisième ligne correspond à l'opération de
remplacement (dans le cas où les lettres ne sont pas égales).
ExplicationEssayons de comprendre ce que cette formule nous dit. Prenons un exemple simple pour trouver la distance de montage minimale entre les lignes
ME et
MY . Intuitivement, vous savez déjà que la distance de montage minimale est une (
1 ) opération de remplacement (remplacez «E» par «Y»). Mais formalisons notre solution et transformons-la en une forme algorithmique, afin de pouvoir résoudre des versions plus complexes de ce problème, comme la transformation du mot
samedi en
dimanche .
Afin d'appliquer la formule à la transformation ME → MY, nous devons d'abord trouver la distance d'édition minimale entre ME → M, M → MY et M → M. Ensuite, nous devons choisir le minimum de trois distances et y ajouter une opération (+1) de la transformation E → Y.
On voit donc déjà le caractère récursif de cette solution: la distance d'édition minimale ME → MY est calculée à partir des trois transformations possibles précédentes. Ainsi, nous pouvons déjà dire qu'il s'agit d'un algorithme de division et de conquête.
Pour expliquer davantage l'algorithme, plaçons nos deux lignes dans une matrice:
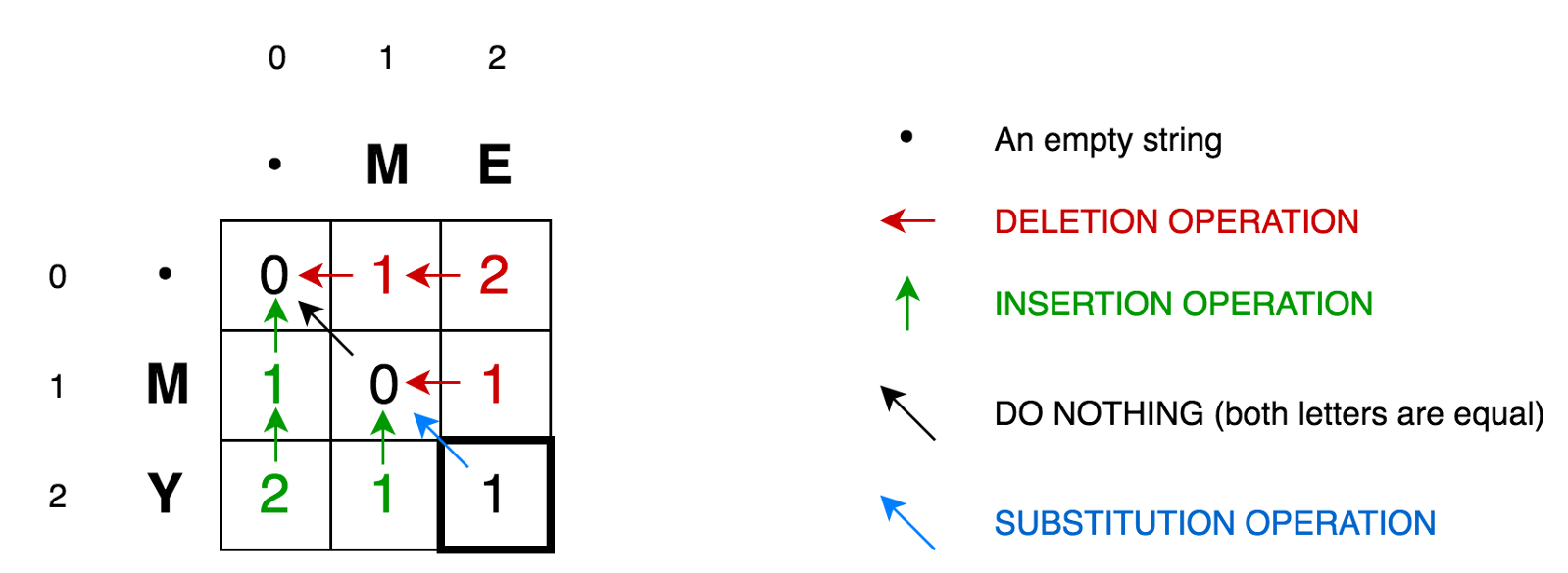La cellule (0,1) contient le nombre rouge 1. Cela signifie que nous devons effectuer 1 opération pour convertir M en une chaîne vide - supprimer M. Par conséquent, nous avons marqué ce nombre en rouge.
La cellule (0,2) contient un nombre rouge 2. Cela signifie que nous devons effectuer 2 opérations afin de transformer la chaîne ME en une chaîne vide - supprimer E, supprimer M.
La cellule (1,0) contient un nombre vert 1. Cela signifie que nous avons besoin d'une opération pour transformer une chaîne vide en M - coller M. Nous avons marqué l'opération d'insertion en vert.
La cellule (2,0) contient un nombre vert 2. Cela signifie que nous devons effectuer 2 opérations afin de convertir une chaîne vide en une chaîne MY - insérer Y, insérer M.
La cellule (1,1) contient le nombre 0. Cela signifie que nous n'avons besoin d'aucune opération pour convertir la chaîne M en M.
La cellule (1,2) contient le numéro rouge 1. Cela signifie que nous devons effectuer 1 opération pour transformer la chaîne ME en M - supprimer E.
Et ainsi de suite ...
Cela ne semble pas difficile pour les petites matrices, comme la nôtre (seulement 3x3). Mais comment calculer les valeurs de toutes les cellules pour les grandes matrices (par exemple, pour une matrice 9x7 dans la transformation samedi → dimanche)?
La bonne nouvelle est que, selon la formule, tout ce dont nous avons besoin pour calculer la valeur de n'importe quelle cellule avec les coordonnées
(i,j) est juste les valeurs de 3 cellules voisines
(i-1,j) ,
(i-1,j-1) et
(i,j-1) . Tout ce que nous devons faire est de trouver la valeur minimale de trois cellules voisines et d'ajouter un (+1) à cette valeur si nous avons des lettres différentes dans la i-ème ligne et la j-ème colonne.
Encore une fois, vous pouvez clairement voir la nature récursive de cette tâche.
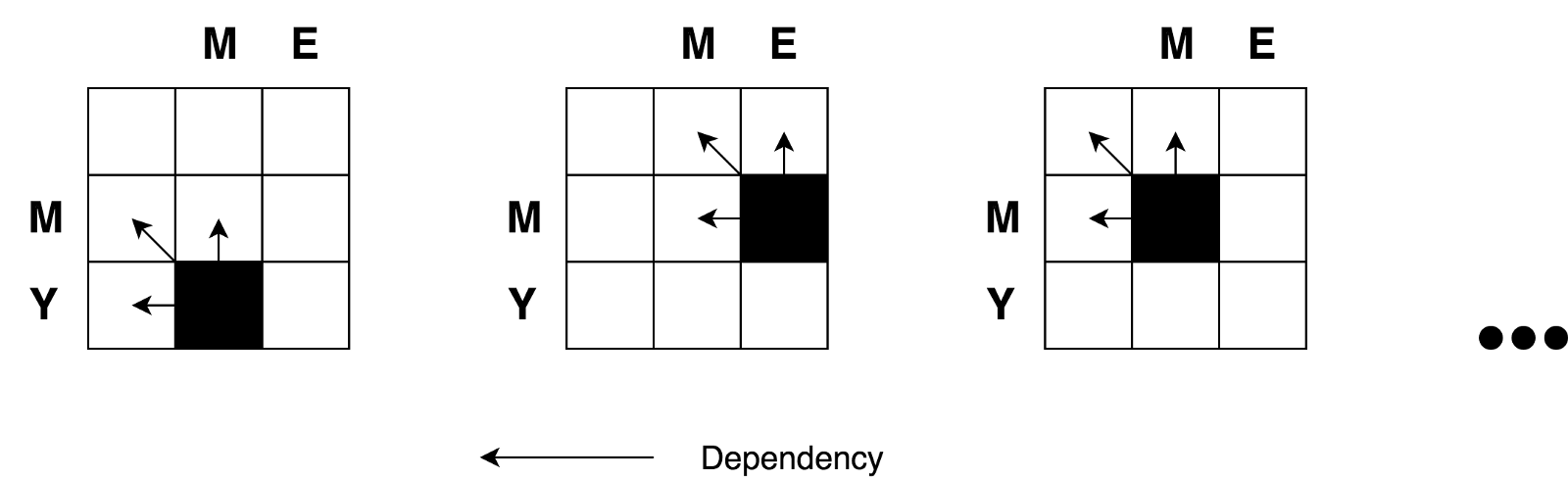
Nous avons également vu que nous avions affaire à une tâche de division et de conquête. Mais, pouvons-nous appliquer une programmation dynamique pour résoudre ce problème? Cette tâche satisfait-elle aux conditions de «
problèmes croisés » et de «
sous-structures optimales » mentionnées ci-dessus?
Oui Construisons un arbre de décision.
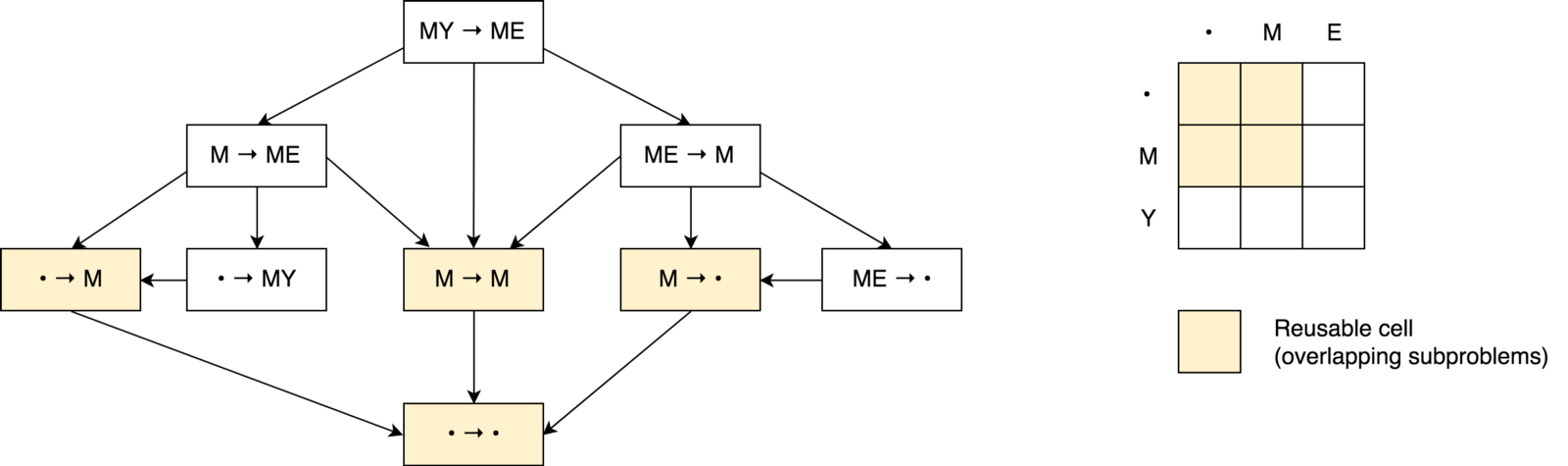
Tout d'abord, vous remarquerez peut-être que notre arbre de décision ressemble plus à un
graphique de décision qu'à un
arbre . Vous pouvez également remarquer
plusieurs sous-tâches qui se chevauchent . On voit également qu'il est impossible de réduire le nombre d'opérations et de le rendre inférieur au nombre d'opérations de ces trois cellules voisines (sous-problèmes).
Vous pouvez également remarquer que la valeur de chaque cellule est calculée en fonction des valeurs précédentes. Ainsi, dans ce cas, la technique de
tabulation est utilisée (remplissage du cache dans le sens ascendant). Vous le verrez dans l'exemple de code ci-dessous.
En appliquant tous ces principes, nous pouvons résoudre des problèmes plus complexes, par exemple, la tâche de transformation samedi → dimanche:
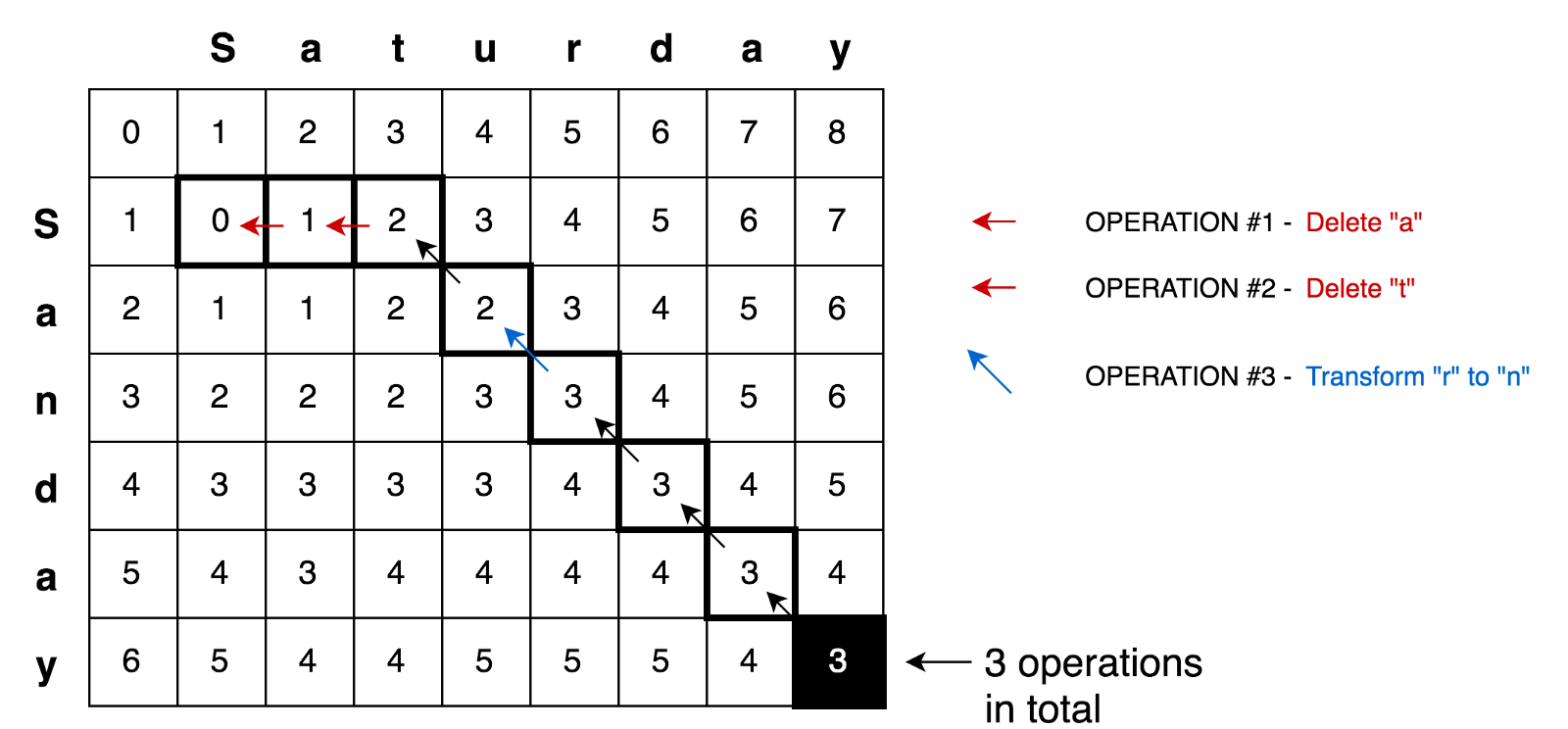Exemple de codeIci vous pouvez trouver une solution complète pour trouver la distance de montage minimale avec des tests et des explications:
function levenshteinDistance(a, b) { const distanceMatrix = Array(b.length + 1) .fill(null) .map( () => Array(a.length + 1).fill(null) ); for (let i = 0; i <= a.length; i += 1) { distanceMatrix[0][i] = i; } for (let j = 0; j <= b.length; j += 1) { distanceMatrix[j][0] = j; } for (let j = 1; j <= b.length; j += 1) { for (let i = 1; i <= a.length; i += 1) { const indicator = a[i - 1] === b[j - 1] ? 0 : 1; distanceMatrix[j][i] = Math.min( distanceMatrix[j][i - 1] + 1,
Conclusions
Dans cet article, nous avons comparé deux approches algorithmiques («programmation dynamique» et «diviser pour mieux régner») pour résoudre des problèmes. Nous avons constaté que la programmation dynamique utilise le principe de «diviser pour mieux régner» et peut être appliquée à la résolution de problèmes si le problème contient des sous-problèmes entrecroisés et la sous-structure optimale (comme c'est le cas avec la distance de Levenshtein). La programmation dynamique utilise en outre des techniques de mémorisation et de tabulation pour préserver les sous-résolutions pour une réutilisation ultérieure.
J'espère que cet article a clarifié plutôt que compliqué la situation pour ceux d'entre vous qui essayaient de traiter des concepts aussi importants que la programmation dynamique et «diviser pour mieux régner» :)
Vous pouvez trouver plus d'exemples algorithmiques utilisant la programmation dynamique, avec des tests et des explications dans le référentiel
JavaScript Algorithms and Data Structures .
Codage réussi!