«C'est facile. Nous prenons la métrique de Schwarzschild, recherchons les symboles Christoffel, calculons leur dérivée, écrivons l'équation géodésique, modifions certaines coordonnées cartésiennes (afin de ne pas souffrir), obtenons une grande ODE multiligne - et résolvons-la. Quelque chose comme ça. "



Maintenant, il est clair que les trous noirs m'ont sucé. Ils sont infiniment fascinants. La dernière fois, j'ai compris comment visualiser la géométrie de Schwarzschild. J'ai été avalé par le problème d'une représentation précise de la façon dont la courbure d'un tel espace-temps affecte l'apparence du ciel (puisque les photons de sources éloignées se déplacent le long de lignes géodésiques incurvées par un trou noir) pour créer une simulation interactive. Voici le résultat (fonctionne dans le navigateur). L'astuce consiste à maximiser le calcul de la déviation des rayons lumineux. Tout fonctionne plus ou moins normalement, mais bien sûr, une telle simulation est loin d'être idéale, car en réalité aucun traçage n'y est effectué (pour les non-spécialistes: restauration de la localisation des rayons lumineux tombant dans le temps dans la caméra).

Mon nouveau projet corrige cette lacune en abandonnant l'efficacité / l'interactivité de la manière la plus simple possible: il s'agit d'un ray tracer purement sur le CPU . Le traçage est effectué aussi précisément et aussi longtemps que possible. Le rendu de l'image ci-dessus a pris 15 minutes (merci, RK4) sur mon ordinateur portable.

Il n'y a aucune amélioration par rapport à des travaux similaires. J'aime vraiment le faire. J'écris cet article pour partager non seulement les résultats, comme l'image ci-dessus (d' autant plus que d'autres ont fait mieux ), mais aussi le processus de création de ces images , avec une discussion / explication de la physique et de la mise en œuvre. Idéalement, cela peut inspirer ou devenir un guide pour les personnes ayant des intérêts similaires.

Recherchez de nouveaux rendus par le tag sans étoiles sur tumlr.

Un peu d'optique pseudo-Riemann

Ombre

Si vous avez déjà essayé mon applet , vous connaissez cette image:



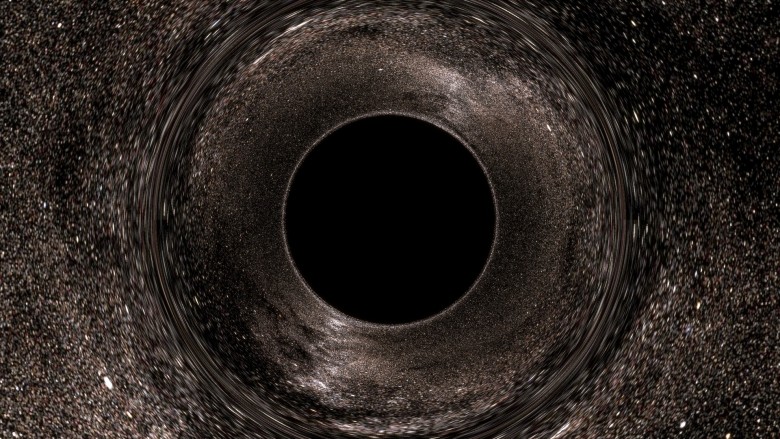
Il met en évidence les principales caractéristiques: un disque noir et un étrange anneau de distorsion.

Les discussions font souvent attention: il est faux de dire qu'un disque noir est un horizon d'événements. En fait, il est faux de dire que la zone d'image est un objet . Ceci est une image d'un objet. En effet, il existe des trajectoires qui, lors du suivi de votre œil à la source, apparaîtront dans l'horizon des événements (GS). Ce sont des pixels noirs, car aucun photon ne peut suivre ce chemin d'un trou noir (BH) jusqu'à votre œil. Ainsi, ce disque noir est très clairement une image de l'horizon des événements , en ce sens que si vous dessinez (dans un passé lointain) quelque chose directement au-dessus de l'horizon, les observateurs externes pourront le voir directement sur ce disque noir (nous exécuterons en fait cette expérience plus tard). Dans certaines publications, cette région noire est également appelée «l'ombre» de BH.



Cependant, il est intéressant de noter qu'il s'agit également d'une image de la sphère photonique (PS). Le graphique gnuplot en haut représente la géodésie des photons entrants depuis l'infini (en regardant le BH à distance lors du zoom) avec GS (noir) et FS (vert). Le rayon de la sphère de photons est 1,5 fois plus grand que le rayon de l'horizon des événements (dans la géométrie Schwarzschild) et ici les orbites circulaires des photons autour du trou noir sont autorisées (bien qu'instables). Sur le graphique, certains rayons tombent dans l'inexistence, tandis que d'autres sont dispersés (et apparaissent ainsi à un autre point de la sphère céleste). On peut voir que pour les rayons absorbés, le paramètre d'exposition est inférieur à ~ 2,5 rayons. C'est le rayon apparent du disque noir, et il est beaucoup plus grand que le GS et le FS.

Dans tous les cas, le fait suivant est important:

Un rayon lumineux incident librement dans la sphère de photons atteindra également l'horizon des événements.

Cela signifie que l'image de la sphère de photons est incluse dans l'image de l'horizon des événements. Mais comme le GS est clairement situé à l'intérieur du FS, l'image du premier devrait également être un sous-ensemble du second. Ensuite, les deux images doivent correspondre.

Pourquoi vérifions-nous que le disque noir est également une image du FS? Parce que cela signifie que le bord du disque noir est rempli de photons qui glissent le long de la sphère de photons. Le pixel immédiatement à l'extérieur du disque noir correspond à un photon qui (lors du traçage) tombe en spirale dans la sphère du photon, de plus en plus près d'une orbite circulaire instable, tournant plusieurs fois (plus vous regardez de près, plus il tourne rapidement), puis apparaît en spirale - puisque l'orbite est instable - et s'échappe à l'infini.

Ce comportement provoquera un effet optique intéressant similaire à la séparatrice dans un système dynamique. Théoriquement, si le faisceau est lancé exactement le long du bord, il tournera pour toujours en spirale, de plus en plus près de l'orbite circulaire de la sphère de photons.

Influence sur la sphère céleste

Nous ne nous concentrerons pas sur ce sujet, car la dernière applet lui est consacrée, et elle donne une bien meilleure idée des distorsions dans le ciel (y compris l'option de grille UV pour des distorsions plus nettes).

Juste quelques mots sur la bague Einstein. La lentille gravitationnelle se distingue optiquement car elle est l'image d'un seul point, qui est situé directement en face de l'observateur. L'anneau est formé à un tel angle de vision lorsque les rayons de l'observateur sont courbés en parallèle. Les rayons externes ne sont pas suffisamment courbés et restent divergents; à l'intérieur, ils se plient trop, convergent et peuvent en réalité même reculer ou tourner en cercle, comme nous l'avons vu.

Mais réfléchissez bien: si vous vous rapprochez suffisamment du disque noir, les rayons lumineux peuvent former un cercle, puis aller en parallèle. Là, nous devrions voir l'anneau secondaire d'Einstein. En fait, il peut y avoir des anneaux de n'importe quel ordre (n'importe quel nombre d'enroulements). Il devrait également y avoir des anneaux «étranges» entre eux, où les rayons de lumière se courbent en parallèle, mais sont dirigés vers le spectateur. Cette série interminable d'anneaux existe, mais elle est complètement invisible dans notre image (en fait, dans la plupart de ces images), car elle est trop proche du bord du disque.

Distorsion de l'horizon des événements

Quelque chose a changé dans cette nouvelle image. Tout d'abord, il est fait avec une meilleure résolution et avec un filtrage d'arrière-plan pour le rendre plus reconnaissable. Ensuite, j'ai zoomé sur l'image BH (sans s'approcher, nous sommes toujours à une distance de ~ 10 rayons de celle-ci, juste un zoom). Mais surtout, j'ai tracé une grille à l'horizon .

L'horizon n'est "qu'une sphère". Techniquement, ce n'est pas une sphère riemannienne standard avec une métrique spatiale. L'horizon est lumineux! C'est une façon colorée de dire qu'il se déplace à la vitesse de la lumière. Cependant, dans les coordonnées de Schwarzschild, c'est encore une surface $$$r = 1$ et nous pouvons utiliser $$$\ phi$ et $$$\ theta$ comme la longitude et la latitude. Ainsi, une grille peut être dessinée de manière canonique. Vous la voyez sur l'image.

La grille vous permet de voir un effet spécial qui peut être dérivé si nous analysons la courbe de diffusion / absorption des photons ci-dessus:

La surface entière de l'horizon est visible simultanément de n'importe quel point.

C'est très intéressant. Lorsque vous regardez une sphère fixe dans un espace-temps plat standard, vous ne voyez pas plus de 50% de sa surface à tout moment (si vous vous approchez, elle est inférieure à 50% en raison de la perspective). Mais l'horizon est visible en même temps qu'un disque noir: attention notamment aux pôles Nord et Sud. Néanmoins, bien que toute la surface soit placée sur un disque noir, elle ne le couvre pas entièrement : si vous zoomez sur le bord, vous verrez que l'image du GE se termine à la fin de l'ombre. Vous trouverez un anneau situé très près du bord extérieur, mais pas jusqu'au bout. Cette image est un point opposé à l'observateur et elle définit les limites de cette «première» image du HS à l'intérieur. Alors, qu'y a-t-il entre cet anneau et le bord réel? Je n'ai pas encore généré d'image agrandie, mais il existe une autre image entière de l'horizon des événements . Et puis un de plus, et un de plus, à l'infini. Il y a des images concentriques sans fin de tout l'horizon, compressées dans l'ombre. (Merci beaucoup / u / xXxDeAThANgEL99xXx pour avoir signalé ce phénomène que j'ai raté) .

Ajout d'un disque d'accrétion

Quel rendu moderne de BH fera sans disque d'accrétion? Bien que cette question soit clairement discutable, Nolan's Interstellar est-il vraiment disponible pour l'observation, sans parler de la précision, mais nous devons certainement remercier le blockbuster d'avoir popularisé une distorsion particulière du disque d'accrétion. Ici, nous avons un disque d'accrétion horizontal, infiniment mince, s'étendant de la sphère photonique (bien que cela soit très irréaliste car les orbites sont plus basses $$$3r_S$ instable, comme décrit ci-dessous) jusqu'à 4 rayons, peints dans une cage blanche et bleue. Avec une telle couleur, il est évident que nous sommes confrontés à un autre cas, alors qu'en même temps 100% de la surface de l'objet est visible.

Pour cette image, j'ai déplacé l'observateur un peu plus haut pour regarder le disque un peu d'en haut. Vous voyez des images de deux faces du disque : le haut et le bas. L'image se plie en arc au-dessus de l'ombre du trou noir car le faisceau dirigé directement au-dessus du trou noir se penche pour rencontrer la surface supérieure du disque derrière le trou, en face de l'observateur.

Cela explique également l'existence même de l'image inférieure: les rayons passant sous le BH sont courbés vers la surface inférieure du disque, qui se trouve derrière le BH. Si vous regardez attentivement, l'image se propage dans l'ombre, mais dans la partie supérieure, elle est beaucoup plus mince. Cela correspond aux rayons lumineux qui vont au-dessus du BH, font un cercle presque complet autour du trou et frappent la surface inférieure devant le disque.

Bien sûr, il est facile de conclure qu'il existe un nombre infini d'images de disques d'accrétion qui s'amincissent très rapidement lorsqu'ils approchent du bord. L'image suivante est déjà très mince, à peine visible dans la partie inférieure du bord.

Les GIF sont toujours pertinents

Dans cette animation convulsive, j'active / désactive la déviation de la lumière (anciennement Schwarzschild / Minkowski) pour clarifier certains des points dont nous avons parlé.





Ces deux gifs étranges sont créés à la demande des lecteurs. Dans le premier, l'observateur tourne autour d'un trou noir à une distance de 10 rayons. Cela ne doit pas être compris comme une orbite réelle, car en réalité il n'y a pas d'aberration lors du déplacement en orbite. Voici une série d'images BH fixes de plusieurs points où l'observateur se déplace d'un endroit à l'autre entre les images; c'est une orbite «adiabatique», si vous voulez.

Et la stéréo est toujours d'actualité

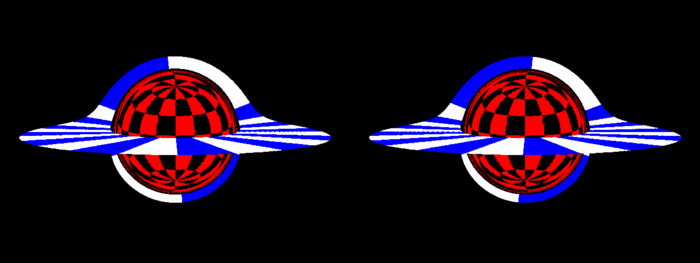
Fait intéressant, l'ombre semble assez plate.

Assez de science

Nous avons suffisamment d'images informatives dans le style des années 90 en basse résolution avec des couleurs vénéneuses. Voici quelques rendus «pop» (cliquez pour agrandir).


Cette image a été générée par l'utilisateur / n / dfzxh avec un suréchantillonnage quadruple


Plan plus grand


Image agrandie de l'anneau


L'effet culte de "l'anneau de lumière" vu du plan équatorial


Si vous téléchargez le programme, c'est la scène actuelle par défaut


Un lecteur beaucoup plus large

Eh bien, oui, rien de spécial. Il n'y a aucune illustration, juste des rendus du programme. Revenons temporairement à la science: la troisième image , qui semble n'avoir aucun sens, est en fait très précieuse. Il s'agit de la zone agrandie entre le bord supérieur du disque noir et l'image principale du disque d'accrétion. L'observateur se trouve sur le bord extérieur du disque d'accrétion lui-même et fait un zoom avant sur l'image. Le but était de représenter autant d'anneaux d'ordres différents que possible. Trois ordres sont visibles: la zone la plus claire dans la partie supérieure n'est que le bord inférieur de la première image de la surface extrême supérieure du disque. La barre ci-dessous, sous la mer calme d'étoiles étirées, est la partie supérieure de l'image de la face inférieure du disque. Tout en bas - une fine ligne de lumière d'une largeur ne dépassant pas un pixel, collée au disque noir de la sphère photonique. Il s'agit essentiellement de la troisième image: encore une fois, la surface supérieure distante, mais après que la lumière a terminé une révolution supplémentaire autour du trou noir. Fusionné avec lui, mais des images de plus en plus minces sont des anneaux d'un ordre supérieur. Eh bien, cela vaut également la balise <blockquote>:

Il existe des images sans fin des surfaces supérieure et inférieure du disque d'accrétion, et elles montrent toutes la surface entière du disque en même temps. De plus, à l'exception de la toute première, ces images ne passent ni devant le disque noir, ni devant l'autre, et sont donc «concentriques».

Magnifique.

J'accepte les demandes de rendu
Intéressé par une visualisation spécifique, mais pas prêt à passer par les difficultés d'installation du programme et de rendu vous-même? Envoyez-moi un reddit ou envoyez- moi un mail. Le rendu 1080p sur mon ordinateur portable ne prend pas plus de 10-20 minutes.

Disque d'accrétion réaliste

Le disque d'accrétion dans les rendus est assez cartoony. C'est juste un disque de texture stupide. Que se passe-t-il lorsque la physique réelle est incluse dans l'apparence visuelle d'un disque? Que se passe-t-il lorsque l'on considère le décalage vers le rouge par rapport au mouvement orbital, par exemple?

Un modèle populaire de disque d'accrétion est un disque de matière infiniment mince sur une orbite presque circulaire. Cela commence par l'ISCO (l'orbite circulaire la plus interne stable, $$$3r_s$ ) avec un profil de température selon une loi de puissance $$$(T \ sim r ^ {- a}$ . J'utiliserai une option très simple:

$$

$$T \ sim r ^ {- 3/4}$$

ce qui est définitivement anormal dans la théorie générale de la relativité pour les fluides réalistes, mais la voici (en tout cas, vous ne remarquerez pas la différence).

Maintenant, un paramètre libre est une échelle commune pour les températures, par exemple, la température en ISCO. Cette température est énorme pour la plupart des trous noirs. Nous parlons de centaines de millions de Kelvin; il est difficile d'imaginer un artefact humain qui pourrait exister sous l'influence du rayonnement du disque (pic de rayonnement X) à de telles températures, sans parler de la photographie. Nous devons donc clairement baisser la température. Évidemment, les trous noirs supermassifs sont plus froids, mais pas suffisants. Nous devons descendre à 10 000 K dans la CITP afin de pouvoir au moins voir quelque chose. C'est très inexact, mais c'est tout ce que je peux faire.

Il faut poser deux questions. Premièrement: de quelle couleur est le corps noir à cette température? Deuxièmement: quelle est sa luminosité ? Formellement, la réponse à ces deux questions se trouve dans le produit scalaire des fonctions décrivant les canaux R, G, B avec le spectre du corps noir. En pratique, certaines approximations sont utilisées.

Pour la formule de Tanner Helland , elle est précise et efficace pour la couleur, mais elle inclut de nombreuses conditions qui ne sont pas réalisables avec mon lancer de rayons (voir ci-dessous pour plus de détails). Le moyen le plus rapide est d'utiliser une texture simple:



Cette texture est l'une des nombreuses choses utiles dans la sélection de Mitchell Charity de "Quelle couleur est le corps noir?" . Pour référence, il correspond au point blanc E (point blanc E).

L'échelle montre la couleur d'un corps noir à des températures de 1000 K à 30 000 K, avec des températures plus élevées correspondant à peu près à la même nuance de bleu. Puisqu'il y a une énorme différence de luminosité entre les températures, cette texture ne peut pas et ne transmet pas la luminosité; il normalise plutôt les couleurs. Notre tâche consiste à calculer la luminosité relative et à l'appliquer. Une formule analytique convient pour cela. Si nous supposons que le spectre visible est très étroit, alors l'intensité visible totale est proportionnelle au spectre du corps noir lui-même:

$$

$$\ frac {1} {\ lambda ^ 5} \ frac {1} {\ exp (\ frac {hc} {\ lambda k_B T}) - 1}$$

où je me suis débarrassé des constantes stupides communes (nous allons toujours mettre à l'échelle la luminosité pour voir quelque chose). Vous pouvez simplement insérer $$$\ lambda$ approximativement pour la plage visible du spectre, et on obtient que la luminosité est proportionnelle à la température selon cette formule:

$$

$$(e ^ {\ frac {29622.4 \ text {K}} {T}} - 1) ^ {- 1}$$

C'est assez simple. À titre de vérification, nous notons que l'intensité relative tombe rapidement à zéro lorsque T s'approche de zéro et ne change pratiquement pas lorsque T passe à l'infini.

Redshift

Nous avons discuté des vitesses orbitales dans la géométrie de Schwarzschild dans la description de l'applet. Pour calculer le redshift, la formule de redshift du SRT est utilisée:

$$

$$(1 + z) _ \ text {Doppler} = \ frac {1 - \ beta \ cos (\ theta)} {\ sqrt {1- \ beta ^ 2}}$$

Où comme $$$\ cos (\ theta)$ - le cosinus de l'angle entre la direction du faisceau émis par le disque et la vitesse locale du disque, calculé dans le système de coordonnées inertielles locales de Schwarzschild. La formule est vraie dans ce contexte en raison du principe d'équivalence.

Il doit être multiplié par le coefficient de redshift gravitationnel:

$$

$$(1 + z) _ \ text {Gravitationnel} = (1 - r ^ {- 1}) ^ {- 1/2}$$

ce coefficient ne dépend pas de la trajectoire du faisceau lumineux, mais uniquement du rayon de rayonnement, car la géométrie de Schwarzschild est stationnaire.

Cela signifie également que la contribution de la position de l’observateur au décalage vers le rouge gravitationnel est constante sur l’ensemble du champ de vision. Notre image entière a un décalage bleu général constant, car nous sommes profondément en BH. Par conséquent, cet effet ne donne qu'une faible teinte qui peut être ignorée.

Nous négligeons également le décalage vers le rouge du mouvement de l'observateur, car notre observateur est stationnaire dans la géométrie de Schwarzschild. Voici le résultat final:



Comme vous pouvez le voir, la plupart du disque est entièrement blanc en raison de la luminosité maximale dans les canaux de couleur. Si vous abaissez ces canaux dans une plage de 0,0 à 1,0, les parties externes du disque deviennent pâles ou noires. L'augmentation de la luminosité est trop importante pour être vue et appréciée.J'ai essayé de montrer l'effet en utilisant le post-traitement afin que les parties les plus brillantes montrent une transition de couleur, mais ce n'est guère suffisant.

Image assez déroutante. Voici une image sans tenir compte de la luminosité, où vous pouvez évaluer les couleurs:



Ces images ont une résolution inférieure, car elles prennent beaucoup de temps à être rendues sur mon ordinateur portable (les racines carrées sont mauvaises, les enfants).

Dans tous les cas, ce rendu est mille fois moins spectaculaire que les autres (principalement parce que le bord intérieur du disque est déjà suffisamment éloigné du GS, donc la lentille est trop grande), mais le rendu est au moins précis . Si vous trouvez un trou noir avec une température de 10 000 K et de bonnes lunettes de soleil, vous le verrez.

Un autre gros plan. J'ai augmenté anormalement la saturation de la beauté:

Écrire un traceur de rayon de trou noir

Source Github

Il y a une différence très grande et évidente entre l'optique des trous noirs et l'intégrateur numérique, qui produit de beaux fonds d'écran avec une résolution de 1080p. La dernière fois, je n'ai pas publié mon raisonnement, mais j'ai simplement créé un référentiel git grand et sale. Maintenant, je veux expliquer un peu plus en détail, et essayer également de maintenir le code sous une forme plus précise et avec des commentaires.

Mon traceur n'a pas été créé bon, puissant, rapide. Tout d'abord, je voulais qu'il soit facile à mettre en place, à simplifier, afin que les gens puissent s'inspirer et voir le potentiel d'amélioration: même son imperfection peut inciter quelqu'un à décider d'écrire sa propre version. Voici un bref aperçu des algorithmes et de leur implémentation.

Potentiel "magique"

Donc, la théorie générale de la relativité, tout est clair. C'est simple. Nous prenons la métrique de Schwarzschild, recherchons les symboles Christoffel, calculons leur dérivée, notons l'équation géodésique, modifions certaines coordonnées cartésiennes pour éviter une souffrance sans fin, obtenons une énorme ODE multiligne, résolvez-la. Quelque chose comme ça.

Je plaisante. Bien sûr, il y a une astuce.

Si vous vous souvenez, la dernière fois que j'ai dérivé l'équation suivante pour l'orbite d'une particule sans masse dans son plan orbital dans la géométrie de Schwarzschild ($$u = 1 / r ):$u=1/r$

$$

$$u''(\phi) + u = \frac{3}{2} u^3$$

L'astuce consiste à voir la formule de Binet ici . Pour une masse d'une particule newtonienne dans le potentiel newtonien du champ des forces centrales:

$$

$$\frac{d^2}{dt^2} \vec x = \frac{1}{m} F(r)$$

alors la particule se déplacera évidemment dans son plan orbital et correspond à la formule de Binet pour $$$u(\phi)$ :

$$

$$u'' + u = - \frac{1}{m h^2 u^2} F(u)$$

O Where $$$\frac{d}{d\phi}$ Est un nombre premier $$$m$ - masse, et $$$h$- moment angulaire par unité de masse. C'est une équation pour l'orbite, pas une équation de mouvement. Cela ne dit rien$$$u(t)$ ou $$$phi(t)$ ne montre que la relation entre $$$u$ et $$$\phi$ .

Arrêtons-nous un instant pour réfléchir à ce que nous avons réellement obtenu. L'équation dit que si vous imaginez un système mécanique hypothétique d'une particule sous l'action d'une certaine force centrale, alors sa trajectoire sera une solution de la formule de Binet. Ensuite, le système mécanique devient un calculateur de formule.

C'est ce que je propose ici. Nous avons indiqué$$$m=1$ et ils ont pris (non physique, peu importe) un simple système d'une particule ponctuelle dans ce champ de force particulier:

$$

$$\vec F(r) = - \frac{3}{2} h^2 \frac{\hat r}{r^5}$$

où $$$h$Est une certaine constante, et résoudre l'équation numériquement est très simple. Alors la solution$$$\vec x (T)$ où $$$T$ - la coordonnée temporelle abstraite de ce système est, en fait, le paramétrage de la seule solution pour l'équation de Binet correspondante, qui est exactement l'équation géodésique .

Par conséquent, nous résolvons l'équation newtonienne en coordonnées cartésiennes, qui est généralement la plus simple (j'ai décidé d'utiliser la méthode Runge-Kutta pour permettre d'augmenter la taille des pas et de réduire le temps de rendu, mais à l'avenir l'utilisateur pourra choisir une méthode de solution différente). Ensuite, nous obtenons juste la géodésie réelle de la lumière, où $$$T$ Le paramètre va-t-il le long (contrairement à Schwarzschild $$$t$ , et du temps normal, qui n'existe pas).

C'est beaucoup mieux que la méthode précédente, qui fonctionnait avec des coordonnées polaires dans le plan orbital. Ici, les calculs sont très efficaces.

Ray tracing en numpy

Si vous regardez la source, vous verrez un script Python. Horreur! Pourquoi écrire le lancer de rayons en Python? Tout le monde sait à quel point les boucles s'exécutent lentement en Python, ce qui met toujours (presque) fin au travail. Le fait est que nous effectuons des calculs en numpy - et en parallèle. C'est pourquoi ce programme ne pourra pas afficher progressivement les parties déjà dessinées à l'écran: il restitue tout en même temps.

Tout d'abord, nous créons un tableau de conditions initiales. Par exemple, un tableau (numPixel, 3) avec des vecteurs pour tous les pixels de l'image (numPixel - largeur d'image × hauteur d'image). Ensuite, le calcul de chaque rayon est réduit à des tableaux de type (numPixel, ...) . Étant donné que les opérations avec des tableaux dans numpy sont très rapides et que tout est statiquement tapé ici (j'espère que je ne dis rien de stupide pour le moment), cela devrait être calculé assez rapidement. Ce n'est peut-être pas C, mais toujours rapide. En même temps, nous avons la flexibilité et la clarté de Python.

Cette méthode est terrible pour le lancer de rayons standard, où les objets ont des parties diffuses, réfléchissantes et réfractantes et il est important de considérer les conditions d'éclairage. Par exemple, la réflexion sélective de parties d'un réseau de rayons est un véritable cauchemar; le suivi des valeurs booléennes ou des indices de boucle nécessite plusieurs masques et les boucles ne peuvent pas être rompues. Mais voici un autre cas: tous les objets de notre scène n'émettent que de la lumière: le ciel, un disque d'accrétion chaud, un horizon d'événements noir comme du noir et de la poussière brillante. Ils ne sont pas affectés par la lumière incidente, et la lumière elle-même les traverse également calmement, sauf pour réduire l'intensité. Cela nous amène à un algorithme pour déterminer la couleur:

Mélange de couleurs

C'est simple: il vous suffit de mélanger tous les objets entre nous et la source de rayons avec leurs valeurs alpha correspondantes, et de les placer les uns sur les autres, là où les plus éloignés seront en bas. Nous initialisons le tampon de couleur avec du noir alpha-transparent, puis lorsque nous entrecoupons avec l'objet, nous mettons à jour le tampon en mélangeant la couleur de l'objet sous notre tampon de couleur. Nous effectuons les mêmes étapes pour la poussière (utilisez le profil de densité $$$r ^ {- 2}$ ) et continuer à parcourir jusqu'à la fin. Notez que le canal alpha fonctionne également comme un tampon Z, car l'objet cesse de contribuer après que le rayon a traversé l'objet opaque (ce qui définit ainsi la valeur alpha du tampon à 1,0).

L'inconvénient évident de cette méthode est que vous ne pouvez pas arrêter le lancer de rayons après l'avoir calculé, car elle fait partie du réseau où se poursuit le suivi d'autres rayons. Par exemple, après une collision avec l'horizon, les rayons continuent à errer au hasard après être tombés dans une singularité - vous pouvez voir ce qui se passe si vous désactivez explicitement l'objet horizon. L'algorithme de fusion alpha garantit qu'ils n'affectent pas l'image finale, mais ces rayons chargent toujours le processeur.