Je continue de familiariser les lecteurs de Habr avec les chapitres de son livre "Theory of Happiness" avec le sous-titre "Mathematical Foundations of the Laws of Meanness". Ce livre de science populaire n'est pas encore publié, racontant de manière très informelle comment les mathématiques vous permettent de regarder le monde et la vie des gens avec un nouveau degré de conscience. C'est pour ceux qui s'intéressent à la science et pour ceux qui s'intéressent à la vie. Et puisque notre vie est complexe et, dans l'ensemble, imprévisible, l'accent dans le livre est principalement sur la théorie des probabilités et les statistiques mathématiques. Ici les théorèmes ne sont pas prouvés et les fondements de la science ne sont pas donnés, ce n'est en aucun cas un manuel, mais ce qu'on appelle la science récréative. Mais c'est précisément une approche si ludique qui nous permet de développer l'intuition, d'égayer les cours pour les étudiants avec des exemples vivants et, enfin, d'expliquer aux non-mathématiciens et à nos enfants que nous avons trouvé des choses si intéressantes dans notre science sèche.Dans ce chapitre, nous discuterons de l'argent, des marchés et de l'entropie, et nous examinerons également les gifs animés, qui, hélas, ne peuvent pas être imprimés dans un livre.
Observation de Hongren:
Chez les économistes, le monde réel est souvent considéré comme un cas particulier.
L'économie est une science importante, sérieuse mais particulière. Sans aucun doute, elle est d'une nécessité vitale en tant que discipline qui étudie le phénomène réel et important de notre monde: la réalité économique. La science économique vise la prouvabilité et la formalisation, elle a beaucoup de mathématiques, parfois complexes et intéressantes. Cependant, en ouvrant un manuel économique sérieux, vous trouverez très probablement des calculs relativement simples, des recettes toutes faites et un tas de raisonnements informels dans cet esprit: «mais en fait, tout peut être faux et, en général, comme vous le souhaitez, si cela se produit la volonté des principaux acteurs ou du gouvernement. » En fin de compte, on peut avoir le sentiment que l'intuition, la connaissance de la psychologie et la capacité de percevoir le contexte général sont plus importants dans cette discipline qu'un calcul précis et un examen méticuleux des détails (il s'agit d'économie, pas de comptabilité). Enfin, près de la moitié des fausses thèses sont écrites spécifiquement sur l'économie; il n'est donc pas si difficile de raisonnablement argumenter sur des sujets économiques. Nous allons également essayer notre force dans ce domaine, bon, nulle part l'injustice de ce monde n'est plus aiguë que dans la question de la répartition des richesses. De plus, peu importe ce qu'une personne fait, quelle que soit la profession qu'elle possède, elle est impliquée dans l'économie et ses jeux, des lois de l'économie, ainsi que des lois de la physique, à ne pas cacher.
Sur l'ensemble des problèmes résolus par l'économie mathématique, nous n'en considérerons qu'un - comment il s'avère que même dans des conditions égales pour tous les acteurs du marché et un échange équitable de fonds, les pauvres deviennent plus riches que les riches et pourquoi même une société mathématique idéale est sujette aux inégalités financières. Eh bien, en cours de route, nous apprenons quelque chose d'intéressant sur les statistiques mathématiques et les distributions de variables aléatoires.
Je suis physicien de formation et de profession, et ma déformation professionnelle s'exprime dans une vision particulière du monde, comme dans une variété de systèmes et de processus physiques différents. Du point de vue d'un physicien, le marché réel est un système ouvert sensiblement non stationnaire, avec de nombreux degrés de liberté, dans lequel les processus stochastiques (aléatoires) jouent un rôle important. En ce sens, le marché est similaire au sujet de l'étude de branches de la physique comme la thermodynamique et la physique statistique, dans lesquelles, compte tenu de l'impossibilité de considérer tous les innombrables détails et le comportement de toutes les composantes du système, ils passent à des propriétés généralisantes et mesurables, telles que l'énergie, la température ou la pression . Il n'est pas surprenant que des tentatives de description thermodynamique des systèmes économiques et de création d'éconophysique aient été entreprises depuis plus de cent ans. Mais le problème est: alors que les scientifiques examinent les détails, résument les connaissances acquises et discutent des lois fondamentales, l'objet principal de l'étude est la réalité économique et a le temps de changer au-delà de la reconnaissance. Son comportement semble chercher à préserver, voire à accroître son incertitude et son imprévisibilité.
Un bon exemple est l'histoire de deux siècles de l'utilisation de l'analyse technique lorsque vous jouez en bourse. Lorsqu'un nouvel outil puissant apparaît qui vous permet de chercher des modèles cachés et de prédire le prix d'un titre ou d'un titre, il commence à faire des bénéfices pour ceux qui l'utilisent. Mais bientôt le marché commence à «sentir» de nouveaux acteurs et à s'adapter à leur stratégie, la précision des prédictions de la merveilleuse méthode commence à chuter et, après un certain temps, elle tombe dans une grande liste d'outils obsolètes et peu fiables. Ni les algorithmes modernes et flexibles de réseaux neuronaux à apprentissage automatique, ni les traders de robots ultra-rapides effectuant des millions d'opérations par minute n'ont changé la propriété principale du jeu de la bourse au cours des deux dernières décennies - son imprévisibilité. Et jusqu'à présent, les principaux avantages d'un professionnel dans cette industrie sont la volonté, l'endurance de caractère, l'aversion pour la passion ... enfin, ou la propriété de l'échange. Tout est comme dans un casino où les jeux sont basés sur le pur hasard! D'une part, cela est bien sûr insultant et, d'autre part, cela donne l'occasion d'améliorer constamment les méthodes et les approches. Il était une fois la théorie des probabilités et les statistiques mathématiques nées de tentatives d'analyse des jeux de hasard et des jeux économiques, et ce n'est qu'alors qu'elles ont trouvé une application dans presque toutes les sciences naturelles.
Dans une discussion plus approfondie, nous parlerons d'argent, mais cette catégorie habituelle utilisée quotidiennement est étonnamment complexe et ambiguë. La signification et la valeur de l'argent dépendent de nombreux facteurs, et hors contexte appelant une certaine somme d'argent, nous ne disons rien de sa valeur réelle. Cela distingue les valeurs monétaires de la plupart des quantités physiques qui décrivent notre monde et rend difficile la conduite de discussions rigoureuses dans l'économie. Mais le but de notre conversation: les fondements mathématiques des lois de la méchanceté, au quotidien, compréhensibles et simples. Par conséquent, à l'avenir, nous parlerons de "roubles", se référant à un billet ou à une pièce de monnaie formel, et impliquant que plus ces "roubles" ont, plus ils sont riches. D'autres discussions sur le pouvoir d'achat, les valeurs intangibles ou non liquides, et «le bonheur n'est pas en argent», enfin, nous laisserons de côté la conversation.
Allez, arrête!
Nous commençons par analyser la justice de quelques stratégies simples pour distribuer une certaine somme d'argent à un groupe fini de personnes.
La première stratégie, la plus évidente: «tout prendre et diviser», c'est-à-dire donner à chaque membre du groupe une part égale du montant total. Une telle distribution est appelée
dégénérée , elle a un indice de Gini égal à zéro et correspond à une courbe d'égalité dans le diagramme de Lorentz.
Répartition dégénérée de l'argent absolument équitable: tout le monde est divisé également.Excellente option! Nous l’appellerons
«stratégie de Sharikov» en l’honneur du héros de l’histoire de Mikhaïl Boulgakov «Dog Heart», qui proposait ainsi de résoudre tous les problèmes économiques.
La deuxième stratégie, plus réaliste, consiste à distribuer à tout le monde un rouble au hasard. Qui a de la chance. Nous pouvons appeler cette stratégie
«Poisson» , car c'est ainsi que les événements aléatoires indépendants du processus de Poisson sont distribués sur l'échelle de temps. Pour un groupe de
n personne la probabilité que chacun des participants reçoive le rouble est

. Après la distribution de cette façon
M roubles, chacun devrait recevoir un montant égal au nombre de ces résultats "positifs". La fonction de probabilité pour une telle somme est bien connue - il s'agit d'une
distribution binomiale , semblable à une cloche, diffusant symétriquement autour de la valeur moyenne
M / n . Habituellement, ils le lui présentent en calculant la probabilité d'obtenir le montant indiqué en lançant des dés. Pour les grandes valeurs
M la distribution binomiale devient presque impossible à distinguer de la normale. Voyons comment cela va changer, comme l'argent est distribué, la distribution de l'argent dans le groupe et son équité.
Le résultat de la distribution d'argent sur le principe de "qui Dieu enverra" est une distribution binomiale. Plus nous donnons d'argent, plus la valeur de la moyenne et de l'écart est grande, mais la probabilité de ne rien obtenir disparaît presque.Algorithme de stratégie de PoissonDonnées initiales : xs - un tableau de n éléments remplis de zéros, M - le montant total d'argent dans le système.
M i <- 1 n xs[i] <- xs[i] + 1
Cette distribution, du point de vue de la justice, a l'air très bonne, d'ailleurs, elle devient d'autant plus équitable que l'on donne plus d'argent au public! Tout simplement génial! Il est dommage que la société ne soit pas organisée de la même manière et que la pluie ne se déverse pas sur nous tous également.
Pour compléter le tableau, regardons une autre distribution artificielle simple de l'argent -
uniforme . Avec cette répartition des pauvres seront autant que les riches.
Même une distribution ne signifie pas que l'argent est réparti uniformément entre tous. Avec cette distribution, le nombre de paysans riches, pauvres et moyens est le même, mais l'argent appartient principalement aux riches.Algorithme de stratégie de distribution uniformeDonnées initiales : xs - un tableau de n éléments remplis de zéros, M - le montant total d'argent dans le système.
x xs x <- 0 M/n
Pour une distribution uniforme, la courbe de Lorentz est une parabole quadratique, et si la frontière gauche de la distribution est nulle, alors cette parabole est indépendante de la position de la frontière droite, et l'indice de Gini pour toutes ces distributions est exactement
1 / 3 . Une telle valeur d'indice (mais pas une telle distribution!) Était, par exemple, dans l'économie australienne dans les années 2000 - c'est un assez bon indicateur.
Cependant, le marché est le marché! Les distributions considérées ci-dessus sont bonnes, mais nécessitent des conditions spéciales pour leur apparition. Si vous donnez aux gens la liberté d'échanger de l'argent, de changer de l'argent pour des services, de l'enregistrer et de le dépenser en une nuit, les distributions idéales perdront leur stabilité et se transformeront en d'autres.
Nouvelle politique économique!
Considérez un groupe de
n la personne. À la suite de la révolution, nous distribuerons à tous les participants à l'expérience une somme d'argent égale - pour
m roubles à tout le monde, ayant reçu la répartition la plus équitable des fonds Sharikov dans la société. Nous allons maintenant leur donner la liberté de s'enrichir et d'appauvrir par la volonté de leur propre destin et de construire un modèle de marché primitif. Nous demandons à quelqu'un choisi au hasard de donner un rouble à toute personne du groupe qui a également été choisie au hasard. Disons qu'il s'agit de l'achat d'un certain service à un prix fixe. La répartition des richesses devrait changer: quelqu'un aura moins d'argent, quelqu'un de plus. Répétons la procédure d'échange encore et encore et examinons comment la répartition des richesses dans le groupe va changer.
Il est prudent de réfléchir à ce que nous attendons de voir avant de mener l'expérience. L'échange d'argent entre les participants se produit tout aussi vraisemblablement, comme dans le cas de la stratégie de Poisson de distribution d'argent, mais en même temps, les joueurs perdent de l'argent, d'ailleurs, selon le même principe de Poisson et avec la même intensité. Ainsi, on peut supposer que les incréments positifs et négatifs seront normalement distribués et situés symétriquement par rapport à zéro. Chaque joueur, à la fin, recevra une différence de ces incréments, qui pour deux variables aléatoires normalement distribuées seront également normalement distribuées, dans ce cas, autour de zéro, car les pertes et les gains sont symétriques.
Après de nombreux échanges, chaque joueur recevra et perdra un montant qui obéit à une distribution proche de la normale. Le revenu total sera également normalement distribué autour de zéro.Ainsi, nous obtenons une marche aléatoire classique avec des incréments normalement distribués et pouvons nous attendre à une certaine diffusion des fonds autour de la moyenne
m . La fonction de probabilité doit être floue, augmentant la variance à une valeur moyenne constante. Tout semble simple.
Mais il y a une nuance. Si, pour une raison quelconque, quelqu'un du groupe n'a plus de fonds, il ne pourra pas acheter de services en donnant de l'argent, mais, en même temps, il pourra le recevoir. La valeur possible de la richesse est limitée à zéro à gauche, ce qui signifie que la diffusion de la richesse ne peut pas s'étendre indéfiniment, et la fonction de probabilité observée, tôt ou tard, cessera d'être symétrique.
Il y a encore une nuance. Le montant d'argent dans notre système fermé est limité et invariable, ce qui signifie que les promenades aléatoires ne sont pas indépendantes. Un joueur chanceux pourra obtenir de très grandes quantités et s'éloigner de l'ensemble, mais seulement si la masse totale devient plus pauvre. Les participants à l'expérience sont réunis par un réseau invisible par la loi de l'économie d'argent dans le système. À quoi s'efforcera la distribution de l'argent dans ces conditions? Il semble que la réponse ne soit pas aussi évidente qu'elle pourrait l'être à première vue, passons à la simulation et voyons ce qui se passe.
Résultat de la simulation pour partager une somme d'argent égale n = 1000 et m = 100 . Au début, en effet, un phénomène similaire à la diffusion est observé, mais comme la fonction de probabilité atteint la frontière gauche, la distribution tend vers une forme asymétrique caractéristique et pas très juste avec un coefficient de Gini proche de  .
.Algorithme de quantité égaleDonnées initiales : xs - un tableau de n éléments, initialisé avec m valeurs.
i <- 0 n xs[i] > 0 j <- 0 n xs[i] <- xs[i] - 1 xs[j] <- xs[j] + 1
Si un physicien lit ce livre, il pourra supposer avec confiance qu'il pourrait s'agir d'une distribution; il l'appellera la distribution de Gibbs. Un lecteur attentif se souviendra peut-être que nous avons déjà rencontré une image similaire et un tel indice de Gini lorsque nous avons examiné la frustration en attendant un bus. Nous avons ensuite examiné la distribution des intervalles entre les événements de Poisson, qui a été décrite par une distribution exponentielle. Ces deux messieurs avisés auront raison, appelant des noms différents la même merveilleuse distribution.
Les gens sont des molécules
La distribution de Gibbs provient du domaine de la physique statistique. Il décrit les propriétés de systèmes appelés le beau mot "ensemble", qui se composent d'un grand nombre d'éléments en interaction, le plus souvent des particules. Dans l'ensemble, vous pouvez sélectionner des sous-systèmes arbitraires (par exemple, des particules individuelles ou leurs groupes) et leur attribuer certaines fonctions d'état (il peut s'agir de coordonnées généralisées, de vitesses, de concentrations, de potentiels chimiques, etc.). En utilisant les méthodes de la physique statistique, il est possible d'expliquer et de calculer les paramètres d'une grande variété de phénomènes: processus chimiques et catalytiques, turbulence, ferromagnétisme, comportement des cristaux liquides, superfluidité et supraconductivité, et bien d'autres.
La distribution de Gibbs répond à la question: quelle est la probabilité de rencontrer un certain état du sous-système si a) l'énergie d'état est donnée, b) les propriétés macroscopiques (relativement parlant, globales) du système, telles que la température, et c) sait-on que le système est en équilibre thermodynamique? Il peut être schématiquement exprimé comme suit:
p m a t h r m G i b b s ( T ) ( x ) = C e - f r a c E ( x ) k T ,
où
x - un certain état du sous-système,
E ( x ) Est l'énergie de cet état,
T Est la température absolue du système (ou de son analogue), et
C et
k - valeurs nécessaires à la normalisation et à la conformité des dimensions. La condition d'équilibre est très importante, cela signifie que le temps disparaît de la considération et que l'ensemble du système sera dans son état le plus probable pour les conditions données.
Nous n'avons pas besoin d'une dérivation rigoureuse de l'expression pour la distribution de Gibbs ici; au lieu de cela, je veux montrer un beau raisonnement purement mathématique qui mène à sa forme exponentielle. Puisque nous considérons les parties du système qui s'additionnent à l'ensemble du système, il vaut la peine de choisir une quantité
additive comme caractéristique, c'est-à-dire que sa valeur pour l'ensemble est la somme arithmétique des valeurs de ses parties. L'énergie peut être utilisée en tant que telle quantité en mécanique. D'autre part, nous calculons la probabilité d'observer un certain état du système, et la probabilité est
multiplicative , c'est-à-dire que si le système peut être divisé en parties, alors la probabilité d'observer toutes ces parties en même temps sera égale au produit des probabilités pour l'état de chacune des parties. Ainsi, nous avons besoin d'une fonction qui transforme une quantité additive en une quantité multiplicative. Seule la fonction exponentielle a cette propriété.
un x , la somme des arguments se transforme en un produit de valeurs:
a x + y = a x a y . Eh bien, de toutes les fonctions exponentielles, la plus pratique est l'exposant, car il se comporte très bien lorsqu'il est intégré et différencié.
Dans notre modèle de marché, nous avons une quantité additive - la quantité d'argent que possède chaque joueur, c'est un analogue de l'énergie. Dans l'échange décrit par nous, cette quantité, comme l'énergie dans le système physique, est conservée. Et quel est le point de la température? Il est facile de le découvrir en regardant l'expression de la densité de probabilité de la distribution exponentielle:
p mathrmExp( lambda)(x)= lambdae− lambdax,
et en se rappelant que la moyenne pour lui est
1/ lambda . Étant donné que le nombre de joueurs pendant le processus d'appel d'offres est inchangé, le montant moyen arithmétique de l'argent des joueurs est égal au montant initialement distribué.
m . Il s'ensuit naturellement que
lambda=1/m , alors le montant moyen d'argent des joueurs agit comme la température dans notre modèle économique. Sur un marché «réchauffé» avec une grande liquidité, on pourra observer une plus grande dispersion du niveau de bien-être que sur un «froid», car la dispersion dans la distribution exponentielle est
1/ lambda2 . Comme l'a déclaré Ostap Bender dans le «Veau d'or» de I. Ilf et E. Petrov: «Une fois que certains billets de banque errent dans le pays, il doit y avoir des gens qui en ont beaucoup.»
Pour être absolument précis, et rappeler que l'argent dans notre expérience est une quantité discrète, alors nous observons une distribution
géométrique - un analogue discret d'exponentielle. Cela se produit dans le problème du comptage du nombre d'échecs avant la première victoire lors du lancement de pièces de divers degrés d'honnêteté. Ces deux distributions sont similaires et deviennent indiscernables avec une diminution de la probabilité de gagner. Dans notre expérience, les chances d'obtenir le rouble sont égales

, il est suffisamment petit pour appeler l'exponentielle de distribution.
Reste à faire face à l'équilibre de l'état final du marché. L'équilibre thermodynamique peut être décrit de différentes manières. Premièrement, l'état
stationnaire doit être en
équilibre , dans lequel le système peut rester indéfiniment, sans changer ses paramètres macroscopiques, et sans former à l'intérieur de lui-même des flux ordonnés de matière et d'énergie. Deuxièmement, il doit être
stable , c'est-à-dire que si le système est déséquilibré, il aura tendance à y revenir. Troisièmement, il s'agit de l'état le plus probable du système, le plus souvent observé, dans lequel, au fil du temps, le système aura tendance à passer de tout autre état hors équilibre. Notre expérience démontre ces critères d'équilibre: étant arrivé à une distribution exponentielle, le système y reste, et d'ailleurs, il est facile de s'assurer dans l'expérience que de toute distribution arbitraire, après un certain temps, nous arrivons à nouveau à exponentielle. Mais ce n'est pas une preuve, mais seulement un indice que nous avons très probablement affaire à l'équilibre. Nous avons besoin d'une sorte de critère formel mesurable qui nous indiquerait sans ambiguïté que le système est en équilibre sans avoir besoin d'attendre indéfiniment ou de trier toutes les distributions initiales possibles. Ce serait un critère utile qui pourrait être appliqué au marché réel, sans qu'il soit nécessaire de mener des expériences risquées sur des personnes vivantes.
Tao exprimé en mots - pas vrai Tao
Les réflexions sur l'équilibre ont conduit les physiciens au concept d'
entropie , qui est progressivement allé au-delà de la thermodynamique et a été si apprécié par les scientifiques de toutes les directions, les philosophes et le grand public, que l'entropie a maintenant reçu une aura de mystère, d'incompréhensibilité et Dieu sait autre chose. Un concept simple et spécial, par essence, a acquis une réputation dans l'esprit des masses en tant que concept gouvernant inexplicablement le monde. Cela est dû au fait que la thermodynamique est une science universelle qui décrit à un niveau d'abstraction très élevé un système de nature très diverse: du physique, chimique et biologique au social, économique et même purement humanitaire. Après le cours, cependant, il reste le sentiment que la thermodynamique concerne un gaz idéal ennuyeux, des pistons et un cycle de Carnot impossible. Une telle vision très unilatérale est liée au fait remarquable que la thermodynamique, étant l'une des branches les plus abstraites et universelles des sciences naturelles, résout avec élégance les problèmes appliqués qui sont compréhensibles pour les écoliers et utiles dans l'industrie. Cela ne peut pas être dit, par exemple, à propos de la théorie des catégories ou de la topologie, qui sont également des disciplines très abstraites, universelles et sans aucun doute utiles, mais elles ne sont presque jamais rencontrées dans les tâches quotidiennes.
Alors entropie. Le créateur de la thermodynamique, Clausius, et plus tard Gibbs et Boltzmann, a exigé une caractéristique quantitative d'équilibre, indiquant la probabilité d'observer l'état indiqué du système ou de ses parties. De plus, cette valeur, qui reflète une probabilité de nature multiplicative, doit être une fonction d'état additive pour pouvoir être calculée pour le système en additionnant les valeurs calculées pour ses parties. Lorsque nous avons cherché une fonction appropriée pour la distribution de Gibbs, nous sommes partis du fait qu'elle devrait transformer un argument additif en une valeur multiplicative. Lors de la recherche d'une expression pour l'entropie, nous avons besoin d'une fonction qui est multiplicative en argument et additive en valeur - c'est une fonction logarithmique, l'inverse de l'exponentielle. L'entropie de l'état d'un système complexe peut être exprimée comme la valeur attendue pour le logarithme de la probabilité d'observer l'état de toutes ses parties, ou, selon Boltzmann, comme le logarithme du nombre de façons dont cet état du système peut être réalisé. Dans ce cas, l'état le plus probable correspond à une valeur d'entropie plus grande, et à l'état d'équilibre, le maximum possible.
Le nombre de façons de réaliser tel ou tel état dépend du nombre de restrictions ou de conditions dans lesquelles cet état peut être réalisé. Moins il y a de telles restrictions, plus l'état est probable et plus la valeur de son entropie est élevée. Ces restrictions et conditions donnent un sens aux
informations de statut. D'où l'idée que l'entropie reflète le degré de notre ignorance du système: moins nous en savons sur l'état, plus son entropie est grande. Shannon a généralisé plus tard ce concept pour tous les systèmes contenant des informations, y compris pour les distributions de variables aléatoires. Voici ce qu'il a fait: pour une variable aléatoire
X défini par une fonction de probabilité
p(x) l'entropie est définie comme suit:
H(X) equiv− mathrmM( ln(p(x)))=− sump(x) ln(p(x)),
où la sommation est effectuée sur toutes les valeurs
x dans lequel
p(x)>0 . Ainsi, nous sommes capables de calculer l'entropie de l'état de tout système complexe, ayant sa description statistique.
C'est ainsi que l'entropie change à mesure que notre modèle de marché arrive à l'équilibre.
La croissance de l'entropie à mesure que le marché se rapproche de l'état d'équilibre. La ligne horizontale sur le graphique de droite montre la valeur théorique de l'entropie pour la distribution exponentielle, égale à 1− ln( lambda) . Le «plateau» intermédiaire correspond à la période pendant laquelle la distribution a traversé l'étape de diffusion et a semblé normale.Ainsi, chaque distribution: définie analytiquement ou obtenue expérimentalement sous forme d'histogramme, peut être associée à un nombre positif - son entropie. Cela signifie que les distributions peuvent être comparées entre elles, déterminant plus ou moins l'équilibre et probable pour des conditions données. De plus, pour une certaine classe de distributions, il est possible de distinguer une distribution à entropie maximale, d'ailleurs, une seule. Les classes sont définies par des contraintes, ou la mesure de notre connaissance des propriétés statistiques d'un système. Voici quelques exemples:
| que savons-nous de la variable aléatoire X | distributions avec entropie maximale |
|---|
| X i n [ a , b ] | uniforme sur la coupe [ a , b ] |
| X \ in \ {0,1 \} | Distribution Bernoulli |
| X in[0, infty) + moyenne | exponentielle, pour une quantité discrète - géométrique |
| X in[xm, infty) + moyenne géométrique | Distribution de Pareto (pouvoir) |
| X in[0, infty) + moyenne + moyenne géométrique | distribution gamma |
| X in[0, infty) + moyenne géométrique + variance pour la moyenne géométrique | log normal |
| X in(− infty, infty) + moyenne + variance | normal |
Familier tous les visages! Ce sont des distributions très souvent utilisées que les statisticiens appliquent à la classe de tâches la plus large. Leur universalité est précisément due au fait que, ayant une entropie maximale, ils sont les plus probables et observables. Pour eux, comme l'équilibre, de nombreuses distributions de variables aléatoires réelles ont tendance. La distribution la plus libre de toutes restrictions est la distribution normale: elle nécessite un minimum d'informations sur une variable aléatoire. Moins échouera: si nous n'indiquons que la valeur moyenne, alors dans un effort pour augmenter l'entropie, la distribution «s'étalera» sur tout l'axe numérique.
Mais, si nous ne connaissons que la valeur moyenne, mais en même temps limitons la variable aléatoire à des valeurs positives, alors la distribution d'équilibre sera sans ambiguïté - exponentielle. C'est ce cas que nous avons observé dans notre expérience avec le marché. Nous ne savions à l'avance que le montant que nous donnions à chaque joueur et le fait que le montant d'argent dans le système était constant, cela fixait une valeur moyenne. Et puisque notre argent est positif, très probablement, en équilibre, nous obtenons la distribution exponentielle de la richesse avec l'indice de Gini égal à1/2 .
Il existe de nombreuses modifications du modèle que nous décrivons: l'échange peut avoir lieu non pas dans un rouble, mais dans une valeur aléatoire limitée par l'état du donateur, alors qu'il est possible de donner de l'argent non à un seul joueur, mais à le distribuer au hasard. Jusqu'à ce que nous introduisions de nouveaux paramètres dans le jeu, toutes ces modifications ne changent pas la forme de la distribution d'équilibre de la richesse - elle reste exponentielle. Vous pouvez le vérifier à l'aide de la simulation, mais ce n'est pas intéressant de donner des images pour différentes méthodes d'échange - elles sont toutes les mêmes. De nombreux chercheurs ont noté cette caractéristique des modèles de marché. Un modèle intéressant est celui construit par Dragulescu et Yakovenko de l'Université du Maryland, dans lequel les joueurs sont combinés dans certaines entreprises, puis l'interaction des entreprises avec les joueurs-travailleurs et les joueurs-acheteurs est simulée.Mais même dans ce cas complexe, l'équilibre est la distribution exponentielle, qui est indifférente aux paramètres choisis du modèle.Pour démontrer l'universalité du principe de l'entropie maximale, limitons artificiellement le niveau de richesse d'un joueur individuel d'en haut, en lui interdisant de recevoir de l'argent s'il dispose déjà d'un certain montant fixe. La distribution d'équilibre, bien sûr, va changer. Et dans le cas où la bordure droite est égale à deux fois la valeur moyenne, alors nous arrivons au cas décrit dans la première ligne du tableau. En effet, en limitant la variable aléatoire à un segment fini et en n'indiquant rien d'autre, nous ne pouvons supposer aucune autre valeur attendue de la moyenne, à l'exception du milieu de ce segment. Par conséquent, la distribution d'équilibre avec cette option doit être uniforme. Vérifions si c'est le cas?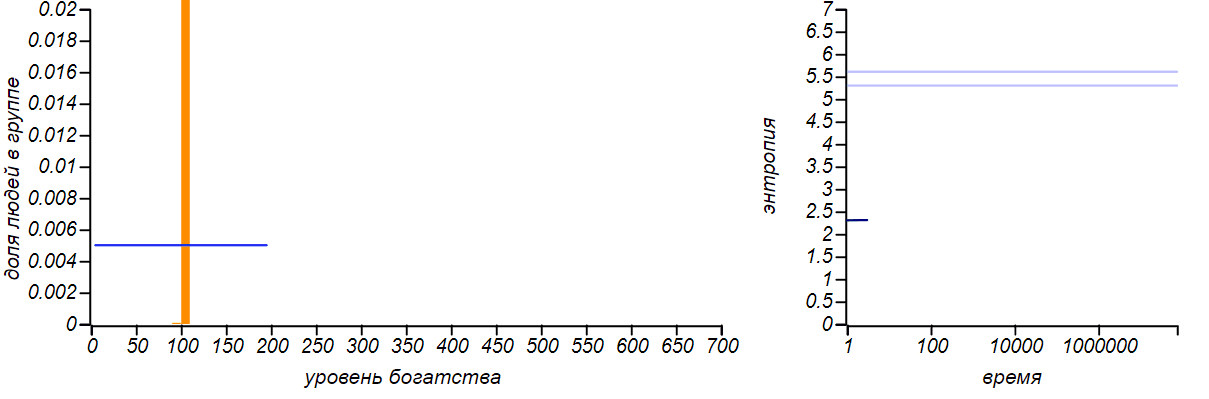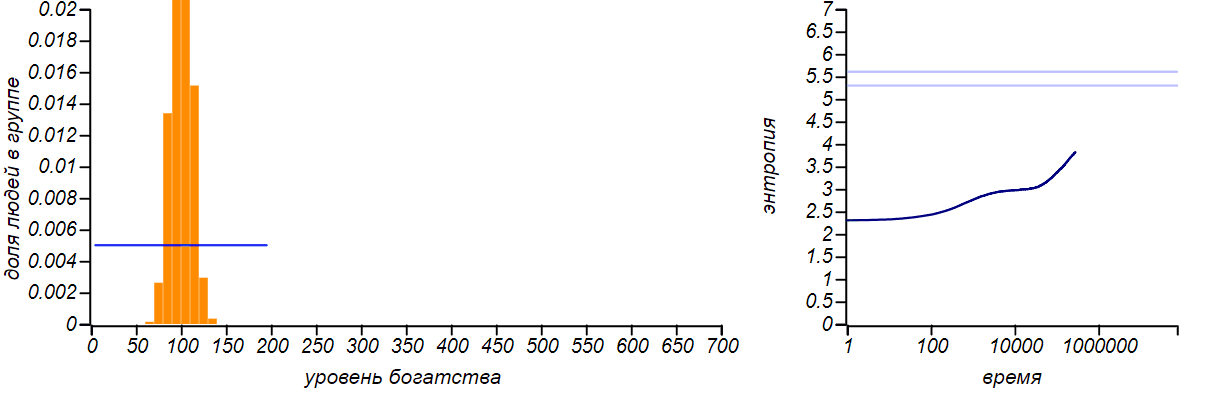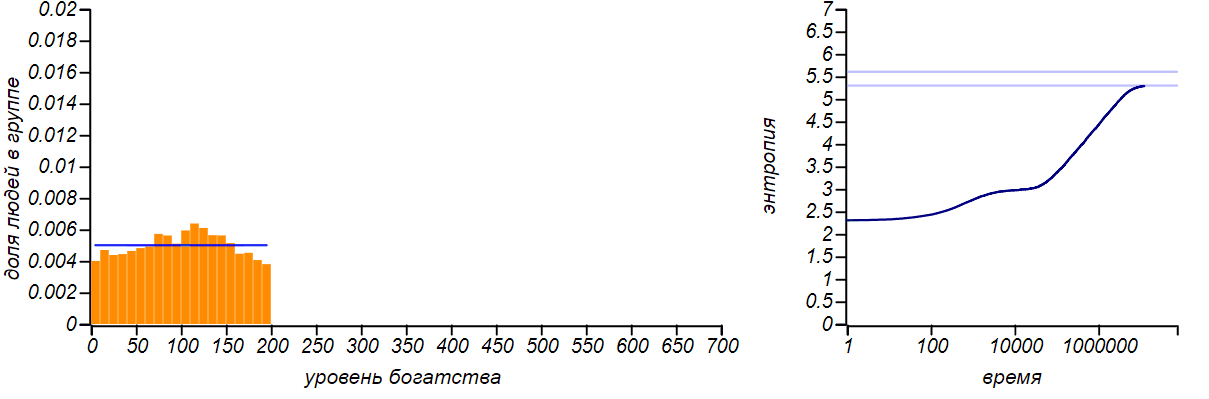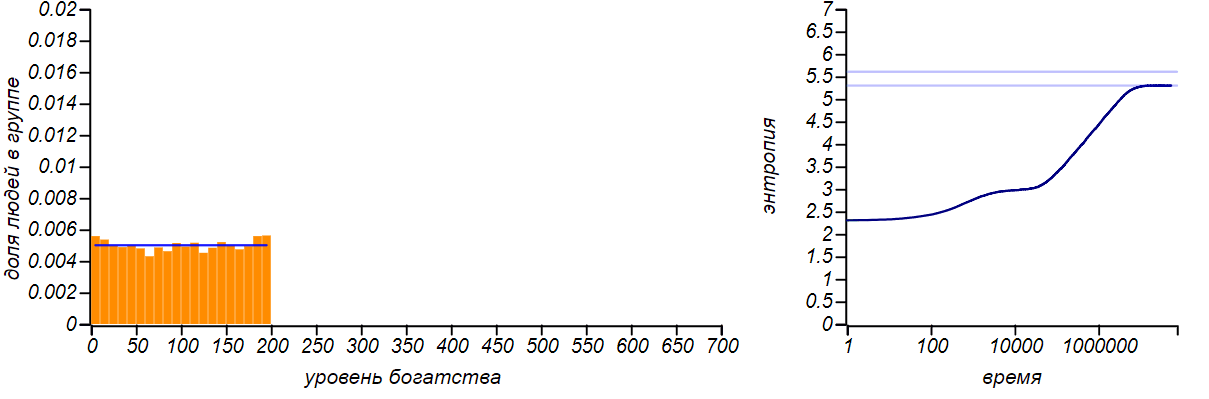
Algorithme d'échange de quantités égales avec une restriction sur le dessus: xs — n , m , xMax — .
i <- 0 n xs[i] > 0 j <- 0 n xs[j] < xMax xs[i] <- xs[i] - 1 xs[j] <- xs[j] + 1
Et que se passera-t-il si la symétrie est rompue, c'est-à-dire si nous déplaçons la bordure droite vers la droite ou la gauche?<\ br>Variantes de distributions bornées asymétriques par rapport aux distributions de Bernoulli correspondant au décalage de la valeur moyenne. Les lignes horizontales sur les graphiques d'entropie indiquent les valeurs théoriques de l'entropie des distributions de Bernoulli.La répartition des richesses a cessé d'être uniforme, prenant la forme d'une exponentielle limitée. Avec le déplacement de la frontière droite vers la gauche, l'équilibre des joueurs riches est devenu plus que pauvre. Si nous «dégrossissons» l'histogramme avec seulement deux colonnes à gauche, nous obtenons la distribution de Bernoulli montrant la probabilité qu'il soit conditionnellement «pauvre» ou «riche». Lorsque les valeurs d'une variable aléatoire sont limitées à seulement deux valeurs, la distribution de Bernoulli est le seul choix; elle délivre bien sûr un maximum d'entropie. Mais attention au fait que l'entropie de nos distributions de modèles tend précisément aux valeurs prédites par la distribution de Bernoulli. Les coefficients de Gini pour ces deux cas sont égaux0.43 et
0.2 , respectivement.L'entropie mystérieuse et puissante est, bien sûr, cool et, peut-être, même convaincante. Mais pourquoi, avec un échange symétrique, les pauvres deviennent-ils plus riches que les riches? Pourquoi le mode de distribution d'équilibre est-il égal à zéro? Il est nécessaire, comme disent les physiciens, de comprendre la cinétique du processus, c'est-à-dire le destin des particules individuelles. Nous ne nous sommes pas trompés en supposant que le modèle de marche aléatoire décrit un changement dans l'état d'un soumissionnaire individuel: il est également susceptible de prendre des mesures à la fois vers le haut et vers le bas. Et pour la marche aléatoire, une célèbre loi de la méchanceté est remplie: la malédiction du joueur. Permettez-moi de vous rappeler qu'elle consiste dans le fait qu'avec une observation suffisamment longue, une particule errante au hasard sera nécessairement en tout endroit indiqué à l'avance.De plus, la distance à laquelle la particule s'éloigne de tout point de départ est proportionnelle à la racine carrée du nombre de pas. Tout cela conduit au fait que si une particule commence son chemin près de zéro, alors elle l'atteindra très probablement, et puisque zéro dans notre problème est une frontière impénétrable, elle sera obligée de recommencer son chemin encore et encore près du point zéro, expérimentant la malédiction notoire. À mesure que la particule s'éloigne de zéro, la probabilité d'y retourner diminue et les riches deviennent plus susceptibles de sauver leur condition. Mais alors, qu'est-ce qui empêche la particule de s'éloigner arbitrairement loin, et à un joueur particulier de devenir arbitrairement riche? En fait, rien que la finitude de l'argent dans le système - la distribution exponentielle est différente de zéro sur tout l'axe positif.Mais pour atteindre une richesse incroyable selon les règles de notre jeu, il est nécessaire que tous les joueurs choisissent au hasard le même joueur encore et encore. Et pour la première fois, la probabilité d'un tel choix est(1/n)n−1- un milliardième pour un groupe de dix personnes, et c'est par hasard de le répéter plusieurs fois, c'est complètement incroyable. Le choix de la personne à qui donner de l'argent dans notre modèle incombe à tout le monde, ce qui signifie qu'il deviendra non seulement riche mais aussi pauvre. Il y a de la justice dans ce monde! Bien que triomphant pas pour longtemps, si vous n'êtes pas riche.L'économie doit être économique
Tant que notre modèle d'échange ne prend pas en compte la prospérité des acteurs, il reste irréaliste. En fait, les riches dépensent plus et les pauvres dépensent moins, d'ailleurs, les gens raisonnables essaient de maintenir une partie de leur fortune. Comme prochaine complication du modèle, exigons que les joueurs donnent une certaine part connue lors de l'échangeαson état. Un nouveau paramètre et une nouvelle restriction sont introduits dans le système, par conséquent, l'état d'équilibre peut s'écarter de celui exponentiel. En utilisant des fractions du niveau de bien-être, nous passons à des caractéristiques multiplicatives, telles que, par exemple, le retour sur investissement, le retour sur investissement, etc. Tous les manuels d'économie indiquent que si vous voulez calculer le retour sur investissement moyen, par exemple, sur plusieurs années, vous devez calculer la moyenne géométrique des rendements de chaque année. Dans notre cas, la moyenne géométrique est déterminée de manière unique, mais non triviale, par la valeurα .
Ainsi, en ajoutant un nouveau paramètre, nous fixons la distribution géométrique moyenne du revenu des joueurs, ou le rendement moyen du modèle de marché. Par conséquent, nous pouvons nous attendre à ce que la distribution d'équilibre de la richesse soit bien décrite par la distribution gamma. On peut en être convaincu, après avoir réalisé une modélisation par simulation.Si les coûts de l'échange sont proportionnels à l'abondance, la distribution d'équilibre tend vers une distribution gamma caractéristique en forme de cloche asymétrique. Dans ce modèle α=1/3 . Le rendement de change moyen était 75% .Algorithme d'échange proportionnel: xs — n , m , alpha — , .
i <- 0 n xs[i] > 0 dx <- floor(xs[i]*alpha) xs[i] <- xs[i] - dx j <- 0 n xs[j] <- xs[j] + dx
La diminution de la part des pauvres est due au fait qu'ils dépensent en moyenne moins que ce qu'ils reçoivent des riches, car tous deux échangent des parts de leur capital. Mais cet ascenseur social ne fonctionne que lorsqueα<1/2 .
Si vous dépensez plus de la moitié de ce que vous avez, la probabilité d'être parmi les pauvres devient très tangible. Pour différentes valeursα Vous pouvez obtenir une distribution de formulaires très différente avec un large éventail d'injustices:Différentes options pour des distributions d'équilibre à des coûts proportionnels à la richesse. Les graphiques sont marqués de valeurs α , et sur le graphique de droite entre parenthèses sont également les valeurs de l'index de Gini.Solution exacte, , . , , , , , , . , , , .
-
Gamma(k,θ) — , ,
k=1 . , . , — . —
, - , , -. ,
X∼Gamma(k1,θ),Y∼Gamma(k2,θ)⟹X+Y∼Gamma(k1+k2,θ)
, :
X∼Gamma(k,θ)⟹aX∼Gamma(k,aθ).
m α :
Gamma(1α−1,1m(1α−1)) .
On peut voir que plus une partie des acteurs du capital est obligée de dépenser (par exemple, pour les besoins quotidiens ou la nourriture), plus la proportion de pauvres augmente et moins la société devient équitable. Curieux qu'avecα=1/2la distribution d'équilibre devient exponentielle, comme dans le modèle à échange égal. La distribution exponentielle est un cas particulier de la distribution gamma, donc cette transformation, en soi, n'est pas surprenante. Mais il y a une subtilité curieuse: l'entropie de ce cas particulier est plus que l'entropie des distributions avec d'autres valeursα .
Voyez comment l'entropie change à mesure que la situation évolue α=0.75 :
Dans le processus de transition vers l'équilibre, le système «saute» l'état avec une entropie maximale.Dans un premier temps, la valeur de l'entropie augmente de façon monotone, puis, sans atteindre un maximum théorique correspondant à la distribution exponentielle, elle s'arrête et commence à diminuer. Y a-t-il une contradiction avec la définition d'un état d'équilibre comme un état avec un maximum d'entropie? Il n'y a pas de contradiction, puisque l'état d'équilibre doit être stationnaire, c'est-à-dire qu'il ne crée pas de flux d'énergie dirigés et est stable, ou, en parlant le langage de la théorie des systèmes dynamiques, attirant un système à lui-même. Et de tout équilibre stationnaire sera l'état d'entropie maximale. Et dans notre casα=0.75, la distribution exponentielle correspond à un état instationnaire.Des chercheurs de l'Université de Boston Ispolatov et Krapivsky ont compliqué le modèle d'échange proportionnel de telle manière que l'échange prend en compte non seulement le bien-être des dépenses, mais aussi les recettes. Un millionnaire achète rarement quelque chose à un marchand de légumes, et un marchand de légumes a rarement beaucoup de revenus, d'autre part, un constructeur automobile extra-classe n'interagira qu'avec des clients riches, mais lui-même ne sera pas non rentable. Et donc, dans les modèles dans lesquels les riches commencent à payer principalement aux riches et aux pauvres - aux pauvres, la société s'effondre complètement.Si les flux de trésorerie deviennent dépendants du capital, le système perd sa stabilité et conduit à un appauvrissement constant du groupe et à une augmentation des inégalités de classe. Dans cet exemple α=0.3,β=0.1 (. ).-: xs — n , m , alpha — , , beta — , .
i <- 0 n xs[i] > 0 dx <- floor(xs[i]*alpha) xs[i] <- xs[i] - dx dx > 0 j <- 0 n d = min(dx, floor(xs[j]*beta)) xs[j] <- xs[j] + d dx <- dx - d
Dans ce système, il n'y a qu'un seul état stationnaire: lorsque tous les joueurs n'ont (et donc ne reçoivent pas) absolument rien, et que toute la richesse va à quelqu'un seul. Le coefficient de Gini dans cet état est presque égal à l'unité, et il est très loin de l'équilibre normal - son entropie est presque nulle. La situation peut être sauvée par une restriction d'en bas, qui interdit aux joueurs de perdre absolument toutes leurs économies, auquel cas la distribution d'équilibre redevient exponentielle ou en forme de gamma. Nous pouvons également introduire une restriction par le haut - nous obtenons alors une certaine distribution asymétrique correspondant à la distribution de Bernoulli. Le modèle d'un tel marché sauvage est tout à fait applicable au marché des valeurs mobilières sans aucune restriction, mais ils ont du mal avec cela sur les échanges réels, introduisant des restrictions sur le volume des transactions,engagés par jour et à des niveaux de croissance maximum ou de baisse du prix d'un actif.Toutes ces conclusions sont tristes, ne parlant pas en faveur du marché libre, ou est-ce le cas, le modèle proposé par Sharikov! Mais qu'est-ce que l'entropie d'une distribution dégénérée? Selon la formule standard, c'est exactement zéro. Il s'agit de la répartition la plus déséquilibrée et la plus improbable, et dans tout modèle d'échange, elle est instable, de sorte qu'une telle société ne peut être obtenue que artificiellement. Le marché sauvage, bien sûr, n'est pas un cadeau - il est instable et tend à accentuer les inégalités. Il faut beaucoup de restrictions mutuellement convenues et des relations finement ajustées pour construire un marché durable et une société plus ou moins juste. L'humanité explore cette question depuis très peu de temps et, fondamentalement, au toucher, par essais et erreurs, mais une chose est claire: l'injustice dans l'espace économique n'est pas une conséquence de la nature humaine sale, mais une propriété objective du système.dont nous faisons tous partie. De plus, les tentatives de créer une justice absolue dans un style sharikov allaient toujours de pair avec la bataille et le sang, et les résultats, en raison de son déséquilibre, n'existaient pas longtemps.Il est peu probable que les molécules et les atomes parlent de l'injustice de leur monde, et les physiciens et les ingénieurs ont accepté pendant deux cents ans que, quel que soit le moteur thermique idéal qu'ils ont construit, le chaos ne permettra pas à la chaleur d'être convertie de fonctionner plus que la part requise. Quand c'est clair, ce n'est pas si offensant. J'espère que ce chapitre aide un lecteur curieux à comprendre et à accepter notre monde complexe et injuste.