Quand mon premier fils n'avait que deux ans, il aimait déjà les voitures, connaissait toutes les marques et modèles (encore plus que moi, grâce à mes amis), pouvait les reconnaître par une petite partie de l'image. Tout le monde a dit: génie. Bien qu'ils aient noté la futilité totale de cette connaissance. Et le fils, pendant ce temps, dormait avec eux, les roulait, les disposait exactement dans une rangée ou un carré.

Quand il avait 4 ans, il a appris à compter, et à 5 ans, il pouvait déjà se multiplier et ajouter jusqu'à 1000. Nous avons même joué à Math Workout (le jeu est comme ça sur Android - j'aimais calculer dans le métro après le travail), et à un moment donné, il a commencé à me faites juste ça. Et pendant son temps libre, il a compté jusqu'à un million, qui s'est figé. Un génie! Ils ont dit, mais nous pensions que ce n'était pas du tout.
Soit dit en passant, sur le marché, il a bien aidé sa mère - il a calculé le montant total plus rapidement que les vendeurs sur la calculatrice.
De plus, il n'a jamais joué sur le terrain, ne communiquait pas avec ses pairs, ne s'entendait pas très bien avec les enfants et les enseignants du jardin. En général, j'étais un petit enfant réservé.
L'étape suivante était la géographie - nous avons essayé de canaliser l'amour des nombres quelque part et avons remis à notre fils un vieil atlas soviétique. Il s'y est plongé pendant un mois, puis a commencé à nous poser des questions délicates dans le style de:
- Papa, selon toi, quel pays a une grande superficie: le Pakistan ou le Mozambique?
«Probablement le Mozambique», ai-je répondu.
- Ça y est! La superficie du Pakistan est de 2 350 km2 », a répondu le fils avec joie.

En même temps, il ne s'intéressait absolument pas aux peuples vivant dans ces pays, ni à leurs langues, ni à leurs vêtements, ni à la musique folklorique. Seuls les chiffres nus: superficie, population, volume des réserves minérales, etc.
Tout le monde a de nouveau admiré. "Je suis intelligent au-delà de mes années", ont-ils dit autour, mais encore une fois, j'étais inquiet, car J'ai compris qu'il s'agissait de connaissances totalement inutiles, non liées à l'expérience de vie, et qu'il était difficile de continuer à développer. La meilleure application de tout ce que j'ai trouvé était une proposition pour calculer le nombre de voitures dans le parking, si un pays particulier était roulé avec de l'asphalte (sans tenir compte du terrain montagneux), mais rapidement arrêté, car ça sent le génocide.
Fait intéressant, le sujet des voitures à ce moment-là a complètement disparu, le fils ne se souvenait même pas du nom de ses voitures préférées de son énorme collection, que nous avons commencé à distribuer avec perte d'intérêt. Et puis il a commencé à compter lentement dans son esprit et a vite oublié la région des pays. En même temps, il a commencé à communiquer davantage avec ses pairs, est devenu plus de contact. Le génie passa, les amis cessèrent d'admirer, le fils devint juste un bon élève avec un penchant pour les mathématiques et les sciences exactes.
Répétition - la mère de l'apprentissage
Il semblerait, pourquoi tout cela. Cela est observé chez de nombreux enfants. Leurs parents déclarent à tout le monde que leurs enfants sont géniaux, les grands-mères sont enthousiastes et félicitent les enfants pour leur «savoir». Et puis de simples enfants intelligents ordinaires sortent d'eux, pas plus brillants que l'ami du fils de la mère.
En étudiant les réseaux de neurones, je suis tombé sur un phénomène similaire, et il me semble que certaines conclusions peuvent être tirées de cette analogie. Je ne suis ni biologiste ni neuroscientifique. Plus loin - mes suppositions sans prétendre être particulièrement scientifique. Je serai heureux de commenter les professionnels.
Quand j'ai essayé de comprendre comment mon fils avait appris si rapidement à compter plus vite que moi (il a passé le niveau de Math Workout en 20,4 secondes, alors que mon record était de 21,9), j'ai réalisé qu'il ne comptait pas du tout. Il a mémorisé que lorsque 55 + 17 apparaît, vous devez appuyer sur 72. À 45 + 38, vous devez cliquer sur 83, et ainsi de suite. Au début, il comptait certainement, mais la poussée de vitesse s'est produite au moment où il a pu se souvenir de toutes les combinaisons. Et assez rapidement, il a commencé à se souvenir non pas d'inscriptions concrètes, mais de combinaisons de symboles. C'est exactement ce qui est enseigné à l'école, en étudiant la table de multiplication - rappelez-vous la table de correspondance MxN -> P.
Il s'est avéré qu'il percevait la plupart des informations précisément comme une relation entre l'entrée et la sortie, et que l'algorithme très général que nous avons utilisé pour faire défiler pour obtenir une réponse ne se limitait pas à un algorithme hautement spécialisé très bien affiné pour calculer des nombres à deux chiffres. Il a fait un peu d'excellentes tâches, mais beaucoup plus lentement. C'est-à-dire ce qui semblait super cool pour tout le monde était en fait juste simulé par un réseau neuronal bien formé pour une tâche spécifique.
Connaissances supplémentaires
Pourquoi certains enfants ont-ils la capacité de s'en souvenir, alors que d'autres ne le font pas?
Imaginez le champ d'intérêt de l'enfant (ici nous abordons la question qualitativement, sans aucune mesure). A gauche se trouve le champ des intérêts d'un enfant ordinaire, et à droite se trouve le champ des intérêts d'un enfant «doué». Comme prévu, le principal intérêt se concentre dans les domaines où les inclinations spéciales. Mais sur les choses de tous les jours et la communication avec les pairs, l'attention ne suffit plus. Il considère cette connaissance superflue.
 |  |
| Intérêts d'un enfant ordinaire de 5 ans | L'intérêt de l'enfant "brillant" de 5 ans |
Chez de tels enfants, le cerveau analyse et conduit la formation uniquement sur des sujets sélectionnés. Grâce à la formation, un réseau neuronal dans le cerveau doit apprendre à classer avec succès les données entrantes. Mais le cerveau possède de très nombreux neurones. Vraiment plus que nécessaire pour un travail normal avec des tâches aussi simples. Habituellement, dans la vie, les enfants résolvent de nombreux problèmes différents, mais ici, les mêmes ressources sont affectées à un éventail de tâches plus restreint. Et la formation dans ce mode conduit facilement à ce que les professionnels du ML appellent le sur-ajustement. Le réseau, en utilisant une abondance de coefficients (neurones), a été formé de telle manière qu'il donne toujours exactement les bonnes réponses (mais il peut donner un non-sens complet sur les données d'entrée intermédiaires, mais personne ne le voit). Ainsi, la formation n'a pas conduit au fait que le cerveau a distingué les principales caractéristiques et les a mémorisées, mais au fait qu'il a ajusté beaucoup de coefficients afin de produire un résultat exact sur des données déjà connues (comme dans l'image de droite). De plus, sur d'autres sujets, le cerveau a appris ainsi, mal formé (comme dans l'image de gauche).
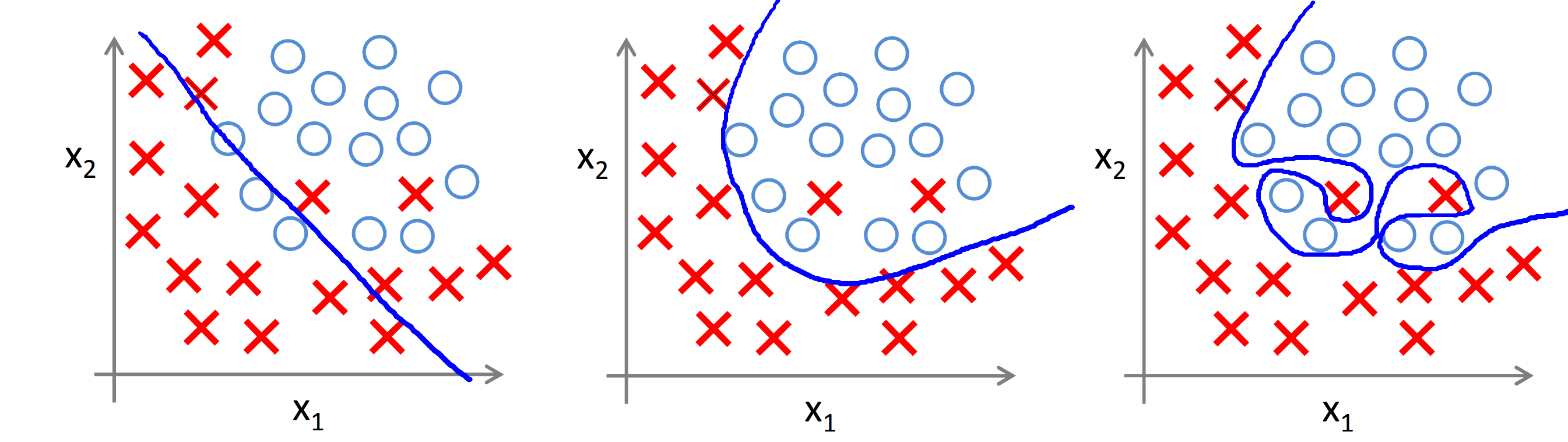
Qu'est-ce que le sous-ajustement et le sur-ajustement?Pour ceux qui ne sont pas dans le sujet, je vous le dirai très brièvement. Lors de la formation d'un réseau de neurones, la tâche consiste à sélectionner un certain nombre de paramètres (poids de communication entre les neurones) afin que le réseau, répondant aux données de formation (échantillon de formation), réponde le plus précisément et le plus précisément possible.
S'il y a trop peu de tels paramètres, le réseau ne pourra pas prendre en compte les détails de l'échantillon, ce qui conduira à une réponse très approximative et moyenne qui ne fonctionne pas bien même dans l'échantillon d'apprentissage. Comme dans l'image de gauche ci-dessus. C'est insuffisant.
Avec un nombre adéquat de paramètres, le réseau donnera un bon résultat, «avalant» de fortes déviations dans les données d'entraînement. Un tel réseau répondra bien non seulement à l'ensemble de formation, mais aussi à d'autres valeurs intermédiaires. Comme dans l'image du milieu ci-dessus.
Mais si le réseau reçoit trop de paramètres configurables, il est alors formé pour reproduire même les écarts et fluctuations importants (y compris ceux causés par des erreurs), ce qui peut conduire à des détritus complets lorsque vous essayez d'obtenir une réponse aux données d'entrée ne provenant pas de l'ensemble de formation. Comme dans l'image ci-dessus. C'est exagéré.
Un exemple illustratif simple.

Imaginez que vous avez plusieurs points (cercles bleus). Vous devez dessiner une courbe lisse qui vous permet de prédire la position des autres points. Si nous prenons, par exemple, un polynôme, puis pour les petits degrés (jusqu'à 3 ou 4), notre courbe lisse sera assez précise (courbe bleue). Dans ce cas, la courbe bleue peut ne pas passer par les points de départ (point bleu).
Cependant, si le nombre de coefficients (et donc le degré du polynôme) augmente, la précision du passage des points bleus augmentera (ou il y aura même un hit à 100%), mais le comportement entre ces points deviendra imprévisible (voir comment la courbe rouge fluctue).
Il me semble que c’est l’inclinaison de l’enfant à un sujet spécifique (la fixation) et le mépris total des autres sujets qui conduisent au fait qu’au cours de la formation, trop de «facteurs» sont accordés à ces mêmes sujets.
Étant donné que le réseau est configuré pour des données d'entrée spécifiques et n'a pas alloué de «fonctionnalités», mais qu'il a «bêtement» mémorisé les données d'entrée, il ne peut pas être utilisé avec des données d'entrée légèrement différentes. L'applicabilité d'un tel réseau est très étroite. Avec l'âge, l'horizon s'élargit, le foyer s'érode et il n'y a plus de possibilité d'affecter autant de neurones à la même tâche - ils commencent à être utilisés dans de nouvelles tâches plus nécessaires à l'enfant. Les «paramètres» de ce réseau surchargé s'effondrent, l'enfant devient «normal», le génie disparaît.
Bien sûr, si un enfant a une compétence qui est utile en soi et peut être développée (par exemple, la musique ou le sport), alors son «génie» peut être maintenu pendant longtemps, et même amener ces compétences à un niveau professionnel. Mais dans la plupart des cas, cela ne fonctionne pas, et à partir des compétences passées et une trace ne restera pas à l'âge de 8 à 10 ans.
Conclusions
- avez-vous un enfant brillant? ça va passer;)
- les horizons et le «génie» sont des choses liées, et ils sont connectés précisément par le mécanisme d'apprentissage
- ce "génie" visible - probablement pas du tout génial, mais l'effet de trop d'entraînement cérébral sur une tâche particulière sans le comprendre - c'est juste que toutes les ressources ont été consacrées à cette tâche
- en corrigeant les intérêts étroits de l'enfant, son génie disparaît
- si votre enfant est «ingénieux» et un peu plus réservé que ses pairs, alors vous devez développer ces mêmes compétences avec soin, développer activement vos horizons en même temps, et ne pas vous concentrer sur ces compétences «cool» mais généralement inutiles