Répartissez uniformément les points à travers la sphère en pytorch et tensorflow

Ce texte est écrit pour ceux qui s'intéressent à l'apprentissage en profondeur, qui souhaitent utiliser différentes méthodes des bibliothèques pytorch et tensorflow pour minimiser la fonction de nombreuses variables, qui souhaitent apprendre à transformer un programme exécuté séquentiellement en calculs matriciels vectorisés effectués à l'aide de numpy. Vous pouvez également apprendre à créer un dessin animé à partir de données visualisées à l'aide de PovRay et de vapory.

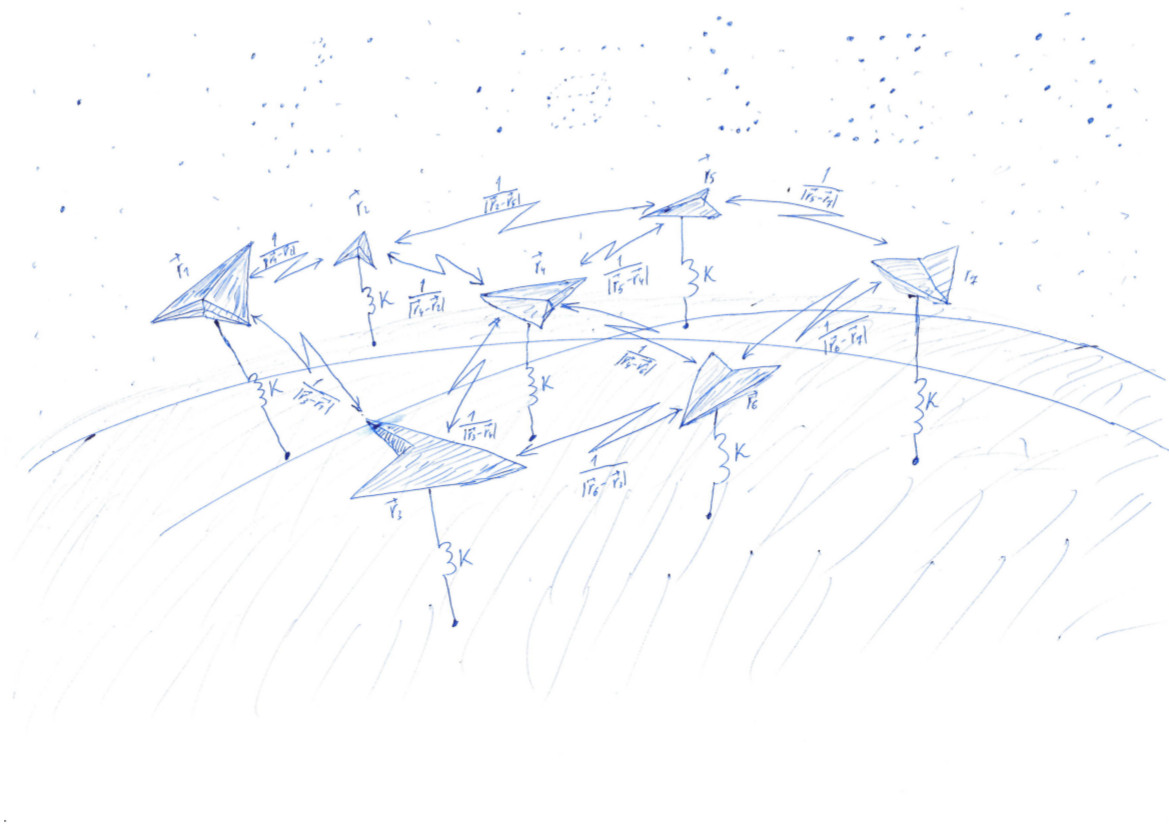
D'où vient la tâche

Chacun minimise ses fonctionnalités (c) Data Scientist anonyme

Dans l' une des publications précédentes de notre blog , à savoir dans le paragraphe "Rake No. 6", nous avons parlé de la technologie DSSM, qui vous permet de convertir du texte en vecteurs. Pour trouver une telle cartographie, il faut trouver les coefficients de transformations linéaires qui minimisent la fonction de perte plutôt complexe. Il est difficile de comprendre ce qui se passe lors de l'apprentissage d'un tel modèle en raison de la grande dimensionnalité des vecteurs. Pour développer une intuition qui vous permet de choisir la méthode d'optimisation et de définir les paramètres de cette méthode, vous pouvez envisager une version simplifiée de cette tâche. Maintenant, laissez les vecteurs dans notre espace tridimensionnel habituel, alors ils sont faciles à dessiner. Et la fonction de perte sera le potentiel d'écarter les points et d'attirer la sphère unitaire. Dans ce cas, la solution au problème sera une distribution uniforme des points sur la sphère. La qualité de la solution actuelle est facile à évaluer à l'œil nu.

Nous chercherons donc une distribution uniforme sur la sphère d'une quantité donnée $$$n$des points. Une telle distribution est parfois nécessaire à l'acoustique pour comprendre dans quelle direction lancer une onde dans un cristal. Signalman - pour savoir comment mettre des satellites en orbite pour obtenir des communications de la meilleure qualité. Météorologue - pour le placement de stations de surveillance météorologique.

Pour certains $$$n$la tâche est résolue facilement . Par exemple, si $$$n = 8$, nous pouvons prendre le cube et ses sommets seront la réponse au problème. Nous avons aussi de la chance si $$$n$sera égal au nombre de sommets de l'icosaèdre, du dodécaèdre ou d'un autre solide platonicien. Sinon, la tâche n'est pas si simple.

Pour un nombre de points suffisamment important, il existe une formule avec des coefficients sélectionnés empiriquement , plusieurs autres options sont ici , ici , ici et ici . Mais il existe une solution plus universelle, quoique plus complexe, à laquelle cet article est consacré.

Nous résolvons un problème très similaire au problème de Thomson ( wiki ). Scatter $$$n$les points au hasard, puis les faire attirer vers une surface, telle qu'une sphère, et se repousser les uns des autres. L'attraction et la répulsion sont déterminées par la fonction - potentiel. À la valeur minimale de la fonction potentielle, les points se trouveront sur la sphère le plus uniformément.

Cette tâche est très similaire au processus d'apprentissage des modèles d'apprentissage automatique (ML), au cours duquel la fonction de perte est minimisée. Mais un data scientist observe généralement comment un nombre unique diminue, et nous pouvons regarder l'image changer. Si nous réussissons, nous verrons comment les points placés aléatoirement à l'intérieur du cube avec le côté 1 divergent le long de la surface de la sphère:

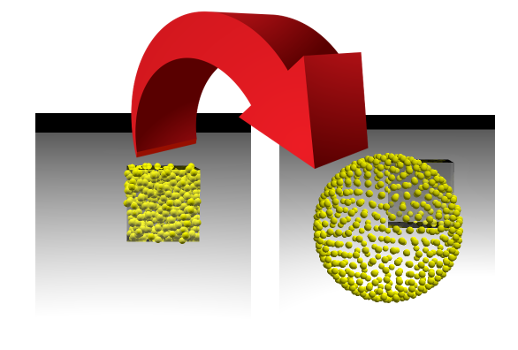
Schématiquement, l'algorithme de résolution du problème peut être représenté comme suit. Chaque point situé dans l'espace tridimensionnel correspond à une ligne de la matrice $$$X$. La fonction de perte est calculée à partir de cette matrice. $$$L$, dont la valeur minimale correspond à une répartition uniforme des points sur la sphère. La valeur minimale est trouvée en utilisant les tensorflow pytorch et tensorflow , qui permettent de calculer le gradient de la fonction de perte par la matrice $$$X$et descendre au minimum en utilisant l'une des méthodes implémentées dans la bibliothèque: SGD, ADAM, ADAGRAD, etc.

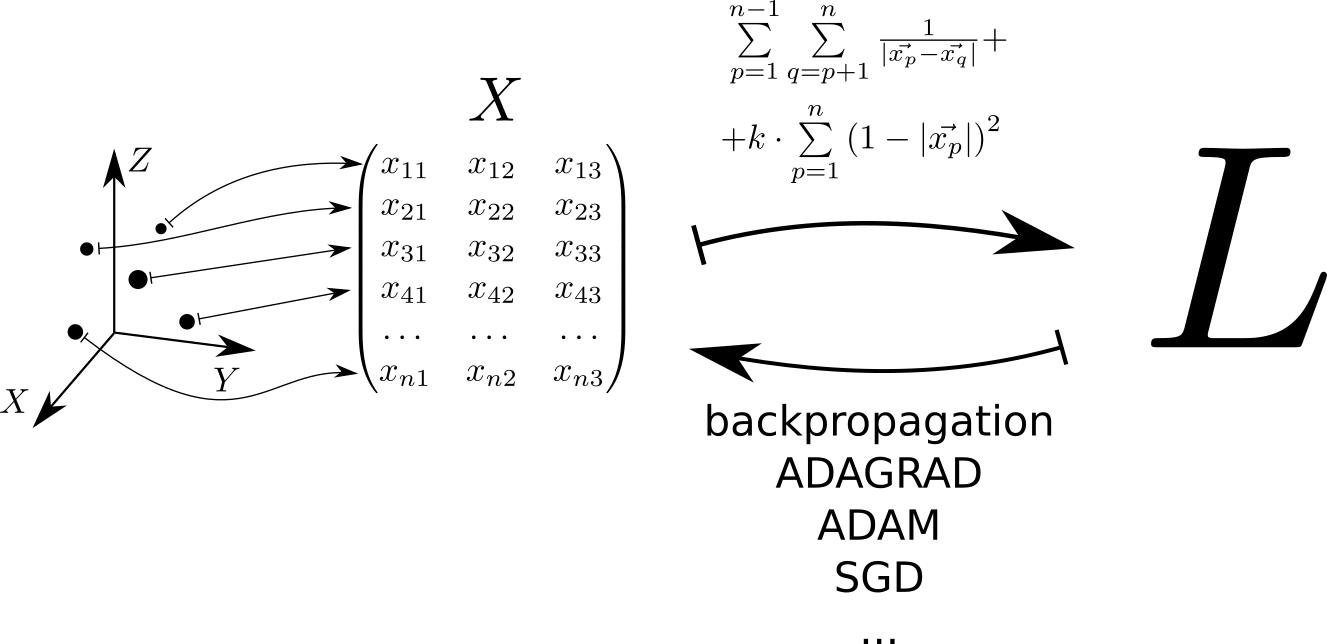
Nous considérons le potentiel

En raison de sa simplicité, de son expressivité et de sa capacité à servir d'interface avec des bibliothèques écrites dans d'autres langages, Python est largement utilisé pour résoudre les problèmes d'apprentissage automatique. Par conséquent, les exemples de code de cet article sont écrits en Python. Pour les calculs matriciels rapides, nous utiliserons la bibliothèque numpy. Pour minimiser la fonction de nombreuses variables - pytorch et tensorflow.

Nous diffusons au hasard des points dans le cube de côté 1. Soit 500 points, et l'interaction élastique est 1000 fois plus importante que l'électrostatique:

 import numpy as np n = 500 k = 1000 X = np.random.rand(n, 3) 

Ce code a généré une matrice $$$X$la taille $$$3 \ fois n$rempli de nombres aléatoires de 0 à 1:

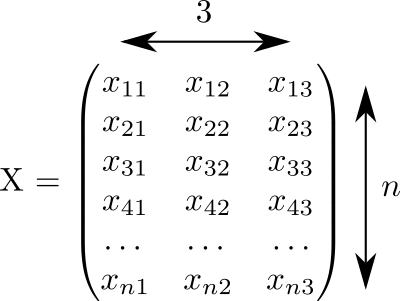
Nous supposons que chaque ligne de cette matrice correspond à un point. Et dans trois colonnes les coordonnées sont enregistrées $$$x, y, z$tous nos points.

Le potentiel d'interaction élastique d'un point avec la surface d'une sphère unitaire $$$u_1 = k \ cdot (1 - r) ^ 2/2$. Potentiel d'interaction électrostatique des points $$$p$et $$$q$- $$$u_2 = 1 / | r_p - r_q |$. Le plein potentiel consiste en l'interaction électrostatique de toutes les paires de points et l'interaction élastique de chaque point avec la surface de la sphère:

$$

$$U (x_1, ..., x_n) = \ sum \ limits _ {p = 1} ^ {n - 1} \ sum \ limits _ {q = p + 1} ^ {n} \ frac 1 {\ left | \ vec {x_p} - \ vec {x_q} \ right | } + k \ cdot \ sum \ limits _ {p = 1} ^ n \ left (1 - | \ vec {x_p} | \ right) ^ 2 \ rightarrow \ min$$

En principe, la valeur potentielle peut être calculée à l'aide de cette formule:

 L_for = 0 L_for_inv = 0 L_for_sq = 0 for p in range(n): p_distance = 0 for i in range(3): p_distance += x[p, i]**2 p_distance = math.sqrt(p_distance) L_for_sq += k * (1 - p_distance)**2 #     ,     for q in range(p + 1, n): if q != p: pq_distance = 0 for i in range(3): pq_distance += (x[p, i] - x[q, i]) ** 2 pq_distance = math.sqrt(pq_distance) L_for_inv += 1 / pq_distance #      L_for = (L_for_inv + L_for_sq) / n print('loss =', L_for) 

Mais il y a un petit problème. Pour 2000 points pathétiques, ce programme fonctionnera pendant 2 secondes. Ce sera beaucoup plus rapide si nous calculons cette valeur à l'aide de calculs matriciels vectorisés. L'accélération est obtenue à la fois par la mise en œuvre d'opérations matricielles utilisant les langages «rapides» fortran et C, et par l'utilisation d'opérations de processeur vectorisées qui permettent d'effectuer une action sur une grande quantité de données d'entrée en un cycle d'horloge.

Regardons la matrice $$$S = X \ cdot X ^ T$. Il possède de nombreuses propriétés intéressantes et se retrouve souvent dans les calculs liés à la théorie des classificateurs linéaires en ML. Donc, si nous supposons que dans la ligne de la matrice $$$X$avec indices $$$p$et $$$q$les vecteurs spatiaux tridimensionnels sont écrits $$$\ vec {r _ p}, \ vec {r_q}$puis la matrice $$$S$consistera en produits scalaires de ces vecteurs. Ces vecteurs $$$n$pièces, puis la dimension de la matrice $$$S$est égal à $$$n \ fois n$.

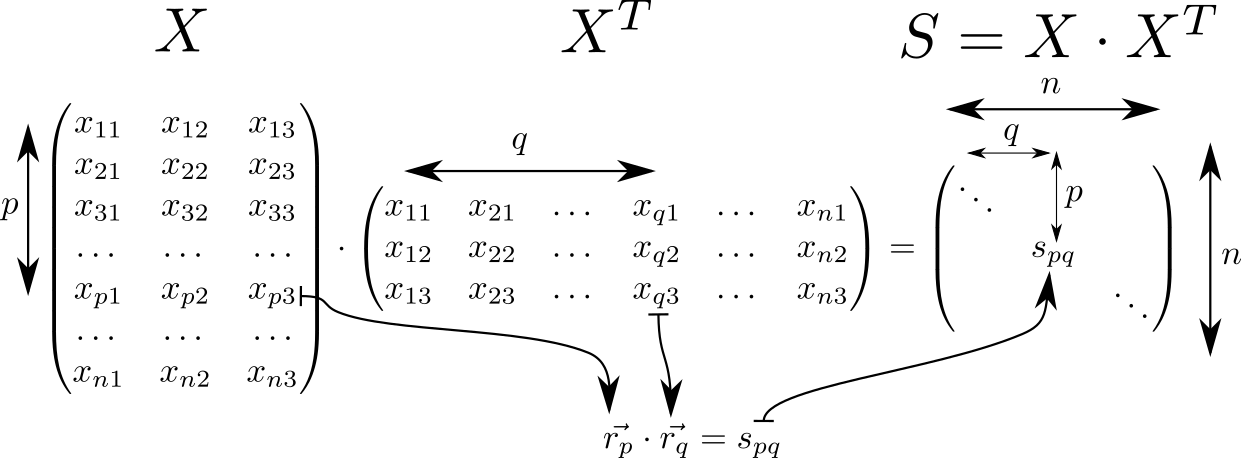
Sur la diagonale de la matrice $$$S$tenir des carrés de longueurs de vecteurs $$$\ vec {r_p}: s_ {p p} = r_p ^ 2$. Sachant cela, considérons le plein potentiel de l'interaction. Nous commençons par calculer deux matrices auxiliaires. Dans une matrice diagonale $$$S$sera répété en lignes, dans un autre - en colonnes.

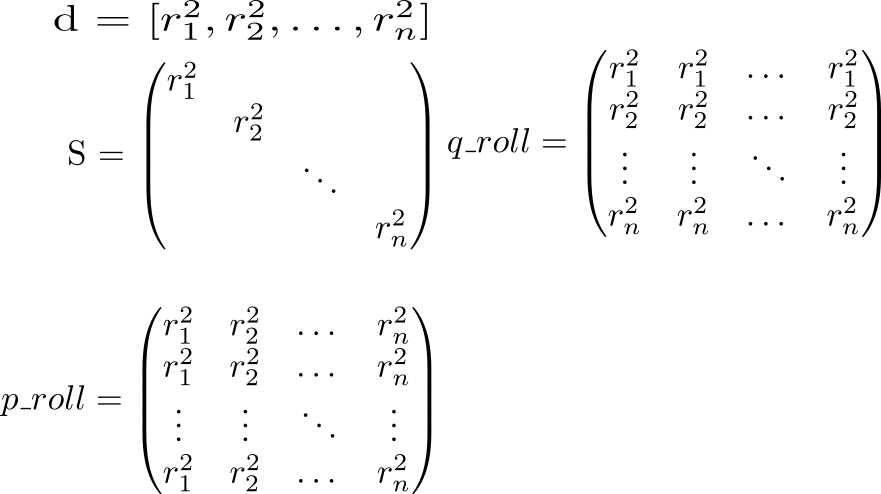
Regardons maintenant la valeur de l'expression p_roll + q_roll - 2 * S

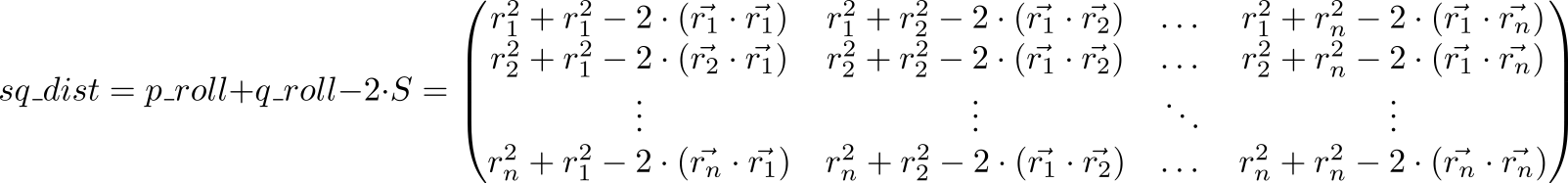
Élément indexé $$$(p, q)$matrice sq_dist est égale $$$r_p ^ 2 + r_q ^ 2 - 2 \ cdot (\ vec {r_p}, \ vec {r_q}) = (\ vec {r_p} - \ vec {r_q}) ^ 2$. Autrement dit, nous avons une matrice de carrés de distances entre les points.

Répulsion électrostatique sur une sphère

dist = np.sqrt(sq_dist) - matrice des distances entre les points. Nous devons calculer le potentiel, en tenant compte de la répulsion des points entre eux et de l'attraction vers la sphère. Mettez les unités sur la diagonale et remplacez chaque élément par son inverse (ne pensez pas que nous inversons la matrice!): rec_dist_one = 1 / (dist + np.eye(n)) . Le résultat est une matrice sur la diagonale dont il y a des unités, les autres éléments sont les potentiels de l'interaction électrostatique entre les points.

Maintenant, nous ajoutons le potentiel d'attraction quadratique à la surface de la sphère unitaire. La distance de la surface de la sphère $$$(1 - r)$. Carré et multipliez par $$$k$, qui définit la relation entre le rôle de la répulsion électrostatique des particules et l'attraction d'une sphère. Total k = 1000 , all_interactions = rec_dist_one - torch.eye(n) + (d.sqrt() - torch.ones(n))**2 . La fonction de perte tant attendue, que nous minimiserons: t = all_interactions.sum()

Un programme qui calcule le potentiel à l'aide de la bibliothèque numpy:

 S = X.dot(XT) #    pp_sq_dist = np.diag(S) #  p_roll = pp_sq_dist.reshape(1, -1).repeat(n, axis=0) #     q_roll = pp_sq_dist.reshape(-1, 1).repeat(n, axis=1) #     pq_sq_dist = p_roll + q_roll - 2 * S #      pq_dist = np.sqrt(pq_sq_dist) #    pp_dist = np.sqrt(pp_sq_dist) #      surface_dist_sq = (pp_dist - np.ones(n)) ** 2 #       rec_pq_dist = 1 / (pq_dist + np.eye(n)) - np.eye(n) #      L_np_rec = rec_pq_dist.sum() / 2 #     L_np_surf = k * surface_dist_sq.sum() #       L_np = (L_np_rec + L_np_surf) / n #   ,     print('loss =', L_np) 

Ici, les choses vont un peu mieux - 200 ms à 2000 points.

Nous utilisons pytorch:

 import torch pt_x = torch.from_numpy(X) # pt_x -   tensor   pytorch pt_S = pt_x.mm(pt_x.transpose(0, 1)) # mm - matrix multiplication pt_pp_sq_dist = pt_S.diag() pt_p_roll = pt_pp_sq_dist.repeat(n, 1) pt_q_roll = pt_pp_sq_dist.reshape(-1, 1).repeat(1, n) pt_pq_sq_dist = pt_p_roll + pt_q_roll - 2 * pt_S pt_pq_dist = pt_pq_sq_dist.sqrt() pt_pp_dist = pt_pp_sq_dist.sqrt() pt_surface_dist_sq = (pt_pp_dist - torch.ones(n, dtype=torch.float64)) ** 2 pt_rec_pq_dist = 1/ (pt_pq_dist + torch.eye(n, dtype=torch.float64)) - torch.eye(n, dtype=torch.float64) L_pt = (pt_rec_pq_dist.sum() / 2 + k * pt_surface_dist_sq.sum()) / n print('loss =', float(L_pt)) 

Et enfin tensorflow:

 import tensorflow as tf tf_x = tf.placeholder(name='x', dtype=tf.float64) tf_S = tf.matmul(tf_x, tf.transpose(tf_x)) tf_pp_sq_dist = tf.diag_part(tf_S) tf_p_roll = tf.tile(tf.reshape(tf_pp_sq_dist, (1, -1)), (n, 1)) tf_q_roll = tf.tile(tf.reshape(tf_pp_sq_dist, (-1, 1)), (1, n)) tf_pq_sq_dist = tf_p_roll + tf_q_roll - 2 * tf_S tf_pq_dist = tf.sqrt(tf_pq_sq_dist) tf_pp_dist = tf.sqrt(tf_pp_sq_dist) tf_surface_dist_sq = (tf_pp_dist - tf.ones(n, dtype=tf.float64)) ** 2 tf_rec_pq_dist = 1 / (tf_pq_dist + tf.eye(n, dtype=tf.float64)) - tf.eye(n, dtype=tf.float64) L_tf = (tf.reduce_sum(tf_rec_pq_dist) / 2 + k * tf.reduce_sum(tf_surface_dist_sq)) / n glob_init = tf.local_variables_initializer() #     with tf.Session() as tf_s: #     glob_init.run() #   res, = tf_s.run([L_tf], feed_dict={tf_x: x}) #   print(res) 

Comparez les performances de ces trois approches:

N	python	engourdi	pytorch	tensorflow
2000	4,03	0,083	1.11	0,205
10 000	99	2,82	2.18	7,9

Les calculs vectorisés donnent un gain de plus d'un ordre et demi décimal par rapport au code python pur. La "plaque de chaudière" en pytorch est visible: les calculs de petits volumes prennent un temps considérable, mais ils ne changent presque pas avec l'augmentation du volume des calculs.

Visualisation

De nos jours, les données peuvent être visualisées en utilisant un grand nombre de packages, tels que Matlab, Wolfram Mathematica, Maple, Matplotlib, etc., etc. Dans ces packages, il y a beaucoup de fonctions complexes qui font des choses complexes. Malheureusement, si vous faites face à une tâche simple mais non standard, vous vous retrouvez désarmé. Ma solution préférée dans cette situation est povray. Il s'agit d'un programme très puissant qui est généralement utilisé pour créer des images photoréalistes, mais il peut être utilisé comme un «assembleur de visualisation». Habituellement, quelle que soit la difficulté de la surface que vous souhaitez afficher, demandez simplement à povray de dessiner des sphères avec des centres se trouvant sur cette surface.

À l'aide de la bibliothèque de vapeurs, vous pouvez créer une scène povray directement en python, la rendre et regarder le résultat. Maintenant, cela ressemble à ceci:

L'image est obtenue comme suit:

 import vapory from PIL import Image def create_scene(moment): angle = 2 * math.pi * moment / 360 r_camera = 7 camera = vapory.Camera('location', [r_camera * math.cos(angle), 1.5, r_camera * math.sin(angle)], 'look_at', [0, 0, 0], 'angle', 30) light1 = vapory.LightSource([2, 4, -3], 'color', [1, 1, 1]) light2 = vapory.LightSource([2, 4, 3], 'color', [1, 1, 1]) plane = vapory.Plane([0, 1, 0], -1, vapory.Pigment('color', [1, 1, 1])) box = vapory.Box([0, 0, 0], [1, 1, 1], vapory.Pigment('Col_Glass_Clear'), vapory.Finish('F_Glass9'), vapory.Interior('I_Glass1')) spheres = [vapory.Sphere( [float(r[0]), float(r[1]), float(r[2])], 0.05, vapory.Texture(vapory.Pigment('color', [1, 1, 0]))) for r in x] return vapory.Scene(camera, objects=[light1, light2, plane, box] + spheres, included=['glass.inc']) for t in range(0, 360): flnm = 'out/sphere_{:03}.png'.format(t) scene = create_scene(t) scene.render(flnm, width=800, height=600, remove_temp=False) clear_output() display(Image.open(flnm)) 

À partir d'un tas de fichiers, les gifs animés sont assemblés à l'aide d'ImageMagic:

 convert -delay 10 -loop 0 sphere_*.png sphere_all.gif 

Sur github, vous pouvez voir le code de travail, dont des fragments sont donnés ici. Dans le deuxième article, je parlerai de la façon de commencer à minimiser la fonctionnalité afin que les points sortent du cube et se répartissent uniformément à travers la sphère.