Il existe un certain nombre de tâches dans lesquelles la plage de valeurs de sortie doit être limitée, tandis que les données d'entrée ne peuvent pas le garantir. En plus des situations forcées, la limitation du signal peut être une tâche orientée vers un objectif, par exemple, lors de la compression d'un signal ou de la mise en œuvre de l'effet «overdrive».
La mise en œuvre la plus simple d'une contrainte consiste à la forcer à une certaine valeur si un certain niveau est dépassé. Par exemple, pour une sinusoïde d'amplitude croissante, elle ressemblera à ceci:

Ici, la fonction Clip agit comme un limiteur, comme un argument dont le signal d'entrée et les paramètres de restriction sont transmis, et le résultat de la fonction est le signal de sortie.
Examinons le graphique de la fonction de clip séparément:
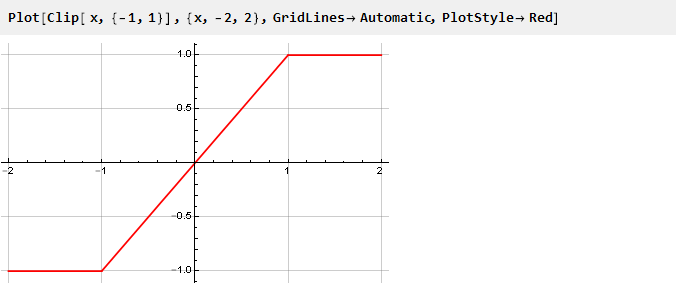
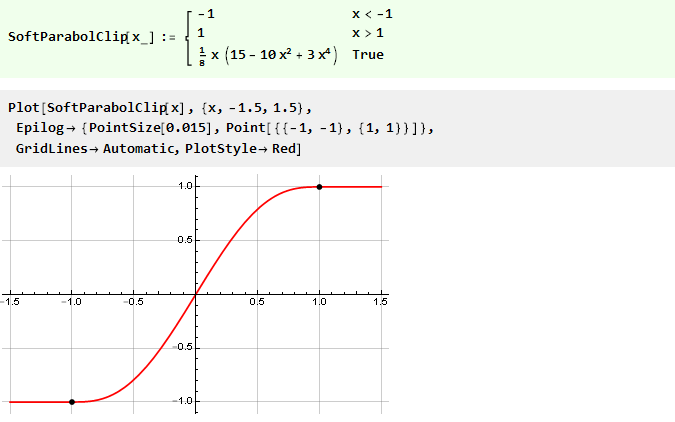
On peut en voir que si nous ne dépassons pas les limites de la limite, la valeur de sortie est égale à l'entrée et le signal ne change pas; lorsqu'elle est dépassée, la valeur de sortie ne dépend en aucune façon de l'entrée et reste au même niveau. En fait, nous avons une fonction continue par morceaux composée de trois autres: y = -1, y = x et y = 1, sélectionnées en fonction de l'argument, et équivalentes à la notation suivante:

La transition entre les fonctions se produit assez brusquement; et semble tentant de le rendre plus lisse. Mathématiquement, cette netteté est due au fait que les dérivées des fonctions aux points d'ancrage ne coïncident pas. Ceci est facile à voir en traçant la dérivée de la fonction Clip:
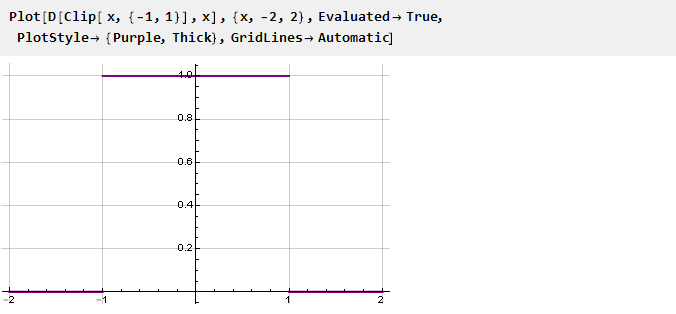
Ainsi, afin d'assurer la régularité de la fonction de contrainte, il est nécessaire d'assurer l'égalité des dérivées aux points de jonction. Et puisque les fonctions extrêmes que nous avons sont des constantes dont les dérivées sont égales à zéro, les fonctions de restriction dérivées aux points d'ancrage doivent également être égales à zéro. Ensuite, nous considérerons plusieurs de ces fonctions qui assurent un ancrage en douceur.
Sinus
Le plus simple est d'utiliser la fonction sin sur l'intervalle de -pi / 2 à pi / 2, aux frontières desquelles les valeurs de la dérivée sont égales à zéro par définition:
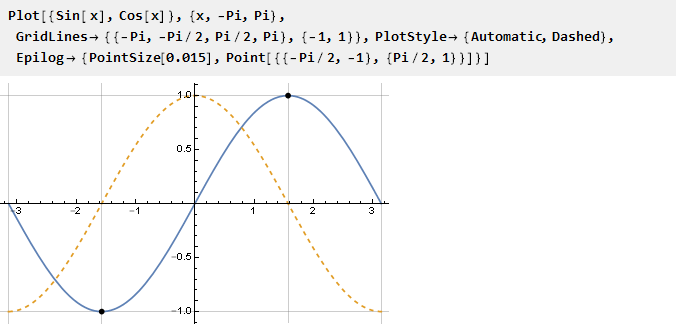
Il vous suffit de mettre à l'échelle les arguments pour que l'unité soit projetée sur le Pi / 2. Maintenant, nous pouvons définir la fonction englobante elle-même:

Et construisez son emploi du temps:
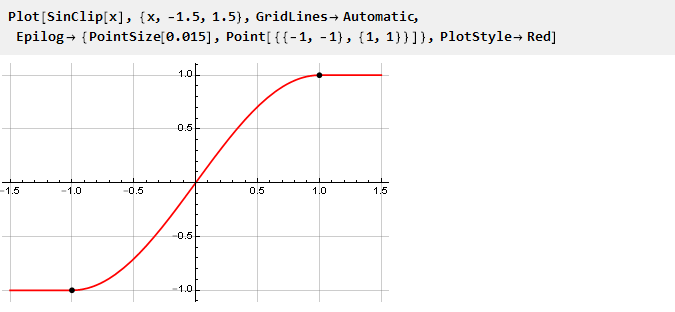
Puisque les limites de notre restriction sont strictement définies, la restriction est établie en mettant à l'échelle le signal d'entrée avec une mise à l'échelle ultérieure (si nécessaire).
Il n'y a plus non plus de situation où le signal d'entrée est transmis à la sortie sans distorsion - plus le niveau de gain est faible, plus le niveau de distorsion dû à la limitation est faible - mais le signal est de toute façon déformé.
L'effet du paramètre de gain sur la distorsion du signal peut également être vu dans la dynamique:

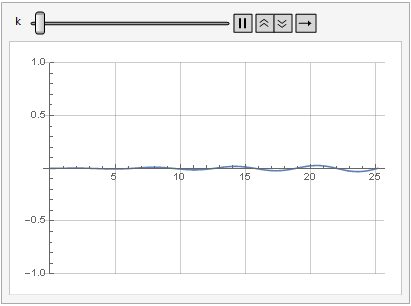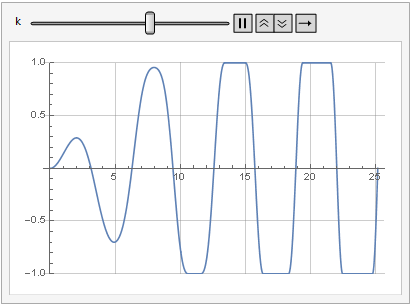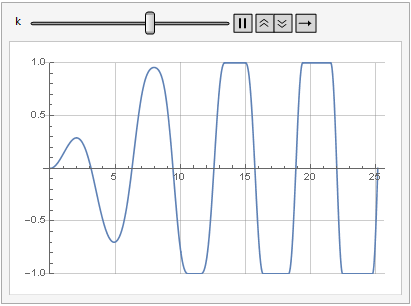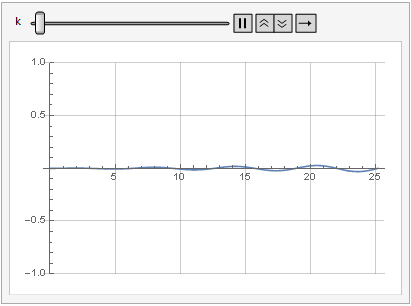
Plus de douceur
Regardons la dérivée de notre fonction:
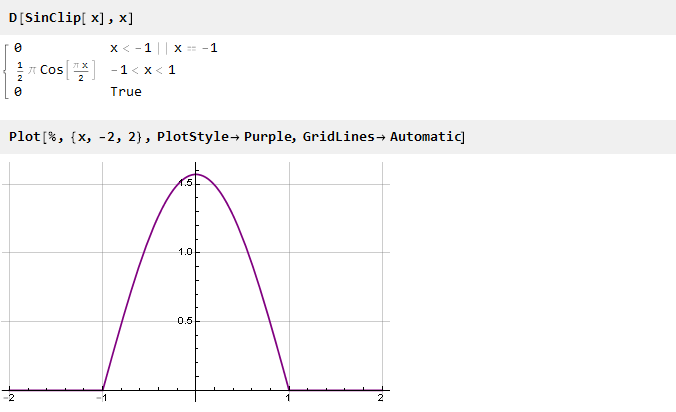
Il n'y a plus de lacunes dans les valeurs, mais il y a des lacunes dans la dérivée (la seconde, si l'on compte à partir de la fonction d'origine). Pour l'éliminer, vous pouvez procéder dans le sens inverse - former d'abord un dérivé lisse, puis l'intégrer pour obtenir la fonction souhaitée.
La façon la plus simple d'annuler la dérivée aux points -1 et 1 est de simplement mettre la fonction au carré - toutes les valeurs négatives de la fonction deviendront positives et, en conséquence, les inflexions se produiront aux points d'intersection de la fonction avec zéro.
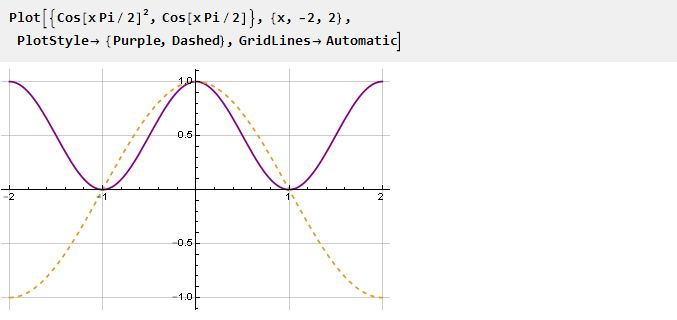
Trouvez l'antidérivatif:
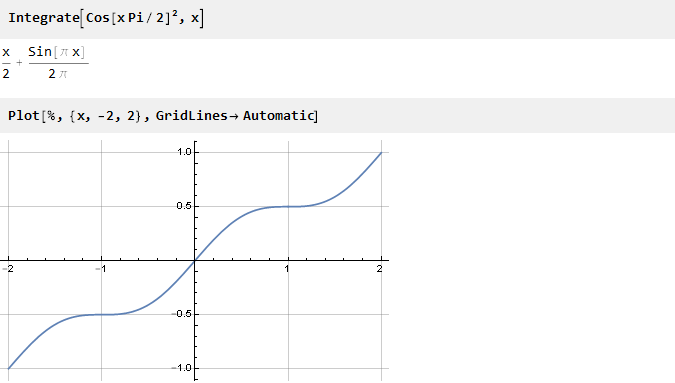
Il reste maintenant à le mettre à l'échelle le long de l'axe des ordonnées. Pour ce faire, trouvez sa valeur au point 1:

Et divisez-le (oui, spécifiquement ici c'est une multiplication élémentaire par 2, mais cela ne se produit pas toujours):

Ainsi, la fonction de restriction finale prendra la forme:
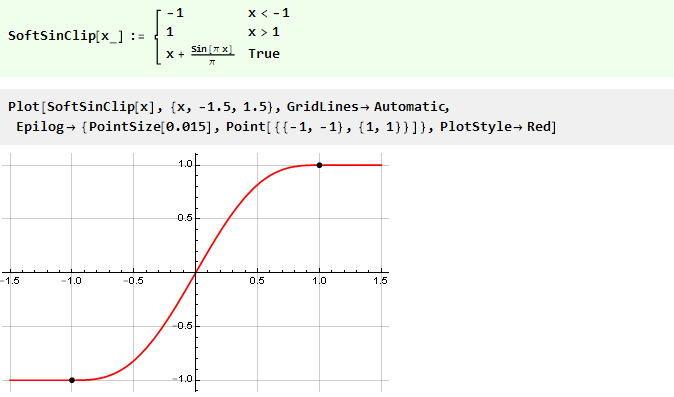
Nous passons aux polynômes
L'utilisation de fonctions trigonométriques dans certains cas peut être quelque peu inutile. Par conséquent, nous allons essayer de construire la fonction dont nous avons besoin, en restant dans le cadre des opérations mathématiques élémentaires.
Considérez la parabole:
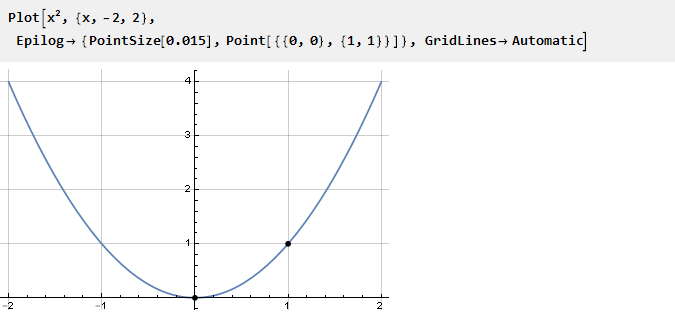
Puisqu'il a déjà une flexion au point zéro, nous pouvons utiliser la même partie sur l'intervalle {0,1} pour l'ancrage avec des constantes. Pour les valeurs négatives, il doit être déplacé vers le bas et vers la gauche:

et pour positif - réfléchir verticalement et horizontalement:

Et notre fonction avec une parabole prendra la forme:
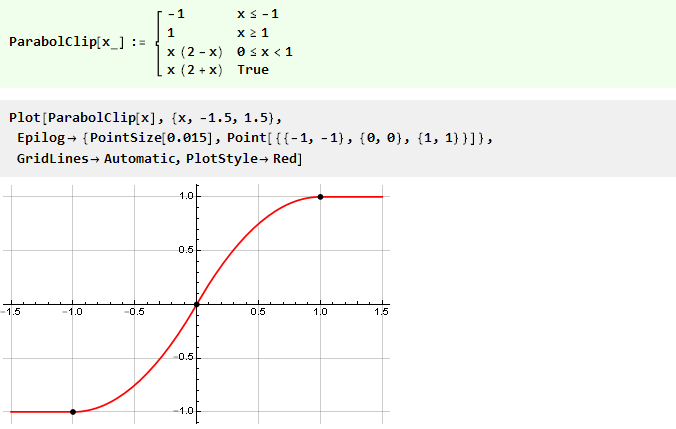
Compliquons un peu
Revenons à notre parabole, retournons-la et remontons d'une unité:
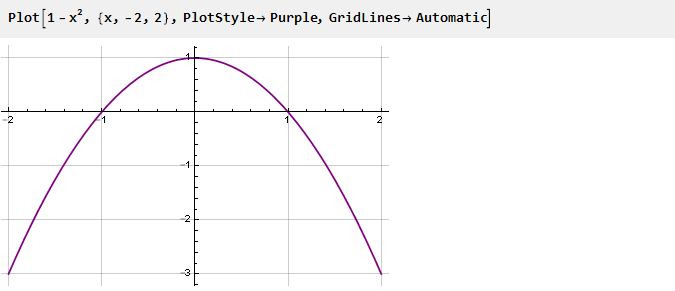
Ce sera un dérivé de notre fonction. Pour le rendre plus lisse aux points de jonction, nous allons quadriller, en mettant à zéro la dérivée seconde de cette manière:
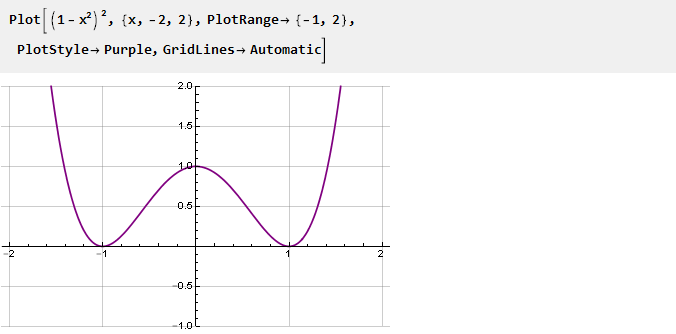
Intégrer et évoluer:

Nous obtenons une fonction encore plus fluide:
Plus de douceur au dieu de la douceur
Ici, nous essayons d'obtenir une fluidité aux points d'ancrage sur des dérivés encore plus élevés. Pour ce faire, pour commencer, nous définissons la fonction comme un polynôme avec des coefficients inconnus, et essayons de trouver les coefficients à travers une solution du système d'équations.
Commençons par la 1ère dérivée:

2e:

3ème:

Tous ces coefficients semblent avoir une sorte de logique. Nous écrivons les facteurs en les multipliant par la valeur du degré en x; et afin de ne pas écrire la même chose à chaque fois, nous automatisons le processus de recherche des coefficients:
 Cela ressemble à des
Cela ressemble à des coefficients binomiaux. Nous faisons l'hypothèse audacieuse qu'ils le sont, et sur la base de cela, nous écrivons la formule généralisée:

Vérifier:
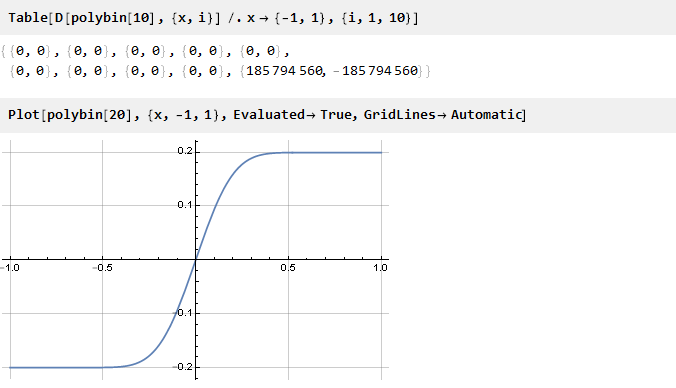
Cela semble être vrai
[1] . Il ne reste plus qu'à calculer le facteur d'échelle pour amener les bords à l'unité:

Et après mise à l'échelle et simplification, nous constatons que nos connaissances en mathématiques sont quelque peu dépassées
[2] :
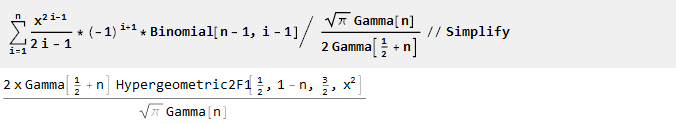
Ainsi, nous avons obtenu une fonction génératrice d'ordre n dans laquelle n-1 des premières dérivées sont égales à zéro:

Voyons ce qui s'est passé:
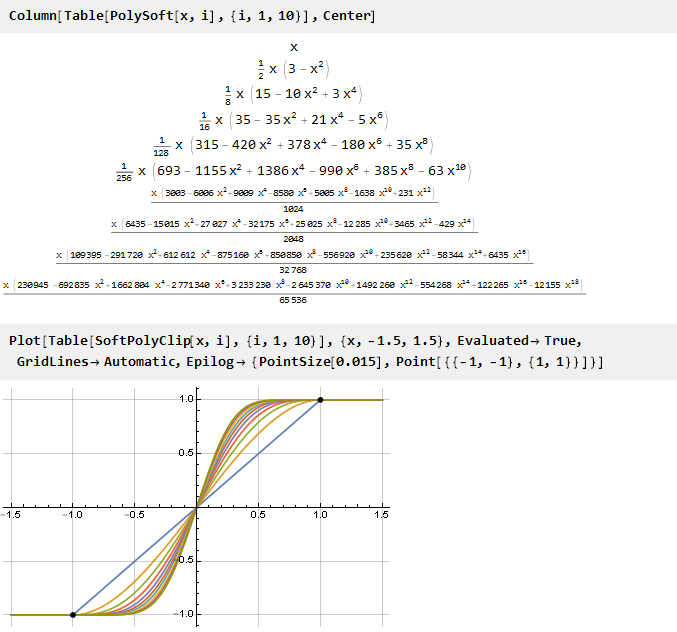
Et puisque notre formule généralisée s'est avérée être continue, vous pouvez utiliser des valeurs de paramètre non entières si vous le souhaitez:
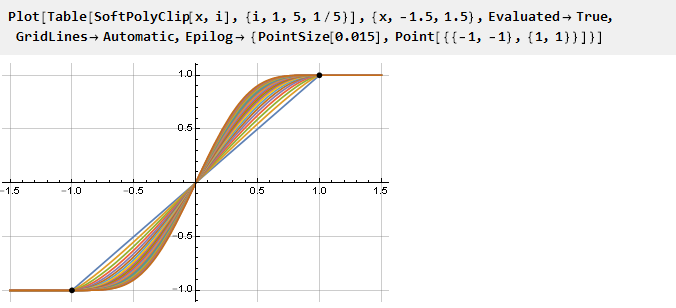
Vous pouvez également créer des graphiques de dérivés réduits à une échelle:
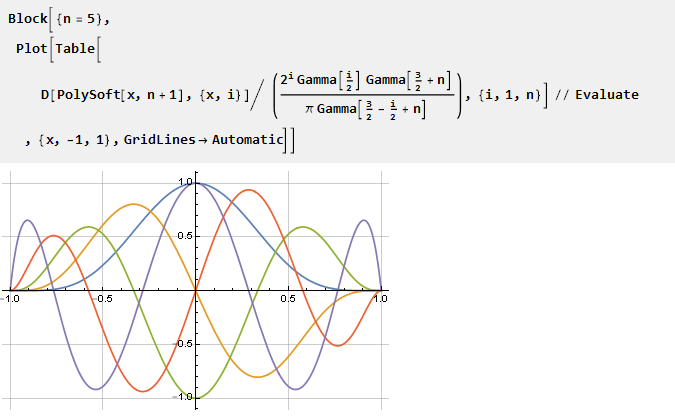
Ajouter de la rigidité
Il serait tentant de pouvoir ajuster le degré de «rigidité» de la restriction.
Revenons à notre parabole inversée et ajoutons un coefficient au degré x:

Plus n est grand, plus notre dérivée est «carrée», et son antérivative est nette, respectivement:
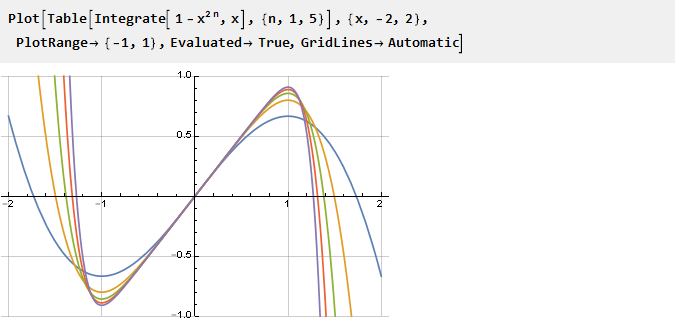
Nous calculons l'antidérivatif et ajustons l'échelle:

Essayons maintenant de définir le pas fractionnaire pour le paramètre:
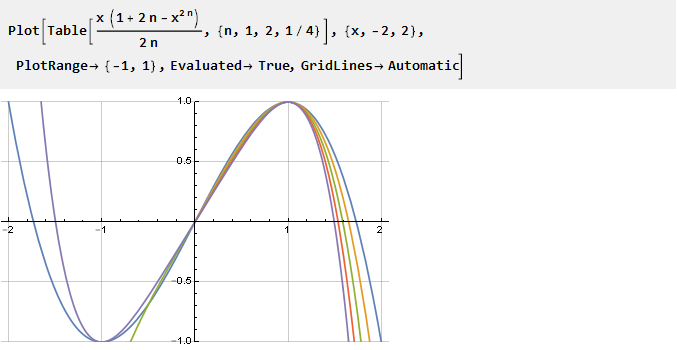
Comme vous pouvez le voir, tous les n n'ont pas la bonne solution dans la partie négative, mais les conditions nécessaires pour nous sont toujours remplies dans la partie droite (positive) - par conséquent, pour les valeurs négatives, nous pouvons simplement l'utiliser inversé avec un argument inversé. Et comme le domaine de définition du paramètre ne se limite plus uniquement aux entiers positifs, on peut simplifier la formule en remplaçant 2n par n:

Et en remplaçant n par n-1, vous pouvez rendre la formule un peu plus belle:
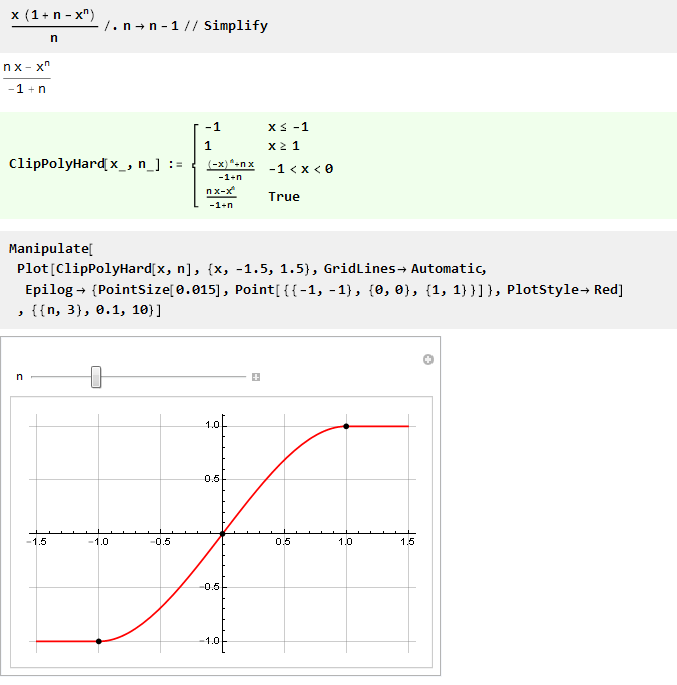
Puisque pour n égal à un, nous obtenons une division par zéro, alors essayons de trouver la limite:

La limite est trouvée, ce qui signifie que maintenant nous pouvons ajouter
[3] la fonction pour n à 1 et la considérer pour tous les n gros zéros:
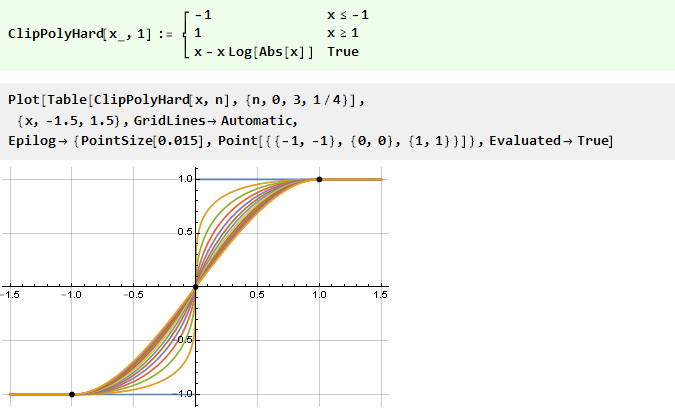
Si nous ajustons initialement notre parabole inversée, nous obtenons une fonction encore plus fluide:
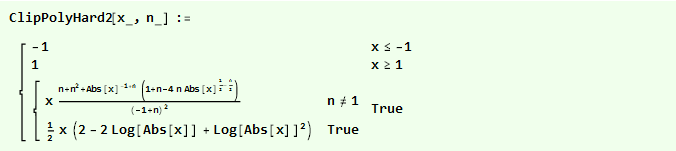
Et nous pouvons les comparer sur un seul graphique:
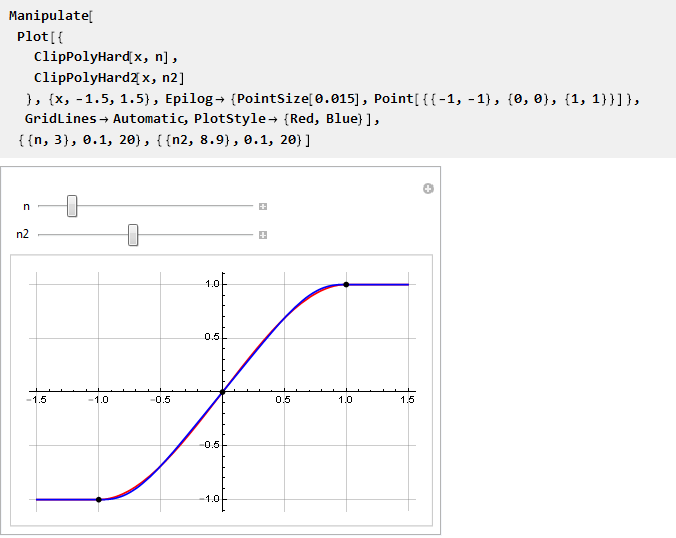
Rationalisez-le
Regardons la fonction suivante:
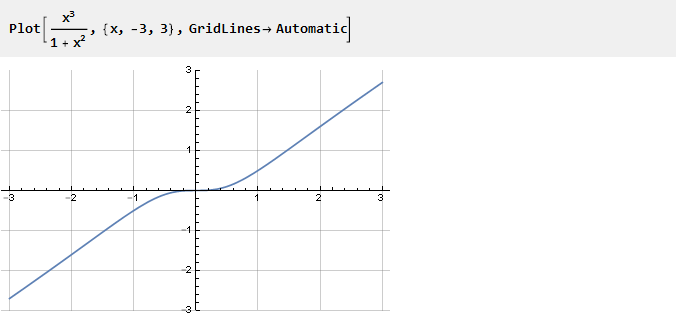
Elle n'est pas apparue par hasard.
Si vous en retirez une unité, x
2 se contractera et il ne restera que x, c'est-à-dire une ligne inclinée. Ainsi, plus la valeur de x est petite, plus l'influence de l'unité dans le dénominateur est grande, créant la courbure dont nous avons besoin. Et compte tenu de cette fonction à différentes échelles, vous pouvez contrôler le degré de cette courbure:

Ainsi, nous pouvons réécrire la fonction précédente avec un contrôle de rigidité en utilisant uniquement un polynôme rationnel de 3 ordres:
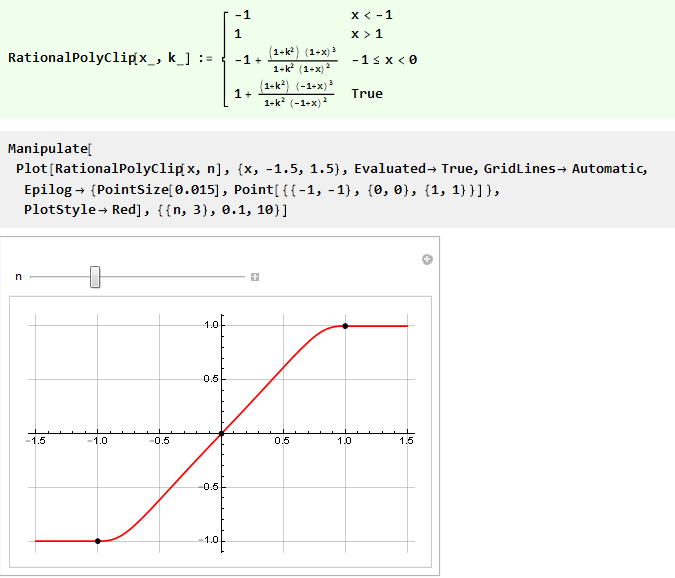
Automatisez-le
Afin de ne pas spécifier à chaque fois des fonctions continues par morceaux, nous pouvons définir une fonction auxiliaire qui le fera seule, en prenant une fonction donneur comme argument en entrée.
Si notre fonction a déjà une symétrie diagonale et est alignée sur le centre des coordonnées (comme une onde sinusoïdale), alors nous pouvons simplement faire
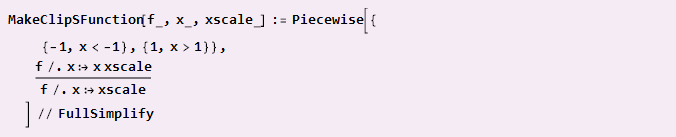
Exemple d'utilisation:

Si vous devez assembler à partir de pièces, comme dans le cas d'une parabole, et que le centre des coordonnées détermine les points d'ancrage, la formule sera légèrement plus compliquée:
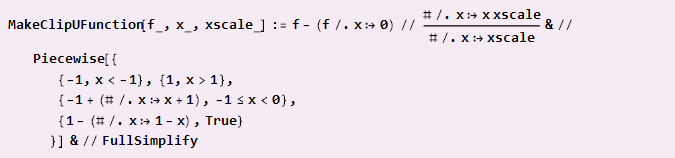
Exemple d'utilisation:

Passons à l'exposant
Absolument n'importe quelle fonction peut être un donateur pour résoudre ce problème, il vous suffit de lui fournir des points d'inflexion. Prenons, par exemple, l'exposant décalé d'une unité:
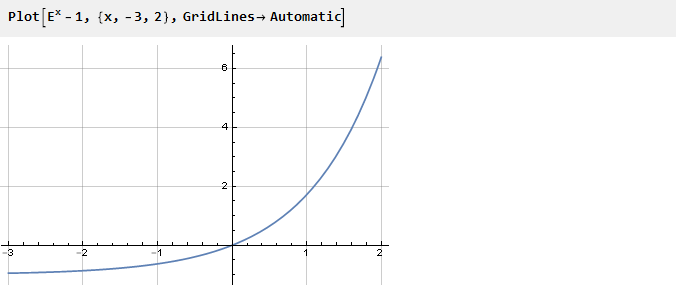
Auparavant, pour assurer l'inflexion nécessaire au point zéro, nous avons quadrillé la fonction. Mais vous pouvez aller dans l'autre sens - par exemple, résumer avec une autre fonction dont la dérivée au point zéro est de signe opposé à la dérivée de l'exposant. Par exemple, -x:
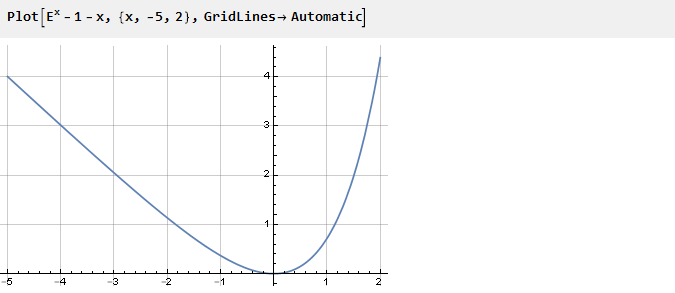
Selon de quel côté nous prendrons la courbe, la forme finale de la fonction en dépendra. Maintenant, en utilisant la fonction auxiliaire précédemment définie et en choisissant l'un des côtés, nous obtenons:

Soit

Et maintenant, nous pouvons les comparer sur un seul graphique:
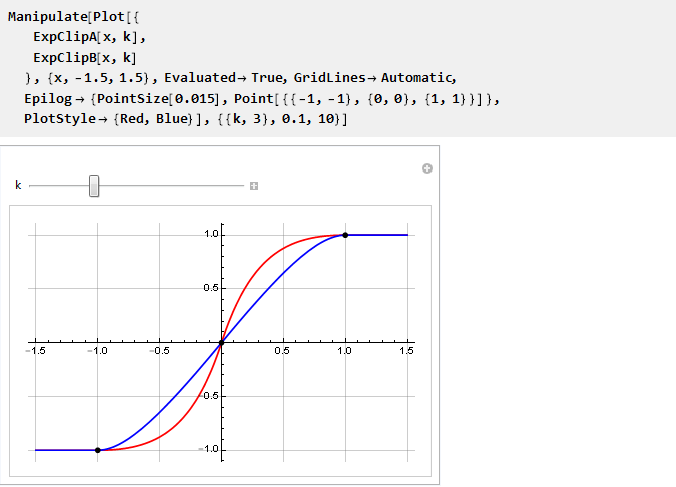
On voit que lorsque k → 0 ils ont tendance à coïncider; et puisque nous ne pouvons pas calculer directement leurs valeurs, puisque nous obtenons une division par zéro, nous utiliserons la limite:

Et ils ont obtenu la fonction par morceaux de la parabole que nous connaissons déjà.
Briser la symétrie
Jusqu'à présent, nous avons envisagé des fonctions exclusivement symétriques. Cependant, il y a des moments où nous n'avons pas besoin de symétrie - par exemple, pour simuler des distorsions dans le son des amplificateurs à lampes.
Prenez l'exposant et multipliez-le par la parabole inversée au carré - pour obtenir l'intersection avec l'axe des abscisses aux points -1 et 1, et en même temps assurer la régularité de la dérivée seconde; le paramétrage est possible grâce à la mise à l'échelle de l'argument exposant:
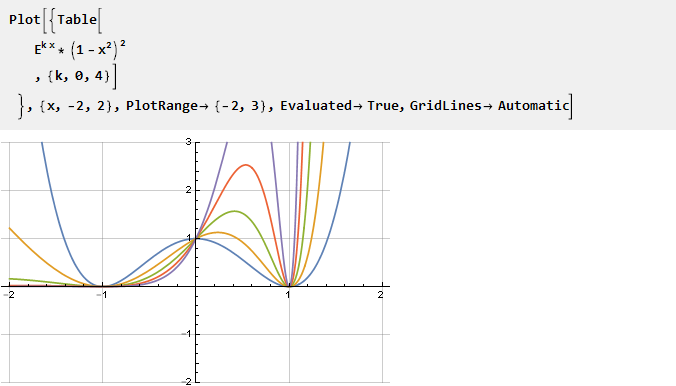
Trouvez l'antidérivatif et mettez-le à l'échelle:
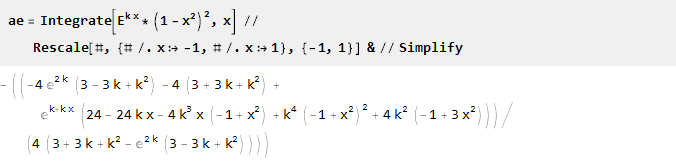
Puisque pour k = 0 on obtient la division par zéro:

Ensuite, nous trouvons également la limite,

qui est un polynôme lisse du troisième ordre que nous connaissons déjà. En combinant tout en une seule fonction, nous obtenons
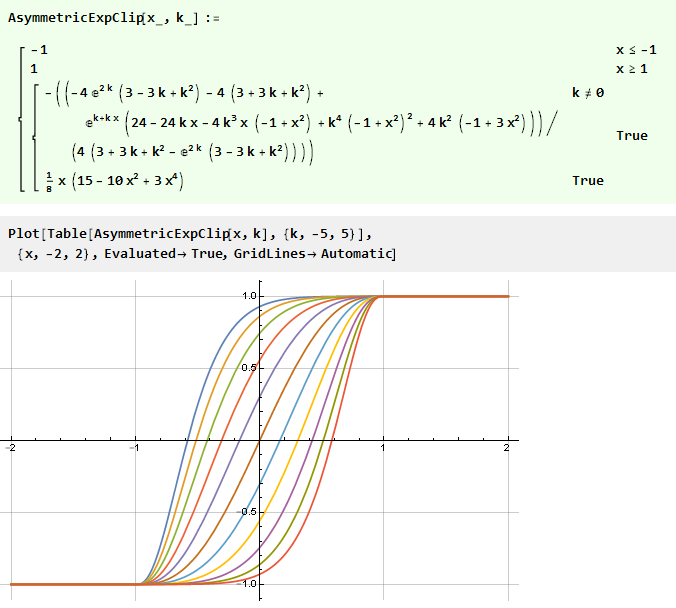
Au lieu de concevoir initialement une fonction asymétrique, vous pouvez aller dans l'autre sens - utilisez la symétrie prête à l'emploi, mais «pliez» la valeur de cette fonction en utilisant une fonction de courbe supplémentaire définie sur l'intervalle {-1,1}.
Prenons, par exemple, une hyperbole:
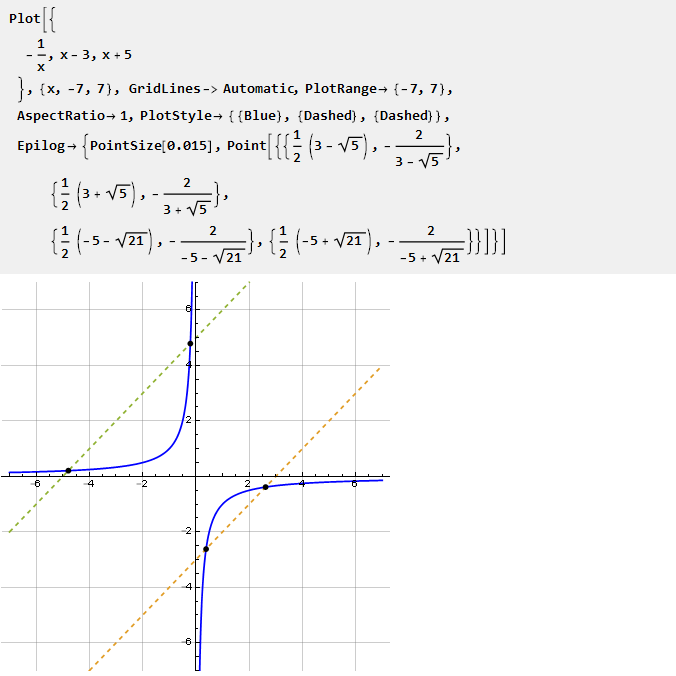
Compte tenu de son segment à différentes échelles, vous pouvez ajuster le degré de courbure dans les deux directions. Comment trouver ce segment? Sur la base du graphique, on pourrait rechercher l'intersection de l'hyperbole avec la ligne. Cependant, comme une telle intersection n'existe pas toujours, cela crée des difficultés. Par conséquent, nous irons dans l'autre sens.
Tout d'abord, ajoutez des facteurs d'échelle à l'hyperbole:

puis nous composerons un système d'équations définissant les conditions pour qu'une hyperbole passe par des points donnés - et sa solution nous donnera les coefficients qui nous intéressent:

Remplacez maintenant la solution dans la formule d'origine et simplifiez:

Voyons ce que nous obtenons, en fonction du paramètre k:
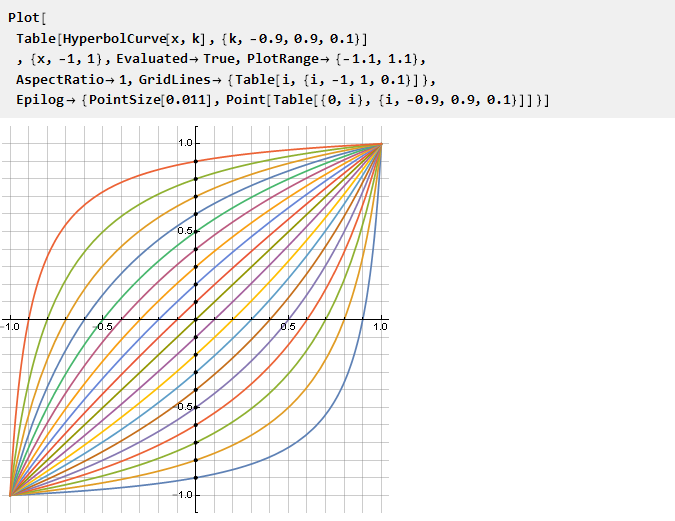
Il est à noter que pour k = 0, la formule s'effondre naturellement en x et qu'aucune situation particulière ne se produit - bien qu'en référence à l'hyperbole initiale, cela équivaut à un segment de longueur nulle, et deux à la fois. Il est non moins remarquable que la fonction inverse à celle-ci soit la même, mais avec un paramètre négatif k:

Maintenant, nous pouvons l'utiliser pour modifier une fonction de contrainte arbitraire, et le paramètre k définit donc le point d'intersection avec l'axe des ordonnées:
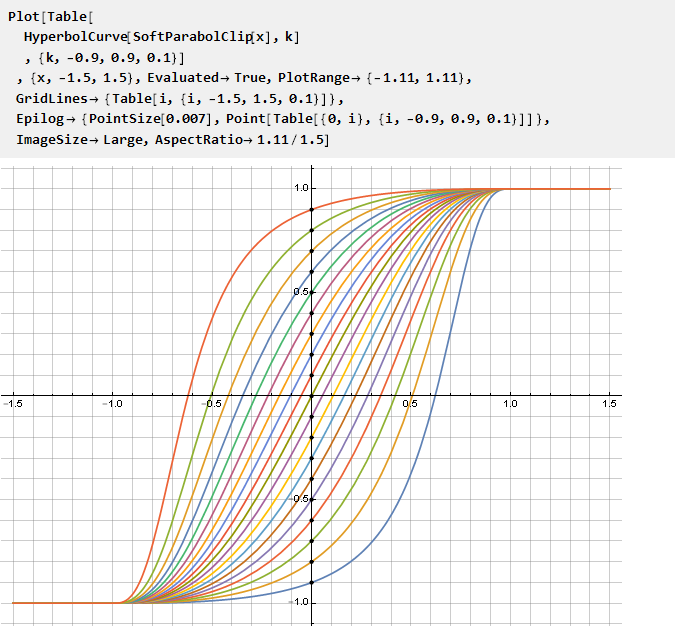
De même, vous pouvez créer des courbes à partir d'autres fonctions, par exemple, une loi de puissance avec une base variable:
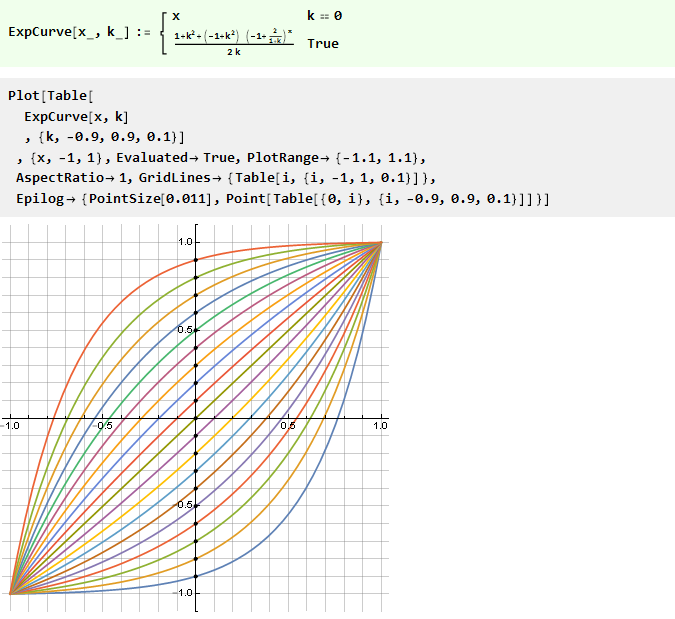
Ou l'inverse est logarithmique:
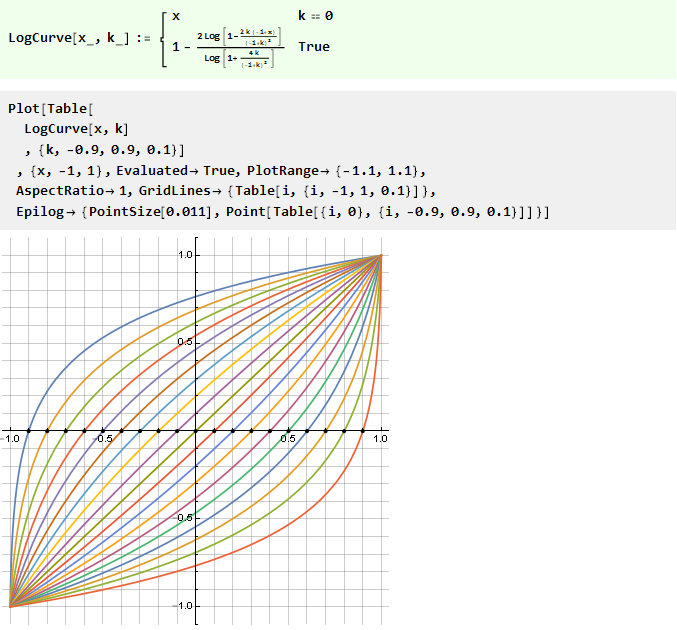
Besoin de plus de précision
Nous pouvons vouloir avoir un espacement linéaire garanti pour une fonction sur un certain intervalle. Il est logique d'organiser en introduisant une ligne droite dans une fonction continue par morceaux,
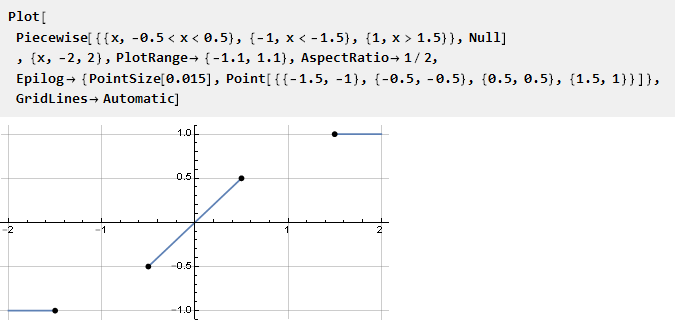
espaces vides dans lesquels vous devez remplir une fonction. Évidemment, pour un amarrage lisse avec une section linéaire, sa première dérivée doit être égale à l'unité; et tous les zéros suivants (si possible). Afin de ne pas déduire une telle fonction à nouveau, nous pouvons prendre une fonction toute faite et l'adapter à cette tâche. Vous pouvez également remarquer que les points extrêmes sont situés un peu plus loin que l'unité - cela est nécessaire pour maintenir la pente de la section linéaire.
Prenez la fonction PolySoft précédemment dérivée et déplacez-la pour que nous en obtenions une au centre des coordonnées:
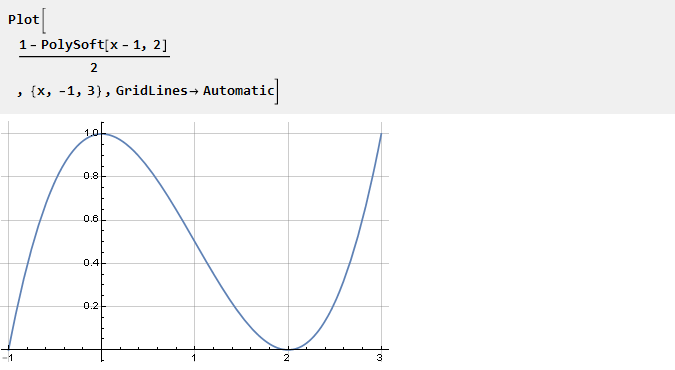
De ses propriétés, il résulte que n-1 des dérivées suivantes aux points 0 et 2 sera égal à zéro:
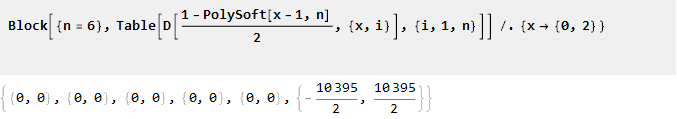
Maintenant, intégrez-le:
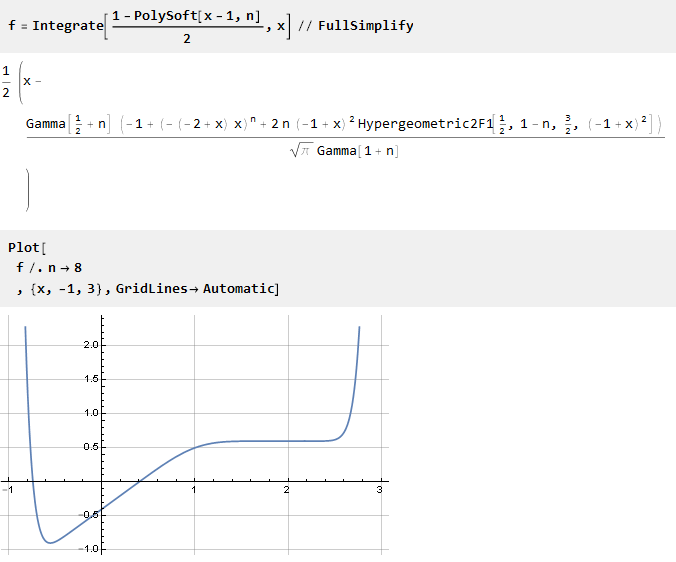
La fonction a été décalée vers le bas par rapport à l'axe des abscisses. Par conséquent, il est nécessaire d'ajouter une constante (égale à la valeur de la fonction au point 0) afin de combiner les centres de coordonnées:

Ici, nous avons zéro en degré n. Il n'a pas diminué, car la valeur de zéro dans le degré de zéro n'est pas définie; on peut le supprimer manuellement, ou, en simplification, on peut explicitement indiquer que n est supérieur à zéro:

Nous vérifierons au cas où. La valeur aux points 0 et 2 pour tout n:

Dérivés aux bords de l'intervalle (pour un polynôme d'ordre 5):

Comme vous pouvez le voir, la fonction s'est avérée assez lourde. Afin de ne pas le faire glisser et de ne pas compliquer les calculs, nous continuerons à manipuler avec un polynôme spécifique, par exemple de 4ème ordre:

Et maintenant, avec lui, vous pouvez remplir l'espace libre:

Vérifier:
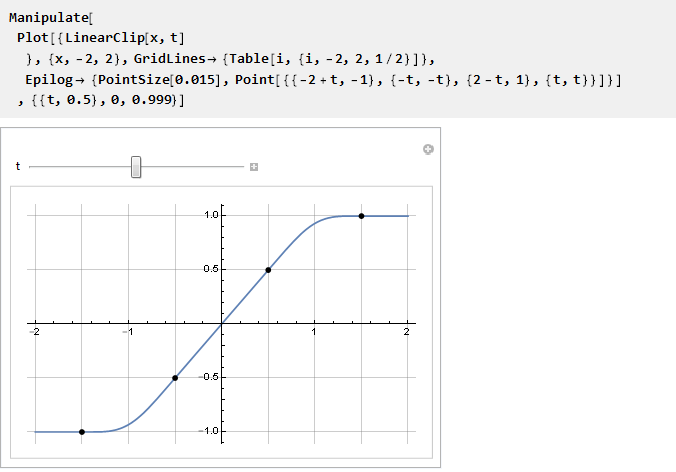
On va à l'infini
Parfois, il peut y avoir un besoin de fonctions qui tendent vers une unité mais ne l'atteignent pas. Wikipedia
propose plusieurs solutions bien connues:
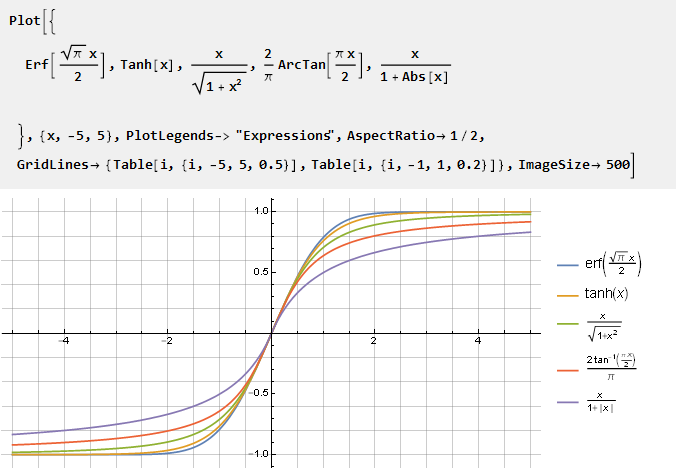
Comme ces fonctions n'atteignent pas l'unité, il est plus pratique de les normaliser par rapport à la dérivée au centre des coordonnées.
Nous pouvons modifier la forme de ces fonctions grâce à leur argument en utilisant une fonction diagonale symétrique, par exemple:
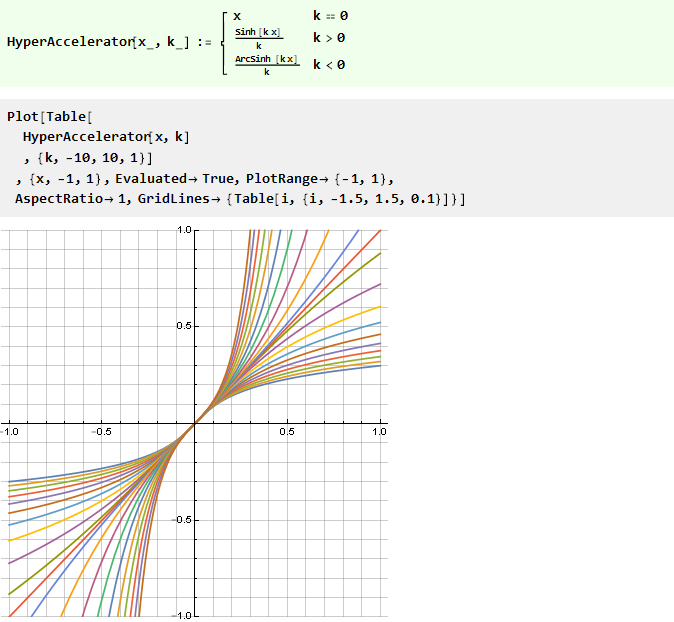
Cette fonction, soit dit en passant, est également inverse d'elle-même, c'est-à-dire
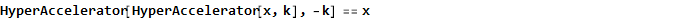
Et, comme appliqué à l'arctangente, par exemple, nous obtenons
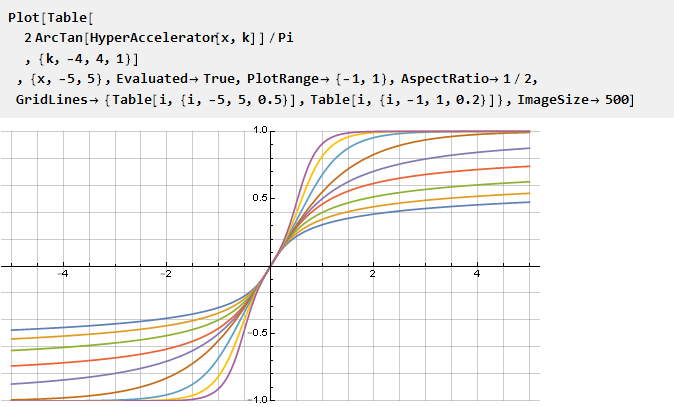
qui, en particulier, avec le paramètre k = 1 nous donnera
la fonction de Guderman .
Comme vous pouvez le voir, avec cette approche, des plis indésirables peuvent être obtenus, il est donc plus préférable de contrôler la rigidité de la contrainte directement via la propriété de la fonction elle-même. Considérez plusieurs de ces fonctions avec un paramètre, dont la sortie est omise par souci de concision.
De la fonction de puissance:
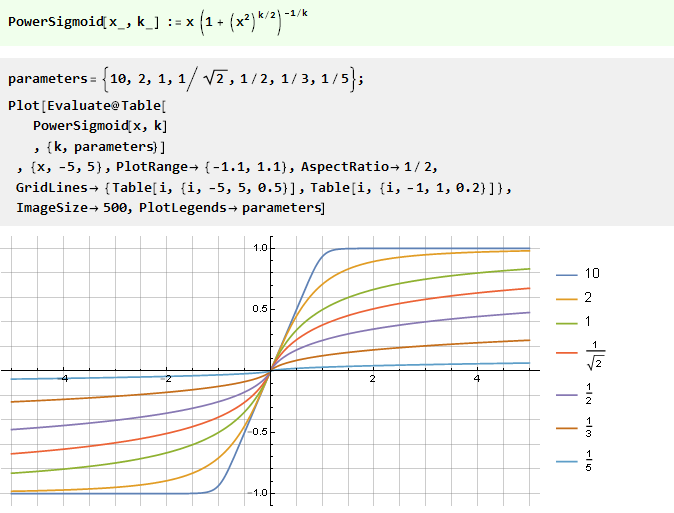
De la somme de deux fonctions en forme de V avec un décalage:
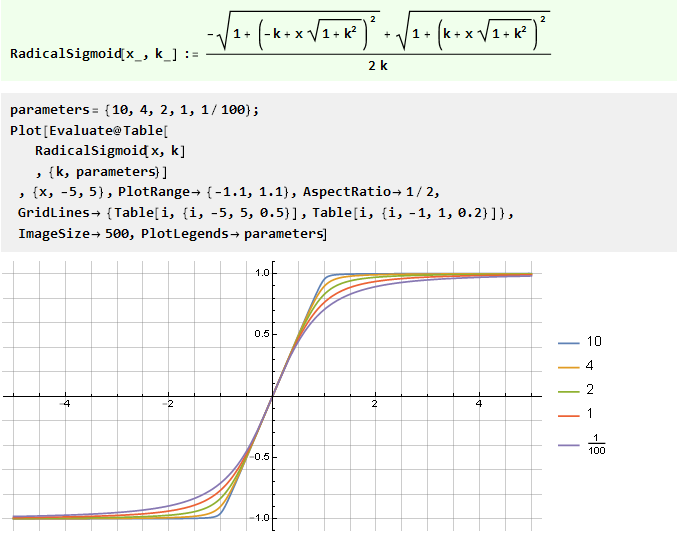
De la fonction d'erreur généralisée:
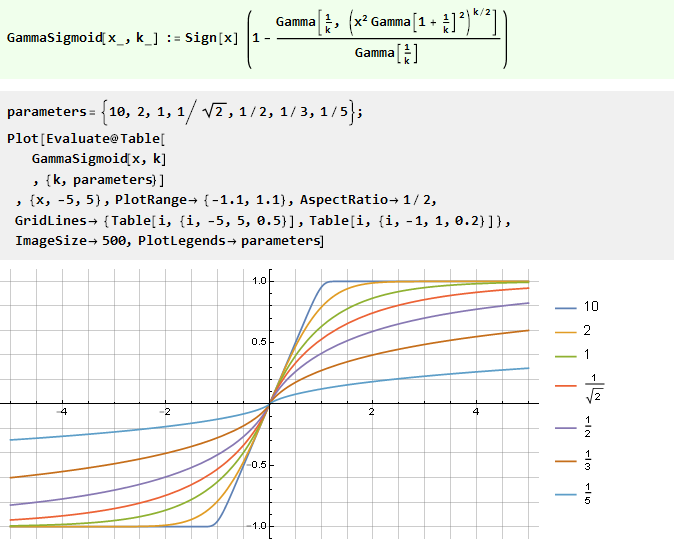
Intégration d'un polynôme rationnel:
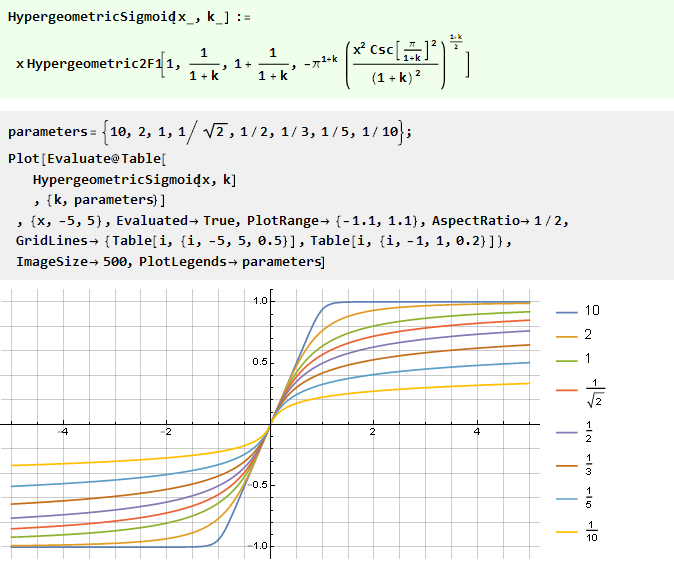
Fait intéressant, son cas particulier est arctangent:

Conclusion
La construction de telles fonctions peut être une tâche fascinante, au cours de laquelle des formules à la fois simples et complexes, à la fois belles et peu nombreuses seront obtenues. Il peut sembler qu'ils sont tous très similaires les uns aux autres et il n'y a pas besoin d'une telle variété. Ce n'est pas nécessairement le cas.
La différence peut être plus visible à d'autres échelles - par exemple, logarithmique. De plus, en plus des tâches indiquées dans l'en-tête, des fonctions similaires peuvent être utilisées dans d'autres tâches - mélanger des signaux, lorsque l'atténuation douce d'un signal est combinée avec une augmentation douce d'un autre, ou la construction de filtres acoustiques - et ensuite la différence sera perçue à l'oreille ou pour construire des gradients - puis la différence sera perçue à l'œil. En outre, ils peuvent également être utilisés comme donateurs pour d'autres fonctions plus complexes - par exemple, la
fenêtre .
En conclusion, il convient de clarifier quelques points supplémentaires.
Toutes les fonctions ici ont été définies dans la plage de -1 à 1. Si vous avez besoin d'une plage différente (par exemple, de 0 à 1), elle peut être facilement recomptée manuellement:
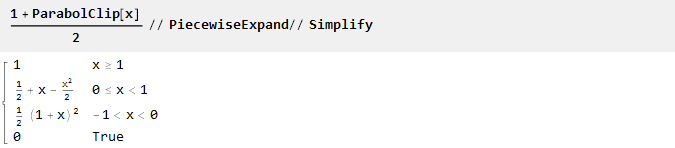
Ou en utilisant la fonction de zoom intégrée:

Et pour faciliter l'exportation des formules obtenues vers le code programme, la fonction CForm peut être utile:
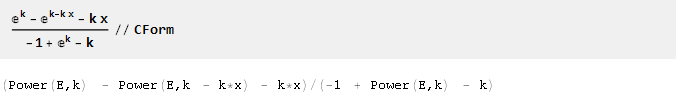
Le document source de Mathematica peut être téléchargé
ici .
Remarques:
[1] Un vrai mathématicien pourra certainement prouver (ou réfuter) rigoureusement cette affirmation.
[2] les fonctions hypergéométriques ne sont pas prises en compte dans le cours standard de l'analyse mathématique.
[3] cette surcharge n'est définie que pour une unité de caractères; une unité au format virgule flottante (par exemple, lors du traçage d'un graphique) ne sera pas reconnue.