L'examen de la structure des amitiés existantes dans votre environnement peut vous aider à mieux créer de nouvelles relations tout en créant un nouveau cercle d'amis.
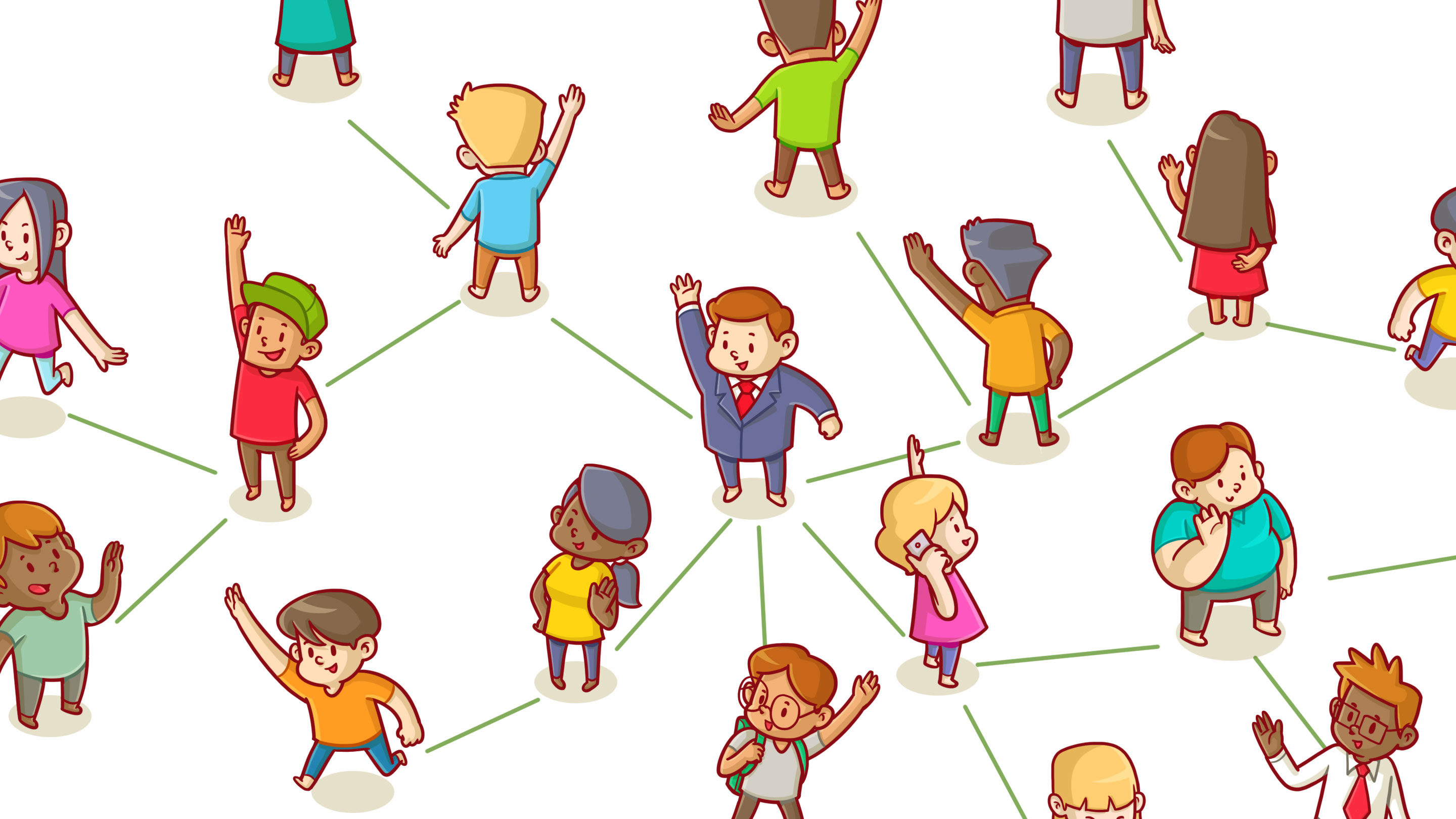
Déménager dans une nouvelle école, un nouvel emploi, déménager dans une nouvelle ville - comment se faire de nouveaux amis? Vous pouvez aborder le problème activement, former des relations stratégiquement utiles avec des gars populaires. Ou vous pouvez tout laisser au hasard, en vous appuyant sur des groupes et des connexions aléatoires. Dans toute approche, la compréhension de la structure des amitiés existantes dans un nouvel environnement peut vous aider à former les meilleures nouvelles relations, qui détermineront finalement votre cercle de connaissances.
Imaginez que vous déménagiez dans une nouvelle ville inhabituelle, Regularsk, dans laquelle il existe une règle étrange: chaque personne ne peut pas avoir plus de quatre amis, mais tout le monde veut maximiser le nombre de ses connexions. À quoi ressemblera la structure des obligations Regularsk? Pour étudier cette question, nous utilisons un objet mathématique appelé réseau.
En termes simples, un réseau est une collection d'objets appelés «nœuds» et les connexions entre eux. Les réseaux sont un concept mathématiquement flexible. Ils peuvent désigner les ordinateurs et les câbles qui les relient, les auteurs et leurs assistants, les états du cube de Rubik et les transformations qui permettent la transition entre eux - en fait, tout type de connexions, réelles ou abstraites. Pour étudier les amitiés à Regularsk, nous allons créer un réseau dans lequel les gens seront des nœuds et des amitiés entre eux.
En désignant le réseau, il sera utile de représenter les nœuds sous forme de points, et les connexions sous forme de lignes, que nous pouvons également appeler bords. Un tel schéma de réseau peut nous aider à comprendre sa structure. À quoi ressemblera le réseau d'amitié Regularsk? À un moment donné, cela peut ressembler à ceci:

Chaque personne tentera de trouver quatre amis, et les nouvelles personnes qui viendront en ville chercheront celles qui ont encore moins de quatre amis. Ce réseau se développera au fil du temps et se développera constamment avec l'ajout de nouveaux nœuds. (Il est possible de former des groupes indépendants, mais dans cet exemple, nous les négligeons).
Les diagrammes de réseau peuvent aider à les comprendre, montrant une structure claire. Mais lorsque les réseaux se développent ou ne présentent pas une structure aussi régulière que le réseau régulier, les diagrammes peuvent devenir moins utiles. Dans ce cas, il est utile de développer différentes méthodes d'analyse de la structure du réseau. L'un d'eux est d'évaluer la distribution des degrés de sommets.
Dans un réseau, le nombre de liens d'un nœud particulier est appelé son degré. Un nœud est fortement associé à de nombreux autres; un nœud de faible degré est associé à moins d'autres nœuds.
 A gauche - un nœud avec un degré de 8, à droite - avec un degré de 3
A gauche - un nœud avec un degré de 8, à droite - avec un degré de 3Le degré de nœuds est une caractéristique importante du réseau, mais local: il ne décrit la structure du réseau qu'à l'intérieur d'un seul nœud. Mais si vous couvrez les degrés de tous les nœuds à la fois, vous pouvez créer un outil utile pour étudier la structure du réseau global.
Dans notre réseau d'amis, le degré de chaque nœud est le nombre d'amis d'une personne. À Regularsk, la plupart des gens ont quatre amis, donc la plupart des nœuds ont un degré de 4. Personne n'aura plus d'amis, mais quelqu'un en aura moins, donc il y aura des nœuds avec des degrés 3, 2 ou 1. Vous pouvez résumer la distribution des degrés comme suit:

Cet histogramme transmet des informations importantes sur la structure de notre réseau. Dans cet exemple simple, il peut ne pas nous transmettre autant qu'un diagramme de réseau complet, mais nous verrons comment la distribution des degrés peut être très utile pour étudier divers réseaux.
Passons à une autre ville. Dans un gâchis, la datation commence au hasard. Puisque le hasard est une chose délicate, décrivons clairement la portée: chaque résident de la ville est désigné par un nœud de réseau, et chaque bord possible est une connexion conviviale. Pour créer une connexion aléatoire, nous allons choisir l'une de ces arêtes possibles de manière aléatoire, et la dessiner, créant ainsi une connexion entre deux nœuds, et donc une amitié entre deux personnes.
À quoi ressemblera le réseau de mess? Si nous supposons que nous avons commencé avec plusieurs nœuds et ajouté plusieurs bords au hasard, l'image peut être la suivante:

Dans un tel diagramme, il est difficile de voir la structure. Cependant, beaucoup nous dira la répartition des diplômes dans ce réseau. Il est difficile à calculer directement, mais peut être représenté à l'aide de plusieurs propriétés importantes et d'un exemple simple.
Supposons que vous soyez l'un des dix résidents du mess. Combien d'amitiés probables peuvent y exister? Chacun des dix résidents peut être associé à neuf autres, donc, en principe, il est possible de dessiner 10 × 9 = 90 bords. Mais un tel calcul prend en compte chaque connexion deux fois - une fois pour chacun des deux amis. Par conséquent, en fait, le nombre total d'obligations devrait être de 90/2 = 45.
Maintenant, disons que nous choisissons au hasard une relation amicale - c'est-à-dire l'un des 45 bords possibles. Quelle est la probabilité que la côte se connecte avec vous? Neuf arêtes peuvent vous laisser sur l'un des neuf nœuds restants. Étant donné que neuf arêtes possibles sur 45 vous conduisent, la probabilité qu'une arête sélectionnée au hasard se connecte à vous est de 9/45 = 1/5, ou 20%.
Mais le même argument s'applique à Disorder, donc chaque nœud aura 20% de chances de se connecter à un bord sélectionné au hasard. Avec une augmentation du nombre d'arêtes et de nœuds, ces probabilités changeront légèrement, mais à long terme, elles resteront approximativement au même niveau. Autrement dit, les amitiés seront réparties à peu près également dans le mess. Dans certains endroits, de petits écarts seront observés, mais la probabilité qu'une personne ait trop ou trop peu d'amitiés sera faible. Dans le trouble, la plupart des résidents auront probablement des amis proches avec des amis moyens.
Ces caractéristiques concernent la «
distribution binomiale » des degrés d'un réseau aléatoire typique.

N'ayant accès qu'à la distribution des degrés dans le réseau, on peut déjà y trouver une certaine uniformité: la plupart des nœuds en termes de connectivité sont moyens, et un très petit nombre de nœuds sont en position extrême. Ces informations sont utiles pour comprendre la structure du réseau. Avec l'ajout de nœuds, c'est-à-dire avec l'arrivée de nouvelles personnes dans la ville, la distribution changera légèrement, tout en conservant les principales caractéristiques.
Mais aucun de ces exemples - pas plus de quatre amis à Regularsk ou une amitié apparaissant au hasard dans Disorder - n'est un modèle réaliste de liens d'amitié. Les gens peuvent avoir plus de quatre amis et la présence d'un grand nombre de connaissances n'est pas du tout aussi rare que dans la distribution binomiale. Quel sera un modèle d'amitié plus réaliste?
Lorsque vous établissez des liens avec des amis et des amis d'amis, la structure de vos amitiés ressemblera très probablement à d'autres
réseaux du monde réel -
réseaux alimentaires ,
interactions protéine-protéine ou Internet. Leurs propriétés caractérisent les
réseaux dits
sans échelle - un tel modèle de connectivité domine la science des réseaux depuis plus de 20 ans. Des chercheurs en mathématiques, physique, économie, biologie et sciences sociales ont observé des signes caractéristiques de la présence de réseaux sans échelle dans leurs domaines de recherche.
 Réseau de mise en réseau social sophistiqué sans évolutivité
Réseau de mise en réseau social sophistiqué sans évolutivitéLa structure d'un réseau sans échelle dépend du principe simple des «connexions préférées». La connexion préférée est la règle «riche devient riche», qui fait référence à la croissance du réseau. Un nœud avec un grand nombre de connexions existantes est beaucoup plus susceptible d'obtenir de nouvelles connexions qu'un nœud avec un petit nombre. Les nouvelles connexions montrent une tendance vers des nœuds avec un grand nombre de connexions.
Cela a-t-il un sens dans le contexte de la formation d'amitiés? En principe, il est raisonnable de supposer qu'une personne avec plus d'amis est plus susceptible d'en faire de nouveaux. Puisqu'il est déjà associé à un grand nombre de personnes, la probabilité de rencontrer de nouvelles personnes en raison des connexions existantes est élevée. Plus il y a d'amis, plus il y a d'occasions de se faire de nouveaux amis. Et le fait qu'ils aient déjà beaucoup d'amis, dit qu'ils ont une sorte d'opportunité ou un penchant pour l'amitié. Cela est plus susceptible d'attirer d'autres personnes vers eux, tout comme les sites populaires attirent des liens depuis d'autres sites et blogs, et les villes développées créent de nouveaux chemins de fer et routes aériennes.
Bien que plusieurs facteurs influencent la croissance des réseaux sans évolutivité, beaucoup considèrent les connexions préférées comme les plus importantes. Il a également un effet étonnant sur la distribution des diplômes dans le réseau.

Il prédit l'apparition d'une distribution «à queue épaisse». La plupart des nœuds du réseau auront un petit degré, mais il y aura également des nœuds avec des degrés croissants. Ceci est très différent des réseaux amicaux Regularsk et Disorder, dans lesquels il y a très peu ou pas de nœuds avec de grands degrés.
Ces nœuds, à grande échelle, fonctionnent comme des concentrateurs de réseaux et sont une caractéristique essentielle des réseaux sans échelle. Ce sont des papillons sociaux dans les réseaux d'amis, des banques au centre des économies, des routeurs centralisés qui laissent passer les connexions Internet régionales,
Kevinov Beykonov dans le monde des acteurs . Les hubs peuvent donner l'impression d'un monde serré dans un vaste réseau - par exemple, deux personnes sélectionnées au hasard sur 2 milliards d'utilisateurs de Facebook ne sont en moyenne
pas plus éloignées l'une de l'autre
que dans quatre relations amicales . Le nombre et la variété des concentrateurs confèrent aux réseaux à grande échelle une résistance à un certain type de discontinuité. Par exemple, même avec l'échec de nombreuses connexions Internet, les messages seront toujours en mesure d'atteindre, en particulier parce qu'il y aura encore de nombreuses façons d'accéder à de nombreux concentrateurs vers de nombreux autres concentrateurs.
Et bien que beaucoup conviennent que les réseaux sans échelle et leurs propriétés sont utiles, il existe des contradictions dans ce domaine de recherche. Les caractéristiques mathématiques exactes d'une telle distribution des degrés sont parfois difficiles à interpréter. Dans Linked: The New Science of Networks, pionnier de la recherche sur les réseaux et physicien
Albert Lazlo Barabasi écrit que dans les réseaux montrant des connexions préférées, la distribution des degrés suivra une loi de puissance. Les distributions de puissance se retrouvent souvent dans de nombreuses situations physiques - par exemple, dans la loi des carrés inverses pour la gravité ou les champs électriques. Ils peuvent être représentés comme des fonctions ayant la forme
Leurs graphiques ressemblent généralement à ceci:

Les distributions de puissance ont des «queues épaisses». Mais quelle épaisseur? Combien de hubs d'un certain degré devraient être trouvés dans un tel réseau? Dans une
étude publiée cette année, plus de 1000 réseaux réels ont été étudiés, et il a été constaté que seulement un tiers d'entre eux peuvent avoir une distribution des degrés décrite par une loi de puissance. Pour de nombreux réseaux, la distribution des degrés pourrait être plus précisément décrite comme
exponentielle ou
log -
normale . Ils peuvent avoir des propriétés de haut niveau de réseaux sans échelle, mais peuvent-ils être considérés comme tels si leurs degrés ne sont pas distribués comme prévu? Et est-ce même important?
C'est important si nous voulons relier nos théories à nos données. La communication préférée est-elle un facteur majeur dans la construction de réseaux sans échelle? Y a-t-il d'autres facteurs qui jouent un rôle important et peuvent entraîner la distribution des diplômes de l'autre côté? En répondant à ces questions et en comprenant quelles questions devraient être posées ensuite, nous comprendrons vraiment mieux la nature et la structure des réseaux, comment ils se développent et évoluent.
Ces contradictions nous rappellent également que les mathématiques, comme les réseaux, sont également un ensemble de connexions en évolution. La recherche actuelle remet en question les hypothèses de 20 ans dans un domaine relativement nouveau de la recherche en réseau. De nouvelles idées, rejoignant le réseau, nous connectent tous avec les mathématiques du passé et du futur. Ainsi en matière mathématique, comme dans le domaine de l'amitié, il sera utile de trouver des hubs et de maximiser votre diplôme.
Exercices
- À quoi ressemblera un réseau d'amis si chaque personne a exactement deux amis?
- À Regularsk, chaque personne peut se faire jusqu'à quatre amis. Il peut exister des groupes distincts dans lesquels chaque personne a exactement quatre amis. Combien de personnes peuvent être incluses dans un tel groupe? (Indice: la réponse est liée aux polyèdres réguliers ).
- Nos réseaux sont basés sur le fait que l'amitié est un concept symétrique. Si A est ami avec B, alors B est ami avec A. Comment pouvons-nous corriger notre modèle de réseau afin qu'il puisse inclure des connexions asymétriques dans lesquelles A peut être ami avec B, et B ne peut pas être ami avec A?
- Dans Friends, chaque résident est ami avec tout le monde. S'il n'y a pas de personnes vivant dans Friends, combien y a-t-il de liens d'amitié?