Cours MIT "Sécurité des systèmes informatiques". Conférence 10: Exécution symbolique, partie 3

Institut de technologie du Massachusetts. Cours magistral # 6.858. "Sécurité des systèmes informatiques." Nikolai Zeldovich, James Mickens. 2014 année

Computer Systems Security est un cours sur le développement et la mise en œuvre de systèmes informatiques sécurisés. Les conférences couvrent les modèles de menace, les attaques qui compromettent la sécurité et les techniques de sécurité basées sur des travaux scientifiques récents. Les sujets incluent la sécurité du système d'exploitation (OS), les fonctionnalités, la gestion du flux d'informations, la sécurité des langues, les protocoles réseau, la sécurité matérielle et la sécurité des applications Web.

Cours 1: «Introduction: modèles de menace» Partie 1 / Partie 2 / Partie 3
Conférence 2: «Contrôle des attaques de pirates» Partie 1 / Partie 2 / Partie 3
Conférence 3: «Débordements de tampon: exploits et protection» Partie 1 / Partie 2 / Partie 3
Conférence 4: «Séparation des privilèges» Partie 1 / Partie 2 / Partie 3
Conférence 5: «D'où viennent les systèmes de sécurité?» Partie 1 / Partie 2
Conférence 6: «Opportunités» Partie 1 / Partie 2 / Partie 3
Conférence 7: «Native Client Sandbox» Partie 1 / Partie 2 / Partie 3
Conférence 8: «Modèle de sécurité réseau» Partie 1 / Partie 2 / Partie 3
Conférence 9: «Sécurité des applications Web», partie 1 / partie 2 / partie 3
Conférence 10: «Exécution symbolique» Partie 1 / Partie 2 / Partie 3

Maintenant, en suivant la branche vers le bas, nous voyons l'expression t = y. Puisque nous considérons un chemin à la fois, nous n'avons pas à introduire de nouvelle variable pour t. On peut simplement dire que puisque t = y, alors t n'est plus 0.

Nous continuons à descendre et à arriver au point où nous arrivons à une autre branche. Quelle est la nouvelle hypothèse que nous devons faire pour continuer dans cette voie? Il s'agit d'une hypothèse selon laquelle t <y.

Qu'est-ce que t? Si vous recherchez la bonne branche, nous verrons que t = y. Et dans notre tableau, T = y et Y = y. Il en découle logiquement que notre restriction ressemble à y <y, ce qui ne peut pas l'être.



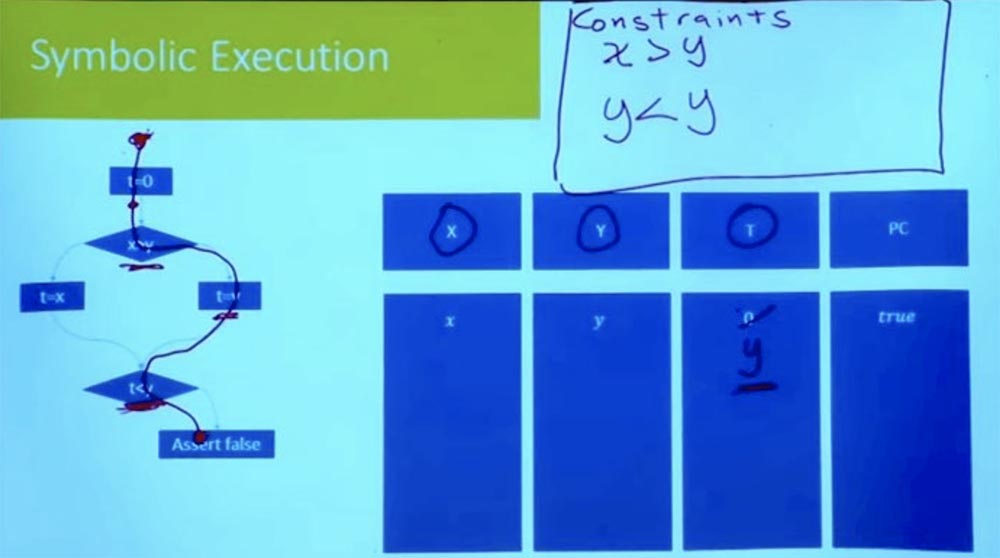
Ainsi, nous avions tout en ordre jusqu'à ce que nous atteignions ce point t <y. Jusqu'à ce que nous arrivions à la déclaration fausse, nous avons toutes les inégalités pour être correctes. Mais cela ne fonctionne pas, car lors de l'exécution des tâches de la bonne branche, nous avons une incohérence logique.

Nous avons ce qu'on appelle souvent la condition du chemin. Cette condition doit être vraie pour que le programme aille dans ce sens. Mais nous savons que cette condition ne peut pas être remplie, il est donc impossible pour le programme de suivre cette voie. Donc, ce chemin a maintenant été complètement éliminé, et nous savons que ce bon chemin ne peut pas être parcouru.

Et dans l'autre sens? Essayons de passer par la branche gauche d'une manière différente. Quelles seront les conditions de ce parcours? Encore une fois, notre état symbolique commence à t = 0, et X et Y sont égaux aux variables x et y.



À quoi ressemble la restriction de chemin dans ce cas maintenant? Nous désignons la branche gauche comme True et la branche droite comme False et considérons en outre la valeur t = x. À la suite du traitement logique des conditions t = x, x> y et t <y, nous obtenons que nous avons simultanément ce que x> y et x <y.



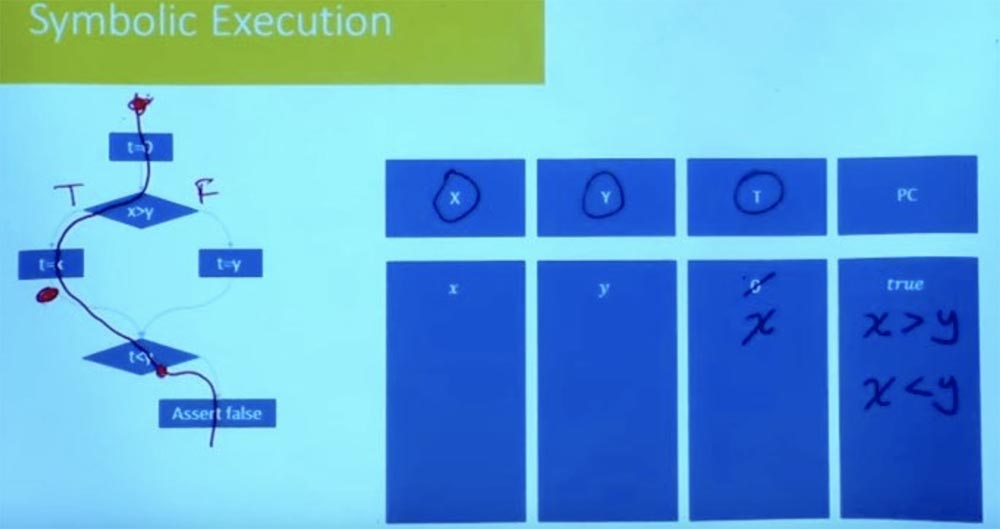
Il est clair que cette condition du chemin n'est pas satisfaisante. Nous ne pouvons pas avoir x qui soit à la fois plus grand et plus petit que y. Il n'y a aucune affectation à une variable X qui satisfait les deux contraintes. Ainsi, cela nous indique que l'autre voie est également insatisfaisante.

Il s'avère qu'à ce moment nous avons exploré toutes les voies possibles dans le programme qui pourraient nous conduire à cet état. Nous pouvons effectivement établir et vérifier qu'il n'y a aucun moyen possible de nous conduire à la déclaration fausse.
Public: Dans cet exemple, vous avez montré que vous aviez étudié l'avancement d'un programme dans toutes les branches possibles. Mais l'un des avantages de l'exécution symbolique est que nous n'avons pas besoin d'étudier tous les chemins exponentiels possibles. Alors, comment éviter cela dans cet exemple?

Professeur: C'est une très bonne question. Dans ce cas, vous faites un compromis entre l'exécution du personnage et la spécificité que vous souhaitez être. Donc, dans ce cas, nous n'utilisons pas tant l'exécution symbolique que la première fois que nous avons examiné le flux du programme sur les deux branches simultanément. Mais grâce à cela, nos limites sont devenues très, très simples.

Les restrictions individuelles «d'une manière après l'autre» sont très simples, mais vous devez le faire encore et encore, en étudiant toutes les branches existantes, et de manière exponentielle - et toutes les manières possibles.
Il existe de manière exponentielle de nombreux chemins, mais pour chaque chemin dans son ensemble, il existe également un ensemble exponentiellement important de données d'entrée qui peuvent suivre ce chemin. Donc, cela vous donne déjà un gros avantage, car au lieu d'essayer toutes les entrées possibles, vous essayez d'essayer de toutes les manières possibles. Mais pouvez-vous faire quelque chose de mieux?

Il s'agit d'un domaine dans lequel de nombreuses expérimentations ont été réalisées concernant l'exécution symbolique, par exemple, l'exécution simultanée de plusieurs chemins. Dans les documents de cours, vous avez rencontré l'heuristique et un ensemble de stratégies que les expérimentateurs ont utilisées pour rendre la recherche plus soluble.

Par exemple, l'une des choses qu'ils font, c'est qu'ils explorent les uns après les autres, mais ne le font pas complètement à l'aveugle. Ils vérifient les conditions du chemin après chaque étape franchie. Supposons qu'ici dans notre programme, au lieu de dire «faux», il y aurait un arbre complexe de programmes, un graphique de flux de contrôle.



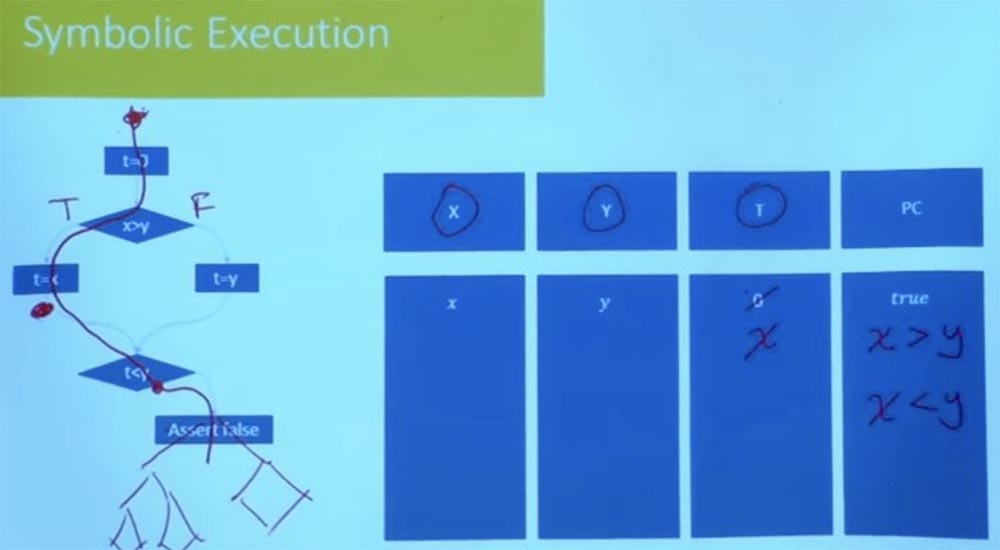
Vous n'avez pas besoin d'attendre jusqu'à la fin pour vérifier que ce chemin est faisable. A ce moment, lorsque vous atteignez la condition t <y, vous savez déjà que ce chemin n'est pas satisfaisant, et vous n'irez jamais dans cette direction. Par conséquent, couper les mauvaises branches au début du programme réduit la quantité de travail empirique. Une exploration raisonnable du chemin empêche la possibilité d'échec du programme à l'avenir. Bon nombre des outils pratiques utilisés aujourd'hui commencent principalement par des tests aléatoires pour obtenir l'ensemble initial de chemins, après quoi ils commenceront à explorer les chemins dans le quartier. Ils traitent de nombreuses options pour l'exécution possible du programme pour chacune des branches, se demandant ce qui se passe sur ces chemins.

C'est particulièrement utile si nous avons un bon ensemble de tests. Vous exécutez votre test et constatez que ce morceau de code n'est pas en cours d'exécution. Par conséquent, vous pouvez prendre le chemin le plus proche de l'implémentation du code et demander si ce chemin peut être modifié pour qu'il aille dans la bonne direction?



Mais au moment où vous essayez de faire tous les chemins en même temps, des restrictions commencent à devenir insolubles. Par conséquent, ce que vous pouvez faire est d'exécuter une fonction à la fois, tandis que vous pouvez apprendre tous les chemins d'une fonction ensemble. Si vous essayez de faire de gros blocs, vous pouvez en général explorer toutes les manières possibles.

La chose la plus importante est que pour chaque branche, vous vérifiez vos restrictions et déterminez si cette branche peut vraiment aller dans les deux sens. Si elle ne peut pas suivre les deux chemins, vous économisez du temps et des efforts en ne suivant pas la direction où elle ne peut pas aller. De plus, je ne me souviens pas des stratégies spécifiques qu'ils utilisent pour trouver des moyens plus susceptibles de produire de très bons résultats. Mais couper les mauvaises branches au stade initial est très important.

Jusqu'à présent, nous parlions principalement de «code jouet», de variables entières, de branches, de choses très simples. Mais que se passe-t-il lorsque vous avez un programme plus complexe? En particulier, que se passe-t-il lorsque vous avez un programme qui comprend un groupe?



Historiquement, le tas de hanches a été la malédiction de toute analyse de logiciel parce que les choses propres et élégantes de l'époque de Fortran explosent complètement lorsque vous essayez de les exécuter à l'aide de programmes C dans lesquels vous allouez de la mémoire à gauche et à droite. Là, vous avez des superpositions et tout le désordre associé au programme avec de la mémoire allouée et des pointeurs arithmétiques. C'est l'un des domaines où l'exécution symbolique a une capacité exceptionnelle à raisonner sur les programmes.

Alors, comment faisons-nous cela? Oublions les branches et contrôlons le flux pendant un moment. Nous avons un programme simple ici. Il alloue de la mémoire, l'annule et obtient un nouveau pointeur y à partir du pointeur x. Puis elle écrit quelque chose dans y et vérifie si la valeur stockée dans le pointeur y est égale à la valeur stockée dans le pointeur x?

Sur la base d'une connaissance de base de C, vous pouvez voir que cette vérification n'est pas effectuée car x est réinitialisé et y = 25, donc x indique un emplacement différent. Jusqu'à présent, tout va bien pour nous.
La façon dont nous modélisons le tas, et la façon dont le tas est modélisé sur la plupart des systèmes, utilise la représentation du tas en C, où il ne s'agit que d'une gigantesque base d'adresses, un gigantesque tableau dans lequel vous pouvez placer vos données.
Cela signifie que nous pouvons représenter notre programme comme un très grand ensemble de données mondiales, qui sera appelé MEM. Il s'agit d'un tableau qui va essentiellement mapper les adresses aux valeurs. Une adresse n'est qu'une valeur de 64 bits. Et que se passera-t-il après avoir lu quelque chose de cette adresse? Cela dépend de la façon dont vous modélisez la mémoire.

Si vous le modélisez au niveau des octets, vous obtenez un octet. Si vous le modélisez au niveau des mots, vous obtenez un mot. Selon le type d'erreurs qui vous intéresse et selon que vous vous souciez de l'allocation de mémoire ou non, vous la modéliserez un peu différemment, mais généralement la mémoire n'est qu'un tableau d'adresse à valeur.



L'adresse n'est donc qu'un entier. D'une certaine manière, peu importe ce que pense C de l'adresse, c'est juste un entier 64 bits ou 32 bits, selon votre machine. Il s'agit simplement d'une valeur indexée dans cette mémoire. Et ce que vous pouvez mettre en mémoire, vous pouvez lire à partir de cette mémoire.

Par conséquent, des choses comme l'arithmétique des pointeurs deviennent simplement des arithmétiques entières. En pratique, il y a quelques difficultés, car en C, l'arithmétique des pointeurs connaît les types de pointeurs, et ils augmenteront proportionnellement à la taille. Donc, en conséquence, nous obtenons la ligne suivante:

y = x + 10;  sizeof (int)



Mais ce qui compte vraiment, c'est ce qui se passe lorsque vous écrivez et lisez de la mémoire. Sur la base du pointeur que 25 doit être écrit en y, je prends un tableau de mémoire et l'indexe avec y. Et j'écris 25 à cet emplacement mémoire.

Ensuite, je passe à l'instruction MEM [y] = MEM [x], je lis la valeur de l'emplacement y en mémoire, je lis la valeur de l'emplacement x en mémoire et je les compare. Je vérifie donc si elles correspondent ou non.

Il s'agit d'une hypothèse très simple, vous permettant de passer d'un programme qui utilise le tas à un programme qui utilise ce gigantesque tableau global représentant la mémoire. Cela signifie que maintenant, lorsque vous parlez de programmes qui gèrent le tas, vous n'avez vraiment plus besoin de parler de programmes qui gèrent le tas. Vous réussirez parfaitement à parler de tableaux, et non de tas.

Voici une autre question simple. Et la fonction malloc? Vous pouvez simplement prendre et utiliser l'implémentation malloc en C, garder une trace de toutes les pages en surbrillance, garder une trace de tout ce qui a été libéré, juste avoir une liste gratuite, et c'est assez. Il s'avère qu'à de nombreuses fins et pour de nombreux types d'erreurs, vous n'avez pas besoin de malloc pour être complexe.

En fait, vous pouvez passer de malloc, qui ressemble à ceci: x = malloc (sizeof (int) * 100), à malloc de ce type:

POS = 1
Int malloc (int n) {
rv = POS
POS + = n;
}

Ce qui dit simplement: "Je vais enregistrer le compteur pour le prochain espace libre en mémoire, et chaque fois que quelqu'un demande une adresse, je lui donne cet emplacement et augmente cette position, puis je renvoie RV." Dans ce cas, ce malloc au sens traditionnel est complètement ignoré.



Dans ce cas, il n'y a pas de libération de mémoire. La fonction continue simplement de se déplacer de plus en plus loin de la mémoire, et de plus en plus loin, et c'est là qu'elle se termine sans aucune libération. Elle ne se soucie pas vraiment non plus du fait qu'il existe des zones de mémoire dans lesquelles cela ne vaut pas la peine d'être écrit, car il existe des adresses spéciales d'une importance particulière réservées au système d'exploitation.

Il ne modélise rien qui complique l'écriture de la fonction malloc, mais seulement à un certain niveau d'abstraction, lorsque vous essayez de parler d'une sorte de code complexe qui effectue des manipulations de pointeur.

En même temps, vous ne vous souciez pas de libérer de la mémoire, mais vous vous demandez si le programme va, par exemple, écrire en dehors d'un tampon, auquel cas cette fonction malloc peut être assez bonne.



Et cela se produit en fait très, très souvent lorsque vous effectuez une exécution symbolique de code réel. Une étape très importante est la modélisation des fonctions de votre bibliothèque. La façon dont vous modélisez les fonctions de bibliothèque aura un impact énorme, d'une part, sur les performances et l'évolutivité de l'analyse, mais d'autre part, cela affectera également la précision.

Donc, si vous avez un tel malloc modèle "jouet", comme celui-ci, il agira très rapidement, mais en même temps il y aura certains types d'erreurs que vous ne pourrez pas remarquer. Ainsi, par exemple, dans ce modèle, j'ignore complètement les distributions, donc je peux obtenir une erreur si quelqu'un a accès à l'espace non alloué. Par conséquent, dans la vraie vie, je n'utiliserai jamais ce modèle de malloc Mickey Mouse.

Il s'agit donc toujours d'un équilibre entre la précision de l'analyse et l'efficacité. Et plus les modèles de fonctions standard sont complexes, comme malloc get, moins leur analyse est évolutive. Mais pour certaines classes d'erreur, vous aurez besoin de ces modèles simples. Par conséquent, diverses bibliothèques en C sont d'une grande importance, qui sont nécessaires pour comprendre ce qu'un tel programme fait réellement.

Par conséquent, nous avons réduit le problème du raisonnement sur le tas en raisonnant sur le programme avec des tableaux, mais je ne vous ai pas vraiment expliqué comment parler du programme avec des tableaux. Il s'avère que la plupart des solveurs SMT prennent en charge la théorie des matrices.



L'idée est que si a est un tableau, il existe une notation qui vous permet de prendre ce tableau et de créer un nouveau tableau, où l'emplacement i est mis à jour à la valeur e. Est-ce clair?

Par conséquent, si j'ai un tableau a, et je fais cette opération de mise à jour, puis j'essaie de lire la valeur de k, cela signifie que la valeur de k sera égale à la valeur de k dans le tableau a, si k est différent de i, et il sera égal à e, si k est égal à i.

La mise à jour d'un tableau signifie que vous devez prendre l'ancien tableau et le mettre à jour avec un nouveau tableau. Eh bien, si vous avez une formule qui inclut la théorie des tableaux, c'est pourquoi j'ai commencé avec un tableau zéro, qui est partout représenté simplement par des zéros.



Ensuite, j'écris 5 à l'emplacement i et 7 à l'emplacement j, après quoi je lis à partir de k et vérifie si c'est 5 ou non. Ensuite, il peut être développé en utilisant la définition de quelque chose qui dit, par exemple: «si k est i et k est y, alors que k est différent de j, alors oui, ce sera 5, sinon ce ne sera pas 5 ".

Et dans la pratique, les solveurs SMT ne se contentent pas d'étendre cela à de nombreuses formules booléennes, ils utilisent cette stratégie de va-et-vient entre le solveur SAT et le moteur, qui est capable de parler de la théorie des matrices pour effectuer ce travail.

L'important est qu'en s'appuyant sur cette théorie des tableaux, en utilisant la même stratégie que nous avons appliquée pour générer des formules d'entiers, vous pouvez réellement générer des formules qui incluent la logique du tableau, les mises à jour du tableau, les axes du tableau, l'itération du tableau. Et tant que vous corrigez votre chemin, ces formules sont très faciles à générer.
Si vous ne corrigez pas vos chemins, mais que vous souhaitez créer une formule qui correspond au passage du programme sur tous les chemins, cela est également relativement facile. La seule chose à laquelle vous devez faire face est un type spécial de boucles.

Les dictionnaires et les cartes sont également très faciles à modéliser à l'aide de fonctions non définies. En fait, la théorie des tableaux elle-même n'est qu'un cas particulier d'une fonction indéfinie. Avec l'aide de telles fonctions, des choses plus compliquées peuvent être faites. Dans le solveur SMT moderne, il existe une prise en charge intégrée pour le raisonnement sur les ensembles et les opérations sur les ensembles, ce qui peut être très utile si vous parlez d'un programme qui comprend le calcul d'ensembles.

Lors de la conception d'un de ces outils, la phase de modélisation est très importante. Et le point n'est pas seulement la façon dont vous modélisez des fonctions de programme complexes selon vos théories, par exemple, des choses comme la réduction de tas en tableaux. Le point est également les théories et les solveurs que vous utilisez. Il existe un grand nombre de théories et de solveurs ayant des relations différentes, pour lesquels il est nécessaire de choisir un compromis raisonnable entre efficacité et coût.



La plupart des outils pratiques adhèrent à la théorie des vecteurs de bits et, si nécessaire, peuvent utiliser la théorie des tableaux pour modéliser des tas. En général, les outils pratiques tentent d'éviter les théories plus complexes, telles que la théorie des ensembles. C'est parce qu'ils sont généralement moins évolutifs dans certains cas, si vous n'avez pas affaire à un programme qui nécessite vraiment ce type d'outil pour fonctionner.

Public: en plus de l'étude des performances symboliques, sur quoi les développeurs se concentrent-ils?

: — , . , , , , . , .

, , . , , , , , , , .

, — , , . , , — , JavaScript Python, . , .



, Python. , , : «, , , ». .

, , , , , .
, , , - , , .

, , , . , , Microsoft Word, , , .

, , , , .

, . , , - , - . , , . , .


La version complète du cours est disponible ici .

, . ? ? , 30% entry-level , : VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps $20 ? ( RAID1 RAID10, 24 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 cœurs) 10 Go DDR4 240 Go SSD 1 Gbit / s jusqu'en décembre gratuitement en payant pour une période de six mois, vous pouvez commander ici .

Dell R730xd 2 ? 2 Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 $249 ! . c Dell R730xd 5-2650 v4 9000 ?