Cours MIT "Sécurité des systèmes informatiques". Conférence 10: Exécution symbolique, partie 2

Institut de technologie du Massachusetts. Cours magistral # 6.858. "Sécurité des systèmes informatiques." Nikolai Zeldovich, James Mickens. 2014 année

Computer Systems Security est un cours sur le développement et la mise en œuvre de systèmes informatiques sécurisés. Les conférences couvrent les modèles de menace, les attaques qui compromettent la sécurité et les techniques de sécurité basées sur des travaux scientifiques récents. Les sujets incluent la sécurité du système d'exploitation (OS), les fonctionnalités, la gestion du flux d'informations, la sécurité des langues, les protocoles réseau, la sécurité matérielle et la sécurité des applications Web.

Cours 1: «Introduction: modèles de menace» Partie 1 / Partie 2 / Partie 3
Conférence 2: «Contrôle des attaques de pirates» Partie 1 / Partie 2 / Partie 3
Conférence 3: «Débordements de tampon: exploits et protection» Partie 1 / Partie 2 / Partie 3
Conférence 4: «Séparation des privilèges» Partie 1 / Partie 2 / Partie 3
Conférence 5: «D'où viennent les systèmes de sécurité?» Partie 1 / Partie 2
Conférence 6: «Opportunités» Partie 1 / Partie 2 / Partie 3
Conférence 7: «Native Client Sandbox» Partie 1 / Partie 2 / Partie 3
Conférence 8: «Modèle de sécurité réseau» Partie 1 / Partie 2 / Partie 3
Conférence 9: «Sécurité des applications Web», partie 1 / partie 2 / partie 3
Conférence 10: «Exécution symbolique» Partie 1 / Partie 2 / Partie 3

Public: Il semble que vous n'ayez pas parlé de la façon dont les bits sont utilisés pour stocker un entier entier.

Professeur: C'est une très bonne question. Et cela a vraiment à voir avec la façon dont vous définissez vos limites, non? Par conséquent, si vous regardez notre exemple simple dès le début, vous verrez que nous avons supposé la présence d'entiers que nous avons étudiés à l'école primaire. Dans le même temps, nous avons complètement décidé d'ignorer les erreurs de débordement. Si vous vous souciez des erreurs de débordement et qu'il est important pour vous qu'il n'y ait pas de telles erreurs, l'utilisation de nombres mathématiquement entiers n'aidera pas à résoudre le problème.



Ce dont vous avez besoin, c'est de présenter ces quantités non pas comme des entiers, mais comme des vecteurs de bits. Lorsque vous les représentez comme des vecteurs de bits, vous devez utiliser une vue plus large des choses. Nous revenons ici aux solveurs SMT. Un aspect de la théorie modulaire est que le solveur lui-même est extensible en utilisant différentes théories.

Les théories les plus populaires sont les théories vectorielles à bits de longueur fixe. Cela signifie que si vous interprétez vos formules dans la théorie des vecteurs de bits de longueur fixe, vous devez d'abord définir la longueur des vecteurs de bits. Autrement dit, vous devez indiquer explicitement que cela sera utilisé pour les vecteurs de bits de 32 bits de long, ou 8 bits, ou 64 bits.



Il existe une autre théorie appelée théorie des tableaux TOA. Et nous en parlerons un peu plus. Contrairement à la théorie des vecteurs de bits, qui est conçue pour des objets de longueur fixe, la théorie des tableaux est destinée aux collections dont la taille est a priori inconnue.

Or, dans la pratique, personne n'utilise la théorie des tableaux, par exemple, pour modéliser des entiers, car elle est trop chère. Parler d'un problème coûte beaucoup plus cher si vous ne connaissez pas ses limites. Par conséquent, en règle générale, les gens utilisent la théorie d'une longueur fixe de vecteurs de bits dans les discussions d'entiers ou même de symboles.

Une autre théorie très répandue est la théorie de l'arithmétique des entiers réels, et en particulier l'arithmétique des entiers linéaires.



Les gens aiment vraiment cette théorie parce qu'elle fournit un raisonnement efficace, mais ce n'est pas trop bon quand vous parlez de programmes, car ici vous vous souciez vraiment des problèmes de débordement. Mais cette théorie est largement utilisée pour de nombreuses choses.

Une autre théorie qui est souvent utilisée est la théorie des fonctions non interprétées. Que signifie cette théorie?



Cela signifie que vous avez une certaine formule. Dans cette formule, vous savez que vous appelez une fonction, mais vous ne savez rien sur cette fonction, sauf que si vous y insérez une entrée, vous obtiendrez la même sortie.

Il s'avère que cela est très utile pour raisonner sur des choses comme l'utilisation de code à virgule flottante, la modélisation, les sinus, les cosinus, les racines carrées. Des discussions détaillées sur de telles choses peuvent prendre beaucoup de temps et coûter cher. Mais utiliser cette théorie vous permet de dire: «Écoutez, je me fiche de ce que fait la fonction sinus. Je me fiche de ce qu’elle donnera exactement. J'ai juste besoin de savoir que si j'appelle la fonction sinus à divers endroits du programme avec une entrée spécifique, j'obtiendrai des données du même type à la sortie. C'est assez pour moi de raisonner sur mon programme. »

Et par conséquent, les opérations les plus courantes dans l'analyse de systèmes réels sont des vecteurs de bits qui fonctionnent avec des entiers, des journaux et des pointeurs. En fait, les pointeurs sont souvent représentés par un entier, car parfois vous ne définissez pas de vecteurs de bits sur les pointeurs. Mais parfois, vous devez le faire, puis vous ne pouvez plus utiliser d'entiers.

Nous avons donc examiné ce qu'un solveur SMT peut faire pour vous. Comment ça marche vraiment? Qu'est-ce qui les fait fonctionner?

En fait, les solveurs SMT s'appuient sur notre capacité à résoudre les problèmes de faisabilité des formules booléennes SAT, sur la capacité à considérer les problèmes associés uniquement aux contraintes purement booléennes et aux variables booléennes, et à nous dire si vous vous assurerez que le programme affecte ou non les valeurs affectées à ces variables booléennes. .

C'est quelque chose que pendant de très nombreuses années a enseigné aux étudiants seniors, disant que c'est en fait une tâche NP-complète, et dans les cas où quelque chose se résume à SAT, vous ne devriez pas le faire. Mais il s'avère que nous avons en fait de très bons solveurs SAT.

Donc, je vais vous dire l'idée de base du fonctionnement des solveurs SAT. Cela réside dans le fait que vous prenez toutes vos restrictions sur les variables booléennes et les placez dans la base de données. Vous ne pourrez peut-être pas voir clairement les petites lettres à l'écran, mais c'est tout ce que je peux faire.



Je commenterai et en parlerai au cours de l'action, et plus tard je publierai les diapositives afin que vous puissiez voir ce qui y est écrit.

Donc, ici, dans la tâche SAT, nous avons toutes ces variables représentant des inconnues booléennes, non? Nous voulons savoir s'il est possible pour X d'être vrai en même temps (X = VRAI), et Y pour être vrai et Z pour être vrai. Ce sont nos inconnues. De plus, toutes les restrictions sont sous forme conjonctive normale. Cela signifie que toutes nos restrictions sont sous la forme de X1 = true, ou X2 = true, ou X3 = true.



Sous cette forme, nous avons toutes nos limitations, qui disent que X1 est vrai, ou X2 est faux, ou X3 est faux. Vous vous souvenez probablement des mathématiques discrètes que toute formule booléenne peut être représentée sous une forme connective normale. Cela signifie que toute représentation que vous utilisez pour représenter des formules booléennes, vous pouvez très facilement les convertir dans ce format.

Nous avons donc une base de données avec de nombreuses limitations de ce formulaire. Le solveur SAT choisira une de ces variables de manière aléatoire, supposons qu'il s'agit de X1. Et il dira: «pourquoi ne pas mettre X1 à vrai? Je ne sais rien de ces restrictions, je peux donc supposer qu’il en est bien ainsi. " Et puis il arrive que vous ayez des restrictions qui, par exemple, indiquent que X1 est faux ou X7 est vrai.

Donc, si vous savez que X1 est vrai et que vous savez que X1 est faux ou X7 est vrai, que savez-vous de X7?

Public: ça doit être vrai!

Professeur: oui, ça doit être vrai. Sinon, cette restriction ne sera pas respectée. Donc, maintenant vous avez distribué cette valeur de X1 à X7. Supposons que vous sélectionnez maintenant une autre variable aléatoire, telle que X5.



Supposons maintenant que vous ayez une restriction qui dit: soit X7 est faux, soit X6 est vrai, soit X5 est faux. Donc, j'ai X5 = vrai et X7 = vrai. Cela signifie que X6 devrait désormais également être vrai. Sinon, cette restriction serait violée. Ainsi, le système conclut que X6 doit être vrai et continue le processus, effectuant les vérifications disponibles et examinant toutes les offres disponibles. Le système vérifie s'il y a d'autres choses qui sont impliquées par les contrôles qu'il a. Et elle suit ces significations jusqu'à ce qu'une des deux choses se produise.

La première est que vous continuez à suivre les conséquences et essayez des choses aléatoires, et finalement vous définissez la valeur pour chaque variable sans jamais rencontrer de contradiction. Vous avez donc tout fait correctement.

La seconde - vous êtes confronté à une contradiction, puis vous revenez à la condition qui a rendu X4 vrai, à l'exclusion de la condition qui a fait que X4 soit faux. Mais il y a une règle d'algèbre booléenne que tout le monde devrait connaître: une variable ne peut pas être à la fois vraie et fausse en même temps.



Et cela dit que vous êtes confronté à une contradiction, vous avez évidemment fait quelque chose de mal dans l'une de ces tâches aléatoires que vous avez essayé de terminer.

Analysons cette contradiction et voyons quel type de tâches a conduit à cette contradiction. Sur la base des missions qui ont conduit à cette contradiction, inventons une nouvelle clause de conflit qui résume cette contradiction.

Que se passe-t-il si X1 est faux, et X5 est faux, et X9 est également faux? Essentiellement, cela est basé sur ce que j'ai appris de ces affectations aléatoires, au cours desquelles j'ai découvert qu'une de ces choses doit être vraie, qu'il ne peut pas être que X1 est vrai et X5 est vrai, et X9 était faux, cela ne peut pas être.

Je sais que cela ne peut pas arriver, car quand j'ai essayé de le faire, tout a «explosé», j'ai terminé le programme avec une contradiction.

Et donc, le solveur SAT essaie de terminer des tâches aléatoires, vérifiant comment elles se déroulent. Lorsqu'il rencontre des contradictions, il analyse l'ensemble des conséquences qui ont conduit à ces contradictions et forme finalement une nouvelle restriction, qui garantit que le solveur ne rencontre plus jamais cette contradiction particulière, ce problème particulier.
Ainsi, nous pouvons imaginer le solveur SAT comme une «boîte noire» qui donne une contrainte booléenne et peut dire si elle est satisfaisante ou non. Les solveurs SMT sont construits sur les meilleurs solveurs SAT. Ils peuvent utiliser la puissance des solveurs SAT pour résoudre des problèmes NP-complets avec un raisonnement orienté sujet sur les théories prises en charge.

Pour avoir une idée de comment cela fonctionne, supposons que vous ayez une telle formule.



Est-ce faisable? Pouvons-nous lui trouver un test satisfaisant? Le solveur SMT peut séparer une partie de cette formule, ce qui nécessite un raisonnement en théorie des nombres entiers. Nous utilisons des structures booléennes pour séparer les formules. Nous avons donc les formules F1, F2, F3 et F4.



Maintenant, c'est une tâche booléenne purement logique - puis-je trouver une tâche satisfaisante pour cela? Le solveur SAT peut dire: «oui, je peux trouver quelque chose qui satisfait cette tâche en faisant F1 = true, F2 = true et F3 = true». Cela satisfait la spécification de la formule booléenne.

\

Donc, maintenant nous avons une question que nous pouvons poser au solveur pour une zone spécifique, dans ce cas, c'est juste un solveur arithmétique linéaire. Nous pouvons donc aller au solveur linéaire Theory Solver et dire: «Le solveur SAT déclare que c'est une affectation raisonnable, et que si je peux faire fonctionner cette affectation, ma formule sera satisfaite.»

Je peux dire que F1 est X> 5, F2 est Y <5 et F3 est Y> X. Je peux donc demander au solveur SAT s'il est possible d'obtenir de tels X et Y pour que X soit> 5, Y est < 5, et dans ce cas, Y serait> X? Maintenant, c'est une question d'arithmétique purement linéaire, il n'y a pas de logique booléenne.

Et quelle est la réponse à cette question? Non. Il est impossible de satisfaire simultanément à ces conditions.
Il existe donc des méthodes traditionnelles pour résoudre des problèmes linéaires. Vous pouvez utiliser la méthode simplex, par exemple, pour résoudre des systèmes d'inégalités linéaires. Il existe de nombreuses méthodes qui peuvent être utilisées pour résoudre des systèmes d'inégalités linéaires.



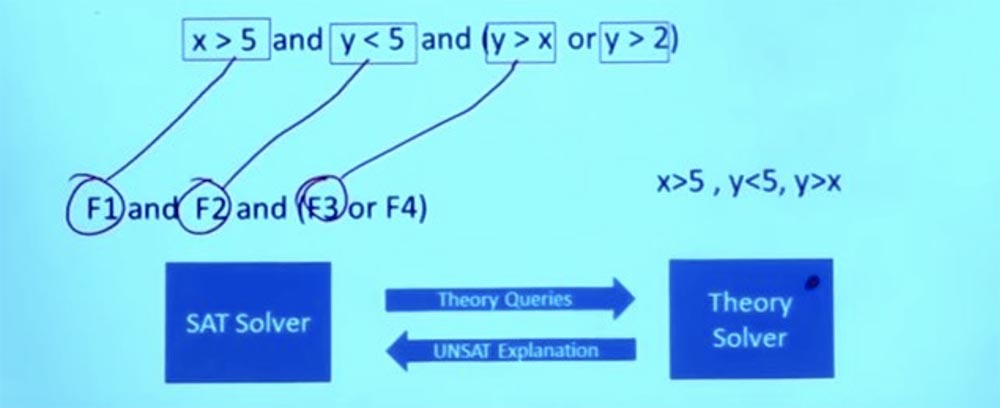
Ainsi, le solveur SAT envoie des questions théoriques au solveur de théorie. L'essentiel est que les solveurs du solveur de théorie connaissent tout de ces problèmes et peuvent donner une réponse précise à la question de savoir si ces conditions fonctionneront.

Dans ce cas, le solveur théorique traite la demande, découvre que cette affectation de conditions ne peut pas fonctionner, revient au solveur SAT et dit: «ces choses que vous avez faites ne fonctionneront pas»!

Mais il ne se contente pas de dire oui ou non, mais explique pourquoi quelque chose ne fonctionnera pas. Du fait que ces formules ne fonctionnent pas, le solveur de théorie conclut que F1 et F2 et F3 ne peuvent pas exister simultanément, et indique au solveur SAT que ces 3 formules sont mutuellement exclusives.

Alors maintenant, nous avons quelques informations que je peux retourner au solveur SAT et lui demander: «Hé, vous pouvez me donner une solution qui satisfait non seulement la contrainte que nous avions au début, mais aussi la nouvelle contrainte que Theory a découverte solveur "?

Y a-t-il un autre objectif qui satisfait maintenant à ces deux limitations?



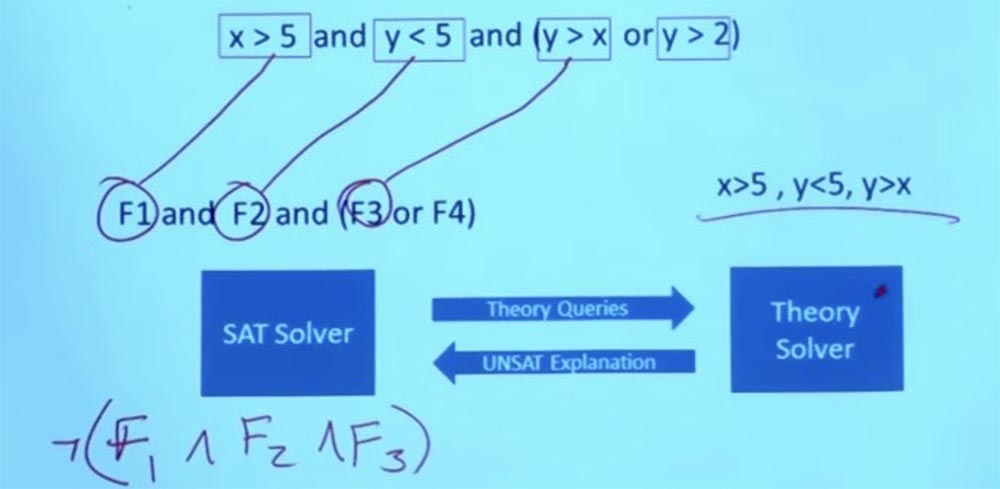
Donc, nous rejetons la restriction initiale X> 5, Y <5, Y> X, cela ne nous dérange plus.



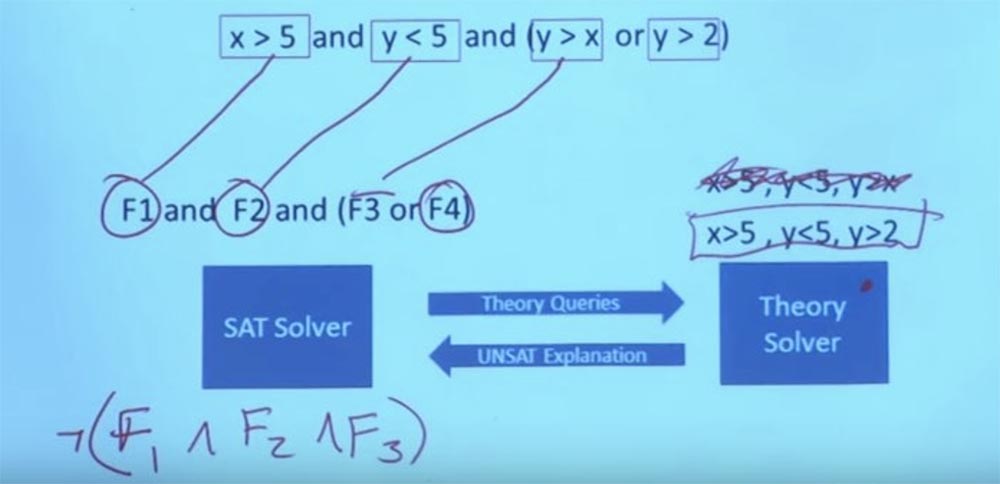
Nous avons une nouvelle restriction que nous pouvons définir pour notre solveur de théorie - X> 5, Y <5, Y> 2. Nous pouvons faire Y égal à 3 et X égal à 6, puis cela fonctionnera. Vous avez maintenant une tâche qui satisfait la formule en théorie et satisfait la structure booléenne de cet objectif. Et avec cela, le système peut revenir et dire: "oui, c'est la tâche qui satisfait toutes vos limites." Il s'agit de l'interaction entre le solveur de théorie et le solveur SAT. En réalité, cela signifie pouvoir parler de formules booléennes très, très grandes et très complexes. Voici ce qui rend possible l'exécution symbolique.

Nous allons maintenant examiner la question suivante - comment s'effectue la transition du programme aux restrictions que nous pouvons fournir au solveur SMT.

Public: La construction d'un solveur SMT est-elle complète ou non?

Professeur: Le solveur SMT est essentiellement un problème canonique NP-complet. Mais la plupart des résolveurs de nos jours incluent le support de certaines théories qui sont complètement insolubles.

Public: comment abordez-vous ce problème dans votre système?

Professeur: eh bien, à la fin, vous obtiendrez une restriction créée à partir de ce programme. Vous allez le donner au solveur SMT. Et le fait que ce soient des tâches NP-complètes ou qu'elles ne soient pas satisfaisantes signifie que si vous êtes chanceux, vous recevrez une réponse en quelques secondes. Mais si vous n'avez pas de chance, cela peut prendre plus de temps que la création de l'univers.



Public: arrive-t-il que les tâches du système linéaire ne passent pas le SAT?

Professeur: oui, cela arrive vraiment. Cependant, les outils d'ingénierie existants la rendent moins courante. Nous ne résolvons pas les problèmes aléatoires de SAT, nous ne résolvons pas les problèmes complètement aléatoires des vecteurs de bits.

Nous résolvons des problèmes qui ont une certaine structure afin qu'une personne puisse le regarder et avoir une certaine confiance que cela fonctionnera. Nous essayons de créer des arguments dans sa tête pour comprendre pourquoi cela a fonctionné. Et les solveurs SAT utilisent cette structure. Votre problème peut avoir un million de variables booléennes, mais en réalité la plupart de ces variables dépendent beaucoup des valeurs des autres. Ainsi, le nombre de degrés de liberté dans le problème est en réalité bien inférieur à ce que suggèrent des millions de variables.

Public: vous dites que ce n'est pas une question d'examen, mais la vraie vie. Une fois que quelqu'un a construit ce système, il devrait fonctionner et avoir un sens. Donc, cela ne sera probablement pas l'un des discours théoriques inutiles.

Professeur: c'est ça. Par conséquent, dans la pratique, lorsque vous utilisez cet outil, vous définissez toujours des délais d'expiration. En général, tout se passe parce que l'exponentialité ne signifie pas que vous ne pouvez pas le faire. L'exponentialité, c'est-à-dire lorsqu'une fonction est limitée par une autre fonction, signifie simplement qu'il y a un mur de briques devant lequel ces choses fonctionneront, et elles fonctionneront vraiment très rapidement. L'exponentialité fonctionne dans les deux sens.



Lorsque vous vous éloignez de ce mur, les choses se développent très rapidement, mais lorsque vous abordez des problèmes plus petits ou plus simples, ces problèmes s'accélèrent également très, très rapidement. Cela signifie que de nombreux problèmes se terminent très rapidement. Et puis le délai d'expiration du problème se produit. Le but est de concevoir les choses de telle sorte que parmi les problèmes qui se terminent rapidement figurent ceux qui apportent des avantages pratiques. Ce sont des problèmes qui vous indiquent les vulnérabilités de sécurité de votre système, des erreurs, des chemins que vous n'avez peut-être pas explorés auparavant ou des entrées qui violeront vos chemins si vous ne les avez pas étudiés à l'avance.

Donc, nous savons comment passer d'une formule, d'un ensemble de restrictions à une réponse qui dit: «oui, cette formule a une solution, et la voici, c'est une solution». Ou il dira: "cette formule n'est pas satisfaisante, car il n'y a pas d'entrée qui satisfasse vos tâches." Alors, comment pouvons-nous obtenir la formule du programme?

Lorsque vous effectuez une exécution symbolique, vous allez à la branche et vous ne savez pas dans quelle direction elle ira. Il y a deux options pour savoir quoi faire dans ce cas. — , , , .

, , . , SMT-. . , .

: « , , , , ».

, , . . , .

, . , , . , – , . ? , .



, , t=0 false.



, , ? : , , .

, , , , , , .

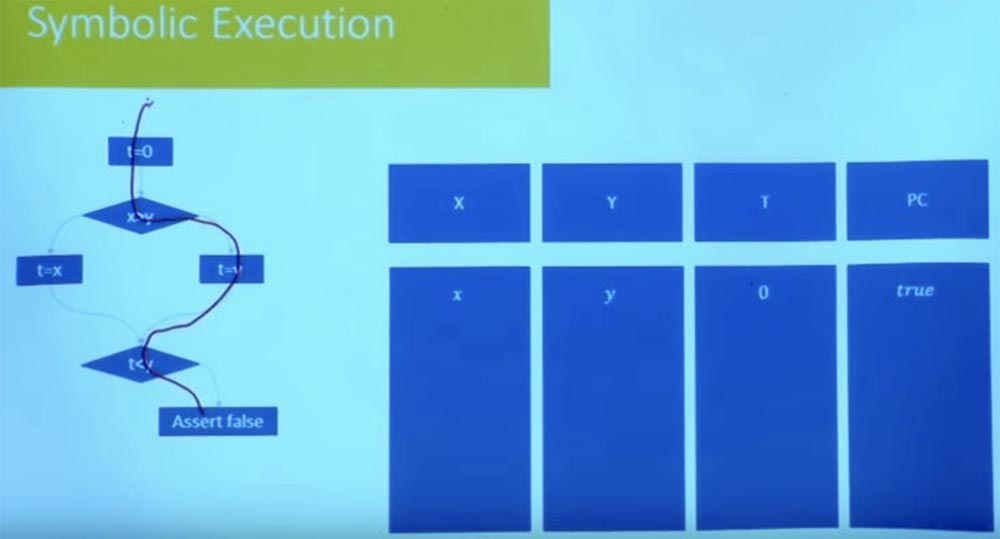
, , t = 0, x, y 0. , . , , X , Y.

, X > Y.



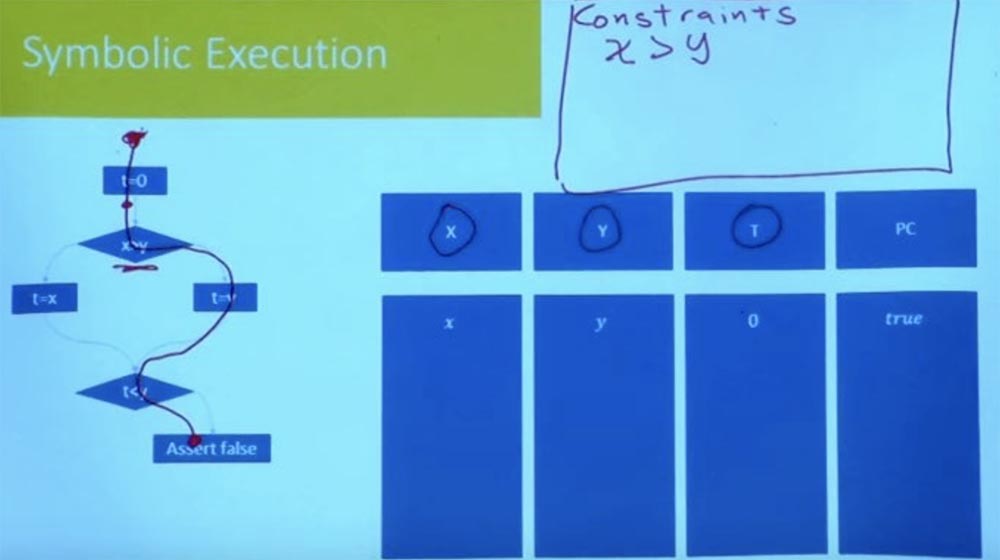
55:00

MIT « ». 10: « », 3


La version complète du cours est disponible ici .

, . ? ? , 30% entry-level , : VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps $20 ? ( RAID1 RAID10, 24 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 cœurs) 10 Go DDR4 240 Go SSD 1 Gbit / s jusqu'en décembre gratuitement en payant pour une période de six mois, vous pouvez commander ici .

Dell R730xd 2 fois moins cher? Nous avons seulement 2 x Intel Dodeca-Core Xeon E5-2650v4 128 Go DDR4 6x480 Go SSD 1 Gbps 100 TV à partir de 249 $ aux Pays-Bas et aux États-Unis! Pour en savoir plus sur la création d'un bâtiment d'infrastructure. classe c utilisant des serveurs Dell R730xd E5-2650 v4 coûtant 9 000 euros pour un sou?