Identifiez la fraude à l'aide de l'ensemble de données Enron. Partie 2, trouver le meilleur modèle

Je vous présente la deuxième partie de l'article sur la recherche de fraude présumée basée sur les données d'Enron Dataset. Si vous n'avez pas lu la première partie, vous pouvez vous familiariser ici .

Nous allons maintenant parler du processus de construction, d'optimisation et de choix d'un modèle qui donnera la réponse: cela vaut-il la peine de soupçonner une personne de fraude?

Plus tôt, nous avons analysé l'un des ensembles de données ouverts qui fournit des informations sur les suspects dans l'affaire Enron et sur la fraude. De plus, le biais dans les données initiales a été corrigé, les lacunes (NaN) ont été comblées, après quoi les données ont été normalisées et la sélection des attributs a été terminée.

Le résultat était familier à beaucoup:

• X_train et y_train - l'échantillon utilisé pour la formation (111 enregistrements);
• X_test et y_test - un échantillon sur lequel la justesse des prédictions de nos modèles sera vérifiée (28 entrées).

En parlant de modèles ... Afin de prédire correctement s'il vaut la peine de suspecter une personne, sur la base de certains signes caractérisant ses activités, nous utiliserons la classification. Les principaux types de modèles utilisés pour résoudre les problèmes dans ce segment peuvent être empruntés à Sklearn:

• Naive Bayes (classificateur naïf Bayes);
• SVM (machine à vecteur de référence);
• K-voisins les plus proches (méthode pour trouver les voisins les plus proches);
• Forêt aléatoire (forêt aléatoire);
• Réseau de neurones.

Il y a aussi une image qui illustre assez bien leur applicabilité:

Parmi eux, il y a un arbre de décision (arbre de décision), familier à beaucoup, mais, peut-être, cela n'a aucun sens dans une tâche d'utiliser cette méthode avec Random Forest, qui est un ensemble d'arbres de décision. Par conséquent, remplacez-le par une régression logistique, qui peut agir comme un classificateur et produire l'une des options attendues (0 ou 1).

Commencer

Nous initialisons tous les classificateurs mentionnés avec des valeurs par défaut:

from sklearn.naive_bayes import GaussianNB from sklearn.linear_model import LogisticRegression from sklearn.neighbors import KNeighborsClassifier from sklearn.svm import SVC from sklearn.neural_network import MLPClassifier from sklearn.ensemble import RandomForestClassifier random_state = 42 gnb = GaussianNB() svc = SVC() knn = KNeighborsClassifier() log = LogisticRegression(random_state=random_state) rfc = RandomForestClassifier(random_state=random_state) mlp = MLPClassifier(random_state=random_state) 

Nous allons également les regrouper afin qu'il soit plus pratique de travailler avec eux comme un agrégat, plutôt que d'écrire du code pour chaque individu. Par exemple, nous pouvons tous les former en même temps:

 classifiers = [gnb, svc, knn, log, rfc, mlp] for clf in classifiers: clf.fit(X_train, y_train) 

Après la formation des modèles, il était temps pour le premier test de leur qualité de prédiction. De plus, nous visualisons nos résultats en utilisant Seaborn:

 from sklearn.metrics import accuracy_score def calculate_accuracy(X, y): result = pd.DataFrame(columns=['classifier', 'accuracy']) for clf in classifiers: predicted = clf.predict(X_test) accuracy = round(100.0 * accuracy_score(y_test, predicted), 2) classifier = clf.__class__.__name__ classifier = classifier.replace('Classifier', '') result = result.append({'classifier': classifier, 'accuracy': accuracy}, ignore_index=True) print('Accuracy is {accuracy}% for {classifier_name}'.format(accuracy=accuracy, classifier_name=classifier)) result = result.sort_values(['classifier'], ascending=True) plt.subplots(figsize=(10, 7)) sns.barplot(x="classifier", y='accuracy', palette=cmap, data=result) 

Jetons un coup d'œil à l'idée générale de la précision des classificateurs:

 calculate_accuracy(X_train, y_train) 

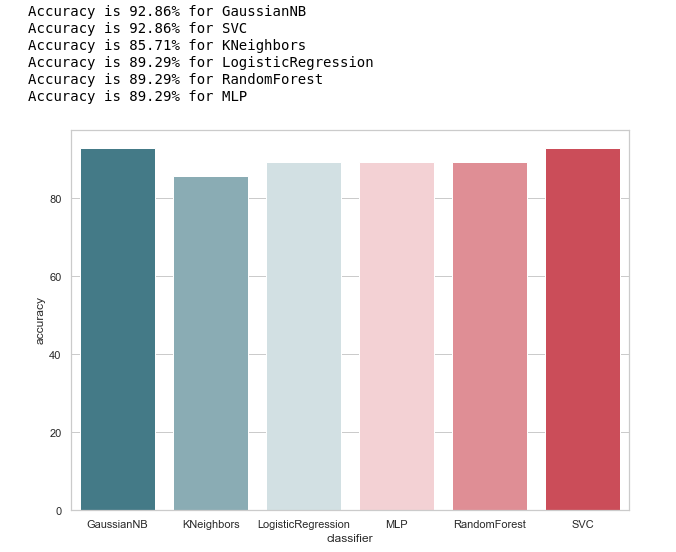
À première vue, il semble assez bon, la précision des prédictions sur l'échantillon test oscille autour de 90%. Il semble que la tâche soit brillante!

 def QuaziAlgo(features): return 0 

Mais encore, avant de nous flatter, construisons une matrice de confusion pour les résultats de prédiction:

 from sklearn.metrics import confusion_matrix def make_confussion_matrices(X, y): matrices = {} result = pd.DataFrame(columns=['classifier', 'recall']) for clf in classifiers: classifier = clf.__class__.__name__ classifier = classifier.replace('Classifier', '') predicted = clf.predict(X_test) print(f'{predicted}-{classifier}') matrix = confusion_matrix(y_test,predicted,labels=[1,0]) matrices[classifier] = matrix.T return matrices 

Nous calculons les matrices d'erreur pour chaque classificateur et, avec cela, voyons ce qu'ils ont prédit:

 matrices = make_confussion_matrices(X_train,y_train) 

Même une représentation textuelle du résultat du travail des classificateurs suffit pour comprendre que quelque chose s'est clairement mal passé.

La méthode des voisins les plus proches n'a révélé aucun suspect dans l'échantillon. Deux questions se posent:

1. Quelle est la raison de ce comportement du classificateur KNeighbors?
2. Pourquoi avons-nous construit des matrices d'erreur si nous ne les utilisons pas, mais regardons simplement les résultats de la prédiction?

Jetez un œil plus profond

Commençons par la deuxième question. Essayons de visualiser nos matrices d'erreur et de présenter les données sous forme graphique pour comprendre où l'erreur de classification se produit:

 import itertools from collections import Iterable def draw_confussion_matrices(row,col,matrices,figsize = (16,12)): fig, (axes) = plt.subplots(row,col, sharex='col', sharey='row',figsize=figsize ) if any(isinstance(i, Iterable) for i in axes): axes = list(itertools.chain.from_iterable(axes)) idx = 0 for name,matrix in matrices.items(): df_cm = pd.DataFrame( matrix, index=['True','False'], columns=['True','False'], ) ax = axes[idx] fig.subplots_adjust(wspace=0.1) sns.heatmap(df_cm, annot=True,cmap=cmap,cbar=False ,fmt="d",ax=ax,linewidths=1) ax.set_title(name) idx += 1 

Nous les affichons sur 2 lignes et 3 colonnes:

 draw_confussion_matrices(2,3,matrices) 

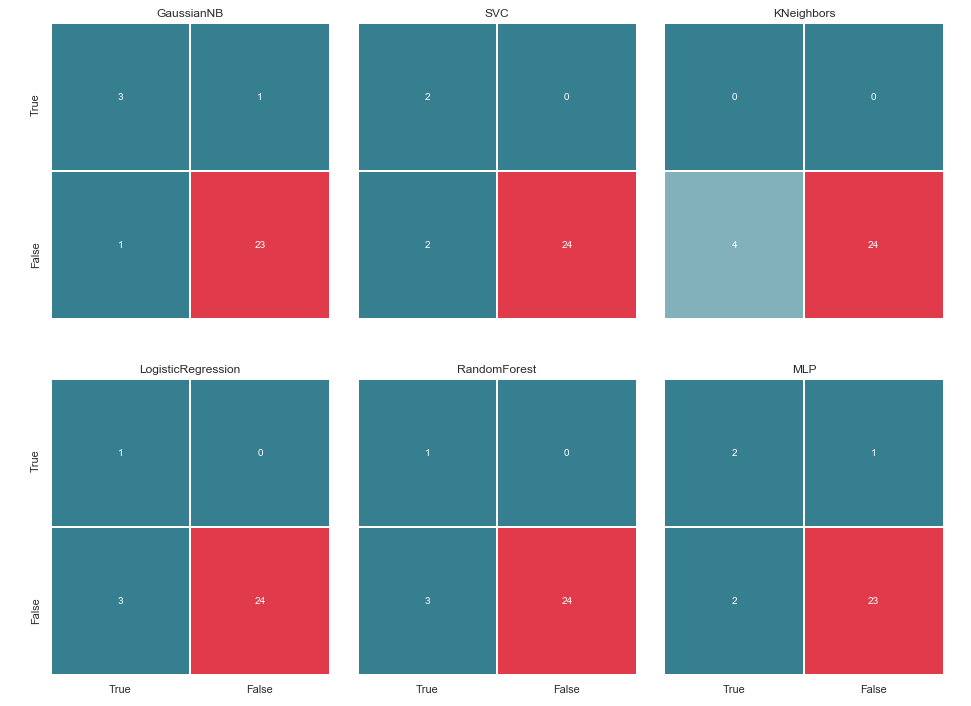
Avant de continuer, il convient de donner quelques éclaircissements. La désignation Vrai, qui se trouve à gauche de la matrice d'erreur d'un classificateur particulier, signifie que le classificateur considérait la personne comme suspecte, la valeur Faux signifie que la personne est au-delà de tout soupçon. De même, Vrai et Faux au bas de l'image nous donne une situation réelle, qui peut ne pas coïncider avec la décision du classificateur.

Par exemple, nous voyons que les décisions des voisins KN avec une précision de prédiction de 85,71% coïncidaient avec la situation réelle lorsque 24 personnes, qui n'étaient pas soupçonnées, étaient incluses dans une liste similaire par le classificateur. Mais 4 personnes de la liste des suspects figuraient également sur cette liste. Si ce classificateur prenait des décisions, peut-être que quelqu'un aurait pu éviter le tribunal.

Ainsi, les matrices d'erreur sont un très bon outil pour comprendre ce qui a mal tourné avec les problèmes de classification. Leur principal avantage est la visibilité, c'est pourquoi nous faisons appel à eux.

Mesures

En termes généraux, cela peut être illustré par l'image suivante:

Et qu'est-ce que TP, TN, FP et une sorte de FN dans ce cas?

$$$TP \ - \ true-positive \ solution \\ TN \ - \ true-negative \ solution \\ FP \ - \ false-positive \ solution \\ FN \ - \ false-negative \ solution$

En d'autres termes, nous nous efforçons de faire coïncider les réponses du classificateur et la situation réelle. C'est-à-dire, pour garantir que tous les nombres sont répartis entre les cellules TP et TN (vraies solutions) et ne tombent pas dans FN et FP (fausses solutions).

Et puisque nous parlons d'abréviations, il est temps de rappeler les métriques de précision (précision) et d'exhaustivité (rappel).

Si vous vous écartez du dossier officiel, la précision peut être exprimée comme suit:

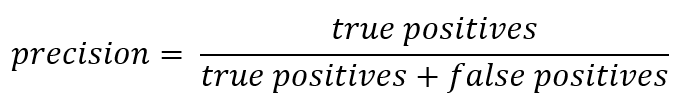
En d'autres termes, il est tenu compte du nombre de réponses positives reçues du classificateur qui sont correctes. Plus la précision est élevée, moins le nombre de faux coups (la précision est de 1 s'il n'y avait pas de FP).

Le rappel est généralement présenté comme:

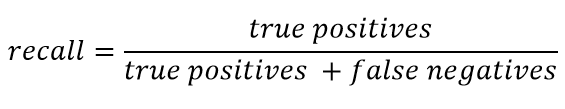
Le rappel caractérise la capacité du classificateur à «deviner» autant de réponses positives que possible. Plus la complétude est élevée, plus le FN est bas.

Habituellement, ils essaient de trouver un équilibre entre les deux, mais dans ce cas, la priorité sera entièrement accordée à la précision. La raison: une approche plus humaniste, le désir de minimiser le nombre de faux positifs et, par conséquent, d'éviter les soupçons tombant sur les innocents.

Nous calculons la précision pour nos classificateurs:

 from sklearn.metrics import precision_score def calculate_precision(X, y): result = pd.DataFrame(columns=['classifier', 'precision']) for clf in classifiers: predicted = clf.predict(X_test) precision = precision_score(y_test, predicted, average='macro') classifier = clf.__class__.__name__ classifier = classifier.replace('Classifier', '') result = result.append({'classifier': classifier, 'precision': precision}, ignore_index=True) print('Precision is {precision} for {classifier_name}'.format(precision=round(precision,2), classifier_name=classifier)) result = result.sort_values(['classifier'], ascending=True) plt.subplots(figsize=(10, 7)) sns.barplot(x="classifier", y='precision', palette=cmap, data=result) calculate_precision(X_train, y_train) 

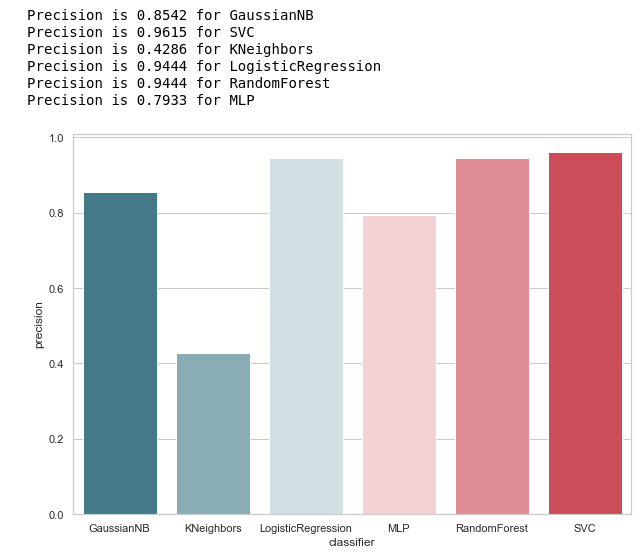
Comme le montre la figure, elle est ressortie comme prévu: la précision KNeighbors s'est avérée être la plus faible, car la valeur TP est la plus faible.

Dans le même temps, il y a un bon article sur les métriques sur le Habré, et ceux qui veulent approfondir ce sujet devraient en prendre connaissance.

Sélection hyper paramètre

Après avoir trouvé la métrique qui convient le mieux aux conditions sélectionnées (nous réduisons le nombre de FP), nous pouvons revenir à la première question: Quelle est la raison de ce comportement du classificateur KNeighbors?

La raison réside dans les paramètres par défaut avec lesquels ce modèle a été créé. Et, très probablement, beaucoup pourraient s'exclamer à ce stade: pourquoi s'entraîner sur les paramètres par défaut? Il existe des outils de sélection spéciaux, par exemple, le GridSearchCV souvent utilisé.
Oui, ça l'est, et le moment est venu d'y recourir,

Mais avant cela, nous supprimons le classificateur bayésien de notre liste. Il autorise un FP, et en même temps, cet algorithme n'accepte aucun paramètre variable, de sorte que le résultat ne changera pas.

 classifiers.remove(gnb) 

Réglage fin

Nous définissons une grille de paramètres pour chaque classificateur:

 parameters = {'SVC':{'kernel':('linear', 'rbf','poly'), 'C':[i for i in range(1,11)],'random_state': (random_state,)}, 'KNeighbors':{'algorithm':('ball_tree', 'kd_tree'), 'n_neighbors':[i for i in range(2,20)]}, 'LogisticRegression':{'penalty':('l1', 'l2'), 'C':[i for i in range(1,11)],'random_state': (random_state,)}, 'RandomForest':{'n_estimators':[i for i in range(10,101,10)],'random_state': (random_state,)}, 'MLP':{'activation':('relu','logistic'),'solver':('sgd','lbfgs'),'max_iter':(500,1000), 'hidden_layer_sizes':[(7,),(7,7)],'random_state': (random_state,)}} 

De plus, je voulais faire attention au nombre de couches / neurones dans MLP.
Il a été décidé de ne pas les définir par une recherche exhaustive de toutes les valeurs possibles, mais toujours en fonction de la formule :

$$$N_h = \ frac {N_s} {(\ alpha * (N_i + N_o))} = \ frac {117} {(2 * (7 + 1))} \ environ 7$

Je veux dire tout de suite, la formation et la validation croisée se feront uniquement sur l'échantillon de formation. Je suppose qu'il existe une opinion selon laquelle vous pouvez le faire sur toutes les données, comme dans l' exemple avec Iris Dataset. Mais, à mon avis, cette approche n'est pas entièrement justifiée, car il ne sera pas possible de faire confiance aux résultats de la vérification sur un échantillon de test.

Nous procéderons à l'optimisation et remplacerons nos classificateurs par leur version améliorée:

 from sklearn.model_selection import GridSearchCV warnings.filterwarnings('ignore') for idx,clf in enumerate(classifiers): classifier = clf.__class__.__name__ classifier = classifier.replace('Classifier', '') params = parameters.get(classifier) if not params: continue new_clf = clf.__class__() gs = GridSearchCV(new_clf, params, cv=5) result =gs.fit(X_train, y_train) print(f'The best params for {classifier} are {result.best_params_}') classifiers[idx] = result.best_estimator_ 

Après avoir choisi une métrique pour l'évaluation et effectué GridSearchCV, nous sommes prêts à tracer la ligne finale.

Pour résumer

Matrice d'erreur v.2

 matrices = make_confussion_matrices(X_train,y_train) draw_confussion_matrices(1,2,first_row,figsize = (10.5,6)) draw_confussion_matrices(1,3,second_row,figsize = (16,6)) 

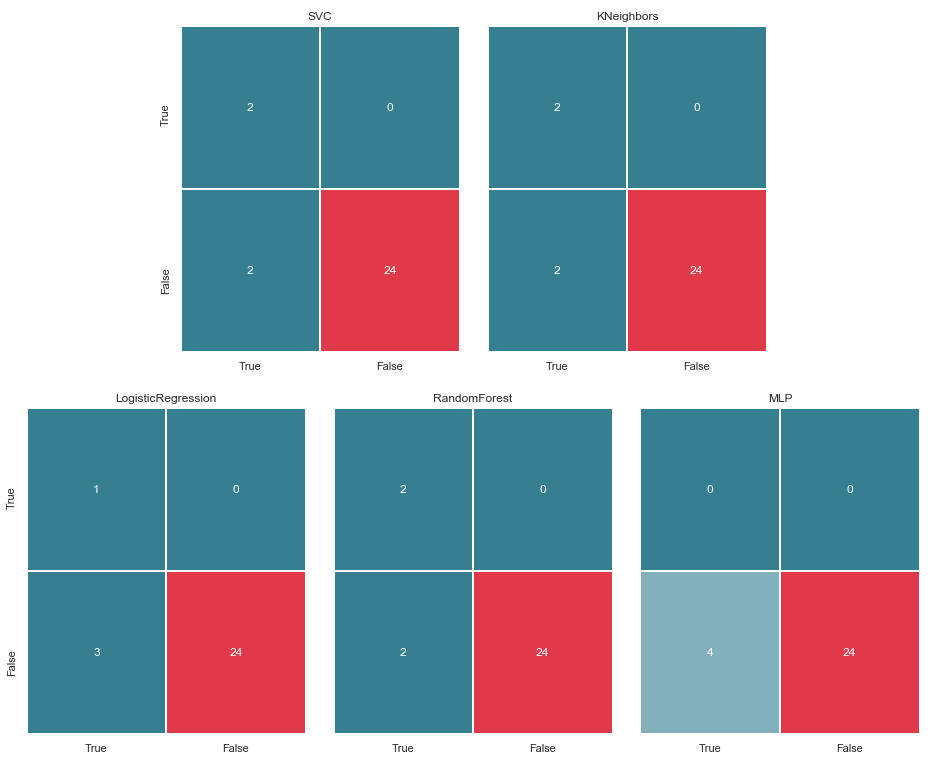
Comme le montre la matrice, le MLP a montré une dégradation et a considéré qu'il n'y avait aucun suspect dans l'échantillon d'essai. Random Forest a gagné en précision et corrigé les paramètres pour les faux négatifs et les vrais positifs. Et KNeighbors a montré une amélioration de la prédiction. Les prévisions pour les autres n'ont pas changé.

Précision v.2

Maintenant, aucun de nos classificateurs actuels n'a d'erreurs avec False Positive, ce qui est une bonne nouvelle. Mais, si nous exprimons tout dans la langue des nombres, nous obtenons l'image suivante:

 calculate_precision(X_train, y_train) 

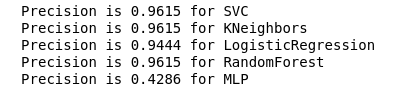
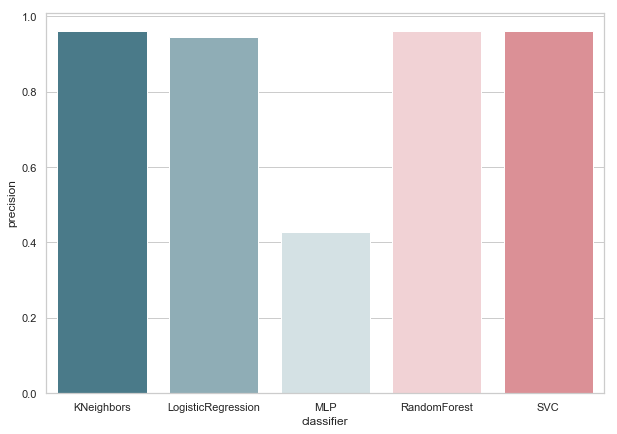
3 classificateurs avec le score de précision le plus élevé ont été identifiés. Et ils ont les mêmes valeurs, basées sur la matrice d'erreur. Quel classificateur choisir?

Qui est meilleur?

Il me semble que c'est une question assez difficile à laquelle il n'y a pas de réponse universelle. Cependant, mon point de vue dans ce cas ressemblerait à ceci:

1. Le classificateur doit être aussi simple que possible dans sa mise en œuvre technique. Ensuite, il aura moins de risques de se recycler (cela est probablement arrivé avec MLP). Par conséquent, ce n'est pas une forêt aléatoire, car cet algorithme est un ensemble de 30 arbres et, par conséquent, en dépend. Conforme à l'une des idées de Python Zen: simple vaut mieux que complexe.

2. Pas mal quand l'algorithme était intuitif. Autrement dit, les voisins KN sont perçus plus simplement que les SVM avec un espace multidimensionnel potentiel.
Qui à son tour est similaire à une autre déclaration: explicite vaut mieux qu'implicite.

Par conséquent, KNeighbors avec 3 voisins, à mon avis, est le meilleur candidat.

Ceci est la fin de la deuxième partie, décrivant l'utilisation d'Enron Dataset comme exemple de la tâche de classification dans l'apprentissage automatique. Basé sur le matériel du cours Introduction à l'apprentissage automatique sur l'Udacity. Il y a aussi un cahier en python reflétant la séquence entière des actions décrites.