Théorie des jeux: prise de décision avec exemples à Kotlin

La théorie des jeux est une discipline mathématique qui considère la modélisation des actions des joueurs qui ont un objectif, qui est de choisir les stratégies optimales de comportement dans un conflit. Sur Habré, ce sujet a déjà été abordé , mais aujourd'hui nous allons parler de certains de ses aspects plus en détail et considérer des exemples sur Kotlin.

Ainsi, une stratégie est un ensemble de règles qui déterminent le choix d'une ligne de conduite pour chaque mouvement personnel, selon la situation. La stratégie optimale du joueur est la stratégie qui garantit la meilleure position dans un jeu donné, c'est-à-dire gain maximum. Si le jeu est répété plusieurs fois et contient, en plus des mouvements personnels et aléatoires, la stratégie optimale fournit le gain moyen maximum.

La tâche de la théorie des jeux est d'identifier les stratégies optimales pour les joueurs. L'hypothèse principale, basée sur les stratégies optimales trouvées, est que l'adversaire (ou les adversaires) n'est pas moins intelligent que le joueur lui-même et fait tout pour atteindre son objectif. Le calcul d'un adversaire raisonnable n'est qu'une des positions potentielles du conflit, mais dans la théorie des jeux c'est lui qui est posé dans les fondements.

Il existe des jeux avec la nature dans lesquels un seul participant maximise ses profits. Les jeux avec la nature sont des modèles mathématiques dans lesquels le choix de la solution dépend de la réalité objective. Par exemple, la demande des consommateurs, l'état de la nature, etc. La «nature» est un concept généralisé d'un adversaire qui ne poursuit pas ses propres objectifs. Dans ce cas, plusieurs critères sont utilisés pour sélectionner la stratégie optimale.
Il existe deux types de tâches dans les jeux avec la nature:

1. la tâche de prendre des décisions dans des conditions de risque lorsque les probabilités avec lesquelles la nature accepte chacun des états possibles sont connues;
2. tâches de décision dans des conditions d'incertitude, lorsqu'il n'est pas possible d'obtenir des informations sur les probabilités d'occurrence d'états de la nature.

Brièvement sur ces critères est décrit ici .

Nous allons maintenant considérer les critères de décision dans les stratégies pures, et à la fin de l'article, nous allons résoudre le jeu dans les stratégies mixtes par la méthode analytique.

Énoncé du problème

Nous analyserons tous les critères de prise de décision à l'aide d'un exemple traversant. La tâche est la suivante: l'agriculteur doit déterminer dans quelles proportions semer son champ avec trois cultures, si le rendement de ces cultures et, par conséquent, le profit, dépendent de la façon dont l'été sera: frais et pluvieux, normal ou chaud et sec. L'agriculteur a calculé le bénéfice net de 1 hectare de différentes cultures en fonction de la météo. Le jeu est déterminé par la matrice suivante:



Nous présenterons ensuite cette matrice sous forme de stratégies:

$$

$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$$

La stratégie optimale souhaitée est indiquée par $$$u_ {opt}$ . Nous allons résoudre le jeu en utilisant les critères Wald, l'optimisme, le pessimisme, Savage et Hurwitz face à l'incertitude et les critères Bayes et Laplace en risque.

Comme mentionné ci-dessus, les exemples seront sur Kotlin. Je note qu'en général, il existe des solutions telles que Gambit (écrit en C), Axelrod et PyNFG (écrit en Python), mais nous roulerons sur notre propre vélo, assemblé sur le genou, juste afin de pousser un peu élégant, à la mode et langage de programmation pour les jeunes.

Pour implémenter par programmation la solution du jeu, nous allons introduire plusieurs classes. Tout d'abord, nous avons besoin d'une classe qui nous permet de décrire une ligne ou une colonne d'une matrice de jeu. La classe est extrêmement simple et contient une liste de valeurs possibles (alternatives ou états de la nature) et leur nom correspondant. Le champ key sera utilisé pour l'identification, ainsi que pour la comparaison, et la comparaison sera nécessaire dans la mise en œuvre de la domination.


La matrice du jeu contient des informations sur les alternatives et les états de la nature. De plus, il implémente certaines méthodes, par exemple, trouver l'ensemble dominant et le prix net du jeu.


Nous décrivons l'interface qui répond aux critères

Prise de décision dans l'incertitude

Prendre des décisions face à l'incertitude suggère que le joueur n'est pas opposé à un adversaire raisonnable.

Critère de Wald

Le critère de Wald maximise le pire résultat possible:

$$

$$u_ {opt} = max_ {i} min_ {j} [U]$$

L'utilisation du critère assure contre le pire résultat, mais le prix d'une telle stratégie est la perte de l'opportunité d'obtenir le meilleur résultat possible.

Prenons un exemple. Pour les stratégies $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ trouver les bas et obtenir les trois prochains $$$S = (0, 1, -1)$ . Le maximum pour le triple indiqué sera la valeur 1, donc, selon le critère de Wald, la stratégie gagnante est la stratégie $$$U_ {2} = (2,3,1)$ correspondant à Plantation Culture 2.

L'implémentation logicielle du critère Wald est simple:

 class WaldCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val max = mins.maxWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == max!!.second } .map { m -> m.first } } } 

Par souci de clarté, pour la première fois, je montrerai à quoi ressemblerait la solution comme un test:


Il est facile de deviner que pour d'autres critères, la différence ne sera que dans la création de l'objet criteria .

Critère d'optimisme

Lorsqu'il utilise le critère d'un optimiste, le joueur choisit une solution qui donne le meilleur résultat, tandis que l'optimiste suppose que les conditions de jeu lui seront les plus favorables:

$$

$$u_ {opt} = max_ {i} max_ {j} [U]$$

La stratégie d’un optimiste peut entraîner des conséquences négatives lorsque l’offre maximale coïncide avec la demande minimale - l’entreprise peut subir des pertes lors de la radiation de produits invendus. Dans le même temps, la stratégie de l'optimiste a une certaine signification, par exemple, vous n'avez pas besoin de prendre soin des clients insatisfaits, car toute demande possible est toujours satisfaite, il n'est donc pas nécessaire de maintenir l'emplacement des clients. Si la demande maximale est réalisée, la stratégie de l'optimiste vous permet d'obtenir une utilité maximale tandis que d'autres stratégies entraîneront une perte de profits. Cela donne certains avantages concurrentiels.

Prenons un exemple. Pour les stratégies $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ trouver, trouver le maximum et obtenir les trois prochains $$$S = (5, 3, 4)$ . Le maximum pour le triple indiqué sera la valeur 5, donc, selon le critère d'optimisme, la stratégie gagnante est la stratégie $$$U_ {1} = (0,2,5)$ correspondant à Plantation Culture 1.

La mise en œuvre du critère d'optimisme n'est pratiquement pas différente du critère de Wald:

 class WaldCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val max = mins.maxWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == max!!.second } .map { m -> m.first } } } 

Critère de pessimisme

Ce critère est destiné à sélectionner le plus petit élément de la matrice de jeu parmi ses éléments minimum possibles:

$$

$$u_ {opt} = min_ {i} min_ {j} [U]$$

Le critère du pessimisme suggère que l'évolution des événements sera défavorable au décideur. En utilisant ce critère, le décideur est guidé par la possible perte de contrôle de la situation, il essaie donc d'exclure les risques potentiels en choisissant l'option avec une rentabilité minimale.

Prenons un exemple. Pour les stratégies $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ trouver, trouver le minimum et obtenir les trois prochains $$$S = (0, 1, -1)$ . Le minimum pour le triple indiqué sera la valeur -1, donc, selon le critère du pessimisme, la stratégie gagnante est la stratégie $$$U_ {3} = (4.3, -1)$ correspondant à Plantation Culture 3.

Après avoir pris connaissance des critères et de l'optimisme de Wald, il est facile de deviner à quoi ressemblera la classe du critère de pessimisme:

 class PessimismCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val min = mins.minWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == min!!.second } .map { m -> m.first } } } 

Critère sauvage

Le critère Savage (critère d'un pessimiste pessimiste) implique de minimiser les plus grands profits perdus, en d'autres termes, le plus grand regret pour les profits perdus est minimisé:

$$

$$u_ {opt} = min_ {i} max_ {j} [S] \\ s_ {i, j} = (max \ begin {bmatrix} u_ {1, j} \\ u_ {2, j} \\. .. \\ u_ {n, j} \ end {bmatrix} - u_ {i, j})$$

Dans ce cas, S est la matrice des regrets.

La solution optimale selon le critère Savage devrait donner le moins de regrets aux regrets trouvés à l'étape précédente. La solution correspondant à l'utilitaire trouvé sera optimale.

Les caractéristiques de la solution obtenue incluent une absence garantie des plus grandes déceptions et une diminution garantie des gains maximums possibles des autres joueurs.

Prenons un exemple. Pour les stratégies $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ faire une matrice de regrets:



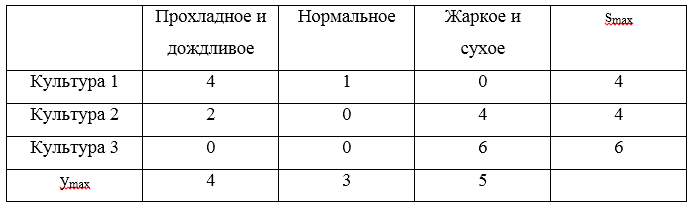
Trois regrets maximum $$$S = (4,4,6)$ . La valeur minimale de ces risques sera une valeur de 4, ce qui correspond aux stratégies $$$U_ {1}$ et $$$U_ {2}$ .

La programmation du test Savage est un peu plus difficile:

 class SavageCriteria(gameMatrix: GameMatrix) : ICriteria { val gameMatrix: GameMatrix init { this.gameMatrix = gameMatrix } fun GameMatrix.risk(): List<Pair<GameVector, Double?>> { val maxStates = this.natureStates.map { n -> Pair(n, n.values.max()) } .map { n -> n.first.key to n.second }.toMap() var am: MutableList<Pair<GameVector, List<Double>>> = mutableListOf() for (a in this.alternatives) { var v: MutableList<Double> = mutableListOf() for (i in 0..a.values.lastIndex) { val mn = maxStates.get(i) v.add(mn!! - a.values[i]) } am.add(Pair(a, v.toList())) } return am.map { m -> Pair(m.first, m.second.max()) } } override fun optimum(): List<GameVector> { val risk = gameMatrix.risk() val minRisk = risk.minWith(Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!) }) return risk .filter { r -> r.second == minRisk!!.second } .map { m -> m.first } } } 

Critère de Hurwitz

Le critère de Hurwitz est un compromis régulé entre pessimisme extrême et optimisme complet:

$$

$$u_ {opt} = max (\ gamma × A (k) + A (0) × (1 - \ gamma))$$

A (0) est la stratégie de l'extrême pessimiste, A (k) est la stratégie de l'optimiste complet, $$$\ gamma = 1$ - valeur de consigne du coefficient de poids: $$$0 \ leq \ gamma \ leq1$ ; $$$\ gamma = 0$ - pessimisme extrême, $$$\ gamma = 1$ - optimisme total.

Avec un petit nombre de stratégies discrètes, définir la valeur souhaitée du coefficient de poids $$$\ gamma$ , puis arrondissez le résultat à la valeur la plus proche possible, en tenant compte de la discrétisation effectuée.

Prenons un exemple. Pour les stratégies $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ . Nous supposons que le coefficient d'optimisme $$$\ gamma = 0,6$ . Faites maintenant un tableau:



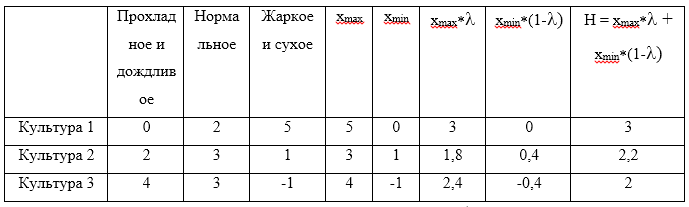
La valeur maximale à partir du H calculé sera la valeur 3, ce qui correspond à la stratégie $$$U_ {1}$ .

La mise en œuvre du critère Hurwitz est déjà plus volumineuse:

 class HurwitzCriteria(gameMatrix: GameMatrix, optimisticKoef: Double) : ICriteria { val gameMatrix: GameMatrix val optimisticKoef: Double init { this.gameMatrix = gameMatrix this.optimisticKoef = optimisticKoef } inner class HurwitzParam(xmax: Double, xmin: Double, optXmax: Double){ val xmax: Double val xmin: Double val optXmax: Double val value: Double init{ this.xmax = xmax this.xmin = xmin this.optXmax = optXmax value = xmax * optXmax + xmin * (1 - optXmax) } } fun GameMatrix.getHurwitzParams(): List<Pair<GameVector, HurwitzParam>> { return this.alternatives.map { a -> Pair(a, HurwitzParam(a.max()!!, a.min()!!, optimisticKoef)) } } override fun optimum(): List<GameVector> { val hpar = gameMatrix.getHurwitzParams() val maxHurw = hpar.maxWith(Comparator { o1, o2 -> o1.second.value.compareTo(o2.second.value) }) return hpar .filter { r -> r.second == maxHurw!!.second } .map { m -> m.first } } } 

Prise de décision à risque

Les méthodes de prise de décision peuvent s'appuyer sur des critères de décision dans des conditions de risque, sous réserve des conditions suivantes:

• manque d'informations fiables sur les conséquences possibles;
• la présence de distributions de probabilité;
• connaissance de la probabilité de résultats ou de conséquences pour chaque décision.

Si une décision est prise dans des conditions de risque, les coûts des décisions alternatives sont décrits par des distributions de probabilité. À cet égard, la décision est basée sur l'utilisation du critère de la valeur attendue, selon lequel les solutions alternatives sont comparées en termes de maximisation des bénéfices attendus ou de minimisation des coûts attendus.

Le critère de la valeur attendue peut être réduit soit pour maximiser le profit attendu (moyen), soit pour minimiser les coûts attendus. Dans ce cas, on suppose que le profit (coûts) associé à chaque solution alternative est une variable aléatoire.

La formulation de ces tâches est généralement la suivante: une personne choisit n'importe quelle action dans une situation où des événements aléatoires influencent le résultat de l'action. Mais le joueur a une certaine connaissance des probabilités de ces événements et peut calculer la combinaison et la séquence les plus rentables de ses actions.

Afin de continuer à donner des exemples, nous complétons la matrice de jeu avec des probabilités:



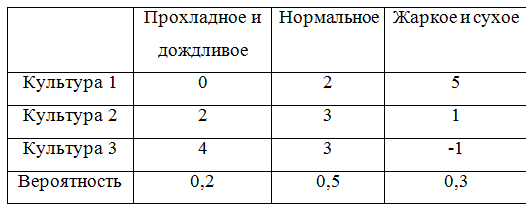
Afin de prendre en compte les probabilités, une classe décrivant la matrice de jeu devra être refaite un peu. Il s'est avéré, en vérité, pas très élégant, mais bon.

Critère de Bayes

Le critère de Bayes (critère d'attente) est utilisé dans les problèmes de prise de décision dans les conditions de risque comme une évaluation de la stratégie $$$u_ {i}$ l'attente mathématique de la variable aléatoire correspondante apparaît. Selon cette règle, la stratégie optimale du joueur $$$u_ {opt}$ se trouve à partir de la condition:

$$

$$u_ {opt} = max_ {1 \ leq i \ leq n} M (u_ {i}) \\ M (u_ {i}) = max_ {1 \ leq i \ leq n} \ sum_ {j = 1} ^ m u_ {i, j} \ cdot y_ {j} ^ 0$$

En d'autres termes, un indicateur d'inefficacité de la stratégie $$$u_ {i}$ par critère de Bayes concernant les risques est la valeur moyenne (attente) des risques de la i-ème ligne de la matrice $$$U$ dont les probabilités coïncident avec les probabilités de la nature. Ensuite, la stratégie optimale parmi les stratégies pures selon le critère de Bayes concernant les risques est la stratégie $$$u_ {opt}$ ayant une inefficacité minimale, c'est-à-dire un risque moyen minimal. Le critère bayésien est équivalent en termes de gains et de risques, c'est-à-dire si la stratégie $$$u_ {opt}$ est optimal par le critère de Bayes en ce qui concerne les victoires, puis il est optimal par le critère de Bayes en ce qui concerne les risques, et vice versa.

Passons à l'exemple et calculons les attentes mathématiques:

$$

$$M_1 = 0 \ cdot0.2 +2 \ cdot0.5 +5 \ cdot0.3 = 2.5; \\ M_2 = 2 \ cdot0.2 +3 \ cdot0.5 +1 \ cdot0.3 = 2.2 ; \\ M_4 = 0 \ cdot0.2 +3 \ cdot0.5 + (- 1) \ cdot0.3 = 2.0;$$

L'espérance mathématique maximale est $$$M_1$ par conséquent, une stratégie gagnante est une stratégie $$$U_1$ .

Implémentation logicielle du critère de Bayes:

 class BayesCriteria(gameMatrix: ProbabilityGameMatrix) : ICriteria { val gameMatrix: ProbabilityGameMatrix init { this.gameMatrix = gameMatrix } fun ProbabilityGameMatrix.bayesProbability(): List<Pair<GameVector, Double?>> { var am: MutableList<Pair<GameVector, Double>> = mutableListOf() for (a in this.alternatives) { var alprob: Double = 0.0 for (i in 0..a.values.lastIndex) { alprob += a.values[i] * this.probabilities[i] } am.add(Pair(a, alprob)) } return am.toList(); } override fun optimum(): List<GameVector> { val risk = gameMatrix.bayesProbability() val maxBayes = risk.maxWith(Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!) }) return risk .filter { r -> r.second == maxBayes!!.second } .map { m -> m.first } } } 

Critère de Laplace

Le critère de Laplace présente une maximisation simplifiée de l'attente mathématique d'utilité lorsque l'hypothèse d'une probabilité égale de niveaux de demande est valide, ce qui élimine la nécessité de collecter des statistiques réelles.

Dans le cas général, lors de l'utilisation du critère de Laplace, la matrice des utilités attendues et le critère optimal sont déterminés comme suit:

$$

$$u_ {opt} = max [\ overline {U}] \\ \ overline {U} = \ begin {bmatrix} \ overline {u} _ {1} \\ \ overline {u} _ {2} \\. .. \\ \ overline {u} _ {n} \ end {bmatrix}, \ overline {u} _ {i} = \ frac {1} {n} \ sum_ {j = 1} ^ nu_ {i, j }$$

Prenons l'exemple de la prise de décision selon le critère de Laplace. Nous calculons la moyenne arithmétique pour chaque stratégie:

$$

$$\ overline {u} _ {1} = \ frac {1} {3} \ cdot (0 + 2 + 5) = 2.3 \\ \ overline {u} _ {2} = \ frac {1} { 3} \ cdot (2 + 3 + 1) = 2.0 \\ \ overline {u} _ {3} = \ frac {1} {3} \ cdot (4 + 3-1) = $ 2.$$

La stratégie gagnante est donc la stratégie $$$U_1$ .

Implémentation logicielle du critère de Laplace:

 class LaplaceCriteria(gameMatrix: GameMatrix) : ICriteria { val gameMatrix: GameMatrix init { this.gameMatrix = gameMatrix } fun GameMatrix.arithemicMean(): List<Pair<GameVector, Double>> { return this.alternatives.map { m -> Pair(m, m.values.average()) } } override fun optimum(): List<GameVector> { val risk = gameMatrix.arithemicMean() val maxBayes = risk.maxWith(Comparator { o1, o2 -> o1.second.compareTo(o2.second) }) return risk .filter { r -> r.second == maxBayes!!.second } .map { m -> m.first } } } 

Stratégies mixtes. Méthode analytique

La méthode analytique vous permet de résoudre le jeu dans des stratégies mixtes.Afin de formuler un algorithme pour trouver une solution à un jeu par une méthode analytique, nous considérons quelques concepts supplémentaires.

La stratégie$$U i domine la stratégie$U_{i}$$$U i - 1 , si tout$U_{i-1}$$$$u_{1..n} \in U_{i} \geq u_{1..n} \in U_{i-1}$ .En d'autres termes, si dans une ligne d'une matrice de paiement tous les éléments sont supérieurs ou égaux aux éléments correspondants d'une autre ligne, la première ligne domine la seconde et est appelée la ligne dominante. Et aussi si dans une colonne de la matrice de paiement tous les éléments sont inférieurs ou égaux aux éléments correspondants d'une autre colonne, alors la première colonne domine la seconde et est appelée la colonne dominante.

Le prix le plus bas du jeu est appelé$$$\alpha = max_i min_j u_{ij}$ .
Le prix le plus élevé du jeu est appelé $$$\beta = min_j max_i u_{ij}$ .

Vous pouvez maintenant formuler un algorithme pour résoudre le jeu par la méthode analytique:

1. Calculer le fond $$α et supérieur$\alpha$$$Prix ​​du jeu β .$\beta$ Si $$α = β , puis écrivez la réponse en stratégies pures; sinon, continuez la solution plus loin$\alpha = \beta$
2. Supprimer les lignes dominantes des colonnes dominantes. Il peut y en avoir plusieurs. À leur place dans la stratégie optimale, les composantes correspondantes seront 0
3. Résolvez le jeu matriciel par programmation linéaire.

Pour donner un exemple, vous devez donner une classe qui décrit la solution


Et la classe qui exécute la solution par la méthode simplex. Comme je ne comprends pas les mathématiques, j'ai utilisé l'implémentation prête à l'emploi d' Apache Commons Math


Maintenant, nous exécutons la solution par la méthode analytique. Pour plus de clarté, nous prenons une autre matrice de jeu:

$$

$$\begin{pmatrix} 2& 4& 8& 5 \\ 6& 2& 4& 6\\ 3& 2& 5& 4 \end{pmatrix}$$

Il y a un ensemble dominant dans cette matrice:
$$\begin{pmatrix} 2& 4\\ 6& 2\end{pmatrix}$$

Solution de jeu $$( 0 , 33 ; 0 , 67 ; 0 ) avec le prix du jeu égal à 3,33$(0,33; 0,67; 0)$

Au lieu d'une conclusion

J'espère que cet article sera utile à ceux qui ont besoin d'une première approximation avec la solution des jeux avec la nature. Au lieu de conclusions, un lien vers GitHub .

Je serais reconnaissant pour la rétroaction constructive!