Bonjour, Habr! Je vous présente la première page des bandits multi-bras Solving: une comparaison de l'échantillonnage epsilon-greedy et Thompson .

Le problème des bandits armés

Le problème des bandits à plusieurs bras est l'une des tâches les plus fondamentales de la science des solutions. A savoir, c'est le problème de l'allocation optimale des ressources dans des conditions d'incertitude. Le nom de «bandit multi-armé» lui-même vient de vieilles machines à sous contrôlées par des poignées. Ces fusils d'assaut étaient surnommés «bandits», car après leur avoir parlé, les gens se sentaient généralement volés. Imaginez maintenant qu'il existe plusieurs machines de ce type et que les chances de gagner contre différentes voitures sont différentes. Depuis que nous avons commencé à jouer avec ces machines, nous voulons déterminer quelle chance est la plus élevée et utiliser cette machine plus souvent que les autres.

Le problème est le suivant: comment pouvons-nous mieux comprendre quelle machine est la mieux adaptée et en même temps essayer de nombreuses fonctionnalités en temps réel? Ce n'est pas une sorte de problème théorique, c'est un problème auquel une entreprise est confrontée tout le temps. Par exemple, une entreprise dispose de plusieurs options pour les messages qui doivent être affichés aux utilisateurs (par exemple, les messages incluent des publicités, des sites, des images) afin que les messages sélectionnés maximisent une certaine tâche commerciale (conversion, cliquabilité, etc.)

Une façon typique de résoudre ce problème consiste à exécuter plusieurs fois les tests A / B. C'est-à-dire, pendant plusieurs semaines, pour montrer chacune des options également souvent, puis, sur la base de tests statistiques, décider quelle option est la meilleure. Cette méthode convient quand il y a peu d'options, disons 2 ou 4. Mais quand il y a beaucoup d'options, cette approche devient inefficace - à la fois en temps perdu et en perte de profit.

La provenance du temps perdu doit être facile à comprendre. Plus d'options - plus de tests A / B sont nécessaires - plus de temps est nécessaire pour prendre une décision. La survenance de profits perdus n'est pas si évidente. Perte d'opportunité (coût d'opportunité) - les coûts associés au fait qu'au lieu d'une action, nous avons effectué une autre, c'est-à-dire, c'est ce que nous avons perdu en investissant dans A au lieu de B. Investir dans B est le manque à gagner de l'investissement en A. Idem avec vérification des options. Les tests A / B ne doivent pas être interrompus tant qu'ils ne sont pas terminés. Cela signifie que l'expérimentateur ne sait pas quelle option est meilleure jusqu'à la fin des tests. Cependant, on pense toujours qu'une option sera meilleure que l'autre. Cela signifie qu'en prolongeant les tests A / B, nous ne montrons pas les meilleures options pour un nombre suffisamment important de visiteurs (bien que nous ne sachions pas quelles options ne sont pas les meilleures), perdant ainsi nos bénéfices. C'est l'avantage perdu des tests A / B. S'il n'y a qu'un seul test A / B, alors le profit perdu n'est peut-être pas du tout grand. Un grand nombre de tests A / B signifie que pendant longtemps nous devons montrer aux clients beaucoup des meilleures options. Il serait préférable que vous puissiez rapidement éliminer les mauvaises options en temps réel, et seulement alors, s'il reste peu d'options, utilisez des tests A / B pour elles.

Les échantillonneurs ou agents sont des moyens de tester et d'optimiser rapidement la distribution des options. Dans cet article, je vais vous présenter l' échantillonnage de Thompson et ses propriétés. Je comparerai également l'échantillonnage de Thompson avec l'algorithme epsilon-greedy, une autre option populaire pour le problème des bandits à plusieurs bras. Tout sera implémenté en Python à partir de zéro - tout le code peut être trouvé ici .

Bref dictionnaire de concepts

Agent, échantillonneur, bandit ( agent, échantillonneur, bandit ) - un algorithme qui décide quelles options afficher.
Variante - une variante différente du message que le visiteur voit.
Action - l'action que l'algorithme a choisie (quelle option afficher).
Utiliser ( exploiter ) - faites un choix pour maximiser la récompense totale en fonction des données disponibles.
Explorez, explorez - faites des choix pour mieux comprendre le retour sur investissement de chaque option.
Récompense, points ( score, récompense ) - une tâche commerciale, par exemple, la conversion ou la cliquabilité. Pour simplifier, nous pensons qu'il est distribué binomialement et est égal à 1 ou 0 - cliqué ou non.
Environnement - le contexte dans lequel l'agent opère - les options et leur «retour sur investissement» cachés pour l'utilisateur.
Remboursement, probabilité de succès ( taux de versement ) - une variable cachée égale à la probabilité d'obtenir un score = 1, pour chaque option, elle est différente. Mais l'utilisateur ne la voit pas.
Essayez ( essai ) - l'utilisateur visite la page.
Le regret est la différence entre ce qui serait le meilleur résultat de toutes les options disponibles et ce qui était le résultat de l'option disponible dans la tentative actuelle. Moins on regrette les actions déjà prises, mieux c'est.
Message ( message ) - une bannière, une option de page et plus encore, différentes versions dont nous voulons essayer.
Échantillonnage - la génération d'un échantillon à partir d'une distribution donnée.

Explorer et exploiter

Les agents sont des algorithmes qui recherchent une approche de la prise de décision en temps réel afin d'atteindre un équilibre entre l'exploration de l'espace des options et l'utilisation de la meilleure option. Cet équilibre est très important. L'espace des options doit être étudié afin d'avoir une idée de quelle option est la meilleure. Si nous découvrons d'abord cette option la plus optimale, puis que nous l'utilisons tout le temps, nous maximiserons la récompense totale qui nous est offerte par l'environnement. D'un autre côté, nous voulons également explorer d'autres options possibles - et si elles se révélaient meilleures à l'avenir, mais nous ne le savons tout simplement pas encore? En d'autres termes, nous voulons nous assurer contre les pertes possibles, en essayant d'expérimenter un peu avec des options sous-optimales afin de clarifier par elles-mêmes leur retour sur investissement. Si leur retour sur investissement est en fait plus élevé, ils peuvent être affichés plus souvent. Un autre avantage des recherches sur les options est que nous pouvons mieux comprendre non seulement le retour sur investissement moyen, mais aussi la répartition approximative du retour sur investissement, c'est-à-dire que nous pouvons mieux estimer l'incertitude.
Le principal problème est donc de résoudre - quelle est la meilleure façon de sortir du dilemme entre le compromis entre l'exploration et l'exploitation.

Algorithme Epsilon-gourmand

Un moyen typique de sortir de ce dilemme est l'algorithme epsilon-gourmand. «Gourmand» signifie exactement ce que vous pensiez. Après une période initiale, lorsque nous faisons accidentellement des tentatives - disons, 1000 fois, l'algorithme choisit avec empressement la meilleure option k dans e pour cent des tentatives. Par exemple, si e = 0,05, l'algorithme 95% du temps sélectionne la meilleure option, et dans les 5% restants du temps, il sélectionne les tentatives aléatoires. En fait, c'est un algorithme plutôt efficace, cependant, il ne suffit peut-être pas d'explorer l'espace des options, et donc, il ne sera pas suffisant d'évaluer quelle option est la meilleure, de rester bloqué sur une option sous-optimale. Montrons dans le code comment fonctionne cet algorithme.

Mais d'abord, quelques dépendances. Nous devons définir l'environnement. C'est le contexte dans lequel les algorithmes s'exécuteront. Dans ce cas, le contexte est très simple. Il appelle l'agent pour que l'agent décide quelle action choisir, puis le contexte lance cette action et renvoie les points reçus pour cela à l'agent (qui met à jour son état).

class Environment: def __init__(self, variants, payouts, n_trials, variance=False): self.variants = variants if variance: self.payouts = np.clip(payouts + np.random.normal(0, 0.04, size=len(variants)), 0, .2) else: self.payouts = payouts #self.payouts[5] = self.payouts[5] if i < n_trials/2 else 0.1 self.n_trials = n_trials self.total_reward = 0 self.n_k = len(variants) self.shape = (self.n_k, n_trials) def run(self, agent): """Run the simulation with the agent. agent must be a class with choose_k and update methods.""" for i in range(self.n_trials): # agent makes a choice x_chosen = agent.choose_k() # Environment returns reward reward = np.random.binomial(1, p=self.payouts[x_chosen]) # agent learns of reward agent.reward = reward # agent updates parameters based on the data agent.update() self.total_reward += reward agent.collect_data() return self.total_reward

Les points sont distribués binomialement avec une probabilité p dépendant du nombre de l'action (tout comme ils pourraient être distribués en continu, l'essence n'aurait pas changé). Je définirai également la classe BaseSampler - elle est nécessaire uniquement pour stocker les journaux et divers attributs.

 class BaseSampler: def __init__(self, env, n_samples=None, n_learning=None, e=0.05): self.env = env self.shape = (env.n_k, n_samples) self.variants = env.variants self.n_trials = env.n_trials self.payouts = env.payouts self.ad_i = np.zeros(env.n_trials) self.r_i = np.zeros(env.n_trials) self.thetas = np.zeros(self.n_trials) self.regret_i = np.zeros(env.n_trials) self.thetaregret = np.zeros(self.n_trials) self.a = np.ones(env.n_k) self.b = np.ones(env.n_k) self.theta = np.zeros(env.n_k) self.data = None self.reward = 0 self.total_reward = 0 self.k = 0 self.i = 0 self.n_samples = n_samples self.n_learning = n_learning self.e = e self.ep = np.random.uniform(0, 1, size=env.n_trials) self.exploit = (1 - e) def collect_data(self): self.data = pd.DataFrame(dict(ad=self.ad_i, reward=self.r_i, regret=self.regret_i))

Ci-dessous, nous définissons 10 options et récupération pour chacune. La meilleure option est l'option 9 avec un retour sur investissement de 0,11%.

 variants = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] payouts = [0.023, 0.03, 0.029, 0.001, 0.05, 0.06, 0.0234, 0.035, 0.01, 0.11]

Afin d'avoir quelque chose à construire, nous définissons également la classe RandomSampler. Cette classe est nécessaire comme modèle de base. Il choisit simplement au hasard une option à chaque tentative et ne met pas à jour ses paramètres.

 class RandomSampler(BaseSampler): def __init__(self, env): super().__init__(env) def choose_k(self): self.k = np.random.choice(self.variants) return self.k def update(self): # nothing to update #self.thetaregret[self.i] = self.thetaregret[self.i] #self.regret_i[self.i] = np.max(self.thetaregret) - self.theta[self.k] #self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.theta) - self.theta[self.k] self.a[self.k] += self.reward self.b[self.k] += 1 self.theta = self.a/self.b self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1

D'autres modèles ont la structure suivante. Tous ont des méthodes choose_k et update. choose_k implémente la méthode par laquelle l'agent sélectionne une option. update met à jour les paramètres de l'agent - cette méthode caractérise comment la capacité de l'agent à choisir l'option change (avec RandomSampler, cette capacité ne change en rien). Nous exécutons l'agent dans l'environnement en utilisant le modèle suivant.

 en0 = Environment(machines, payouts, n_trials=10000) rs = RandomSampler(env=en0) en0.run(agent=rs)

L'essence de l'algorithme epsilon-greedy est la suivante.

Sélectionnez aléatoirement k pour n tentatives.
À chaque tentative, pour chaque option, évaluez les gains.
Après toutes les n tentatives:
Avec la probabilité 1 - e choisissez k avec le gain le plus élevé;
Avec la probabilité e, choisissez K au hasard.

Code Epsilon-gourmand:

 class eGreedy(BaseSampler): def __init__(self, env, n_learning, e): super().__init__(env, n_learning, e) def choose_k(self): # e% of the time take a random draw from machines # random k for n learning trials, then the machine with highest theta self.k = np.random.choice(self.variants) if self.i < self.n_learning else np.argmax(self.theta) # with 1 - e probability take a random sample (explore) otherwise exploit self.k = np.random.choice(self.variants) if self.ep[self.i] > self.exploit else self.k return self.k # every 100 trials update the successes # update the count of successes for the chosen machine def update(self): # update the probability of payout for each machine self.a[self.k] += self.reward self.b[self.k] += 1 self.theta = self.a/self.b #self.total_reward += self.reward #self.regret_i[self.i] = np.max(self.theta) - self.theta[self.k] #self.thetaregret[self.i] = self.thetaregret[self.i] self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.thetas) - self.theta[self.k] self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1

Ci-dessous sur le graphique, vous pouvez voir les résultats d'un échantillonnage purement aléatoire, c'est-à-dire qu'il n'y a pas de modèle ici. Le graphique montre quel choix l'algorithme a fait à chaque tentative, s'il y a eu 10 000 tentatives. L'algorithme essaie seulement, mais n'apprend pas. Au total, il a marqué 418 points.

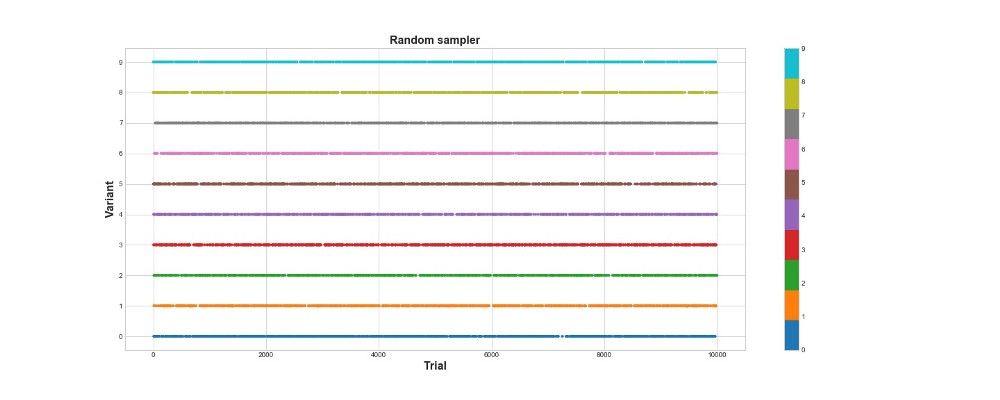
Voyons comment l'algorithme epsilon-greedy se comporte dans le même environnement. Exécutez l'algorithme pour 10 000 tentatives avec e = 0,1 et n_learning = 500 (l'agent essaie simplement les 500 premières tentatives, puis il essaie avec la probabilité e = 0,1). Évaluons l'algorithme en fonction du nombre total de points qu'il marque dans l'environnement.

 en1 = Environment(machines, payouts, n_trials) eg = eGreedy(env=en1, n_learning=500, e=0.1) en1.run(agent=eg)

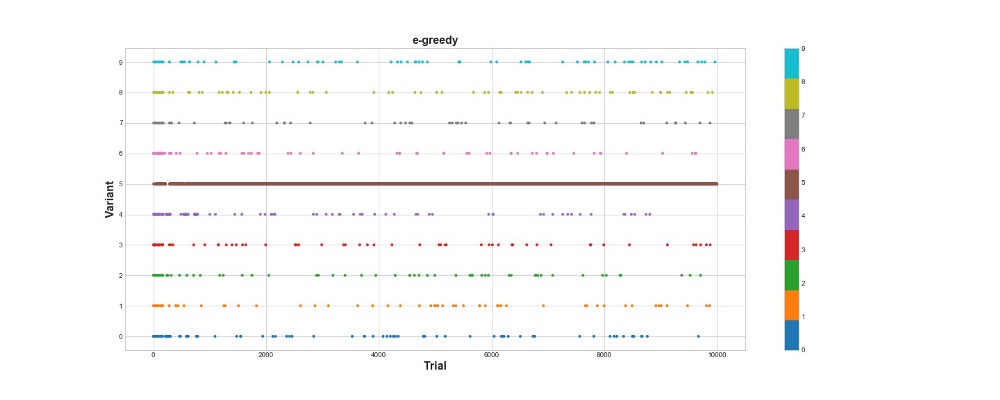
L'algorithme gourmand d'Epsilon a marqué 788 points, près de 2 fois mieux que l'algorithme aléatoire - super! Le deuxième graphique explique assez bien cet algorithme. Nous voyons que pour les 500 premières étapes, les actions sont réparties approximativement également et K est choisi au hasard. Cependant, il commence alors à exploiter fortement l'option 5 - c'est une option assez forte, mais pas la meilleure. Nous constatons également que l'agent sélectionne toujours au hasard 10% du temps.

C'est assez cool - nous n'avons écrit que quelques lignes de code, et maintenant nous avons déjà un algorithme assez puissant qui peut explorer l'espace des options et prendre des décisions presque optimales. En revanche, l'algorithme n'a pas trouvé la meilleure option. Oui, nous pouvons augmenter le nombre d'étapes d'apprentissage, mais de cette façon, nous passerons encore plus de temps sur une recherche aléatoire, ce qui aggravera encore le résultat final. De plus, l'aléatoire est intégré à ce processus par défaut - le meilleur algorithme peut ne pas être trouvé.

Plus tard, je lancerai chacun des algorithmes plusieurs fois afin de pouvoir les comparer les uns par rapport aux autres. Mais pour l'instant, examinons l'échantillonnage de Thompson et testons-le dans le même environnement.

Échantillonnage de Thompson

L'échantillonnage de Thompson est fondamentalement différent de l'algorithme epsilon-greedy par trois points principaux:

Ce n'est pas gourmand.
Il fait des tentatives d'une manière plus sophistiquée.
C'est bayésien.

Le point principal est le paragraphe 3, les paragraphes 1 et 2 en découlent.

L'essence de l'algorithme est la suivante:

Définissez la distribution bêta initiale entre 0 et 1 pour le retour sur investissement de chaque option.
Échantillonnez les options de cette distribution, sélectionnez le paramètre Thêta maximum.
Choisissez l'option k associée à la plus grande thêta.
Voir combien de points ont été marqués, mettre à jour les paramètres de distribution.

En savoir plus sur la distribution bêta ici .
Et à propos de son utilisation en Python - ici .

Code d'algorithme:

  class ThompsonSampler(BaseSampler): def __init__(self, env): super().__init__(env) def choose_k(self): # sample from posterior (this is the thompson sampling approach) # this leads to more exploration because machines with > uncertainty can then be selected as the machine self.theta = np.random.beta(self.a, self.b) # select machine with highest posterior p of payout self.k = self.variants[np.argmax(self.theta)] #self.k = np.argmax(self.a/(self.a + self.b)) return self.k def update(self): #update dist (a, b) = (a, b) + (r, 1 - r) self.a[self.k] += self.reward self.b[self.k] += 1 - self.reward # ie only increment b when it's a swing and a miss. 1 - 0 = 1, 1 - 1 = 0 #self.thetaregret[self.i] = self.thetaregret[self.i] #self.regret_i[self.i] = np.max(self.theta) - self.theta[self.k] self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.thetas) - self.theta[self.k] self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1

La notation formelle de l'algorithme ressemble à ceci.

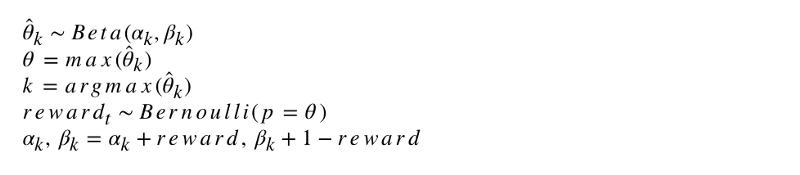
Programmons cet algorithme. Comme d'autres agents, ThompsonSampler hérite de BaseSampler et définit ses propres méthodes choose_k et update. Lancez maintenant notre nouvel agent.

  en2 = Environment(machines, payouts, n_trials) tsa = ThompsonSampler(env=en2) en2.run(agent=tsa)

Comme vous pouvez le voir, il a marqué plus que l'algorithme epsilon-greedy. Super! Regardons le graphique de la sélection des tentatives. On y voit deux choses intéressantes. Premièrement, l'agent a correctement découvert la meilleure option (option 9) et l'a utilisée au maximum. Deuxièmement, l'agent a utilisé d'autres options, mais de manière plus délicate - après environ 1000 tentatives, l'agent, en plus de l'option principale, a principalement utilisé les options les plus puissantes parmi les autres. En d'autres termes, il n'a pas choisi au hasard, mais de manière plus compétente.

Pourquoi ça marche? C'est simple - l'incertitude dans la distribution postérieure des avantages attendus pour chaque option signifie que chaque option est sélectionnée avec une probabilité approximativement proportionnelle à sa forme, déterminée par les paramètres alpha et bêta. En d'autres termes, à chaque tentative, l'échantillonnage de Thompson déclenche l'option en fonction de la probabilité a posteriori qu'il présente l'avantage maximal. En gros, à partir de la distribution des informations sur l'incertitude, l'agent décide quand examiner l'environnement et quand utiliser les informations. Par exemple, une option faible avec une incertitude postérieure élevée peut payer le plus pour cette tentative. Mais pour la plupart des tentatives, plus sa distribution postérieure est forte, plus sa moyenne et son écart-type sont faibles, et donc, plus les chances de le choisir sont grandes.

Autre propriété remarquable de l'algorithme de Thompson: puisqu'il est bayésien, nous pouvons estimer l'incertitude de l'estimation de la rentabilité de chaque option en utilisant ses paramètres. Le graphique ci-dessous montre les distributions postérieures en 6 points différents et en 20 000 tentatives. Vous voyez comment les distributions commencent progressivement à converger vers l'option avec le meilleur retour sur investissement.

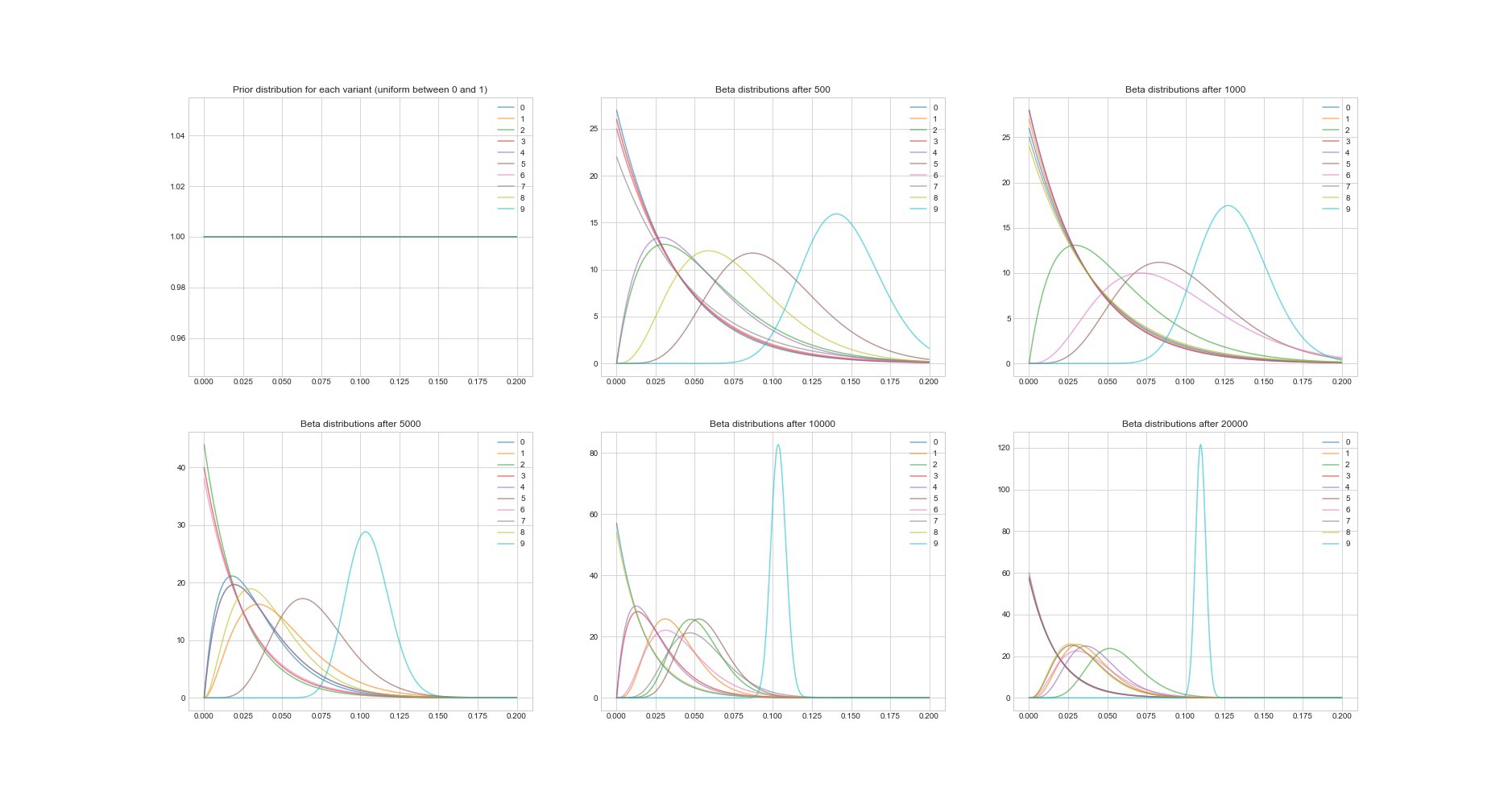
Comparez maintenant les 3 agents dans 100 simulations. 1 simulation est un lancement d'agent sur 10 000 tentatives.

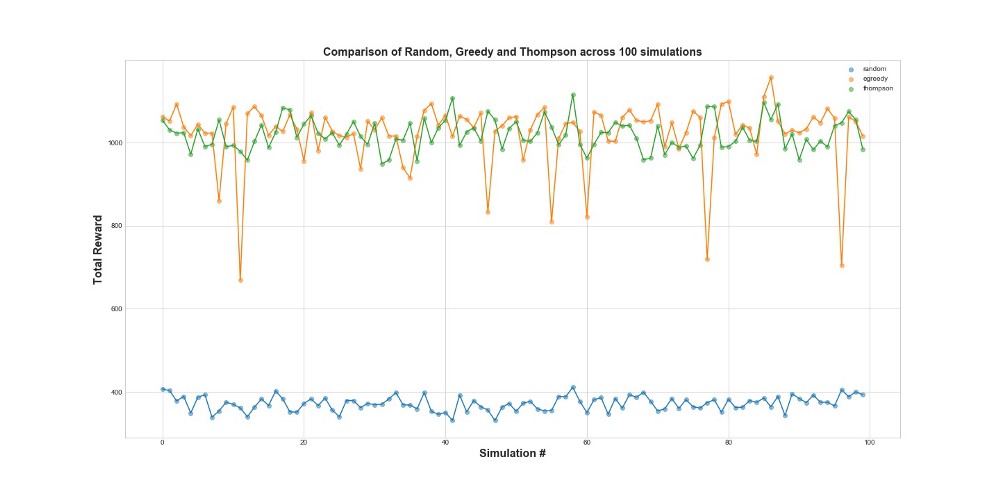
Comme vous pouvez le voir sur le graphique, la stratégie epsilon-greedy et l'échantillonnage de Thompson fonctionnent beaucoup mieux que l'échantillonnage aléatoire. Vous serez peut-être surpris que la stratégie epsilon-greedy et l'échantillonnage de Thompson soient en fait comparables en termes de performances. La stratégie gourmande d'Epsilon peut être très efficace, mais elle est plus risquée, car elle peut rester bloquée sur une option sous-optimale - cela peut être vu dans les échecs du graphique. Mais l'échantillonnage de Thompson ne peut pas, car il fait le choix dans l'espace des options d'une manière plus complexe.

Regret

Une autre façon d'évaluer l'efficacité de l'algorithme est d'évaluer le regret. En gros, plus elle est petite par rapport aux actions déjà entreprises, mieux c'est. Voici un graphique du regret total et du regret de l'erreur. Encore une fois - moins il y a de regrets, mieux c'est.

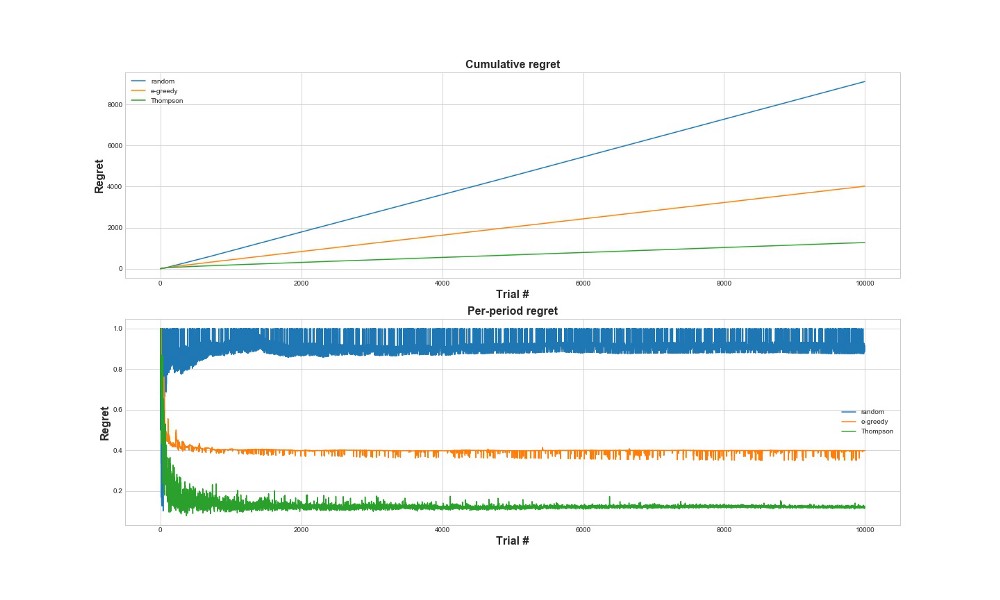
Sur le graphique supérieur, nous voyons le regret total, et sur le regret inférieur la tentative. Comme le montrent les graphiques, l'échantillonnage de Thompson converge vers un regret minimal beaucoup plus rapidement que la stratégie epsilon-cupide. Et il converge vers un niveau inférieur. Avec l'échantillonnage de Thompson, l'agent regrette moins car il peut mieux détecter la meilleure option et mieux essayer les options les plus prometteuses.L'échantillonnage de Thompson est donc particulièrement adapté aux cas d'utilisation plus avancés, tels que les modèles statistiques ou les réseaux de neurones pour choisir k.

Conclusions

Il s'agit d'un poste technique assez long. Pour résumer, nous pouvons utiliser des méthodes d'échantillonnage assez sophistiquées si nous avons de nombreuses options que nous voulons tester en temps réel. L'une des très bonnes caractéristiques de l'échantillonnage de Thompson est qu'il équilibre l'utilisation et l'exploration de manière assez délicate. Autrement dit, nous pouvons le laisser optimiser la distribution des options de solution en temps réel. Ce sont des algorithmes sympas, et ils devraient être plus utiles pour une entreprise que les tests A / B.

Important! L'échantillonnage de Thompson ne signifie pas que vous n'avez pas besoin de faire des tests A / B. Habituellement, ils trouvent d'abord les meilleures options avec son aide, puis font déjà des tests A / B sur eux.

Le problème des bandits à bras multiples - Comparez la stratégie Epsilon-Greedy et l'échantillonnage de Thompson