 Présentation complète de l'apprentissage automatique en Python: deuxième partie
Présentation complète de l'apprentissage automatique en Python: deuxième partieIl peut être difficile de rassembler toutes les parties d'un projet d'apprentissage automatique. Dans cette série d'articles, nous passerons par toutes les étapes de la mise en œuvre du processus d'apprentissage automatique à l'aide de données réelles, et découvrirons comment les différentes techniques sont combinées entre elles.
Dans le
premier article, nous avons nettoyé et structuré les données, effectué une analyse exploratoire, collecté un ensemble d'attributs à utiliser dans le modèle et défini une base de référence pour évaluer les résultats. À l'aide de cet article, nous apprendrons comment implémenter en Python et comparer plusieurs modèles d'apprentissage automatique, effectuer un réglage hyperparamétrique pour optimiser le meilleur modèle et évaluer les performances du modèle final sur un ensemble de données de test.
Tout le code du projet est
sur GitHub , et
voici le deuxième bloc-notes lié à l'article actuel. Vous pouvez utiliser et modifier le code à votre guise!
Évaluation et sélection du modèle
Mémo: Nous travaillons sur une tâche de régression contrôlée, en utilisant
les informations énergétiques des bâtiments de New York pour créer un modèle qui prédit le
score Energy Star qu'un bâtiment particulier recevra. Nous nous intéressons à la fois à l'exactitude des prévisions et à l'interprétabilité du modèle.
Aujourd'hui, vous pouvez choisir parmi les
nombreux modèles d'apprentissage automatique disponibles , et cette abondance peut être intimidante. Bien sûr, il existe
des critiques comparatives sur le réseau qui vous aideront à naviguer lors du choix d'un algorithme, mais je préfère en essayer quelques-unes et voir laquelle est la meilleure. Pour l'essentiel, l'apprentissage automatique est basé sur
des résultats empiriques plutôt que théoriques , et il est presque
impossible de comprendre à l'avance quel modèle est le plus précis .
Il est généralement recommandé de commencer avec des modèles simples et interprétables, tels que la régression linéaire, et si les résultats ne sont pas satisfaisants, passez à des méthodes plus complexes, mais généralement plus précises. Ce graphique (très anti-scientifique) montre la relation entre la précision et l'interprétabilité de certains algorithmes:
 Interprétabilité et précision ( Source ).
Interprétabilité et précision ( Source ).Nous évaluerons cinq modèles de degrés de complexité variables:
- Régression linéaire.
- La méthode des k voisins les plus proches.
- "Forêt aléatoire."
- Augmentation du gradient.
- Méthode des vecteurs de support.
Nous ne considérerons pas l'appareil théorique de ces modèles, mais leur mise en œuvre. Si vous êtes intéressé par la théorie, consultez
An Introduction to Statistical Learning (disponible gratuitement) ou
Hands-On Machine Learning with Scikit-Learn et TensorFlow . Dans les deux livres, la théorie est parfaitement expliquée et l'efficacité de l'utilisation des méthodes mentionnées dans les langages R et Python, respectivement, est montrée.
Remplissez les valeurs manquantes
Bien que lorsque nous avons effacé les données, nous avons supprimé les colonnes dans lesquelles plus de la moitié des valeurs manquent, nous avons encore beaucoup de valeurs. Les modèles d'apprentissage automatique ne peuvent pas fonctionner avec des données manquantes, nous devons donc les
remplir .
Tout d'abord, nous considérons les données et nous rappelons à quoi elles ressemblent:
import pandas as pd import numpy as np
Chaque valeur
NaN est un enregistrement manquant dans les données.
Vous pouvez les remplir de différentes manières , et nous utiliserons la méthode d'imputation médiane assez simple, qui remplace les données manquantes par les valeurs moyennes des colonnes correspondantes.
Dans le code ci-dessous, nous allons créer un
Imputer Imputer
Scikit-Learn avec une stratégie médiane. Ensuite, nous l'
imputer.fit sur les données d'entraînement (en utilisant
imputer.fit ), et l'appliquons pour remplir les valeurs manquantes dans les ensembles d'apprentissage et de test (en utilisant
imputer.transform ). Autrement dit, les enregistrements manquants dans les
données de test seront remplis avec la valeur médiane correspondante
des données d'apprentissage .
Nous effectuons le remplissage et ne formons pas le modèle sur les données tel quel, afin d'éviter le problème de
fuite des données de test lorsque les informations de l'ensemble de données de test entrent dans la formation.
Maintenant que toutes les valeurs sont remplies, il n'y a plus d'espace.
Mise à l'échelle des fonctionnalités
La mise à l'échelle est le processus général de modification de la plage d'une caractéristique.
Il s'agit d'une étape nécessaire , car les signes sont mesurés dans différentes unités, ce qui signifie qu'ils couvrent différentes plages. Cela déforme considérablement les résultats d'algorithmes tels que
la méthode du
vecteur de support et la méthode du plus proche voisin k, qui prennent en compte les distances entre les mesures. Et la mise à l'échelle vous permet d'éviter cela. Bien que des méthodes comme
la régression linéaire et la «forêt aléatoire» ne nécessitent pas de mise à l'échelle des entités, il est préférable de ne pas négliger cette étape lors de la comparaison de plusieurs algorithmes.
Nous mettrons à l'échelle en utilisant chaque attribut dans une plage de 0 à 1. Nous prenons toutes les valeurs de l'attribut, sélectionnons le minimum et le divisons par la différence entre le maximum et le minimum (plage). Cette méthode de mise à l'échelle est souvent appelée
normalisation, et l'autre moyen principal est la normalisation .
Ce processus est facile à implémenter manuellement, nous
MinMaxScaler utiliser l'objet
MinMaxScaler de Scikit-Learn. Le code de cette méthode est identique au code de remplissage des valeurs manquantes, seule la mise à l'échelle est utilisée au lieu de coller. Rappelons que nous apprenons le modèle uniquement sur l'ensemble d'entraînement, puis nous transformons toutes les données.
Désormais, chaque attribut a une valeur minimale de 0 et un maximum de 1. Remplissage des valeurs manquantes et mise à l'échelle des attributs - ces deux étapes sont nécessaires dans presque tous les processus d'apprentissage automatique.
Nous implémentons des modèles d'apprentissage automatique dans Scikit-Learn
Après tous les travaux préparatoires, le processus de création, de formation et d'exécution de modèles est relativement simple. Nous utiliserons la bibliothèque
Scikit-Learn en Python, qui est magnifiquement documentée et avec une syntaxe élaborée pour construire des modèles. En apprenant à créer un modèle dans Scikit-Learn, vous pouvez rapidement implémenter toutes sortes d'algorithmes.
Nous illustrerons le processus de création, de formation (
.fit ) et de test (
.predict ) en utilisant le boost de gradient:
from sklearn.ensemble import GradientBoostingRegressor
Une seule ligne de code pour créer, former et tester. Pour construire d'autres modèles, nous utilisons la même syntaxe, en ne changeant que le nom de l'algorithme.

Afin d'évaluer objectivement les modèles, nous avons calculé le niveau de base en utilisant la valeur médiane de l'objectif et obtenu 24,5. Et les résultats étaient bien meilleurs, donc notre problème peut être résolu en utilisant l'apprentissage automatique.
Dans notre cas, l'
augmentation du gradient (MAE = 10.013) s'est avérée légèrement meilleure que la "forêt aléatoire" (10.014 MAE). Bien que ces résultats ne puissent pas être considérés comme complètement honnêtes, car pour les hyperparamètres, nous utilisons principalement les valeurs par défaut. L'efficacité des modèles dépend fortement de ces paramètres, en
particulier dans la méthode des vecteurs de support . Néanmoins, sur la base de ces résultats, nous choisirons l'augmentation du gradient et commencerons à l'optimiser.
Optimisation de modèle hyperparamétrique
Après avoir choisi un modèle, vous pouvez l'optimiser pour la tâche à résoudre en ajustant les paramètres hyper.
Mais tout d'abord, comprenons
ce que sont les hyperparamètres et comment diffèrent-ils des paramètres ordinaires ?
- Les hyperparamètres du modèle peuvent être considérés comme les paramètres de l'algorithme, que nous avons définis avant le début de sa formation. Par exemple, l'hyperparamètre est le nombre d'arbres dans la "forêt aléatoire" ou le nombre de voisins dans la méthode k-voisins les plus proches.
- Paramètres du modèle - ce qu'elle apprend pendant l'entraînement, par exemple, les poids en régression linéaire.
En contrôlant l'hyperparamètre, nous influençons les résultats du modèle, modifiant l'équilibre entre sa
sous-éducation et sa reconversion . Le sous-apprentissage est une situation où le modèle n'est pas assez complexe (il a trop peu de degrés de liberté) pour étudier la correspondance des signes et des objectifs. Un modèle sous-formé a un biais
élevé , qui peut être corrigé en compliquant le modèle.
Le recyclage est une situation où le modèle se souvient essentiellement des données de formation. Le modèle recyclé présente une variance
élevée , qui peut être ajustée en limitant la complexité du modèle grâce à la régularisation. Les modèles sous-formés et recyclés ne seront pas en mesure de bien généraliser les données de test.
La difficulté de choisir les bons hyperparamètres est que pour chaque tâche, il y aura un ensemble optimal unique. Par conséquent, la seule façon de choisir les meilleurs paramètres est d'essayer différentes combinaisons sur le nouveau jeu de données. Heureusement, Scikit-Learn dispose d'un certain nombre de méthodes qui vous permettent d'évaluer efficacement les hyperparamètres. De plus, des projets comme
TPOT tentent d'optimiser la recherche d'hyperparamètres en utilisant des approches telles que
la programmation génétique . Dans cet article, nous nous limitons à utiliser Scikit-Learn.
Croiser la recherche aléatoire
Implémentons une méthode de réglage hyperparamétrique appelée recherche aléatoire de validation croisée:
- Recherche aléatoire - une technique pour sélectionner les hyperparamètres. Nous définissons une grille, puis sélectionnons au hasard diverses combinaisons à partir de celle-ci, contrairement à la recherche dans la grille, dans laquelle nous essayons successivement chaque combinaison. Soit dit en passant, la recherche aléatoire fonctionne presque aussi bien que la recherche dans la grille , mais beaucoup plus rapidement.
- Le recoupement est un moyen d'évaluer la combinaison sélectionnée d'hyperparamètres. Au lieu de diviser les données en ensembles de formation et de test, ce qui réduit la quantité de données disponibles pour la formation, nous utiliserons la validation croisée k-block (validation croisée K-Fold). Pour ce faire, nous diviserons les données d'apprentissage en k blocs, puis exécuterons le processus itératif, au cours duquel nous formerons d'abord le modèle sur k-1 blocs, puis comparerons le résultat lors de l'apprentissage sur le k-ème bloc. Nous répéterons le processus k fois, et à la fin nous obtiendrons la valeur d'erreur moyenne pour chaque itération. Ce sera l'évaluation finale.
Voici une illustration graphique de la validation croisée du bloc k à k = 5:

L'ensemble du processus de recherche aléatoire de validation croisée ressemble à ceci:
- Nous définissons une grille d'hyperparamètres.
- Sélectionnez au hasard une combinaison d'hyperparamètres.
- Créez un modèle à l'aide de cette combinaison.
- Nous évaluons le résultat du modèle en utilisant la validation croisée k-block.
- Nous décidons quels hyperparamètres donnent le meilleur résultat.
Bien sûr, tout cela ne se fait pas manuellement, mais en utilisant
RandomizedSearchCV de Scikit-Learn!
Nous utiliserons un modèle de régression basé sur l'augmentation du gradient. Il s'agit d'une méthode collective, c'est-à-dire que le modèle se compose de nombreux «apprenants faibles», dans ce cas, à partir d'arbres de décision distincts. Si les élèves apprennent dans des
algorithmes parallèles
comme «forêt aléatoire» , puis que le résultat de la prédiction est sélectionné en votant, puis dans des
algorithmes de renforcement comme le renforcement de gradient, les élèves apprennent en séquence, et chacun d'eux «se concentre» sur les erreurs commises par ses prédécesseurs.
Ces dernières années, les algorithmes de stimulation sont devenus populaires et gagnent souvent dans les compétitions d'apprentissage automatique.
L'amplification du gradient est l'une des implémentations dans lesquelles la descente du gradient est utilisée pour minimiser le coût de la fonction. L'implémentation de l'augmentation de gradient dans Scikit-Learn n'est pas aussi efficace que dans d'autres bibliothèques, par exemple, dans
XGBoost , mais elle fonctionne bien sur de petits ensembles de données et donne des prévisions assez précises.
Retour au réglage hyperparamétrique
Dans la régression utilisant le boosting de gradient, il existe de nombreux hyperparamètres qui doivent être configurés, pour plus de détails, je vous renvoie à la documentation Scikit-Learn. Nous optimiserons:
loss : minimisation de la fonction de perte;n_estimators : nombre d'arbres de décision faibles utilisés (arbres de décision);max_depth : profondeur maximale de chaque arbre de décision;min_samples_leaf : le nombre minimum d'exemples qui devraient être dans le nœud feuille de l'arbre de décision;min_samples_split : le nombre minimum d'exemples nécessaires pour diviser le nœud d'arbre de décision;max_features : nombre maximal de fonctions utilisées pour séparer les nœuds.
Je ne sais pas si quelqu'un comprend vraiment comment tout cela fonctionne, et la seule façon de trouver la meilleure combinaison est d'essayer différentes options.
Dans ce code, nous créons une grille d'hyperparamètres, puis créons un objet
RandomizedSearchCV et recherchons en utilisant une validation croisée à 4 blocs pour 25 combinaisons différentes d'hyperparamètres:
Vous pouvez utiliser ces résultats pour une recherche dans la grille en sélectionnant des paramètres pour la grille qui sont proches de ces valeurs optimales. Mais un réglage ultérieur ne devrait pas améliorer considérablement le modèle. Il existe une règle générale: la construction compétente des fonctionnalités aura un impact beaucoup plus important sur la précision du modèle que le paramètre d'hyperparamètre le plus cher. Il s'agit de la
loi de la baisse de la rentabilité par rapport à l'apprentissage automatique : la conception d'attributs donne le meilleur rendement et le réglage hyperparamétrique n'apporte que des avantages modestes.
Pour modifier le nombre d'estimateurs (arbres de décision) tout en préservant les valeurs des autres hyperparamètres, une expérience peut être effectuée qui démontrera le rôle de ce paramètre. L'implémentation est donnée
ici , mais voici le résultat:
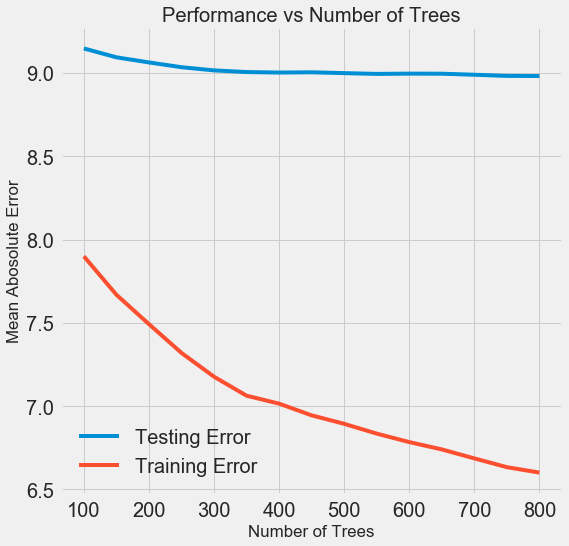
À mesure que le nombre d'arbres utilisés par le modèle augmente, le niveau d'erreurs pendant la formation et les tests diminue. Mais les erreurs d'apprentissage diminuent beaucoup plus rapidement et, par conséquent, le modèle est recyclé: il montre d'excellents résultats sur les données d'entraînement, mais il fonctionne moins bien sur les données de test.
Sur les données de test, la précision diminue toujours (car le modèle voit les bonnes réponses pour le jeu de données d'apprentissage), mais une baisse significative
indique un recyclage . Ce problème peut être résolu en augmentant la quantité de données d'apprentissage ou en
réduisant la complexité du modèle à l'aide d'hyperparamètres . Ici, nous n'aborderons pas les hyperparamètres, mais je vous recommande de toujours faire attention au problème de la reconversion.
Pour notre modèle final, nous prendrons 800 évaluateurs, car cela nous donnera le niveau d'erreur le plus bas dans la validation croisée. Testez maintenant le modèle!
Évaluation à l'aide de données de test
En tant que personnes responsables, nous avons veillé à ce que notre modèle n'ait aucunement accès aux données de test pendant la formation. Par conséquent,
nous pouvons utiliser la précision lorsque nous travaillons avec des données de test comme indicateur de qualité de modèle lorsqu'elles sont admises à des tâches réelles.
Nous alimentons les données de test du modèle et calculons l'erreur. Voici une comparaison des résultats de l'algorithme de renforcement de gradient par défaut et de notre modèle personnalisé:
Le réglage hyperparamétrique a permis d'améliorer la précision du modèle d'environ 10%. Selon la situation, cela peut être une amélioration très importante, mais cela prend beaucoup de temps.
Vous pouvez comparer le temps d'entraînement pour les deux modèles à l'aide de la
%timeit magic
%timeit dans les ordinateurs portables Jupyter. Tout d'abord, mesurez la durée par défaut du modèle:
%%timeit -n 1 -r 5 default_model.fit(X, y) 1.09 s ± 153 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)
Une seconde pour étudier est très décente. Mais le modèle réglé n'est pas si rapide:
%%timeit -n 1 -r 5 final_model.fit(X, y) 12.1 s ± 1.33 s per loop (mean ± std. dev. of 5 runs, 1 loop each)
Cette situation illustre l'aspect fondamental de l'apprentissage automatique:
il s'agit de compromis . Il faut constamment choisir un équilibre entre précision et interprétabilité, entre
déplacement et dispersion , entre précision et durée de fonctionnement, etc. La bonne combinaison est complètement déterminée par la tâche spécifique. Dans notre cas, une augmentation de 12 fois de la durée du travail en termes relatifs est importante, mais en termes absolus, elle est insignifiante.
Nous avons obtenu les résultats finaux des prévisions, analysons-les maintenant et découvrons s'il y a des écarts notables. À gauche, un graphique de la densité des valeurs prédites et réelles, à droite, un histogramme de l'erreur:
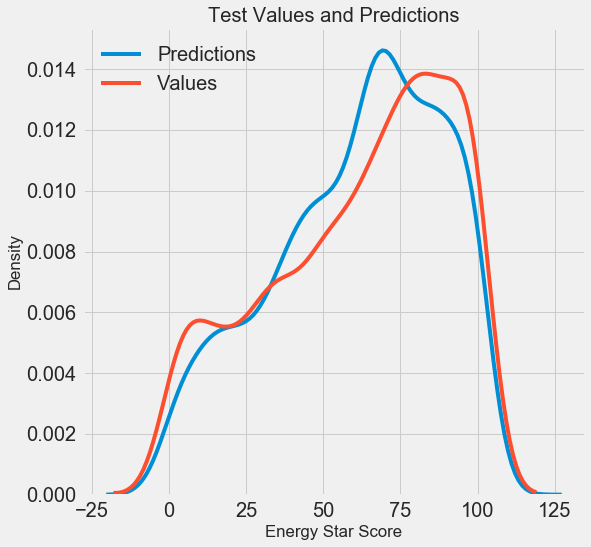

La prévision du modèle répète bien la distribution des valeurs réelles, tandis que sur les données d'apprentissage, le pic de densité est situé plus près de la valeur médiane (66) que du pic de densité réelle (environ 100). Les erreurs ont une distribution presque normale, bien qu'il existe plusieurs grandes valeurs négatives lorsque les prévisions du modèle sont très différentes des données réelles. Dans le prochain article, nous examinerons plus en détail l'interprétation des résultats.
Conclusion
Dans cet article, nous avons examiné plusieurs étapes de la résolution du problème de l'apprentissage automatique:
- Remplissage des valeurs manquantes et des fonctionnalités de mise à l'échelle.
- Évaluation et comparaison des résultats de plusieurs modèles.
- Réglage hyperparamétrique utilisant la recherche aléatoire de grille et la validation croisée.
- Évaluation du meilleur modèle à l'aide de données de test.
Les résultats indiquent que nous pouvons utiliser l'apprentissage automatique pour prédire le score Energy Star sur la base des statistiques disponibles. À l'aide de l'augmentation du gradient, une erreur de 9,1 a été obtenue sur les données de test. Le réglage hyperparamétrique peut grandement améliorer les résultats, mais au prix d'un ralentissement important. C'est l'un des nombreux compromis à considérer dans l'apprentissage automatique.
Dans le prochain article, nous allons essayer de comprendre comment fonctionne notre modèle. Nous examinerons également les principaux facteurs qui influencent le score Energy Star. Si nous savons que le modèle est précis, nous essaierons de comprendre pourquoi il prédit ainsi et ce que cela nous apprend sur le problème lui-même.