L'implémentation d'algorithmes en Python utilisant des calculs symboliques est très pratique pour résoudre des problèmes de modélisation mathématique d'objets définis par des équations différentielles. Pour résoudre de telles équations, les transformées de Laplace sont largement utilisées, ce qui, en termes simplifiés, permet de réduire le problème à la résolution d'équations algébriques simples.
Dans cette publication, je propose d'examiner les fonctions des transformations Laplace directes et inverses de la bibliothèque SymPy, qui vous permettent d'utiliser la méthode Laplace pour résoudre des équations et des systèmes différentiels à l'aide de Python.
La méthode de Laplace elle-même et ses avantages dans la résolution d'équations et de systèmes différentiels linéaires sont largement couverts dans la littérature, par exemple, dans la publication populaire [1]. Dans le livre, la méthode Laplace est présentée pour une implémentation dans des progiciels sous licence Mathematica, Maple et MATLAB (ce qui implique l'achat de ce logiciel par un établissement d'enseignement) en utilisant des exemples sélectionnés par l'auteur.
Aujourd'hui, nous allons essayer de considérer non pas un exemple distinct de résolution d'un problème d'apprentissage en utilisant Python, mais une méthode générale pour résoudre des équations et des systèmes différentiels linéaires en utilisant les fonctions des transformées de Laplace directes et inverses. En même temps, nous économiserons un moment d'apprentissage: le côté gauche de l'équation différentielle linéaire avec les conditions de Cauchy sera formé par l'étudiant lui-même, et la partie de routine de la tâche, consistant en la transformation directe de Laplace du côté droit de l'équation, sera effectuée en utilisant la fonction
laplace_transform () .
L'histoire de la paternité des Laplace transforme
Les transformées de Laplace (images de Laplace) ont une histoire intéressante. Pour la première fois, l'intégrale dans la définition de la transformée de Laplace est apparue dans l'une des œuvres de L. Euler. Cependant, il est généralement admis en mathématiques d'appeler une méthodologie ou un théorème le nom du mathématicien qui l'a découvert après Euler. Sinon, il y aurait plusieurs centaines de théorèmes d'Euler différents.
Dans ce cas, le suivant après Euler était le mathématicien français Pierre Simon de Laplace (Pierre Simon de Laplace (1749-1827)). C'est lui qui a utilisé de telles intégrales dans ses travaux sur la théorie des probabilités. Laplace lui-même n'a pas appliqué les soi-disant «méthodes opérationnelles» pour trouver des solutions d'équations différentielles basées sur les transformées de Laplace (images de Laplace). Ces méthodes ont été découvertes et popularisées par des ingénieurs pratiques, en particulier l'ingénieur électricien anglais Oliver Heaviside (1850-1925). Bien avant que la validité de ces méthodes ne soit rigoureusement prouvée, le calcul opérationnel a été utilisé avec succès et largement, bien que sa légitimité ait été mise en doute dans une large mesure même au début du XXe siècle, et il y avait un débat très acharné sur ce sujet.
Fonctions de la transformée de Laplace directe et inverse
- Fonction de transformation directe de Laplace:
sympy.integrals.transforms. laplace_transform (t, s, ** indices).
La fonction laplace_transform () effectue les transformations de Laplace de la fonction f (t) de la variable réelle en fonction F (s) de la variable complexe, de sorte que:
F ( s ) = i n t ∞ 0 f ( t ) e - s t d t .
Cette fonction renvoie (F, a, cond) , où F (s) est la transformée de Laplace de la fonction f (t) , a <Re (s) est le demi-plan où F (s) est défini, et cond sont des conditions auxiliaires pour la convergence de l'intégrale.
Si l'intégrale ne peut pas être calculée sous forme fermée, cette fonction renvoie un objet LaplaceTransform non calculé.
Si vous définissez l'option noconds = True , la fonction ne renvoie que F (s) . - Fonction de transformation de Laplace inverse:
sympy.integrals.transforms. inverse_laplace_transform (F, s, t, plane = None, ** hints).
La fonction inverse_laplace_transform () effectue la transformation inverse de Laplace de la fonction de la variable complexe F (s) en fonction f (t) de la variable réelle, de sorte que:
f(t)= frac12 pii intc+∞ cdotic−∞ cdotiestF(s)ds.
Si l'intégrale ne peut pas être calculée sous une forme fermée, cette fonction renvoie la InverseLaplaceTransform non appelée de l' objet.
La transformée de Laplace inverse sur l'exemple de la détermination des caractéristiques de transition des régulateurs
La fonction de transfert du contrôleur PID a la forme [2]:
W(s)=(1+ fracKd cdotTd cdots1+Td cdots) cdotKp cdot(1+ frac1Ti cdots) c d o t f r a c 1 s .
Nous allons écrire un programme pour obtenir des équations pour les caractéristiques transitoires des contrôleurs PID et PI pour la fonction de transfert réduit, et dériver en outre le temps passé sur la transformée visuelle de Laplace inverse.
Nous obtenons:Temps de transformation inverse de Laplace visuelle: 2,68 s
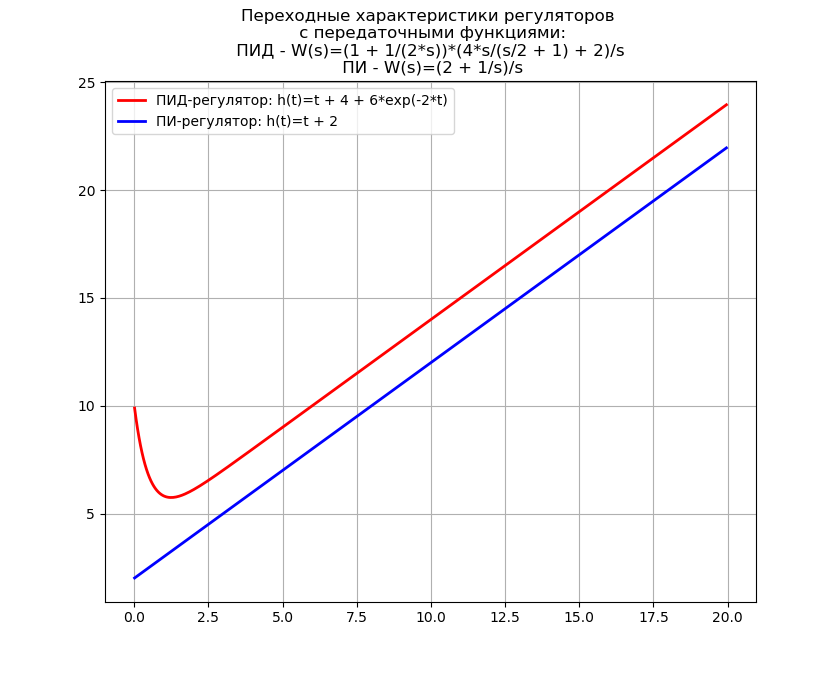
La transformation inverse de Laplace est souvent utilisée dans la synthèse des canons automoteurs, où Python peut remplacer des «monstres» logiciels coûteux comme MathCAD, de sorte que l'utilisation ci-dessus de la transformation inverse est d'une importance pratique.
Transformation de Laplace à partir de dérivées d'ordres supérieurs pour résoudre le problème de Cauchy
Notre discussion se poursuivra avec l'application des transformées de Laplace (images de Laplace) à la recherche de solutions d'une équation différentielle linéaire à coefficients constants de la forme:
a cdotx″(t)+b cdotx′(t)+c cdotx(t)=f(t).(1)
Si
a et
b sont des constantes, alors
L \ left \ {a \ cdot f (t) + b \ cdot q (t) \ right \} = a \ cdot L \ left \ {f (t) \ right \} + b \ cdot L \ left \ {q (t) \ droite \} (2)
pour tous
s tels que les deux transformées de Laplace (image de Laplace) des fonctions
f (t) et
q (t) existent.
Vérifions la linéarité des transformées de Laplace directes et inverses en utilisant les fonctions précédemment considérées
laplace_transform () et
inverse_laplace_transform () . Pour cela, nous prenons
f (t) = sin (3t) ,
q (t) = cos (7t) ,
a = 5 ,
b = 7 comme exemple, et utilisons le programme suivant.
Texte du programme from sympy import* var('sa b') var('t', positive=True) a = 5 f = sin(3*t) b = 7 q = cos(7*t)
Nous obtenons:(7 * s ** 3 + 15 * s ** 2 + 63 * s + 735) / ((s ** 2 + 9) * (s ** 2 + 49))
(7 * s ** 3 + 15 * s ** 2 + 63 * s + 735) / ((s ** 2 + 9) * (s ** 2 + 49))
Vrai
5 * sin (3 * t) + 7 * cos (7 * t)
5 * sin (3 * t) + 7 * cos (7 * t)
Le code ci-dessus démontre également l'unicité de la transformée de Laplace inverse.
En supposant que
q(t)=f′(t) satisfait aux conditions du premier théorème, il s'ensuit de ce théorème que:
L \ left \ {f '' (t) \ right \} = L \ left \ {q '(t) \ right \} = sL \ left \ {q (t) \ right \} - q (0) = sL \ left \ {f '(t) \ right \} - f' (0) = s \ left [sL \ left \ {f (t) -f (0) \ right \} \ right],
et donc
L \ left \ {f '' (t) \ right \} = s ^ {2} \ cdot F (s) -s \ cdot f (0) -f '(0).
La répétition de ce calcul donne
L \ left \ {f '' '(t) \ right \} = sL \ left \ {f' '(t) \ right \} - f' '(0) = s ^ {3} F (s) -s ^ {2} f (0) -sf '(0) -f' '(0).
Après un nombre fini de telles étapes, nous obtenons la généralisation suivante du premier théorème:
L \ left \ {f ^ {(n)} (t) \ right \} = s ^ {n} L \ left \ {f (t) \ right \} - s ^ {n-1} f (0 ) -s ^ {n-2} f '(0) - \ cdot \ cdot \ cdot -f ^ {(n-1)} (0) =
=snF(s)−sn−1f(0)− cdot cdot cdot−sf(n−2)(0)−f(n−1)(0).(3)
En appliquant la relation (3), contenant les dérivés transformés de Laplace de la fonction souhaitée avec les conditions initiales, à l'équation (1), nous pouvons obtenir sa solution selon la méthode spécialement développée dans notre département avec le soutien actif de
Scorobey pour la bibliothèque SymPy.
Une méthode pour résoudre des équations différentielles linéaires et des systèmes d'équations basés sur des transformées de Laplace en utilisant la bibliothèque SymPy
Pour démontrer la méthode, nous utilisons une équation différentielle simple qui décrit le mouvement d'un système constitué d'un point matériel d'une masse donnée, monté sur un ressort auquel une force externe est appliquée. L'équation différentielle et les conditions initiales d'un tel système ont la forme:
x″+4x= sin(3t);x(0)=1,2;x′(0)=1,(4)
où
x(0) - position initiale réduite de la masse,
x′(0) - vitesse de masse initiale réduite.
Un modèle physique simplifié défini par l'équation (4) avec des conditions initiales non nulles [1]:
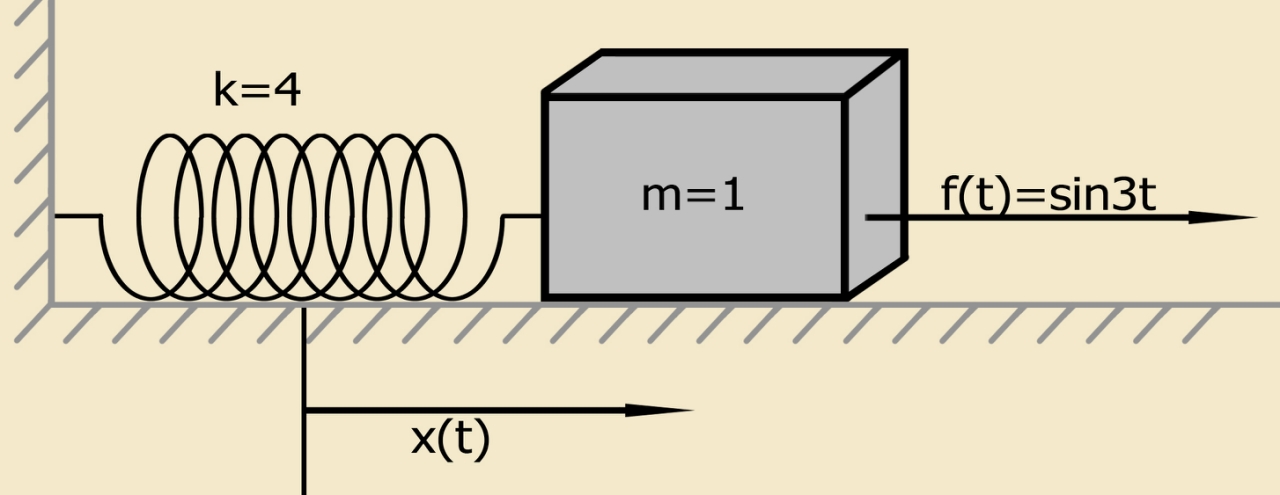
Un système constitué d'un point matériel d'une masse donnée fixé sur un ressort satisfait le problème de Cauchy (problème aux conditions initiales). Le point matériel d'une masse donnée est initialement au repos dans sa position d'équilibre.
Pour résoudre cette équation différentielle linéaire et d'autres par la méthode de transformation de Laplace, il est pratique d'utiliser le système suivant obtenu à partir des relations (3):
L \ left \ {f ^ {IV} (t) \ right \} = s ^ {4} \ cdot F (s) -s ^ {3} \ cdot f (0) -s ^ {2} \ cdot f ^ {I} (0) -s \ cdot f ^ {II} (0) -f ^ {III} (0),L \ left \ {f ^ {III} (t) \ right \} = s ^ {3} \ cdot f (s) -s ^ {2} \ cdot f (0) -s \ cdot f ^ {I } (0) -f ^ {II} (0),L \ left \ {f ^ {II} (t) \ right \} = s ^ {2} \ cdot F (s) -s \ cdot f (0) -f ^ {I} (0),L \ left \ {f ^ {I} (t) \ right \} = s \ cdot F (s) -f (0), L \ left \ {f (t) \ right \} = F (s) .L \ left \ {f (t) \ right \} = F (s). (5)La séquence de solutions utilisant SymPy est la suivante:
- charger les modules nécessaires et définir explicitement les variables symboliques:
from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X', cls=Function)
- spécifier la version de la bibliothèque sympy pour prendre en compte ses fonctionnalités. Pour ce faire, entrez les lignes suivantes:
import SymPy print (' sympy – %' % (sympy._version_))
- selon la signification physique du problème, la variable temporelle est déterminée pour une région comprenant zéro et des nombres positifs. Nous définissons les conditions initiales et la fonction sur le côté droit de l'équation (4) avec sa transformée de Laplace suivante. Pour les conditions initiales, vous devez utiliser la fonction Rational, car l'utilisation de l'arrondi décimal entraîne une erreur.
- en utilisant (5), nous réécrivons les dérivés convertis de Laplace inclus dans le côté gauche de l'équation (4), en formant le côté gauche de cette équation à partir d'eux, et comparons le résultat avec son côté droit:
d2 = s**2*X(s) - s*x0 - x01 d0 = X(s) d = d2 + 4*d0 de = Eq(d, Lg)
- nous résolvons l'équation algébrique obtenue pour la transformation X (s) et effectuons la transformée de Laplace inverse:
rez = solve(de, X(s))[0] soln = inverse_laplace_transform(rez, s, t)
- Nous transférons du travail dans la bibliothèque SymPy vers la bibliothèque NumPy:
f = lambdify(t, soln, 'numpy')
- nous traçons la méthode Python habituelle:
x = np.linspace(0, 6*np.pi, 100) plt.title(', \n :\n (t)=%s' % soln) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2) plt.show()
Texte intégral du programme: from sympy import * import numpy as np import matplotlib.pyplot as plt import sympy var('s') var('t', positive=True) var('X', cls=Function) print (" sympy – %s" % (sympy.__version__))
Nous obtenons:Version de la bibliothèque Sympy - 1.3
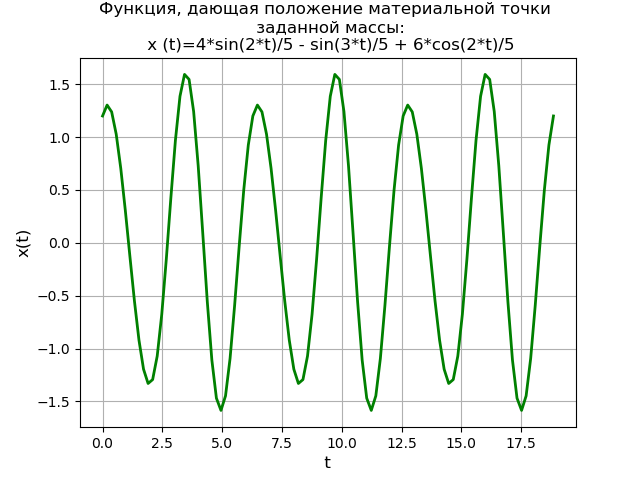
On obtient un graphique de la fonction périodique donnant la position du point matériel d'une masse donnée. La méthode de transformation de Laplace utilisant la bibliothèque SymPy donne une solution non seulement sans la nécessité de trouver d'abord une solution générale à une équation homogène et une solution particulière à l'équation différentielle hétérogène initiale, mais aussi sans avoir besoin d'utiliser la méthode de la fraction élémentaire et les tables de Laplace.
Dans le même temps, la valeur éducative de la méthode des solutions est préservée en raison de la nécessité d'utiliser le système (5) et d'aller à NumPy pour étudier des solutions en utilisant des méthodes plus productives.
Pour démontrer davantage la méthode, nous résolvons le système d'équations différentielles:
begincases2x″+6x−2=0,y″−2x+2y=40 cdot sin(3t), endcases(6)avec conditions initiales
x(0)=y(0)=y′(0)=0.Un modèle physique simplifié défini par le système d'équations (6) dans des conditions initiales nulles:

Ainsi, la force
f (t) est soudainement appliquée au deuxième point matériel d'une masse donnée au temps
t = 0 , lorsque le système est au repos dans sa position d'équilibre.
La solution du système d'équations est identique à la solution précédemment considérée de l'équation différentielle (4), par conséquent, je donne le texte du programme sans explication.
Texte du programme from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t ', positive=True) var('X Y', cls=Function) x0 = 0 x01 = 0 y0 = 0 y01 = 0 g = 40 * sin(3*t) Lg = laplace_transform(g, t, s, noconds=True) de1 = Eq(2*(s**2*X(s) - s*x0 - x01) + 6*X(s) - 2*Y(s)) de2 = Eq(s**2*Y(s) - s*y0 - y01 - 2*X(s) + 2*Y(s) - Lg) rez = solve([de1, de2], X(s), Y(s)) rezX = expand(rez[X(s)]) solnX = inverse_laplace_transform(rezX, s, t) rezY = expand(rez[Y(s)]) solnY = inverse_laplace_transform(rezY, s, t) f = lambdify(t, solnX, "numpy") F = lambdify(t, solnY, "numpy") x = np.linspace(0, 4*np.pi, 100) plt.title(' :\nx(t)=%s\ny(t)=%s' % (solnX, solnY)) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t), y(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2, label='x(t)') plt.plot(x, F(x), 'b', linewidth=2, label='y(t)') plt.legend(loc='best') plt.show()
Nous obtenons: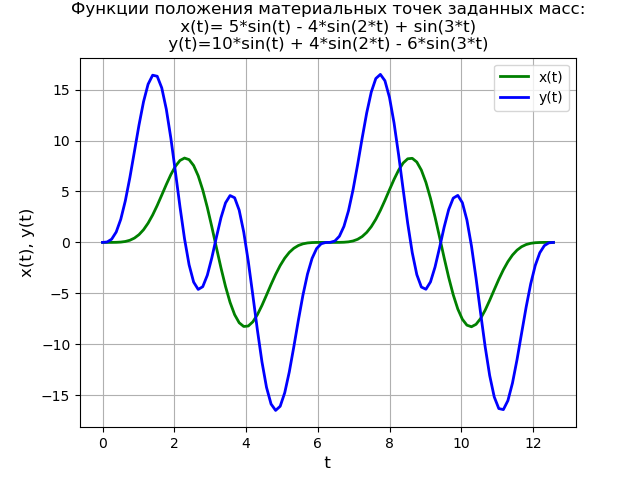
Pour des conditions initiales non nulles, le texte du programme et le graphique de la fonction prendront la forme:
Texte du programme from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X Y', cls=Function) x0 = 0 x01 = -1 y0 = 0 y01 = -1 g = 40 * sin(t) Lg = laplace_transform(g, t, s, noconds=True) de1 = Eq(2*(s**2*X(s) - s*x0 - x01) + 6*X(s) - 2*Y(s)) de2 = Eq(s**2*Y(s) - s*y0 - y01 - 2*X(s) + 2*Y(s) - Lg) rez = solve([de1, de2], X(s), Y(s)) rezX = expand(rez[X(s)]) solnX = (inverse_laplace_transform(rezX, s, t)).evalf().n(3) rezY = expand(rez[Y(s)]) solnY = (inverse_laplace_transform(rezY, s, t)).evalf().n(3) f = lambdify(t, solnX, "numpy") F = lambdify(t, solnY, "numpy") x = np.linspace(0, 4*np.pi, 100) plt.title(' :\nx(t)= %s \ny(t)=%s' % (solnX, solnY)) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t), y(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2, label='x(t)') plt.plot(x, F(x), 'b', linewidth=2, label='y(t)') plt.legend(loc='best') plt.show()
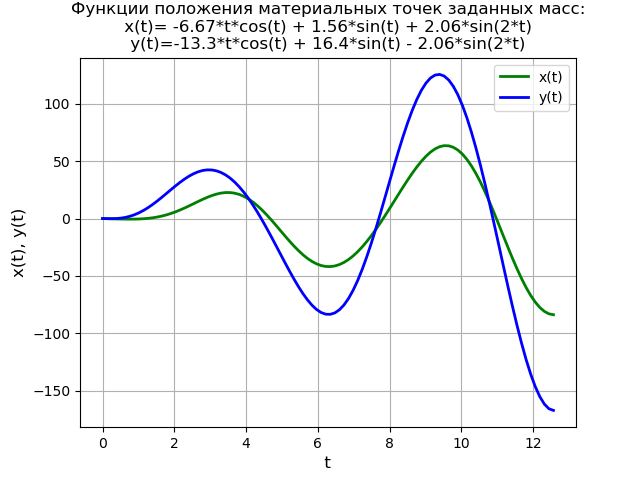
Considérons la solution d'une équation différentielle linéaire du quatrième ordre avec des conditions initiales nulles:
x(4)+2 cdotx″+x=4 cdott cdotet;x(0)=x′(0)=x″(0)=x(3)(0)=0.Texte du programme: from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X', cls=Function)
Calendrier de décision:
Nous résolvons l'équation différentielle linéaire du quatrième ordre:
x(4)+13x″+36x=0;avec conditions initiales
x(0)=x″(0)=0 ,
x′(0)=2 ,
x(3)(0)=−13 .
Texte du programme: from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X', cls=Function)
Calendrier de décision: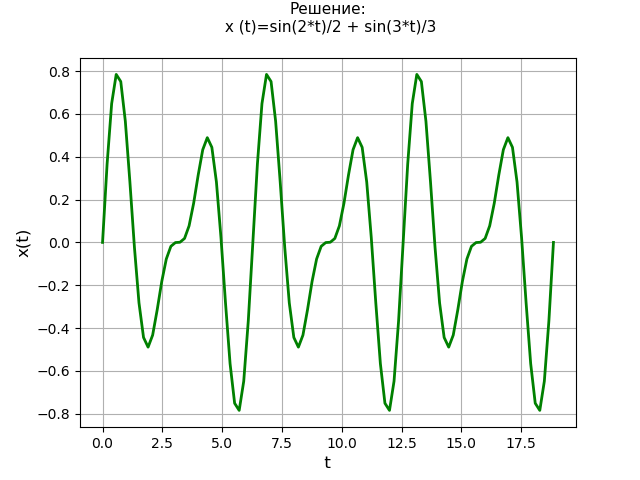
Fonctions pour résoudre ODE
Pour les systèmes ODE et ODE avec une solution analytique, la fonction
dsolve () est utilisée:
sympy.solvers.ode.
dsolve (eq, func = None, hint = 'default', simplify = True, ics = None, xi = None, eta = None, x0 = 0, n = 6, ** kwargs)
Comparons les performances de la fonction dsolve () avec la méthode Laplace. Par exemple, prenez l'équation différentielle du quatrième degré suivante avec des conditions initiales nulles:
x(IV)(t)=3 cdotx‴(t)−x(t)=4 cdott cdot exp(t);x(0)=x′(0)=x″(0)=x‴(0)=0.Un programme utilisant la fonction dsolve (): from sympy import * import time import numpy as np import matplotlib.pyplot as plt start = time.time() var('t C1 C2 C3 C4') u = Function("u")(t)
Nous obtenons:Temps d'équation utilisant la fonction dsolve (): 1,437 s
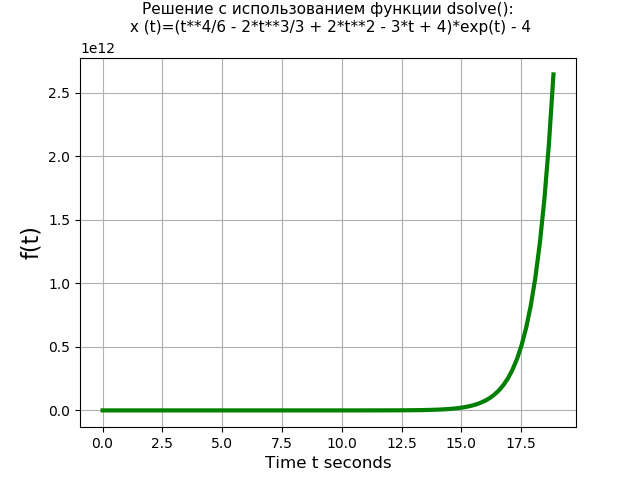
Programme utilisant les transformations de Laplace: from sympy import * import time import numpy as np import matplotlib.pyplot as plt start = time.time() var('s') var('t', positive=True) var('X', cls=Function)
Nous obtenons:Temps d'équation utilisant la transformée de Laplace: 3,274 s

Ainsi, la fonction dsolve () (1,437 s) résout l'équation du quatrième ordre plus rapidement que la résolution par la méthode de transformation de Laplace (3,274 s) plus de deux fois. Cependant, il convient de noter que la fonction dsolve () ne résout pas le système d'équations différentielles de second ordre, par exemple, lors de la résolution du système (6) à l'aide de la fonction dsolve (), une erreur se produit:
from sympy import* t = symbols('t') x, y = symbols('x, y', Function=True) eq = (Eq(Derivative(x(t), t, 2), -3*x(t) + y(t)), Eq(Derivative(y(t), t, 2), 2*x(t) - 2*y(t) + 40*sin(3*t))) rez = dsolve(eq) print (list(rez))
Nous obtenons:raiseNotImplementedError
NotImplementedError
Cette erreur signifie que la solution du système d'équations différentielles utilisant la fonction
dsolve () ne peut pas être représentée symboliquement. Alors qu'avec l'aide des transformées de Laplace, nous avons obtenu une représentation symbolique de la solution, ce qui prouve l'efficacité de la méthode proposée.
RemarqueAfin de trouver la méthode nécessaire pour résoudre des équations différentielles à l'aide de la fonction
dsolve () , vous devez utiliser
classify_ode (eq, f (x)) , par exemple:
from sympy import * from IPython.display import * import matplotlib.pyplot as plt init_printing(use_latex=True) x = Symbol('x') f = Function('f') eq = Eq(f(x).diff(x, x) + f(x), 0) print (dsolve(eq, f(x))) print (classify_ode(eq, f(x))) eq = sin(x)*cos(f(x)) + cos(x)*sin(f(x))*f(x).diff(x) print (classify_ode(eq, f(x))) rez = dsolve(eq, hint='almost_linear_Integral') print (rez)
Nous obtenons:Eq (f (x), C1 * sin (x) + C2 * cos (x))
('nth_linear_constant_coeff_homogeneous', '2nd_power_series_ordinary')
('séparable', '1st_exact', 'presque_linéaire', '1st_power_series', 'lie_group', 'separable_Integral', '1st_exact_Integral', 'presque_linear_Integral')
[Eq (f (x), -acos ((C1 + Integral (0, x)) * exp (-Integral (-tan (x), x))) + 2 * pi), Eq (f (x), acos ((C1 + Integral (0, x)) * exp (-Integral (-tan (x), x)))]]]
Ainsi, pour l'équation
eq = Eq (f (x) .diff (x, x) + f (x), 0) , toute méthode de la première liste fonctionne:
nth_linear_constant_coeff_homogeneous,
2nd_power_series_ordinary
Pour l'équation
eq = sin (x) * cos (f (x)) + cos (x) * sin (f (x)) * f (x) .diff (x) , toute méthode de la deuxième liste fonctionne:
séparable, 1er_exact, presque_linéaire,
1st_power_series, lie_group, separable_Integral,
1st_exact_Integral, presque_linear_Integral
Pour utiliser la méthode sélectionnée, l'entrée de fonction dsolve () prendra la forme, par exemple:
rez = dsolve(eq, hint='almost_linear_Integral')
Conclusion:
Cet article visait à montrer comment utiliser les outils des bibliothèques SciPy et NumPy sur l'exemple de résolution de systèmes ODE linéaires à l'aide de la méthode opérateur. Ainsi, les méthodes de résolution symbolique des équations différentielles linéaires et des systèmes d'équations par la méthode de Laplace ont été considérées. L'analyse des performances de cette méthode et des méthodes implémentées dans la fonction dsolve () est effectuée.
Références:- Équations différentielles et problèmes de valeurs limites: modélisation et calcul à l'aide de Mathematica, Maple et MATLAB. 3e édition.: Per. de l'anglais - M.: LLC «I.D. Williams, 2008. - 1104 p.: Ill. - Paral. tit. Anglais
- Utilisation de la transformée de Laplace inverse pour analyser les liens dynamiques des systèmes de contrôle