Apprenez OpenGL. Leçon 6.1. PBR ou rendu physiquement correct. Théorie

Rendu physiquement correct

PBR, ou rendu physique, est un ensemble de techniques de visualisation basées sur une théorie qui s'accorde assez bien avec la théorie réelle de la propagation de la lumière. Étant donné que le but du PBR est une simulation physiquement fiable de la lumière, il semble beaucoup plus réaliste par rapport aux modèles d'éclairage Phong et Blinn-Fong que nous avons utilisés précédemment. Il a non seulement une meilleure apparence, mais donne également une bonne approximation de la physique réelle, ce qui nous permet (et aux artistes en particulier) de créer des matériaux basés sur les propriétés physiques des surfaces sans recourir à des astuces bon marché afin de rendre l'éclairage réaliste. Le principal avantage de cette approche est que les matériaux que nous créons auront l'aspect prévu quelles que soient les conditions d'éclairage, ce qui ne peut pas être dit à propos d'autres approches, pas PBR.

Cependant, le PBR est toujours une approximation de la réalité (basée sur les lois de la physique), c'est pourquoi il est appelé rendu physiquement correct plutôt que rendu physique. Pour que le modèle d'éclairage puisse être qualifié de physiquement correct, il doit remplir 3 conditions (ne vous inquiétez pas, nous y arriverons bientôt):

• Basé sur un modèle de micro facettes réfléchissantes
• Obéissez à la loi de conservation de l'énergie
• Utiliser la fonction de distribution de réflectance à double faisceau (BRDF)

Dans cette série de didacticiels, nous nous concentrerons sur l'approche PBR, initialement développée chez Disney et adaptée pour une visualisation en temps réel par Epic Games. Leur approche, basée sur un workflow métal-diélectrique (Eng. Metallic workflow, n'a pas pu trouver une meilleure traduction - environ Ed. ), Est bien documentée, largement acceptée dans de nombreux moteurs populaires et a l'air incroyable. À la fin de cette section, nous obtenons quelque chose de similaire à ceci:

Gardez à l'esprit que les articles de cette section sont assez avancés, il est donc recommandé d'avoir une bonne compréhension d'OpenGL et de l'éclairage des shaders. Voici quelques connaissances dont vous aurez besoin pour étudier cette section: tampon d'image , cartes cubiques , correction gamma , HDR et cartes normales . Nous allons aussi approfondir un peu les mathématiques, mais je promets de tout faire pour tout expliquer le plus clairement possible.

Modèle de micro facettes réfléchissantes

Toutes les techniques PBR sont basées sur la théorie des micro faces. Cette théorie dit que chaque surface à fort grossissement peut être représentée comme un ensemble de miroirs microscopiques appelés micro faces . En raison de la rugosité de surface, ces micro-miroirs peuvent être orientés dans différentes directions:

Plus la surface est rugueuse, plus ses micro-faces sont orientées au hasard. Le résultat de cet agencement de ces petits miroirs est (en particulier en ce qui concerne les reflets spéculaires et les réflexions) que les rayons de lumière incidents sont dispersés dans différentes directions sur des surfaces rugueuses, ce qui conduit à une fusée spéculaire plus large. Et vice versa: sur des surfaces lisses, les rayons incidents sont plus susceptibles d'être réfléchis dans une direction, ce qui donnera un éclat plus petit et plus net:

Au niveau microscopique, il n'y a pas de surfaces absolument lisses, mais étant donné que les micro-faces sont suffisamment petites et que nous ne pouvons pas les distinguer dans notre espace de pixels, nous approximons statistiquement la rugosité de la surface en introduisant un coefficient de rugosité . En utilisant ce coefficient, nous pouvons calculer la fraction de micro-faces orientées dans la direction d'un certain vecteur $$$h$ . Ce vecteur $$$h$ rien de plus qu'un vecteur médian situé au milieu entre la direction de la lumière incidente $$$l$ et direction de l'observateur $$$v$ . Nous en avons parlé plus tôt dans une leçon sur l'éclairage avancé , où nous l'avons défini comme le rapport de la somme des vecteurs $$$l$ et $$$v$ à la longueur du vecteur résultant:

$$

$$h = \ frac {l + v} {|| l + v ||}$$

Plus les micro-faces sont orientées dans la direction du vecteur médian, plus le reflet spéculaire sera net et lumineux. Du fait du coefficient de rugosité, qui se situe entre 0 et 1, on peut statistiquement approcher l'orientation des micro faces:

Comme vous pouvez le voir, une valeur plus élevée du coefficient de rugosité donne un spot de reflets miroir de plus grande taille, par rapport à un petit spot pointu sur des surfaces lisses.

Économies d'énergie.

L'utilisation de l'approximation prenant en compte les micro faces comporte déjà une certaine forme de conservation de l'énergie: l'énergie de la lumière réfléchie ne dépassera jamais l'énergie de la lumière incidente (si la surface ne brille pas d'elle-même). En regardant l'image ci-dessus, nous voyons qu'avec une augmentation de la rugosité de surface, le point de lumière réfléchie augmente, mais en même temps sa luminosité diminue. Si l'intensité de la lumière réfléchie était la même pour tous les pixels, quelle que soit la taille du spot, les surfaces plus rugueuses émettraient beaucoup plus d'énergie, ce qui violerait la loi de conservation de l'énergie. Par conséquent, les réflexions spéculaires sont plus lumineuses sur les surfaces lisses et sombres sur les surfaces rugueuses.

Pour conserver l'énergie, nous devons faire une séparation claire entre les composants diffus et miroir. À ce moment, lorsqu'un rayon de lumière atteint la surface, il est divisé en composants réfléchis et réfractés . La composante réfléchie est la lumière réfléchie directement et ne pénètre pas dans la surface; nous la connaissons comme une composante miroir de la lumière. La composante réfractée est la lumière qui pénètre dans la surface et est absorbée par elle - elle nous est connue comme la composante diffuse de la lumière.

Mais il y a quelques nuances associées à l'absorption de la lumière - cela ne se produit pas instantanément, dès que la lumière touche la surface. Du cours de la physique, nous savons que la lumière peut être décrite comme un faisceau de photons dont l'énergie se déplace en ligne droite jusqu'à ce qu'elle perde toute son énergie à la suite d'une collision avec des obstacles. Chaque matériau est constitué de microparticules qui peuvent interagir avec un rayon de lumière, comme le montre la figure ci-dessous. Ces particules absorbent une partie ou la totalité de l'énergie de la lumière à chaque collision, la convertissant en chaleur.

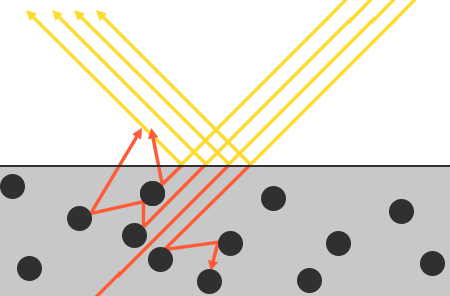
Dans le cas général, toute l'énergie n'est pas absorbée et la lumière continue de se diffuser dans des directions (principalement) aléatoires, où elle entre à nouveau en collision avec d'autres particules jusqu'à ce qu'elle manque d'énergie ou quitte à nouveau la surface. Ainsi, la surface commence à réémettre des rayons lumineux, apportant une contribution sous la forme de la couleur observée (diffuse) de la surface. En utilisant PBR, nous faisons l'hypothèse simplifiée que toute la lumière réfractée est absorbée et diffusée sur une petite zone d'influence, ignorant l'effet de la lumière diffusée qui quitte la surface à une distance de cette zone. Les techniques de shader spéciales qui en tiennent compte, appelées techniques de diffusion souterraine , améliorent considérablement la qualité visuelle des matériaux comme le cuir, le marbre, la cire, mais sont coûteuses en termes de performances.

Des subtilités supplémentaires apparaissent lorsque la lumière est réfractée et réfléchie sur les surfaces métalliques . Les surfaces métalliques interagissent différemment avec la lumière que les surfaces non métalliques (c'est -à- dire les diélectriques). Ils obéissent aux mêmes lois de réfraction et de réflexion, à une exception près: toute la lumière réfractée est absorbée par la surface sans diffusion, il ne reste que la lumière réfléchie par le miroir; en d'autres termes, les surfaces métalliques n'ont pas de couleur diffuse. En raison de cette différence évidente entre les métaux et les diélectriques, ils seront traités différemment dans le convoyeur PBR dans lequel nous irons plus loin au cours de cet article.

Cette différence entre la lumière réfléchie et réfractée nous amène à une autre observation concernant la conservation de l'énergie: leurs valeurs s'excluent mutuellement. L'énergie de la lumière réfléchie ne peut pas être absorbée par le matériau. Par conséquent, l'énergie absorbée par la surface sous forme de lumière réfractée est l'énergie restante après prise en compte de la lumière réfléchie.
Nous utilisons ce rapport, calculant d'abord la partie réfléchie en pourcentage de l'énergie des rayons incidents réfléchis par la surface, puis la fraction de la lumière réfractée directement à partir de la réflexion, comme:

float kS = calculateSpecularComponent(...); // /  float kD = 1.0 - kS; // /  

De cette façon, nous apprenons les significations des parties réfléchies et réfractées grâce à la loi de conservation de l'énergie. Avec cette approche, ni la partie réfractée (diffuse) ni la partie réfléchie ne dépasseront 1,0, garantissant que leur énergie totale ne dépasse pas la valeur de l'énergie lumineuse incidente, ce que nous n'avons pas pu prendre en compte dans les leçons précédentes.

Équation de réflexion

Ce qui précède nous amène à la soi-disant équation de rendu : une équation complexe inventée par des gars très intelligents, et aujourd'hui c'est le meilleur modèle pour simuler l'éclairage. PBR suit strictement une version plus spécifique de cette équation, connue sous le nom d' équation de réflexion . Pour bien comprendre le PBR, il est important d'avoir d'abord une compréhension complète de l'équation de réflexion:

$$

$$L_o (p, \ omega_o) = \ int \ limits_ \ Omega f_r (p, \ omega_i, \ omega_o) L_i (p, \ omega_i) n \ cdot \ omega_id \ omega_i$$

Au début, cela semble effrayant, mais nous le démonterons progressivement, en plusieurs parties, et vous verrez à quel point cela commencera à avoir du sens. Pour comprendre cette équation, il faudra approfondir un peu la radiométrie. La radiométrie est la science de la mesure du rayonnement électromagnétique (y compris la lumière visible). Il existe plusieurs quantités radiométriques que nous pouvons utiliser pour mesurer l'illumination, mais nous n'en utiliserons qu'une seule liée à l'équation de réflexion, connue sous le nom de luminance énergétique (rayonnement anglais) et désignée ici par la lettre L.EI est utilisé pour quantifier la magnitude ou l'intensité de la lumière, venant d'une certaine direction. EJ, à son tour, est une combinaison de plusieurs quantités physiques, et pour qu'il soit plus facile pour nous de l'imaginer, nous nous concentrerons sur chacune d'elles individuellement.

Flux rayonnant

Flux de rayonnement ( $$$\ Phi$ ) est la puissance de l'énergie transmise par la lumière, mesurée en watts. L'énergie totale de la lumière se compose de nombreux termes pour différentes longueurs d'onde, chacun correspondant à sa propre couleur du spectre. L'énergie émise par la source lumineuse, dans ce cas, peut être représentée en fonction de toutes ces longueurs d'onde. Des longueurs d'onde de 390 nm à 700 nm constituent la partie visible du spectre, c'est-à-dire que le rayonnement dans cette plage peut être perçu par l'œil humain. Dans l'image ci-dessous, vous pouvez voir les valeurs des énergies pour différentes longueurs d'onde constituant la lumière du jour:

Le flux de rayonnement correspond à l'aire sous le graphique de cette fonction pour toutes les longueurs d'onde. L'utilisation directe de longueurs d'onde de lumière comme entrée dans l'infographie n'est pas pratique, nous avons donc recours à une représentation simplifiée du flux de rayonnement, au lieu d'utiliser une fonction de toutes les longueurs d'onde, un triplet de couleurs, appelé RVB (ou, comme nous l'appelons habituellement, la couleur de l'éclairage). Une telle vue entraîne une certaine perte d'informations, mais dans l'ensemble, elle affectera légèrement l'image finale.

Angle solide

Angle solide indiqué par $$$\ omega$ nous donne la taille ou l'aire de la figure projetée sur la sphère unitaire. Vous pouvez l'imaginer comme une direction ayant un volume de:

Imaginez que vous êtes au centre d'une sphère et que vous regardez dans la direction de la figure. La taille de la silhouette résultante sera un angle solide.

Intensité de rayonnement

La force de rayonnement mesure la quantité de flux de rayonnement par angle solide ou la force d'une source lumineuse par unité de surface définie par l'angle solide. Par exemple, pour une source de lumière omnidirectionnelle qui émet également dans toutes les directions, la force de rayonnement signifie l'énergie de la lumière par zone spécifique (angle solide):

L'équation décrivant la force du rayonnement ressemble à ceci:

$$

$$I = \ frac {d \ Phi} {d \ omega}$$

, où I est le flux de rayonnement f par angle solide $$${d \ omega}$

Connaissant le flux de rayonnement, la force et l'angle solide, nous pouvons décrire l'équation de luminosité énergétique qui décrit l'énergie totale observée dans la zone A, limitée par l'angle solide O pour la lumière par la force $$$\ Phi$

$$

$$L = \ frac {d ^ 2 \ Phi} {dA d \ omega \ cos \ theta}$$

La luminosité énergétique est la quantité de lumière radiométrique dans une zone qui dépend de l'angle de la lumière incidente. $$$\ theta$ (angle entre la direction de la lumière et la normale à la surface) à travers $$$cos \ theta$ : La lumière est plus faible lorsqu'elle est émise le long de la surface et plus forte lorsqu'elle est perpendiculaire à celle-ci. Ceci est similaire à nos calculs de lumière diffuse dans le didacticiel sur les principes de base de l'éclairage, car $$$cos \ theta$ rien de plus qu'un produit scalaire entre la direction de la lumière et le vecteur normal à la surface:

 float cosTheta = dot(lightDir, N); 

L'équation de luminosité énergétique est très utile pour nous, car elle contient la plupart des quantités physiques qui nous intéressent. Si nous supposons que l'angle solide ω et la zone A sont infinitésimaux, nous pouvons utiliser l'EE pour mesurer le flux d'un rayon de lumière pour un point dans l'espace. Cela nous permettra de calculer l'EI d'un seul rayon lumineux agissant sur un seul point (fragment); nous traduisons en fait l'angle solide $$$\ omega$ dans le vecteur de direction $$$\ omega$ et $$$A$ au point $$$p$ . Ainsi, nous pouvons directement utiliser l'IE dans nos shaders pour calculer la contribution d'un seul rayon lumineux pour chaque fragment.

En fait, en ce qui concerne l'EE, nous sommes généralement intéressés par tous les incidents de lumière entrante sur le point p, qui est la somme de l'EE entière, et est connu sous le nom d'irradiance. Connaissant l'IE et l'irradiation, nous pouvons revenir à l'équation de réflexion:

$$

$$L_o (p, \ omega_o) = \ int \ limits_ \ Omega f_r (p, \ omega_i, \ omega_o) L_i (p, \ omega_i) n \ cdot \ omega_id \ omega_i$$

Nous savons maintenant que $$$L$ dans l'équation de rendu est l'IE pour un point de la surface p et un angle solide infiniment petit de la lumière entrante $$$\ omega_i$ , qui peut être considéré comme un vecteur de direction d'entrée $$$\ omega_i$ . N'oubliez pas que l'énergie est multipliée par $$$cos \ theta$ - l'angle entre la direction d'incidence de la lumière et la normale à la surface, qui est exprimé dans l'équation de réflexion par le produit $$$n \ cdot \ omega_i$ . L'équation de réflexion calcule la somme de l'IE réfléchie $$$L_o (p, \ omega_o)$ des points $$$p$ vers $$$ω_o$ , qui est la direction sortante vers l'observateur. Ou bien: $$$L_o$ mesure l'irradiance réfléchie d'un point $$$p$ si vu de $$$\ omega_o$ .

Étant donné que l'équation de réflexion est basée sur l'irradiation, qui est la somme de tous les rayonnements entrants, nous mesurons la lumière non seulement d'une direction de la lumière entrante, mais de toutes les directions de la lumière entrante dans l'hémisphère $$$\ Omega$ centré à $$$p$ . Il peut être décrit comme une demi-sphère orientée le long de la normale de surface $$$n$ :

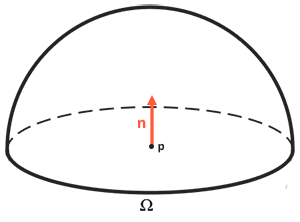
Afin de calculer la somme de toutes les valeurs à l'intérieur de la région, ou, dans le cas d'un hémisphère, le volume, nous intégrons l'équation dans toutes les directions entrantes $$$d \ omega_i$ dans l'hémisphère $$$\ Omega$ . Puisqu'il n'y a pas de solution analytique pour l'équation de rendu et l'équation de réflexion, nous allons résoudre l'intégrale numériquement. Cela signifie que nous obtiendrons des résultats pour de petits pas discrets de l'équation de réflexion de l'hémisphère $$$\ Omega$ et les moyenne sur la taille de l'étape. C'est ce qu'on appelle la somme de Riemann , que nous pouvons représenter grossièrement avec le code suivant:

 int steps = 100; float sum = 0.0f; vec3 P = ...; vec3 Wo = ...; vec3 N = ...; float dW = 1.0f / steps; for(int i = 0; i < steps; ++i) { vec3 Wi = getNextIncomingLightDir(i); sum += Fr(P, Wi, Wo) * L(P, Wi) * dot(N, Wi) * dW; } 

dW pour chaque étape discrète peut être considéré comme $$$d \ omega_i$ dans l'équation de réflexion. Mathématiquement $$$d \ omega_i$ est le différentiel par lequel nous calculons l'intégrale, et bien qu'il ne soit pas identique à dW dans le code (car il s'agit d'une étape discrète de la somme de Riemann), nous pouvons le considérer comme tel pour faciliter le calcul. Gardez à l'esprit que l'utilisation d'étapes discrètes nous donnera toujours une quantité approximative, et non la valeur exacte de l'intégrale. Un lecteur attentif remarquera que nous pouvons augmenter la précision de la somme de Riemann en augmentant le nombre de pas.

L'équation de réflexion résume le rayonnement de toutes les directions de la lumière entrante $$$\ omega_i$ hémisphère $$$\ Omega$ qui atteint le point $$$p$ et renvoie la quantité de lumière réfléchie $$$L_o$ vers le spectateur. Le rayonnement entrant peut provenir de sources lumineuses que nous connaissons déjà ou de cartes environnementales qui déterminent l'IE de chaque direction entrante, dont nous parlerons dans le tutoriel IBL.

Maintenant, la seule inconnue à gauche est le symbole $$$f_r$ , connue sous le nom de fonction BRDF ou fonction de réflectance à deux faisceaux , qui met à l'échelle (ou pèse) la valeur du rayonnement entrant en fonction des propriétés du matériau de surface.

BRDF

BRDF est une fonction qui accepte la direction de la lumière incidente. $$$\ omega_i$ , direction à l'observateur $$$\ omega_o$ normal à la surface $$$n$ et paramètre $$$a$ , qui est la rugosité de surface. BRDF approximativement combien chaque faisceau lumineux individuel $$$\ omega_i$ contribue à la lumière réfléchie finale d'une surface opaque, en tenant compte des propriétés de son matériau. Par exemple, si la surface est complètement lisse (presque comme un miroir), la fonction BRDF renvoie 0,0 pour tous les rayons lumineux entrants $$$\ omega_i$ sauf un ayant le même angle (après réflexion) que le faisceau $$$\ omega_o$ pour lequel la fonction renverra 1.0.

BRDF se rapproche des propriétés réfléchissantes et réfractives d'un matériau sur la base de la théorie des micro-faces mentionnée précédemment. Pour que le BRDF soit physiquement plausible, il doit respecter la loi de conservation de l'énergie, c'est-à-dire que l'énergie totale de la lumière réfléchie ne doit jamais dépasser l'énergie de la lumière incidente. Techniquement, le modèle Blinn-Fong est considéré comme un BRDF acceptant le même $$$\ omega_i$ et $$$\ omega_o$ à l'entrée. Cependant, le modèle Blinn-Fong n'est pas considéré comme physiquement correct, car il ne garantit pas le respect de la loi de conservation de l'énergie. Il existe plusieurs BRDF physiquement corrects pour approximer la réponse de la surface à l'éclairage. Cependant, presque tous les pipelines graphiques en temps réel utilisent le BRDF, connu sous le nom de Cook-Torrance BRDF .

Cook-Torrens BRDF contient à la fois une partie diffuse et une partie miroir:

$$

$$f_r = k_df_ {lambert} + k_sf_ {cuisinier - torrance}$$

ici $$$k_d$ - fraction réfractée d'énergie lumineuse entrante, $$$k_s$ - réfléchi. Le côté gauche du BRDF contient la partie diffuse de l'équation, notée ici comme $$$f_ {lambert}$ . Il s'agit de la diffusion dite de Lambert. Il est similaire à ce que nous avons utilisé pour l'éclairage diffus et est constant:

$$

$$f_ {lambert} = \ frac {c} {\ pi}$$

où $$$c$ - albédo ou couleur de surface (texture de surface diffuse). Division par $$$\ pi$ nécessaire pour normaliser la lumière diffusée, car l'intégrale contenant BRDF indiquée précédemment est multipliée par $$$\ pi$ (nous y reviendrons dans le tutoriel IBL).

Vous serez peut-être surpris de voir à quel point cette diffusion lambertienne ressemble à l'expression d'éclairage diffus que nous avons utilisée auparavant: la couleur de la surface multipliée par le produit scalaire entre la normale de surface et la direction de la lumière. Le produit scalaire est toujours présent, mais déduit de BRDF, puisque nous avons $$$n \ cdot \ omega_i$ dans l'intégrale $$$L_o$ .

Il existe différentes équations pour la partie diffuse de BRDF qui semblent plus réalistes, mais elles sont plus chères en termes de performances. De plus, comme l'ont conclu les Epic Games: la diffusion lambertienne est suffisante pour la plupart des rendus en temps réel.

La partie miroir du Cook-Torrens BRDF est légèrement améliorée et est décrite comme suit:

$$

$$f_ {cook - torrance} = \ frac {DFG} {4 (\ omega_o \ cdot n) (\ omega_i \ cdot n)}$$

Il se compose de trois fonctions et d'un coefficient de normalisation au dénominateur. Chacune des lettres D, F et G représente un certain type de fonction qui se rapproche d'une certaine partie des propriétés réfléchissantes de la surface. Ils sont connus comme la fonction de distribution normale (NDF), l'équation de Fresnel et la fonction Géométrie:

• Fonction de distribution normale: approximation du nombre de microfaces de surface orientées le long du vecteur médian, en fonction de la rugosité de la surface; Il s'agit de la fonction principale d'approximation des micro faces.
• Fonction géométrie: décrit la propriété d'auto-occultation des micro-faces. Lorsque la surface est plutôt rugueuse, certaines micro-faces de la surface peuvent se chevaucher, réduisant ainsi la quantité de lumière réfléchie par la surface.
• Équation de Fresnel: décrit le coefficient de réflexion de surface sous différents angles.

Chacune de ces fonctions est une approximation de leur équivalent physique, et pour elles il existe différentes implémentations visant à une approximation plus précise du modèle physique sous-jacent; certains donnent des résultats plus réalistes, d'autres sont plus efficaces en termes de performances. Brian Caris d'Epic Games a fait de nombreuses recherches sur différents types d'approximations, dont vous pouvez en savoir plus ici . Nous utiliserons les mêmes fonctions que dans Unreal Engine 4 d'Epic Games, à savoir: Trowbridge-Reitz GGX pour D, approximation de Fresnel-Schlick pour F et Schlick-GGX de Smith pour G.

Fonction de distribution normale

La fonction de distribution normale D se rapproche statistiquement de la surface relative des micro faces qui sont précisément orientées le long du vecteur médian $$$h$ . Il existe de nombreux NDF qui déterminent l'approximation statistique de l'alignement global des micro-faces en tenant compte d'un paramètre de rugosité. Nous en utiliserons un connu sous le nom de Trowbridge-Reitz GGX:

$$

$$NDF_ {GGXTR} (n, h, \ alpha) = \ frac {\ alpha ^ 2} {\ pi ((n \ cdot h) ^ 2 (\ alpha ^ 2−1) +1) ^ 2}$$

ici $$$h$ Est le vecteur médian, $$$\ alpha$ - valeur de la rugosité de surface. Si nous choisissons $$$h$ comme vecteur médian entre la normale à la surface et la direction de la lumière, puis en changeant le paramètre de rugosité, nous obtenons l'image suivante:

Lorsque la rugosité est faible (c'est-à-dire que la surface est lisse), les micro faces orientées dans la direction du vecteur médian sont concentrées dans un petit rayon. En raison de cette concentration élevée, le NDF donne un point très lumineux. Sur une surface rugueuse, où les micro-faces sont orientées dans des directions plus aléatoires, vous trouverez un nombre beaucoup plus grand de micro-faces orientées dans la direction du vecteur médian $$$h$ mais situé dans un rayon plus grand, ce qui rend la couleur d'accompagnement plus grise.

Dans le code GLSL, la fonction de distribution normale Trowbridge-Reitz GGX ressemblera à ceci:

 float DistributionGGX(vec3 N, vec3 H, float a) { float a2 = a*a; float NdotH = max(dot(N, H), 0.0); float NdotH2 = NdotH*NdotH; float nom = a2; float denom = (NdotH2 * (a2 - 1.0) + 1.0); denom = PI * denom * denom; return nom / denom; } 

Fonction géométrie

La fonction de géométrie se rapproche statistiquement de la surface relative, où ses irrégularités microscopiques se chevauchent, ce qui empêche les rayons lumineux de pénétrer.

Comme dans le cas du NDF, la fonction de géométrie accepte le coefficient de rugosité de surface en entrée, ce qui dans ce cas signifie ce qui suit: les surfaces plus rugueuses auront une probabilité plus élevée d'ombrage des micro-faces. La fonction de géométrie que nous utiliserons est une combinaison des approximations GGX et Schlick-Beckmann, et est connue sous le nom de Schlick-GGX:

$$

$$G_ {SchlickGGX} (n, v, k) = \ frac {n \ cdot v} {(n \ cdot v) (1 - k) + k}$$

Ici $$$k$ est une nouvelle désignation $$$\ alpha$ selon que l'on utilise la fonction géométrie pour l'éclairage direct ou l'éclairage IBL:

$$

$$k_ {direct} = \ frac {(\ alpha + 1) ^ 2} {8}$$

$$

$$k_ {IBL} = \ frac {\ alpha ^ 2} {2}$$

Veuillez noter que la valeur $$$\ alpha$ peut varier selon la façon dont votre moteur traduit la rugosité en $$$\ alpha$ . Dans les leçons suivantes, nous discuterons en détail comment et où cette réaffectation devient pertinente.

Afin d'approximer efficacement la géométrie, nous devons prendre en compte à la fois la direction de vue (géométrie qui se chevauchent) et le vecteur de direction de la lumière (auto-ombrage de la géométrie). Nous pouvons considérer les deux cas en utilisant la méthode Smith :

$$

$$G (n, v, l, k) = G_ {sub} (n, v, k) G_ {sub} (n, l, k)$$

Utilisation de la méthode Smith avec Schlick-GGX comme $$$G_ {sub}$ donne l'image suivante avec différentes rugosités R:

La fonction de géométrie est un facteur compris entre [0,0, 1,0], où le blanc (ou 1,0) signifie aucun ombrage des micro-faces et le noir (ou 0,0) signifie l'ombrage complet des micro-faces.

Dans GLSL, une fonction de géométrie est convertie en le code suivant:

 float GeometrySchlickGGX(float NdotV, float k) { float nom = NdotV; float denom = NdotV * (1.0 - k) + k; return nom / denom; } float GeometrySmith(vec3 N, vec3 V, vec3 L, float k) { float NdotV = max(dot(N, V), 0.0); float NdotL = max(dot(N, L), 0.0); float ggx1 = GeometrySchlickGGX(NdotV, k); float ggx2 = GeometrySchlickGGX(NdotL, k); return ggx1 * ggx2; } 

Équation de Fresnel

L'équation de Fresnel décrit le rapport de la lumière réfléchie et réfractée, qui dépend de l'angle sous lequel nous regardons la surface. Lorsque la lumière frappe une surface, l'équation de Fresnel nous donne le pourcentage de lumière réfléchie en fonction de l'angle sous lequel nous voyons cette surface. A partir de ce rapport de réflexion et de la loi de conservation de l'énergie, on peut directement obtenir la partie réfractée de la lumière, qui sera égale à l'énergie restante.

Chaque surface ou matériau a un niveau de réflectivité de base , observé en regardant directement la surface, mais si vous regardez la surface sous un angle, toutes les réflexions deviennent plus visibles. Vous pouvez le vérifier vous-même en regardant votre table probablement en bois ou en métal d'abord perpendiculairement puis à un angle proche de 90 degrés. Vous verrez que les reflets deviennent beaucoup plus visibles. Toutes les surfaces, théoriquement, réfléchissent pleinement la lumière lorsqu'elles sont vues à partir d'elles à un angle idéal de 90 degrés. Cet effet est appelé Fresnel et est décrit par l'équation de Fresnel .

L'équation de Fresnel est assez complexe, mais, heureusement, elle peut être simplifiée en utilisant l'approximation de Fresnel-Schlick :

$$

$$F_ {Schlick} (h, v, F_0) = F_0 + (1 - F_0) (1− (h \ cdot v)) ^ 5$$

$$$F_0$ représente la réflectivité de base de la surface, que nous calculons en utilisant quelque chose appelé indices de réfraction ou IOR (indices de réfraction) et, comme vous pouvez le voir sur la surface de la sphère, plus la direction d'observation est proche des limites de la sphère visible (l'angle entre la direction d'observation et la médiane 90 ), , , :

, . , - . (), , . , ( $$$F_0$ ) ( 0 , ) -, , .

. , , :

: 0.17, , , ( ) 0.5 1.0. , “”, $$$F_0$ RGB ( ).

, metallic workflow: , (metalness), , .

: , ; , . , 0.0 1.0. - , , , . , .

$$$F_0$ , , - , , . :

 vec3 F0 = vec3(0.04); F0 = mix(F0, surfaceColor.rgb, metalness); 

, . , $$$F_0$ . 0.04 . , , , F0 . , , .

- :

 vec3 fresnelSchlick(float cosTheta, vec3 F0) { return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0); } 

cosTheta .

-

BRDF - :

$$

$$L_o(p,\omega_o)=\int\limits_\Omega(k_d\frac{c}{\pi}+k_s\frac{DFG}{4(\omega_o\cdot n)(\omega_i \cdot n)}) L_i(p, \omega_i)n\cdot \omega_i d\omega_i$$

. , , F . $$$k_s$ , , $$$k_s$ . , :

$$

$$L_o(p,\omega_o)=\int\limits_\Omega(k_d\frac{c}{\pi}+\frac{DFG}{4(\omega_o\cdot n)(\omega_i \cdot n)}) L_i(p, \omega_i)n\cdot \omega_i d\omega_i$$

, PBR. , , . , , .

PBR

, PBR, , , PBR. , PBR, . , : , .

, PBR, :

: , . , . , ; .

: , , . , , .

: . , PBR-, , : .

: , . . , . PBR- , , (1.0 — ) .

AO (ambient occlusion) : AO . , , . AO , . . , 3D-.

. PBR, , . , PBR, PBR-, , , .

• Background: Physics and Math of Shading by Naty Hoffmann: , , ; PBR, must-read .
• Real shading in Unreal Engine 4 : PBR, Epic Games Unreal Engine 4. PBR, , .
• Marmoset: PBR Theory : PBR. , , , .
• Coding Labs: Physically based rendering : , PBR.
• Coding Labs: Physically Based Rendering — Cook–Torrance : BRDF -
• Wolfire Games — Physically based rendering : PBR Lukas Orsvärn.
• [SH17C] Physically Based Shading : shadertoy (: ) Krzysztof Narkowi, PBR.