Le principe de moindre action. 2e partie

La dernière fois, nous avons brièvement examiné l'un des principes physiques les plus remarquables - le principe de la moindre action, et nous sommes arrêtés sur un exemple qui, semble-t-il, le contredit. Dans cet article, nous traiterons de ce principe plus en détail et verrons ce qui se passe dans cet exemple.

Cette fois, nous avons besoin d'un peu plus de mathématiques. Cependant, je vais essayer de reprendre la partie principale de l'article à un niveau élémentaire. Je vais souligner des points un peu plus rigoureux et complexes, ils peuvent être sautés sans préjudice de la compréhension de base de l'article.

Conditions aux limites

Nous commencerons par l'objet le plus simple - une balle se déplaçant librement dans l'espace, sur laquelle aucune force n'agit. Une telle balle, comme on le sait, se déplace de manière uniforme et rectiligne. Pour simplifier, supposons qu'il se déplace le long de l'axe $$$x$ :

Pour décrire avec précision son mouvement, en règle générale, les conditions initiales sont spécifiées. Par exemple, il est spécifié qu'au moment initial du temps $$$t_A$ la balle était à un point $$$A$ avec coordonnée $$$x_A$ et avait de la vitesse $$$v_A$ . Après avoir défini les conditions initiales sous cette forme, nous déterminons uniquement le mouvement ultérieur de la balle - elle se déplacera à une vitesse constante et sa position au moment $$$t$ sera égal à la position initiale plus la vitesse multipliée par le temps écoulé: $$$x (t) = x_A + v_A \ cdot (t-t_A)$ . Cette façon de fixer les conditions initiales est très naturelle et intuitivement familière. Nous avons demandé toutes les informations nécessaires sur le mouvement de la balle au moment initial, puis son mouvement est déterminé par les lois de Newton.

Cependant, ce n'est pas le seul moyen de spécifier le mouvement de la balle. Une autre alternative consiste à définir la position de la balle à deux moments différents. $$$t_A$ et $$$t_B$ . C'est-à-dire demander que:

1) au moment $$$t_A$ la balle était à un point $$$A$ (avec coordonnée $$$x_A$ );
2) au moment $$$t_B$ la balle était à un point $$$B$ (avec coordonnée $$$x_B$ )

L'expression "était à un point $$$A$ "Cela ne signifie pas que la balle reposait à un point $$$A$ . À l'heure $$$t_A$ il pourrait survoler un point $$$A$ . Cela signifie que sa position au moment $$$t_A$ coïncidé avec un point $$$A$ . La même chose s'applique au point $$$B$ .

Ces deux conditions déterminent également de manière unique le mouvement de la balle. Son mouvement est facile à calculer. Pour satisfaire les deux conditions, la vitesse du ballon doit évidemment être $$$(x_B-x_A) / (t_B-t_A)$ . Position de la balle au moment $$$t$ sera à nouveau égal à la position initiale plus la vitesse multipliée par le temps écoulé:

$$ $$x (t) = x_A + ((x_B-x_A) / (t_B-t_A)) \ cdot (t-t_A)$$

Notez que dans les conditions du problème, nous n'avions pas besoin de régler la vitesse initiale. Elle est uniquement déterminée à partir des conditions 1) et 2).

Le réglage des conditions de la deuxième manière semble inhabituel. Il n'est peut-être pas clair pourquoi, en général, il peut être nécessaire de les poser sous cette forme. Cependant, dans le principe de moindre action, ce sont précisément les conditions sous la forme 1) et 2) qui sont utilisées, et non sous forme de réglage de la position initiale et de la vitesse initiale.

Trajectoire de moindre action

Écartons maintenant un peu du véritable mouvement libre de la balle et considérons le problème purement mathématique suivant. Supposons que nous ayons une balle que nous pouvons déplacer manuellement comme bon nous semble. Dans ce cas, nous devons remplir les conditions 1) et 2). C'est-à-dire entre les deux $$$t_A$ et $$$t_B$ nous devons le déplacer du point $$$A$ au point $$$B$ . Cela peut être fait de différentes manières. Chacune de ces méthodes sera appelée la trajectoire de la balle et elle peut être décrite par la fonction de la position de la balle dans le temps $$$x (t)$ . Reportons plusieurs de ces trajectoires sur le graphique de la dépendance de la position de la balle dans le temps:

Par exemple, nous pouvons déplacer la balle à la même vitesse égale à $$$(x_B-x_A) / (t_B-t_A)$ (chemin vert). Ou nous pouvons le garder à mi-chemin $$$A$ puis doublez la vitesse pour passer au point $$$B$ (trajectoire bleue). Vous pouvez d'abord le déplacer dans la direction opposée. $$$B$ côté et puis déjà passer à $$$B$ (trajectoire brune). Vous pouvez le déplacer d'avant en arrière (trajectoire rouge). En général, vous pouvez le déplacer comme vous le souhaitez, si seules les conditions 1) et 2) sont respectées.

Pour chacune de ces trajectoires, nous pouvons faire correspondre un nombre. Dans notre exemple, c'est-à-dire en l'absence de forces agissant sur la balle, ce nombre est égal à l'énergie cinétique totale accumulée pendant toute la durée de son mouvement dans l'intervalle entre $$$t_A$ et $$$t_B$ et est appelé une action.

Dans ce cas, le mot énergie cinétique "accumulée" ne transmet pas exactement le sens. En réalité, l'énergie cinétique ne s'accumule nulle part; l'accumulation n'est utilisée que pour calculer l'action de la trajectoire. En mathématiques, pour une telle accumulation, il existe un très bon concept - l'intégrale:

$$ $$S = \ int \ limits_ {t_A} ^ {t_B} Tdt$$

L'action est généralement indiquée par la lettre $$$S$ . Symbole $$$T$ signifie énergie cinétique. Cette intégrale signifie que l'action est égale à l'énergie cinétique accumulée de la balle sur une période de temps $$$t_A$ avant $$$t_B$ .

Par exemple, prenons une balle pesant 1 kg., Définissons des conditions aux limites et calculons l'action pour deux trajectoires différentes. Laissez le point $$$B$ est à 1 mètre du point $$$A$ et le temps $$$t_B$ loin du temps $$$t_A$ pendant 1 seconde. C'est-à-dire nous devons déplacer la balle qui au moment initial était au point $$$A$ , en une seconde à une distance de 1 m le long de l'axe $$$x$ .

Dans le premier exemple (trajectoire verte), nous avons déplacé la balle uniformément, c'est-à-dire avec la même vitesse, qui doit évidemment être égale à: $$$v = 1$ m / s L'énergie cinétique de la balle à chaque instant est égale à: $$$T = mv ^ 2/2$ = 1/2 J. En une seconde, 1/2 J s'accumulera $$$\ cdot$ avec énergie cinétique. C'est-à-dire valable pour une telle trajectoire est: $$$S = 1/2$ J $$$\ cdot$ s

Maintenant, ne transférons pas immédiatement la balle du point $$$A$ au point $$$À$ et maintenez-le à un point pendant une demi-seconde $$$A$ , puis, pour le temps restant, nous le transférons uniformément au point $$$B$ . Dans la première demi-seconde, la balle est au repos et son énergie cinétique est nulle. Par conséquent, la contribution à l'action de cette partie de la trajectoire est également égale à zéro. Pendant la seconde demi-seconde, nous transférons le ballon à double vitesse: $$$v = 2$ m / s L'énergie cinétique sera égale à $$$T = mv ^ 2/2$ = 2 J.La contribution de cette période à l'action sera de 2 J multipliée par une demi-seconde, soit 1 J $$$\ cdot$ s Par conséquent, l'action générale pour une telle trajectoire est égale à $$$S = 1$ J $$$\ cdot$ s

De même, toute autre trajectoire avec les conditions aux limites spécifiées 1) et 2) correspond à un certain nombre égal à l'action pour une trajectoire donnée. Parmi toutes ces trajectoires, il existe une trajectoire dans laquelle l'action est la moins importante. On peut prouver que cette trajectoire est une trajectoire verte, c'est-à-dire mouvement uniforme du ballon. Pour toute autre trajectoire, aussi délicate soit-elle, l'action sera supérieure à 1/2.

En mathématiques, une telle comparaison pour chaque fonction d'un certain nombre est appelée fonctionnelle. Assez souvent en physique et en mathématiques, des tâches comme la nôtre se posent, c'est-à-dire pour trouver une fonction pour laquelle la valeur d'une fonction particulière est minimale. Par exemple, l'une des tâches de grande importance historique pour le développement des mathématiques est le problème de la bachistochrone . C'est-à-dire trouver une courbe le long de laquelle la balle roule le plus rapidement. Encore une fois, chaque courbe peut être représentée par la fonction h (x), et chaque fonction peut se voir attribuer un numéro, dans ce cas le temps de roulement de la balle. Encore une fois, le problème se résume à trouver une fonction pour laquelle la valeur de la fonction est minimale. Le domaine des mathématiques qui traite de tels problèmes est appelé le calcul des variations.

Principe de moindre action

Dans les exemples discutés ci-dessus, nous avons deux trajectoires spéciales obtenues de deux manières différentes.

La première trajectoire est obtenue à partir des lois de la physique et correspond à la trajectoire réelle d'une balle libre, qui n'est affectée par aucune force et pour laquelle les conditions aux limites sont données sous la forme 1) et 2).

La deuxième trajectoire est obtenue à partir du problème mathématique de trouver une trajectoire avec des conditions aux limites données 1) et 2), pour lesquelles l'action est minimale.

Le principe de moindre action stipule que ces deux trajectoires doivent coïncider. En d'autres termes, si l'on sait que la balle s'est déplacée de telle manière que les conditions aux limites 1) et 2) ont été satisfaites, alors elle s'est nécessairement déplacée le long d'un chemin pour lequel l'action est minimale par rapport à tout autre chemin avec les mêmes conditions aux limites.

On pourrait considérer cela comme une simple coïncidence. Il existe de nombreux problèmes dans lesquels des trajectoires uniformes et des lignes droites apparaissent. Cependant, le principe de moindre action est un principe très général, valable dans d'autres situations, par exemple pour le mouvement de la balle dans un champ gravitationnel uniforme. Pour ce faire, il vous suffit de remplacer l'énergie cinétique par la différence d'énergie cinétique et potentielle. Cette différence est appelée la fonction Lagrangienne ou Lagrange et l'action devient maintenant égale au total Lagrangien accumulé. En fait, la fonction Lagrange contient toutes les informations nécessaires sur les propriétés dynamiques du système.

Si nous lançons une balle dans un champ de gravité uniforme afin qu'elle passe un point $$$A$ au moment $$$t_A$ et a volé au point $$$B$ au moment $$$t_B$ puis, selon les lois de Newton, il pilotera une parabole. C'est cette parabole qui coïncide avec les trajectoires pour lesquelles l'action sera minimale.

Ainsi, pour un corps se déplaçant dans un champ potentiel, par exemple dans le champ gravitationnel de la Terre, la fonction de Lagrange est égale à: $$$L = T (v) -V (x, y, z)$ . Énergie cinétique $$$T$ dépend de la vitesse du corps et du potentiel - de sa position, c.-à-d. coordonnées $$$x, y, z$ . En mécanique analytique, l'ensemble des coordonnées déterminant la position d'un système est généralement désigné par une lettre $$$q$ . Pour une balle se déplaçant librement dans un champ gravitationnel, $$$q$ signifie coordonnées $$$x$ , $$$y$ et $$$z$ .

Pour indiquer le taux de variation d'une quantité, en physique, très souvent, ils mettent simplement fin à cette quantité. Par exemple $$$\ dot x$ indique le taux de changement de coordonnées $$$x$ , ou, en d'autres termes, la vitesse du corps dans la direction $$$x$ . En utilisant ces conventions, la vitesse de notre balle en mécanique analytique est notée comme $$$\ dot q$ . C'est-à-dire $$$\ dot q$ composants de vitesse moyenne $$$v_x, v_y, v_z$ .

Étant donné que la fonction Lagrange dépend de la vitesse et des coordonnées, elle peut également dépendre explicitement du temps (dépend explicitement du temps signifie que la valeur $$$L$ à différents moments, différents, aux mêmes vitesses et positions du ballon), l'action sous forme générale s'écrit:

$$ $$S = \ int \ limits_ {t_A} ^ {t_B} L (\ dot q, q, t) dt$$

Pas toujours minimal

Cependant, à la fin de la partie précédente, nous avons examiné un exemple où le principe de moindre action ne fonctionne clairement pas. Pour ce faire, nous avons de nouveau pris une balle libre, qui n'est affectée par aucune force, et avons placé une paroi de ressort à côté d'elle.
Nous définissons les conditions aux limites de telle sorte que les points $$$A$ et $$$B$ correspondre. C'est-à-dire et au moment $$$t_A$ et au moment $$$t_B$ la balle doit être au même point $$$A$ . L'une des trajectoires possibles sera la position du ballon en place. C'est-à-dire tout le temps entre $$$t_A$ et $$$t_B$ il se tiendra à un point $$$A$ . L'énergie cinétique et potentielle dans ce cas sera égale à zéro, donc l'action pour une telle trajectoire sera également égale à zéro.

À strictement parler, l'énergie potentielle peut être prise non pas égale à zéro, mais à n'importe quel nombre, car la différence d'énergie potentielle à différents points de l'espace est importante. Cependant, un changement dans la valeur de l'énergie potentielle n'affecte pas la recherche d'une trajectoire avec une action minimale. C'est juste que pour toutes les trajectoires, la valeur de l'action changera du même nombre, et la trajectoire avec une action minimale restera la trajectoire avec une action minimale. Pour plus de commodité, pour notre balle, nous choisirons l'énergie potentielle égale à zéro.

Une autre trajectoire physique possible avec les mêmes conditions aux limites serait une trajectoire dans laquelle le ballon vole d'abord vers la droite, passant un point $$$A$ au moment $$$t_A$ . Puis il entre en collision avec le ressort, le comprime, le ressort, se redressant, repousse la balle, et encore il vole au-delà de la pointe $$$A$ . Vous pouvez choisir la vitesse de la balle pour qu'elle rebondisse sur le mur et vole un point $$$A$ en ce moment $$$t_B$ . L'action avec cette trajectoire sera fondamentalement égale à l'énergie cinétique accumulée pendant le vol entre le point $$$A$ et le mur et le dos. Il y aura une certaine période de temps où la balle comprime le ressort et son énergie potentielle augmente, et pendant cette période, l'énergie potentielle apportera une contribution négative à l'action. Mais une telle période de temps ne sera pas très longue et l'action ne se réduira pas considérablement.



La figure montre les deux trajectoires physiquement possibles du ballon. Le chemin vert correspond à une balle au repos, tandis que le bleu correspond à une balle rebondissant sur la paroi du ressort.

Cependant, un seul d'entre eux a un effet minimal, à savoir le premier! La deuxième trajectoire a plus d'action. Il s'avère que dans ce problème il y a deux trajectoires physiquement possibles et une seule avec une action minimale. C'est-à-dire dans ce cas, le principe de moindre action ne fonctionne pas.

Points stationnaires

Pour comprendre quel est le problème ici, s'écartons du principe de moindre action pour l'instant et reprenons les fonctions habituelles. Prenons une fonction $$$y (x)$ et dessiner son horaire:

Sur le graphique, j'ai marqué quatre points spéciaux en vert. Qu'est-ce qui est commun à ces points? Imaginez qu'un graphe de fonction est une véritable diapositive sur laquelle une balle peut rouler. Les quatre points marqués sont spéciaux en ce que si vous installez la balle exactement à ce point, elle ne roulera nulle part. À tous les autres points, par exemple le point E, il ne pourra pas rester en place et commencera à glisser vers le bas. Ces points sont appelés stationnaires. Trouver de tels points est une tâche utile, car tout maximum ou minimum de la fonction, si elle n'a pas de nœuds nets, doit être un point stationnaire.

Si nous classons plus précisément ces points, alors le point A est le minimum absolu de la fonction, c'est-à-dire sa valeur est inférieure à toute autre valeur de fonction. Le point B - n'est ni un maximum ni un minimum et est appelé un point de selle. Le point C est appelé un maximum local, c'est-à-dire sa valeur est supérieure à celle des points voisins de la fonction. Et le point D est un minimum local, c'est-à-dire sa valeur est inférieure à celle des points voisins de la fonction.

La recherche de tels points est effectuée par une branche des mathématiques appelée analyse mathématique. D'une autre manière, elle est parfois appelée analyse de l'infinitésimal, car elle sait travailler avec des quantités infinitésimales. Du point de vue de l'analyse mathématique, les points stationnaires ont une propriété particulière, grâce à laquelle ils se trouvent. Pour comprendre ce qu'est cette propriété, nous devons comprendre à quoi ressemble la fonction à de très petites distances de ces points. Pour ce faire, nous prenons un microscope et le regardons sur nos points. La figure montre à quoi ressemble la fonction au voisinage de divers points à différents grossissements.

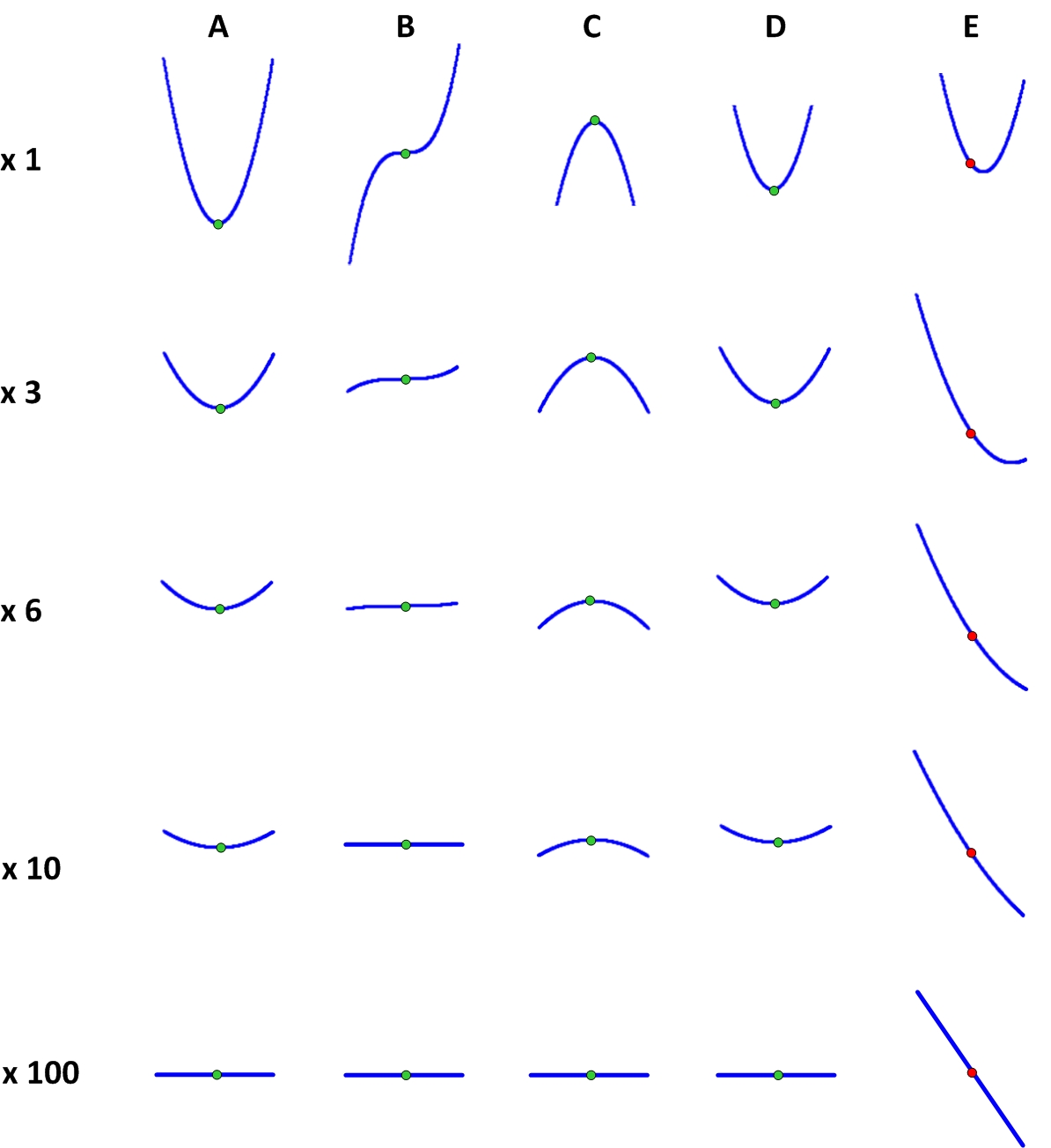
On peut voir qu'à un très grand grossissement (c'est-à-dire à de très petits écarts x), les points stationnaires ont exactement la même apparence et diffèrent considérablement du point non stationnaire. Il est facile de comprendre quelle est cette différence: le graphique de la fonction à un point stationnaire avec l'augmentation devient une ligne strictement horizontale, et dans un point non stationnaire, il devient une ligne inclinée. C'est pourquoi une balle montée à un point fixe ne roulera pas.

L'horizontalité de la fonction au point stationnaire peut s'exprimer différemment: la fonction au point stationnaire ne change pratiquement pas avec un très petit changement dans son argument $$$x$ , même par rapport à l'argument lui-même. La fonction est à un point non stationnaire avec un petit changement $$$x$ varie en proportion de $$$x$ . Et plus l'angle de la fonction est grand, plus la fonction change lors du changement $$$x$ . En effet, la fonction de taille croissante devient de plus en plus similaire à la tangente au graphe au point considéré.

Dans un langage mathématique strict, l'expression «fonction ne change pratiquement pas à un point $$$x_0$ avec très peu de changement $$$x$ "Signifie que le rapport du changement de fonction et le changement de son argument $$$Δy / Δx$ tend à 0 à $$$∆x$ tendant vers 0:

$$$$ affiche $$ \ lim_ {Δx \ à 0} \ frac {Δy (x_0)} {Δx} = \ lim_ {x \ à 0} \ frac {y (x_0 + Δx) -y (x_0) } {∆x} = 0 $$ afficher $$

Pour un point non stationnaire, ce rapport tend vers un nombre différent de zéro, qui est égal à la pente de la fonction à ce point. Le même nombre est appelé la dérivée de la fonction à un point donné. La dérivée de la fonction montre à quelle vitesse la fonction change près d'un point donné avec un petit changement dans son argument $$$x$ . Ainsi, les points stationnaires sont des points où la dérivée de la fonction est 0.

Trajectoires stationnaires

Par analogie avec les points stationnaires, le concept de trajectoires stationnaires peut être introduit. Rappelons que chaque trajectoire correspond à une certaine valeur d'action, c'est-à-dire un certain nombre. Il peut alors y avoir une trajectoire telle que pour des trajectoires proches des mêmes conditions aux limites, les valeurs d'action correspondantes ne diffèrent pratiquement pas de l'action pour la trajectoire stationnaire elle-même. Une telle trajectoire est dite stationnaire. En d'autres termes, toute trajectoire proche du stationnaire aura une valeur d'action qui diffère très peu de l'action pour cette trajectoire stationnaire.

Encore une fois, dans le langage mathématique "peu différent" a la signification exacte suivante. Disons que nous avons un fonctionnel $$$S (x (t))$ pour les fonctions avec les conditions aux limites requises 1) et 2), c'est-à-dire $$$x (t_A) = A$ et $$$x (t_B) = B$ . Supposons que la trajectoire $$$x (t)$ - stationnaire.

Nous pouvons prendre toute autre fonction. $$$g (t)$ de telle sorte qu'à la fin, il prend des valeurs nulles, c'est-à-dire $$$g (t_A)$ = $$$g (t_B)$ = 0. Prenez également la variable $$$ε$ que nous ferons de moins en moins. De ces deux fonctions et variable $$$ε$ on peut faire une troisième fonction $$$x '(t) = x (t) + εg (t)$ , $$$f'(t_A)=A$ $$$f'(t_B)=B$ . $$$ε$ , $$$x'(t)$ , $$$x(t)$ .

$$$ε$ $$$x'(t)$ $$$x(t)$ $$$ε$ . C'est-à-dire

$$limε→0S(x′(t))−S(x(t))ε=limε→0S(x(t)+εg(t))−S(x(t))ε=0 $$\lim_{ε \to 0} \frac {S(x'(t))-S(x(t))}ε=\lim_{ε \to 0} \frac {S(x(t)+εg(t))-S(x(t))}ε = 0$$

$$$g(t)$ , $$$g(t_A)$ = $$$g(t_B)$ = 0.

(, , ) $$$δS$ . «» « ».

$$$δS=0$ .

La méthode de recherche des fonctions stationnaires (non seulement pour le principe de moindre action, mais aussi pour de nombreux autres problèmes) a été trouvée par deux mathématiciens - Euler et Lagrange. Il s'avère que la fonction stationnaire, dont la fonction est exprimée par une intégrale similaire à l'intégrale d'action, doit satisfaire une certaine équation, qui est maintenant appelée l'équation d'Euler-Lagrange.

Principe stationnaire

La situation avec un minimum d'action pour les trajectoires est similaire à la situation avec un minimum pour les fonctions. Pour que la trajectoire ait le moins d'effet, elle doit être une trajectoire stationnaire. Cependant, toutes les trajectoires stationnaires ne sont pas des trajectoires avec une action minimale. Par exemple, une trajectoire stationnaire peut avoir localement une action minimale. C'est-à-direson action sera inférieure à celle de toute autre trajectoire adjacente. Cependant, quelque part loin, il peut y avoir d'autres trajectoires pour lesquelles l'action sera encore moins.

Il s'avère que les corps réels ne se déplacent pas nécessairement le long de trajectoires avec le moins d'action. Ils peuvent se déplacer le long d'un ensemble plus large de trajectoires spéciales, à savoir les trajectoires stationnaires. C'est-à-direla trajectoire réelle du corps sera toujours stationnaire. Par conséquent, le principe de moindre action est plus correctement appelé principe d'action stationnaire. Cependant, selon la tradition établie, il est souvent appelé le principe de moindre action, impliquant pour cela non seulement la minimalité, mais aussi la stationnarité des trajectoires.

Maintenant, nous pouvons écrire le principe de l'action stationnaire dans un langage mathématique, comme il est généralement écrit dans les manuels:

$$ $$δS=δ\int\limits_{t_A}^{t_B} L(\dot q,q,t)dt = 0$$

.

Ici $$$q$Sont des coordonnées généralisées, c'est-à-dire un ensemble de variables qui spécifient uniquement la position du système.
$$$\dot q$ - le taux de variation des coordonnées généralisées.
$$$L(\dot q,q,t)$ - la fonction de Lagrange, qui dépend des coordonnées généralisées, de leurs vitesses et, éventuellement, du temps.
$$$S$ - une action qui dépend de la trajectoire spécifique du système (i.e. $$$q(t)$ )

Les trajectoires réelles du système sont stationnaires, c'est-à-dire pour eux une variation d'action$$$δS=0$ .

Si nous revenons à l'exemple avec une balle et une paroi élastique, alors l'explication de cette situation devient maintenant très simple. Étant donné les conditions aux limites que la balle devrait également$$$t_A$ et pendant $$$t_B$ aller droit au but $$$A$ . . , . , , . .

( ) , .