
Vous avez probablement une question raisonnable: pourquoi?
D'un point de vue pragmatique, il n'y a pas besoin) Vous pouvez toujours utiliser du Tungsten conditionnel, et si vous avez besoin de le faire en python, alors utilisez des modules spéciaux qui ne sont pas si difficiles à maîtriser.
Mais si on vous a soudainement confié une telle tâche ou si vous aimez vraiment la programmation, comme moi, vous aurez des heures passionnantes - et parfois pas très - d'écriture d'un programme et de débogage)
Lors de l'écriture de ce chef-d'œuvre, nous avons vraiment besoin d'un débogage étape par étape, veuillez donc télécharger PyCharm, VS ou autre chose avec cette fonctionnalité. Pour construire des tables, l'absence de cette fonction n'est pas si critique, mais pour tracer ...
Alors, quel sera mon programme. En entrée, il prendra trois valeurs: le début et la fin du segment sur lequel nous voulons voir notre fonction et le pas avec lequel nous allons nous déplacer. Ensuite, nous allons dessiner un tableau de valeurs de fonction à chaque point de la plage de valeurs spécifiées par les données d'entrée. Eh bien, nous allons ensuite dessiner le graphique de la fonction elle-même avec l'axe y mobile.
Alors allons-yPour commencer, je déclarerai plusieurs fonctions dont nous considérerons les valeurs. Je vais surtout prendre assez simple
from math import sqrt def y1(x): return x**3 - 2*x**2 + 4*x - 8 def y2(x): return 1 - 1/x**2 def y3(x): return sqrt(abs(y1(x)*y2(x)))
Nous avons maintenant trois fonctions, dont deux ont un point d'arrêt. À partir du module mathématique, qui stocke tous les petits pains mathématiques (y compris les cosinus, les arctangentes et autres trigonométrie), nous importons sqrt, c'est-à-dire la racine carrée. Nous en avons besoin pour lire la fonction y3.
Après cela, nous devons lire la plage de la fonction par x et l'étape avec laquelle nous parcourons cette plage. Pour cela, je vais utiliser la carte.
En tant que premier paramètre, cette fonction prend une fonction qui transforme en quelque sorte les données dont nous avons besoin, et comme deuxième argument, une sorte de feuille de données que nous devons traiter
from_x, to_x, pace_x = map(float, input("Enter the first and the last"\ " x-coordinates and a pace dividing them by a"\ " space:").split())
Nous lisons les trois valeurs saisies dans un espace, les divisons en éléments par un espace (en utilisant la méthode de fractionnement, qui, lorsqu'elle est appelée sans paramètres, divisera automatiquement la chaîne que vous spécifiez par des espaces). Les données entrées à l'aide de input () seront par défaut de type str, c'est-à-dire une chaîne, nous n'aurons donc aucune erreur ici.
Étant donné que les numéros de limites de plage peuvent être fractionnaires, nous convertissons chaque élément du tableau résultant en un nombre réel à l'aide de la fonction float.
Notez que les variables sont déclarées sans spécifier de type de données. Il est déterminé automatiquement (le type de données de la valeur que vous essayez d'affecter à une variable), ou à l'aide des fonctions str, int, float, etc. défini manuellement par des variables, en appliquant ces mêmes fonctions aux valeurs. La même variable peut avoir un type de données différent tout au long du programme - attribuez-lui simplement une nouvelle valeur avec un type de données différent.
Par exemple
auxiliary_variable = ""
Revenons à notre programme. Nous devons vérifier si les données saisies sont correctes.
Le programme doit imprimer que les données saisies sont incorrectes si:
- l'étape est 0
- la limite inférieure de la plage est supérieure à la limite supérieure et le pas est positif (c'est-à-dire que nous avons une progression arithmétique de la forme xn = from_x + pace_x * (n - 1) , dans laquelle de_x> à_x . Depuis pace_x> 0, cette progression augmentera et nous ne jamais to_x )
- la limite inférieure de la plage est inférieure à la limite supérieure et le pas est négatif (raisonnement similaire)
- les graphiques composés d'un point ne sont pas informatifs, donc le segment sur lequel nous construisons la fonction doit contenir au moins deux valeurs
Nous formulons ces conditions dans le code. De toute évidence, le premier élément est facile à régler. Le deuxième et le troisième peuvent être combinés en un, si vous remarquez que le signe de la différence entre le premier (from_x) et le dernier (to_x) doit coïncider avec le signe du pas. Eh bien, le quatrième point n'est pas aussi compliqué: le module de la différence des première et dernière valeurs ne doit pas être inférieur au module de pas.
En raison du module, nous pouvons avoir une situation dans laquelle les signes de la différence et l'étape ne coïncident pas, mais la deuxième condition coupera ces cas, donc la condition est correcte.
Par conséquent, ces trois conditions ressembleront à ceci:
if (pace_x != 0) and (to_x - from_x)*pace_x >= 0 and abs(to_x - from_x):
Nous passons directement au tableau. Pour faciliter le débogage, je vais créer plusieurs variables avec des noms parlants qui seront responsables de la précision des nombres, du nombre d'espaces avant le nombre, du nombre d'espaces après le nombre, etc.
dials_precision = "%10.6g"
Alors qu'est-ce qui se passe ici?

dials_precision = "%10.6g"
dans cette ligne, je règle la précision du nombre. Maximum 10 caractères pour le nombre entier et 6 caractères pour la partie fractionnaire. Si nous avons une valeur trop grande pour cette plage, toutes sortes d'
e-15 ou quelque chose de similaire apparaîtront.
spaces_in_the_title = int((int(dials_precision[1:3])) / 2)
dials_precision est une chaîne, nous pouvons donc prendre une tranche de cette chaîne, c'est-à-dire une sorte de sous-chaîne. Dans ce cas, nous devons obtenir le nombre 10, donc nous prenons les caractères à 1 et 2 indices, nous convertissons cette sous-chaîne en un type de données entier, divisons par deux et arrondissons-le.
Nous avons besoin de cette variable pour que les inscriptions dans l'en-tête du tableau soient centrées sur la cellule
length_of_table_lower_bound = (int(dials_precision[1:3]) + 2) * 4 + 5
comme son nom l'indique, cette variable est responsable de la longueur des limites inférieures des cellules du tableau de valeurs de la fonction. Au total, le nombre occupe 10 positions, ce qui signifie que la colonne ne peut pas avoir moins de 10 de large. Lorsque nous obtenons des nombres au format e-15 (décrit ci-dessus), la valeur prend 11-12 positions. Par conséquent, à 10, nous ajoutons un autre diable.
4 est responsable du nombre de colonnes (x, y1, y2, y3) et 5 est du nombre de caractères qui limitent la cellule dans une ligne.
Les autres variables semblent intuitives, alors passons à l'impression de la plaque
print("|" + (spaces_in_the_title + 1) * delimiter + 'x' + spaces_in_the_title * delimiter + '|' + spaces_in_the_title * delimiter + "y1" +\ spaces_in_the_title* delimiter\ + '|' + spaces_in_the_title * delimiter + 'y2'\ + spaces_in_the_title * delimiter + '|' +\ spaces_in_the_title * delimiter\ + "y3" + spaces_in_the_title * delimiter + "|\n"\ + length_of_table_lower_bound * '-')
si nous connectons tout le code que nous avons déjà écrit, alors dans la console, nous verrons ceci:
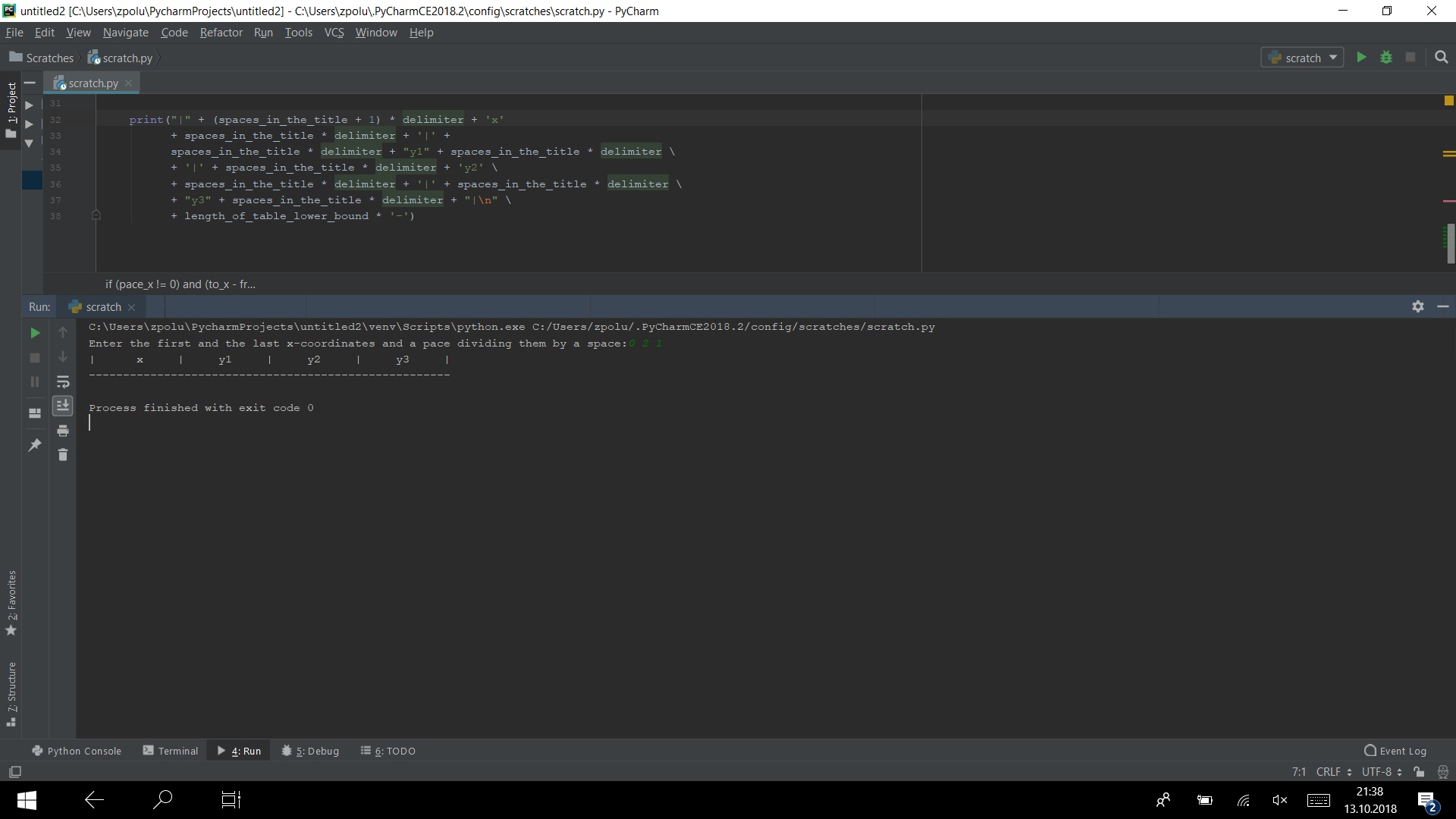
Maintenant, nous devons imprimer les valeurs elles-mêmes. Pour ce faire, vous avez besoin d'une boucle. Étant donné que les données saisies peuvent être fractionnaires, l'utilisation de la
plage ne fonctionnera pas, donc j'utiliserai une boucle régulière.
Comme nous pouvons avoir à la fois une séquence décroissante de X et une séquence croissante, les conditions de cycle doivent être définies de sorte que ces deux options soient prises en compte. Nous avons une variable créée précédemment qui stocke la réponse sur la nature de la séquence sous la forme de 0 ou 1. Par conséquent, il suffit de considérer deux cas et de sélectionner la condition appropriée pour chacun
while(is_sequence_decreasing and x_copy >= to_x) or\ (not is_sequence_decreasing and x_copy <= to_x):
Étant donné que pour le graphique, nous avons besoin du minimum et du maximum du graphique y1, que nous allons dessiner, nous introduisons des variables spéciales qui seront responsables de min et max
y1_cur_value = y1(x_copy) min_y1_value = (min_y1_value > y1_cur_value) * y1_cur_value + \ (min_y1_value <= y1_cur_value) * min_y1_value max_y1_value = (max_y1_value < y1_cur_value) * y1_cur_value + \ (max_y1_value >= y1_cur_value) * max_y1_value negative_value_exists += y1_cur_value < 0
la construction, en substance, répète la construction de
if: ... else: ... , uniquement à travers les inégalités booléennes.
y1_cur_value stocke la valeur actuelle de la fonction. J'ai créé une variable afin de ne pas appeler constamment une fonction lorsque sa valeur à un point est nécessaire.
Nous aurons également besoin de la présence de valeurs négatives pour le traçage.

Imprimez maintenant directement les valeurs. Je veux que tout soit beau et centré dans chacune des cellules, je dois donc traiter manuellement chaque valeur pour vérifier la longueur du nombre et sélectionner le nombre d'espaces en fonction pour aligner la valeur.
Remarque
Centrer littéralement le nombre ne fonctionnera pas. La variable responsable de la précision a le paramètre g. Il dit qu'un certain nombre de positions pour les nombres sont réservées à un nombre (dans notre cas, 10 par défaut). Si 10 chiffres ne sont pas composés, les positions vides seront situées à gauche des positions remplies. Par conséquent, nous ne pouvons centrer qu'une rangée de 10 positions.
aux_x = dials_precision % x_copy aux = len(aux_x) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_x) == int(dials_precision[1:3]) + 1 print('|' + delimiter * aux + aux_x + delimiter * (aux - aux_2) + '|', end='')
aux_x - une chaîne qui a déjà été amenée à une vue avec une précision donnée. Nous devons maintenant vérifier la longueur du nombre et sélectionner le nombre d'espaces requis. Étant donné que plus d'un espace de chaque côté n'est pas nécessaire, les variables
bool eva sont parfaites pour garder le nombre de ces mêmes espaces.
aux_2 intercepte le cas lorsque la longueur du nombre est 11.
Nous faisons aussi pour les valeurs de trois fonctions
aux_y1 = dials_precision % y1_cur_value aux = len(aux_y1) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y1) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y1 + delimiter * (aux - aux_2) + '|', end='') if (x_copy != 0): aux_y2 = dials_precision % y2(x_copy) aux = len(aux_y2) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y2) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y2 + delimiter * (aux - aux_2) + '|', end='') aux_y3 = dials_precision % y3(x_copy) aux = len(aux_y3) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y3) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y3 + delimiter * (aux - aux_2) + \ "|\n" + length_of_table_lower_bound * '-') else: print((spaces_in_the_title - 2) * delimiter + " " \ + (spaces_in_the_title - 2) * delimiter + '|' \ + (spaces_in_the_title - 2) * delimiter + " " \ + (spaces_in_the_title - 2) * delimiter + "|\n" \ + length_of_table_lower_bound * '-') x_copy += pace_x
Comme je l'ai dit au tout début, les deuxième et troisième fonctions ont des points de rupture - les deux fonctions n'existent pas au point x = 0. Par conséquent, nous devons également attraper ces cas.
Eh bien, n'oubliez pas d'augmenter la valeur x actuelle afin que nous n'obtenions pas un cycle sans fin.
Collectons tout le code dans un programme et exécutons-le, par exemple, sur le test -1,2 3,6 0,3
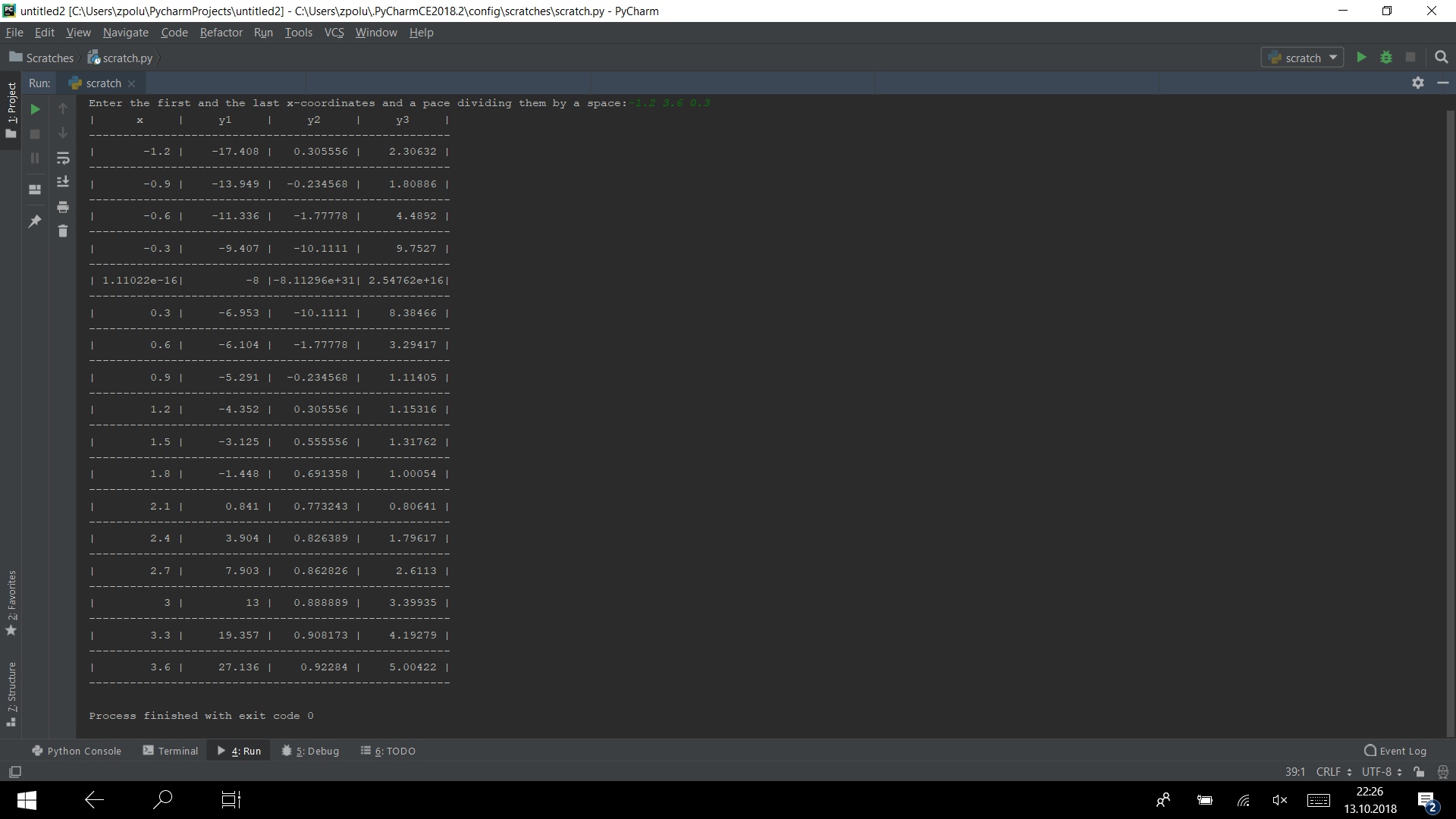
from math import sqrt def y1(x): return x**3 - 2*x**2 + 4*x - 8 def y2(x): return 1 - 1/x**2 def y3(x): return sqrt(abs(y1(x)*y2(x))) from_x, to_x, pace_x = map(float, input("Enter the first and the last"\ " x-coordinates and a pace dividing them by a"\ " space:").split()) if (pace_x != 0) and (to_x - from_x)*pace_x >= 0 and abs(to_x - from_x): dials_precision = "%10.6g"
Dans la deuxième partie de cette création, nous allons construire des graphes
 À suivre ...
À suivre ...