Jeu utilisant des graphiques mathématiques au lieu de graphiques

Dans cette capture d'écran, vous êtes présenté avec un jeu apparemment ordinaire avec des graphismes en pixels. Cependant, tout n'est pas si simple.

Le relief de la terre par endroits ressemble à une sinusoïde, et les balles sont similaires à deux graphiques symétriques de la racine de x.

En fait, tout ce que vous voyez à l'écran d'une manière ou d'une autre se rapporte aux mathématiques, aux courbes mathématiques et aux graphiques.

Contexte

Une fois, en regardant la vidéo de la chaîne "Numberphile", je suis tombé sur un matériel vidéo très intéressant appelé "The Formula of Everything" .

Dans cette vidéo, la formule autoréférentielle de Tapper a été présentée, qui, avec une certaine valeur de k, a recréé son image sur le graphique. Cette formule ressemble à ceci:

$$

$$\ frac {1} {2} <\ lfloor mod (\ lfloor \ frac {y} {17} \ rfloor 2 ^ {-17 \ lfloor x \ rfloor - mod (\ lfloor y \ rfloor, 17)}, 2 ) \ rfloor$$

Cette formule m'a vraiment intéressé et j'ai eu une idée:

"Et si vous créez un jeu où, au lieu de textures ordinaires stockées dans divers fichiers au format .png et .jpg, des graphiques et des courbes mathématiques seront utilisés?"

Cette idée m'a paru assez intéressante et difficile à mettre en œuvre.

Les tâches

J'ai fait face aux tâches suivantes:

• Trouvez le sens du jeu, le gameplay
• Dérivez des formules, dont les graphiques seront les silhouettes des personnages, des balles, des surfaces dont j'ai besoin
• Implémentez tout cela dans le jeu

Gameplay et signification du jeu

Le gameplay et la signification du jeu ont changé plusieurs fois au cours du développement de ce jeu. Tout cela parce qu'il y a eu quelques difficultés, en particulier, avec la dérivation de formules pour certaines silhouettes. Mais en général, ce jeu concerne une soucoupe volante solitaire qui vole autour des planètes, les explore et tue les ennemis qui se mettent sur son chemin.

Formules et leur implémentation ultérieure dans le jeu

J'ai combiné les deux paragraphes suivants en une seule sous-rubrique, car il n'est pas pratique de «sauter» entre une formule et sa mise en œuvre.

Pour créer le jeu, le langage de programmation c ++ et la bibliothèque SFML ont été choisis pour créer des fenêtres et dessiner quelque chose dessus.

Depuis que je suis à l'école et que je n'ai découvert que récemment ce qu'est une sinusoïde et à quoi elle ressemble, j'ai eu de gros problèmes avec la dérivation de diverses formules. Le plus souvent, cela s'est terminé par une simple sélection.

À la fin de l'article, il y aura un lien vers GitHub, où tout le code est publié. Dans l'article, seuls de petits morceaux de code seront donnés afin de ne pas le salir.

Surface de la planète

Pour la surface de la planète, j'ai dérivé la formule suivante:

$$

$$f (x) = | sin (x) |$$

Une formule assez simple, mais une fois mise en œuvre, il était nécessaire de contrôler la hauteur et la longueur d'une sinusoïde donnée. Aussi, pour éviter la courbure du relief, x est multiplié par π. Par conséquent, le code final ressemble à ceci:

int groundC = ceil(abs(sin(((i+1)*groundScale*M_PI)))*groundHeight); 

Texture de la planète dans l'espace

La texture de la planète se compose d'un cercle et d'un motif dessus. Le jeu propose 4 formules pour créer des motifs et 12 textures de planètes avec un motif différent. En fonction de l '"étape" de la formule, différents motifs sont créés. De plus, lors de la génération d'une planète, elle est définie de manière pseudo - aléatoire pour la couleur, la taille et la position dans l'espace.

Balles

Image d'une balle du jeu. La balle est retournée.

Pour les balles, une formule très simple a été choisie:

$$

$$\ sqrt {x}$$

L'intrigue de cette formule est reflétée en abscisse.

Protagoniste

Nous sommes donc arrivés aux formules les plus complexes.

J'ai déduit très difficilement la formule du protagoniste. Cela ressemble à ceci:

$$

$$\ sqrt {x ^ {\ frac {1} {2.8}} + x ^ {10.9-x ^ {9.3-x}}} - 0.3$$

Oui, une formule très tordue, très moche. Mais l'essentiel n'est pas la formule, le résultat principal.

Pour obtenir le résultat, au début, je voulais juste me déplacer le long de l'axe x avec une certaine étape, écrire les coordonnées y, puis connecter tous ces points, obtenant ainsi notre plaque. Mais ensuite, j'ai accidentellement fait un pas trop petit, et toute mon assiette se dessinait magnifiquement à l'exception de deux points d'extrémité, qui se sont finalement connectés. En conséquence, la plaque ressemble à ceci:



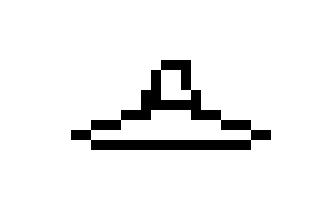
Ensuite, nous avions besoin de la texture du protagoniste dans l'espace. Cela ressemble à ceci:



C'était basé sur un cercle. La cabine principale est réalisée selon la formule suivante:

$$

$$(x ^ {7-x}) ^ {\ frac {0.8} {x}}$$

Le graphique de cette formule est mis en miroir le long de l'axe des ordonnées.

Voici à quoi ressemble cette formule en c ++:

 int x = round(pow(pow(i, 7 - i), 0.8 / i)); 

Les ennemis et leur géniteur

Sur la droite de l'image est un reproducteur bleu, les objets rouges sont des ennemis.

Spauner est une planète ordinaire avec un motif inhabituel. Ce modèle est un graphique de la formule:

$$

$$sin (x) * x ^ {0.8}$$

Formule de texture ennemie:

$$

$$(x ^ {3-x}) ^ {\ frac {1} {x}}$$

Les arbres

J'avoue, je ne pouvais pas dériver ou sélectionner une formule pour créer la silhouette des arbres. Mais, afin de ne pas violer le concept de base de l'ensemble du jeu et les règles de ne pas utiliser de fichiers au format .png et .jpg, j'ai utilisé une astuce. J'ai utilisé des fractales pour créer des arbres.


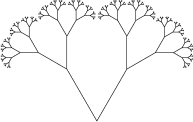Exemple d'arbre fractal

Vous conviendrez très probablement que les arbres fractals eux-mêmes semblent assez ennuyeux. Si vous ajoutez quelques éléments de hasard, par exemple, 2 branches peuvent ne pas nécessairement grandir, mais aussi 3 ou 1, ou pas du tout. De plus, il n'est pas possible de faire partout le même angle d'inclinaison.

Bien sûr, on pouvait faire une pseudorand machine ordinaire, qui était basée sur des ticks informatiques, mais l'idée suivante me semblait plus intéressante:

"Et que se passe-t-il si chaque arbre reçoit un nombre spécifique (graine) à partir duquel seront calculés des nombres pseudo-aléatoires qui affectent les paramètres de l'arbre?"

Heureusement, c ++ possède une bibliothèque de pseudo-protocoles distincte.

Par conséquent, les arbres générés ressemblent à ceci:



À gauche, un arbre avec la graine 13 et à droite - 22

Et le code qui génère ces arbres est:

 Branch Branch::createNewBranch(Branch cur, Tree* parent, float angleMultiplier, int level) { Vector2f sp(cur.startPoint.x, cur.startPoint.y); float randomAngle = ((*parent).getRand() * 15) - 5; float t = cur.thickness * 0.75; float l = cur.length * 0.67; float a = cur.angle + 30*angleMultiplier + randomAngle; sp.y -= (cos((cur.angle-180)*3.1415926 / 180) * cur.length); sp.x += (sin((cur.angle-180)*3.1415926 / 180) * cur.length); Branch gen(sp, t, l, a, level); if (level > 0) { int count = 100 * (*parent).getRand(); if (count >= 25 && count < 80) { //     ,      && count < 80,        ,  . , -          20%  10%,  ,    count<90 (*parent).addBranch(gen.createNewBranch(gen, parent, 1, level - 1)); (*parent).addBranch(gen.createNewBranch(gen, parent, -1, level - 1)); } if (count >= 80) { //    ,    count >= 90 if (count % 2 == 0) { (*parent).addBranch(gen.createNewBranch(gen, parent, -1, level - 1)); } else { (*parent).addBranch(gen.createNewBranch(gen, parent, 1, level - 1)); } } } return gen; } 

Remarque Oui, je sais que j'ai «codé en dur» certaines variables, mais ne m'en blâmez pas. Je pensais que cela n'avait aucun sens de créer des variables constantes distinctes, qui n'affectent en principe que les chances de créer une nouvelle branche.

Un peu plus de code

Ci-dessus, j'ai fourni du code uniquement pour générer des textures. Dans ce sous-titre, je décrirai le code du jeu lui-même. Tout le code est sur GitHub, le lien vers le projet est en conclusion.

Joueur

Le lecteur a deux méthodes de mise à jour différentes - spaceUpdate et planetUpdate. En conséquence, spaceUpdate met à jour le lecteur lorsqu'il est dans l'espace, planetUpdate - lorsqu'il est sur la planète. Sur la planète, l'accélération et la vitesse du joueur sont calculées. En fonction de l'accélération horizontale, l'angle d'inclinaison de la plaque passe de 30 degrés à -30. En approchant des barrières, la vitesse du joueur diminue. De telles barrières existent pour l'axe x (0; mapSize.x) et pour l'axe y. Pour l'axe y, les choses sont un peu plus compliquées. Il existe une hauteur minimale, qui est calculée comme suit: la hauteur minimale de la terre est prise, ajoutée à la hauteur de l'onde sinusoïdale et la hauteur des arbres est ajoutée. La hauteur des arbres est calculée de manière très simple - la longueur initiale de la branche multipliée par le nombre de cycles effectués lors de la génération de l'arbre. Il n'y a pas de bordure supérieure - volant hors de la carte par le haut, le joueur passe à spaceUpdate et l'espace est dessiné.

SpaceUpdate fonctionne comme suit: l'accélération et la vitesse du joueur sont calculées. Ensuite, l'angle de rotation du joueur est calculé. L'angle est calculé comme suit: si l'accélération est nulle, alors l'angle est calculé par rapport à la vitesse du joueur, sinon, par rapport à l'accélération. De plus, dans l'espace, le joueur a la possibilité de tirer. Le tir se déroule comme suit - une balle est créée avec une rotation comme celle d'un joueur et ajoutée à la liste. Lors de la mise à jour d'un joueur dans l'espace, chaque puce de cette liste est également mise à jour. Lors du rendu d'un joueur, des balles sont également dessinées. De plus, dans l'espace, les choses sont un peu plus compliquées avec des barrières. L'espace est divisé en secteurs, dans chaque secteur 4 planètes, au total - 1 000 000 de planètes et 25 000 secteurs. Chaque secteur a un identifiant unique. Si le reste lors de la division par 500 est égal à 0 - il y a une barrière gauche, si le reste de 499 est droit, si lors de la division par 500 le résultat est 0 - la barrière supérieure est présente, si 499 est la supérieure. S'il n'y a pas de barrières, alors en volant hors du cadre, le joueur se déplace vers le secteur correspondant.

L'espace

J'en ai déjà décrit la majeure partie, mais il reste encore certaines choses. Dans chacun des secteurs de l'espace, il y a 4 planètes. Quand un joueur appuie sur la touche E, s'il est à un rayon de cette planète, alors le joueur se déplace vers la planète.

Ennemis

L'IA des ennemis est très stupide - s'il y a un joueur dans le rayon de leur visibilité, alors ils ont simplement tendance à s'y écraser, et il y a une légère erreur, donc leur chemin est assez courbe. S'il n'y a pas de joueur dans le rayon de leur visibilité, ils sont envoyés à leur géniteur.

Générateur

Dans chaque secteur d'espace, il y a 1 géniteur. Les géniteurs peuvent être de tailles différentes. La taille affecte la visibilité du joueur. Si le joueur est dans sa zone de visibilité, le géniteur crée des ennemis toutes les 5 secondes, mais le nombre d'ennemis ne peut pas dépasser 10.

Conclusion

Après avoir passé environ une semaine, j'ai créé un jeu qui n'utilise aucun fichier .png ou .jpg.

Lien vers le projet sur GitHub

Pour ceux qui sont trop paresseux pour télécharger le projet et lancer le jeu, une courte vidéo sur le gameplay: