
Nous continuons notre connaissance du langage de programmation Julia, très jeune, mais incroyablement beau et puissant. La version bêta de six ans est enfin terminée, vous ne pouvez donc plus avoir peur des changements de syntaxe. Et tandis que tout le monde se demande s'il est bon ou mauvais de commencer l'indexation à partir d'une seule, la communauté agitée se débat activement: de nouvelles bibliothèques sortent, les anciennes sont mises à jour, des projets sérieux démarrent et les étudiants enseignent activement cette langue dans les universités. Alors ne soyons pas en reste! Nous rendons le thé plus fort, car nous allons coder cette nuit!
Préparation au travail
Ici, il y a une petite critique en russe, également sur le hub il y a une connaissance de la langue et des instructions d'installation . Encore une fois, en se concentrant sur la nécessité de Windows Management Framework , il y aura des problèmes avec le téléchargement de packages.
Après la mise à niveau, JuliaPRO inclut désormais uniquement Juno . Mais personnellement, j'aime davantage Jupyter : il n'y a eu aucun problème avec celui-ci sur l'ordinateur portable, en plus il est pratique de travailler dans le navigateur et de créer immédiatement des notes et des formules, en général, idéal pour créer des rapports, des diapositives ou des manuels.
Épouser Jupyter et Julia 1.0.1 Il existe plusieurs packages pour Julia, les plus réussis d'entre eux sont inclus dans les parcelles en tant que backends. Plots.jl - métalangage de la Plots.jl : c'est-à-dire une interface pour diverses bibliothèques de cartographie. Ainsi, Plots.jl interprète simplement vos commandes, puis crée des graphiques à l'aide d'une sorte de bibliothèque de graphiques. Ces bibliothèques graphiques d'arrière-plan sont appelées backends. La meilleure partie est que vous pouvez utiliser de nombreuses bibliothèques graphiques différentes avec la syntaxe Plots.jl , et nous verrons également que Plots.jl ajoute de nouvelles fonctionnalités à chacune de ces bibliothèques!
Installer des packages graphiquesPour installer des packages, exécutez les commandes dans REPL, Juno ou Jupyter:
# Pkg.add("Plots") # 0.7.0 julia>] pkg>add Plots pkg>add GR pkg>add PyPlot pkg>add Gadfly pkg>add PlotlyJS pkg>add UnicodePlots
Il n'est pas nécessaire d'installer tous les packages, mais sachez que chacun d'eux a ses propres caractéristiques . Je préfère plotlyjs () : bien qu'il ne diffère pas en vitesse, il est très interactif. Il y a un zoom, se déplaçant le long du plan, ainsi que la possibilité d'enregistrer le fichier, et si vous enregistrez le document Jupyter en html, toutes les fonctionnalités seront enregistrées. Vous pouvez donc ajouter au site ou faire une présentation interactive. Plus d'informations sur les pages: Plots , Gadfly
Motif premier sans fin
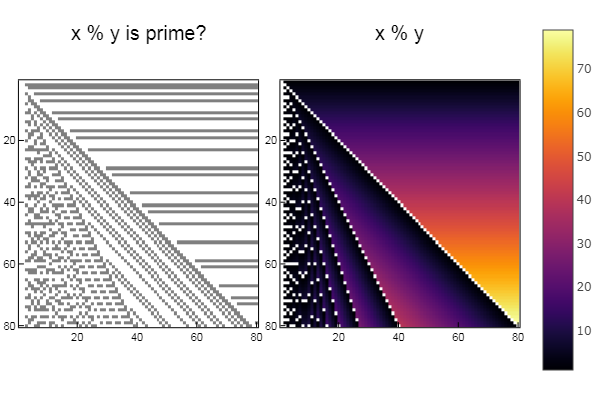
Mis en œuvre l'idée d'un article sur Habr . En quelques mots: que se passe-t-il si nous prenons les coordonnées du point et utilisons une opération, disons XOR ou ET au niveau du bit entre les abscisses et l'ordonnée, puis vérifions la simplicité du nombre ou l'appartenance aux nombres de Fibonacci, et si la réponse est oui, remplissez le point d'une couleur, et avec un négatif dans un autre? Vérifier:
Pour l'opération% using Plots plotlyjs() function eratosphen(n, lst) # ar = [i for i=1:n] ar[1] = 0 for i = 1:n if ar[i] != 0 push!(lst, ar[i]) for j = i:i:n ar[j] = 0 end end end end ertsfn = [] eratosphen(1000, ertsfn) # print(ertsfn) # print( size(ertsfn) ) # -> 168 N = 80 M = 80 W1 = [in( x % y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x % y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x % y is prime?") p2 = spy(W2, title = "x % y") plot(p1, p2, layout=(2),legend=false)
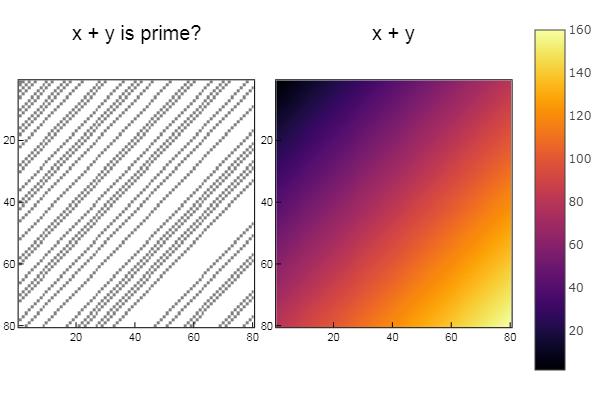
Pour l'opération + W1 = [in( x + y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x + y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x + y is prime?") p2 = spy(W2, title = "x + y") plot(p1, p2, layout=(2),legend=false)
Pour l'opération | W1 = [in( x | y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x | y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x | y is prime?") p2 = spy(W2, title = "x | y") plot(p1, p2, layout=(2),legend=false)

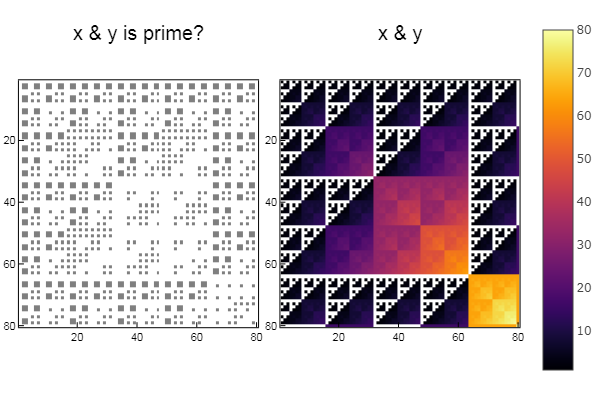
Pour le fonctionnement et W1 = [in( x & y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x & y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x & y is prime?") p2 = spy(W2, title = "x & y") plot(p1, p2, layout=(2),legend=false)
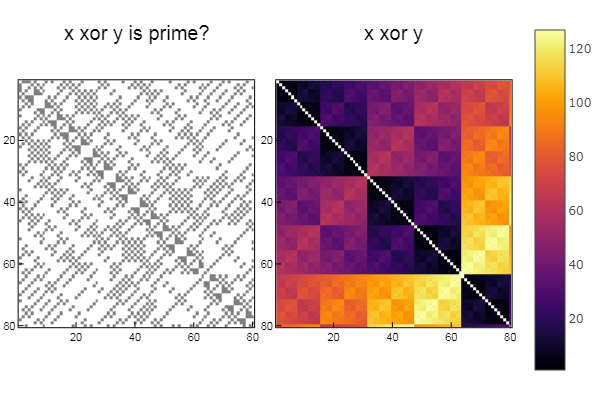
Pour l'opération xor W1 = [in( xor(x, y), ertsfn) for x = 1:N, y = 1:M]; W2 = [xor(x, y) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x xor y is prime?") p2 = spy(W2, title = "x xor y") plot(p1, p2, layout=(2),legend=false)
Et maintenant tout est pareil, mais pour les nombres de FibonacciVous pouvez faire une série comme d'habitude avec quelque chose comme:
function fib(n) a = 0 b = 1 for i = 1:n a, b = b, a + b end return a end fbncc = fib.( [i for i=1:10] )
Mais utilisons la représentation matricielle ( plus en détail ):
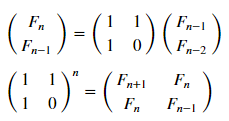
matr_fib = n -> [1 1; 1 0]^(n-1) # , n-1 mfbnc = [ matr_fib( i )[1,1] for i=1:17]; # 1,1 n- N = 100 M = N W1 = [in( x % y, mfbnc) for x = 1:N, y = 1:M]; W2 = [in( x | y, mfbnc) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x % y ∈ fibonacci?") p2 = spy(W2, title = "x | y ∈ fibonacci?") plot(p1, p2, layout=(2),legend=false)
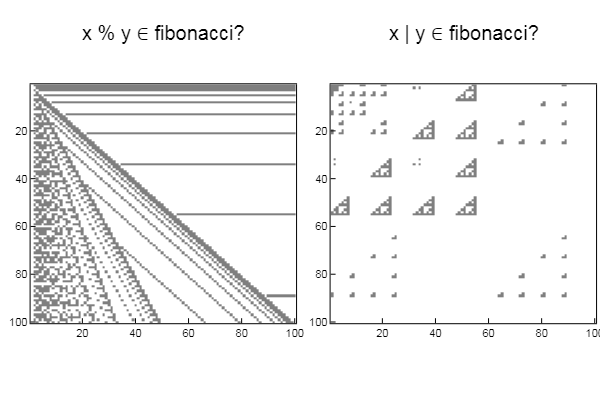
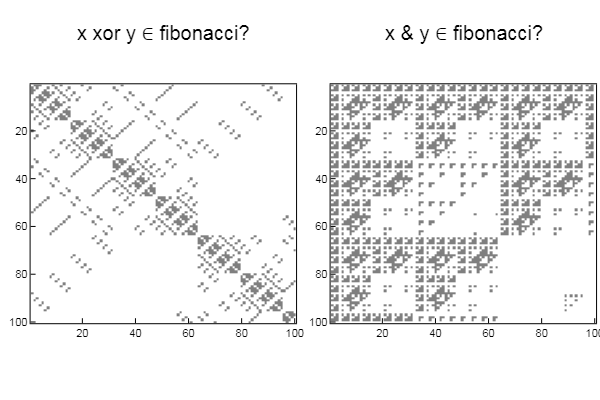
W1 = [in( xor(x, y), mfbnc) for x = 1:N, y = 1:M]; W2 = [in( x & y, mfbnc) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x xor y ∈ fibonacci?") p2 = spy(W2, title = "x & y ∈ fibonacci?") plot(p1, p2, layout=(2),legend=false)
Reflet d'une figure relativement droite
Ce type d'affichage est déterminé par la matrice:
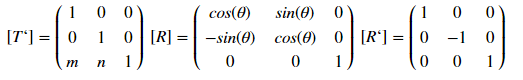
où [T '], [R] et [R'], respectivement, les matrices de déplacement, de rotation et de réflexion. Comment ça marche? Analysons un exemple de décalage - pour un point avec des coordonnées (x, y), le décalage de m par x et de n par le jeu sera déterminé par la transformation:
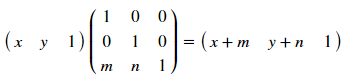
Ces matrices permettent des transformations pour différents polygones, l'essentiel est d'enregistrer les coordonnées les unes sous les autres et de ne pas oublier la colonne unitaire à la fin. Ainsi [T]:
- décale la ligne à l'origine avec le polygone en cours de transformation
- le fait pivoter pour coïncider avec l'axe X
- reflète tous les points du polygone par rapport à X
- suivi d'une rotation inverse et d'un transfert
Le sujet est décrit plus en détail dans le livre Rogers D., Adams J. Mathematical Foundations of Computer Graphics
Maintenant, codez-le!
using Plots plotlyjs() f = x -> 0.4x + 2 # # X = [2 4 2 2]' Y = [4 6 6 4]' xs = [-2; 7] # ys = f(xs) inptmtrx = [ XY ones( size(X, 1), 1 ) ] # m = 0 n = -f(0) # Y displacement = [1 0 0; 0 1 0; mn 1] a = (ys[2]-ys[1]) / (xs[2]-xs[1]) # θ = -atan(a) rotation = [cos(θ) sin(θ) 0; -sin(θ) cos(θ) 0; 0 0 1] reflection = [1 0 0; 0 -1 0; 0 0 1] T = displacement * rotation * reflection * rotation^(-1) * displacement^(-1) # outptmtrx = inptmtrx * T plot( X, Y) plot!( xs, ys ) plot!( outptmtrx[:,1], outptmtrx[:,2] )
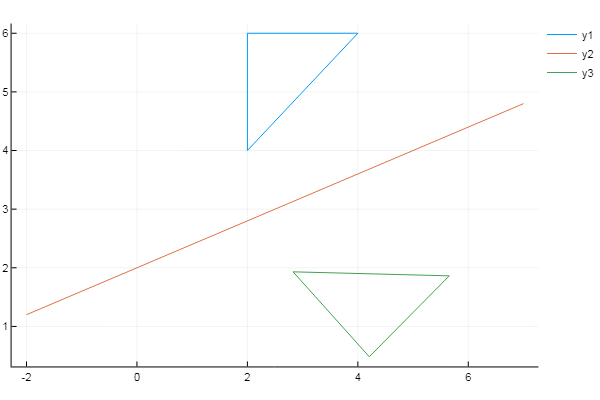
Fait intéressant: si vous vous débarrassez des caractères grecs et remplacez la première ligne par
function y=f(x,t) y=0.4*x + 2 endfunction,
Étant donné que les crochets [] encadrent les index des tableaux sur () et les radeaux sur plot( X, Y, xs, ys, trianglenew(:,1), trianglenew(:,2) ) , ce code est tout à fait lancé dans Scilab .
Travailler avec des graphiques en trois dimensions
Certains de ces packages prennent en charge la construction de graphiques en trois dimensions. Mais je voudrais mentionner séparément l'outil de visualisation plutôt puissant de Makie , qui fonctionne en conjonction avec les packages GLFW et GLAbstraction qui implémentent les fonctionnalités OpenGL dans julia. Plus d'informations sur Makie . Nous cachons son approbation sous
spoiler using Makie N = 51 x = linspace(-2, 2, N) y = x z = (-x .* exp.(-x .^ 2 .- (y') .^ 2)) .* 4 scene = wireframe(x, y, z) xm, ym, zm = minimum(scene.limits[]) scene = surface!(scene, x, y, z) contour!(scene, x, y, z, levels = 15, linewidth = 2, transformation = (:xy, zm)) scene
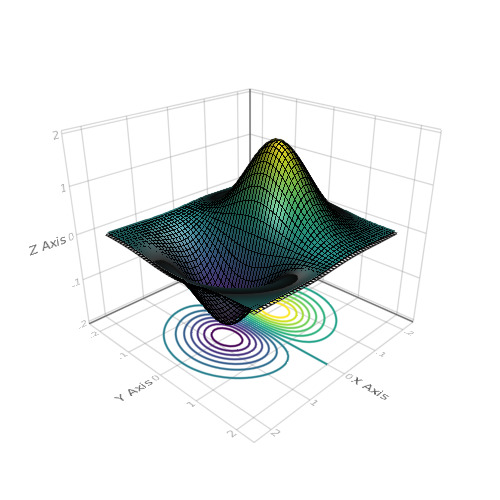
wireframe(Makie.loadasset("cat.obj"))

using FileIO scene = Scene(resolution = (500, 500)) catmesh = FileIO.load(Makie.assetpath("cat.obj"), GLNormalUVMesh) mesh(catmesh, color = Makie.loadasset("diffusemap.tga"))

x = Makie.loadasset("cat.obj") mesh(x, color = :black) pos = map(x.vertices, x.normals) do p, n p => p .+ (normalize(n) .* 0.05f0) end linesegments!(pos, color = :blue)
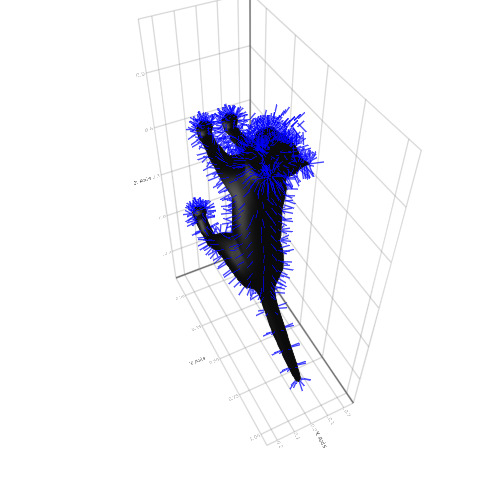
C'est tout avec les graphismes. Interactivité, animation, 3d, big data ou construction rapide de graphiques simples - des packages en constante évolution satisferont presque tous les goûts et besoins, et en plus, tout est très facile à apprendre. N'hésitez pas à télécharger des exercices pratiques et continuez à comprendre Julia!
UPD: Toutes les listes ci-dessus sont faites dans Jupyter avec julia 0.6.4. Malheureusement, certaines fonctions du méta-package Plots ont été supprimées ou renommées, nous continuons donc de surveiller les mises à jour, mais pour l'instant l'espion est complètement remplacé:
julia> using GR julia> Z = [x | y for x = 1:40, y = 1:40]; julia> heatmap(Z)