Début commencé
La dernière fois, j'ai décidé de construire une table de valeurs de fonction. Le moment est venu de procéder à la construction du calendrier lui-même, pour lequel tout cela a en fait commencé.
Donc, l'idée principale est la suivante. Faites pivoter l'axe des coordonnées de 90 degrés dans le sens des aiguilles d'une montre. Ceci est nécessaire afin de simplifier la construction sans stocker de données sur chaque point dans une feuille.
Ensuite, nous limitons l'axe des coordonnées du jeu à 82 caractères pour une meilleure lisibilité du graphique. Il est clair que ce faisant, nous perdons de la précision et le calendrier sera plus schématique (trop serré), en particulier pour les fonctions «cool», mais quand même.
Après cela, nous calculons la position de l'axe x par rapport à l'axe des joueurs, c'est-à-dire que nous cherchons à quel endroit nous aurons un point (x, 0). Eh bien, nous allons alors affecter ligne par ligne x la valeur de la fonction y1 à ce stade.
On y va
Tout d'abord, nous avons besoin de la formule suivante:

Nous donnerons 80 postes au planning lui-même, les deux places restantes seront purement décoratives. Avec cette formule, nous trouvons quelle plage de valeurs correspond à une position dans notre graphique. Ensuite, nous pouvons marquer correctement le point actuel dessus.
Les idées principales sont identifiées, alors passons au code lui-même
dial_length = 12 label = " y1 = x**3 - 2*x**2 + 4*x - 8" print("{1:>{0}}".format(len(label) + dial_length, label), '\n') print("{aux[1]:>{aux[0]}}\n {aux[2]:>{aux[0]}}>\n".format(aux = [dial_length + 82, 'y' , 82*'-']));
Notamment grâce aux commentaires de la première partie, j'ai appris une chose telle que le
format . Cela me semblait vraiment plus pratique que mes danses avec un tambourin, donc un énorme morceau de code de calcul des retraits s'est transformé en quelques lignes
print("{1:>{0}}".format(len(label) + dial_length, label), '\n')
L'unité est responsable du numéro de l'élément passé en argument à la fonction format, c'est-à-dire qu'il s'agit d'un «lien» (pas littéralement) vers la variable d'étiquette, que nous affichons en fait à l'écran. La numérotation est identique à celle des feuilles - à partir de zéro.
Une paire de caractères
:> est utilisée pour aligner le texte affiché sur le côté droit. Eh bien,
{0} après le caractère
> est nécessaire pour déterminer le nombre de positions de ligne dont vous avez besoin.
Autrement dit, dans ce cas, nous réservons pour les positions d'étiquette de ligne len (étiquette) + dial_length, et l'étiquette elle-même ne prend que len (étiquette), et nous alignons le texte sur le côté droit à l'intérieur de l'ensemble de ces positions.
print("{1:>{0}}".format(len(label) + dial_length, label), '\n') print(dial_length*' ' + label, '\n')
ces lignes sont équivalentes
Oui, pour les chaînes, il est probablement plus facile d'utiliser la deuxième option, mais appliquer la première pour le développement général ne fera pas de mal)
print("{aux[1]:>{aux[0]}}\n {aux[2]:>{aux[0]}}>\n".format(aux = [dial_length + 82, 'y' , 82*'-']));
Même les tableaux de type r_value (en C ++) peuvent être entassés dans un format, c'est-à-dire créés directement lors du passage d'un argument.
Nous fixons les variables qui sont constantes avec nous, c'est-à-dire qu'elles ne dépendent pas de la valeur actuelle de la fonction.
En python, il n'y a pas de constante conditionnelle pour désigner les constantes, il est donc habituel d'appeler de telles variables en majuscules et de ne pas les changer.
MAX_Y1_VALUE_DIFFERENCE = (max_y1_value - min_y1_value) + \ (max_y1_value == min_y1_value) RATIO = MAX_Y1_VALUE_DIFFERENCE / 80 AXIS_X_POS = abs(int((- min_y1_value) / RATIO)) if (AXIS_X_POS > 80): AXIS_X_POS = 81
Étant donné que RATIO pour des raisons évidentes ne peut pas être égal à 0, MAX_Y1_VALUE_DIFFERENCE doit être un nombre positif. C'est pourquoi le deuxième mandat se trouve à droite de la mission.
La position de l'axe des x que nous calculons par la formule

D'où vient cette formule? Nous calculons simplement le rapport des segments (sur l'axe du jeu) du début de l'axe (min (y1)) à la valeur actuelle de la fonction (y1 (x)) et du segment du début de l'axe jusqu'à sa fin (max (y1)). Eh bien, nous multiplions ce rapport par 80 pour trouver une telle distance entre le début de l'axe et la valeur actuelle dans les espaces (par conséquent, vous ne pouvez utiliser que des entiers), ce qui reflétera la formule du rapport sur le graphique.
Puisque nous sommes intéressés par la position à y1 (x) = 0, nous substituons les valeurs nécessaires et le tour est joué dans la formule.
Vous pouvez maintenant passer directement à l'impression des valeurs
while (is_sequence_decreasing and from_x >= to_x) or \ (not is_sequence_decreasing and from_x <= to_x): y1_cur_value = y1(from_x) cur_y1_value_and_min_difference = (y1_cur_value - min_y1_value) + \ (y1_cur_value == min_y1_value) * \ ((max_y1_value == min_y1_value)) pos_of_y = int(cur_y1_value_and_min_difference * 80 / \ MAX_Y1_VALUE_DIFFERENCE)
Le cycle nous est déjà familier. Nous devrons compter chaque valeur de la fonction une deuxième fois, afin de ne pas les stocker dans une feuille ou autre chose.
La position du jeu est calculée par la formule ci-dessus.
Nous devrons fixer la différence supérieure à la formule, en prévoyant le cas où dans la formule nous obtenons l'incertitude de la forme zéro par zéro. Si une telle incertitude survient, cela signifiera que la valeur actuelle est y1 (x) = max (y1), ce qui signifie que la valeur actuelle du jeu coïncidera avec la fin de l'axe y.
print("{1:^{0}.6g}".format(dial_length, from_x), end='') if (negative_value_exists): if y1_cur_value <= 0 - RATIO / 2: req_aux = AXIS_X_POS - pos_of_y if (req_aux != 0): print(pos_of_y * ' ' + '*' + (req_aux - 1) * ' ' + '|') else: print((AXIS_X_POS - 1) * ' ' + '*' + '|') elif y1_cur_value >= 0 + RATIO / 2: req_aux = pos_of_y - AXIS_X_POS if (req_aux != 0): print(AXIS_X_POS * ' ' + '|' + (req_aux - 1) * ' ' + '*') else: print((AXIS_X_POS) * ' ' + '|*') else: print(AXIS_X_POS * ' ' + '*') else: print('|' + pos_of_y* ' ' + '*') AXIS_X_POS = 0 from_x += pace_x print((dial_length + AXIS_X_POS) * ' ' + '|\n', (dial_length + AXIS_X_POS - 3) * ' ' + 'x V')
Cette partie du code est directement responsable de l'impression du graphique lui-même.
print("{1:^{0}.6g}".format(dial_length, from_x), end='')
Ici, le format était très utile et simplifiait le code.
^ nous permet d'aligner le nombre au centre de la zone sélectionnée (dans ce cas, 12 positions).
g est responsable des nombres - s'ils n'ont pas de partie fractionnaire, alors il ne sera pas imprimé (nombre comme entier), sinon - 6 décimales
Puisque notre graphique est limité à un espace de 80 caractères le long de l'axe y, sur notre graphique la valeur de la fonction au point coïncidera avec l'axe x non seulement dans le cas y1 (x) = 0, mais aussi dans le voisinage [0 - RATIO / 2, 0 + RATIO / 2].
Au total, nous avons trois cas d'agencement d'un astérisque (c'est-à-dire un point) et d'un bâton vertical (c'est-à-dire l'axe des x): '* |' (y1 (x) <= 0 - RATIO / 2), '*' (0 - RATIO / 2 <y1 (x) <0 + RATIO / 2), '| *' (y1 (x)> = 0 + RATIO / 2), nous considérerons ces trois cas.
- y1 (x) <= 0 - RATIO / 2
Dans ce cas, le point est situé sur l'axe des x, nous recherchons donc la distance du point à l'axe dans les espaces. En raison de l'arrondissement des nombres, il peut arriver que les valeurs des variables AXIS_X_POS et pos_of_y coïncident. Mais cela ne peut pas l'être, puisque dans ce cas nous serions dans le troisième cas. Dans notre cas, le point ne coïncide pas avec l'axe x, donc une condition supplémentaire est nécessaire, ce qui réduira de 1 la variable pos_of_y en cas d'égalité. - y (x)> = 0 + RATIO / 2
Le cas est identique au premier cas, seul le point sera situé de l'autre côté de l'axe x et toutes les actions ci-dessus sont ajustées pour cela - le reste
Le cas le plus simple - il suffit d'imprimer un astérisque à la place de l'axe
C'est si nous avons des valeurs négatives (y1 (x) <0). Sinon, tapez simplement '|' et déterminer la position du point.
Eh bien, nous terminons le programme avec un axe x supplémentaire.
Donc, le code qui a fini:
dial_length = 12 label = " y1 = x**3 - 2*x**2 + 4*x - 8" print("{1:^{0}.6f}".format(dial_length, x_copy)) print("{1:>{0}}".format(len(label) + dial_length, label), '\n') print("{aux[1]:>{aux[0]}}\n {aux[2]:>{aux[0]}}>\n".format(aux = [dial_length + 81, 'y' , 82*'-']), end=''); MAX_Y1_VALUE_DIFFERENCE = (max_y1_value - min_y1_value) + \ (max_y1_value == min_y1_value) RATIO = MAX_Y1_VALUE_DIFFERENCE / 80 AXIS_X_POS = abs(int((- min_y1_value) / RATIO)) if (AXIS_X_POS > 80): AXIS_X_POS = 81 while (is_sequence_decreasing and from_x >= to_x) or \ (not is_sequence_decreasing and from_x <= to_x): y1_cur_value = y1(from_x) cur_y1_value_and_min_difference = (y1_cur_value - min_y1_value) + \ (y1_cur_value == min_y1_value) * \ ((max_y1_value == min_y1_value)) pos_of_y = int(cur_y1_value_and_min_difference * 80 / \ MAX_Y1_VALUE_DIFFERENCE) print("{1:^{0}.6g}".format(dial_length, from_x), end='') if (negative_value_exists): if y1_cur_value <= 0 - RATIO / 2: req_aux = AXIS_X_POS - pos_of_y if (req_aux != 0): print(pos_of_y * ' ' + '*' + (req_aux - 1) * ' ' + '|') else: print((AXIS_X_POS - 1) * ' ' + '*' + '|') elif y1_cur_value >= 0 + RATIO / 2: req_aux = pos_of_y - AXIS_X_POS if (req_aux != 0): print(AXIS_X_POS * ' ' + '|' + (req_aux - 1) * ' ' + '*') else: print((AXIS_X_POS) * ' ' + '|*') else: print(AXIS_X_POS * ' ' + '*') else: print('|' + pos_of_y* ' ' + '*') AXIS_X_POS = 0 from_x += pace_x print((dial_length + AXIS_X_POS) * ' ' + '|\n', (dial_length + AXIS_X_POS - 3) * ' ' + 'x V')
Exécutez le programme sur plusieurs tests
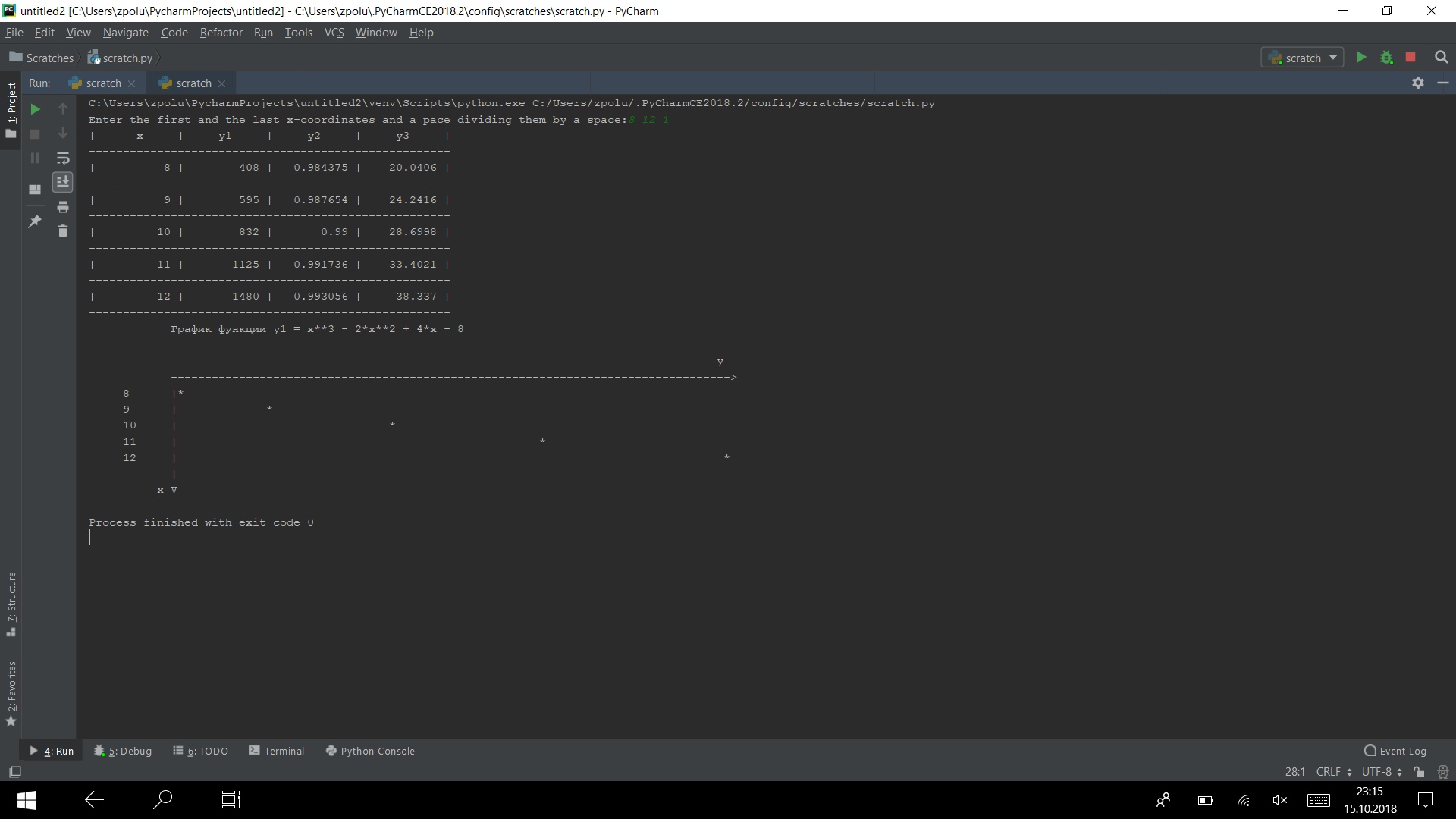
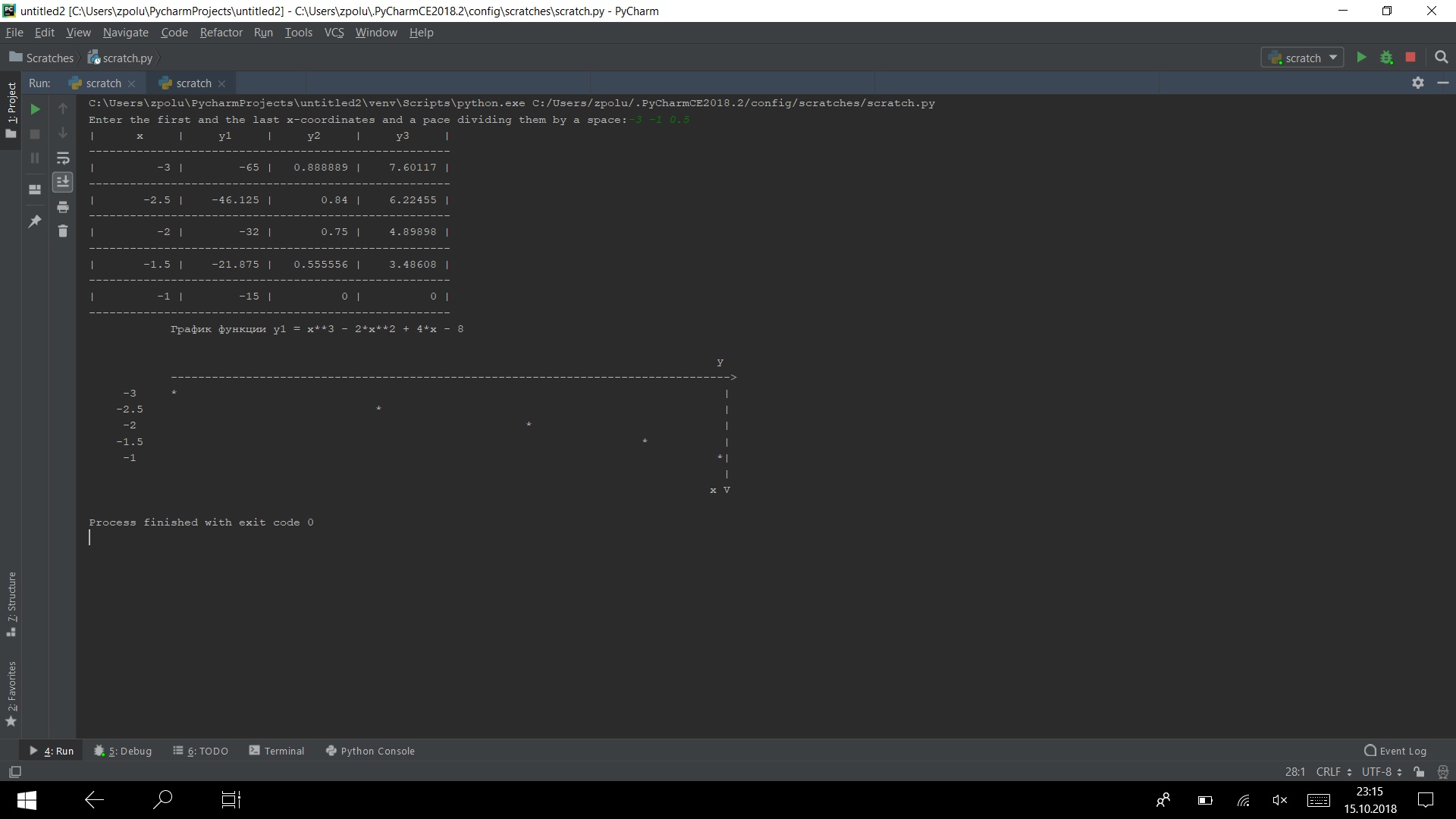
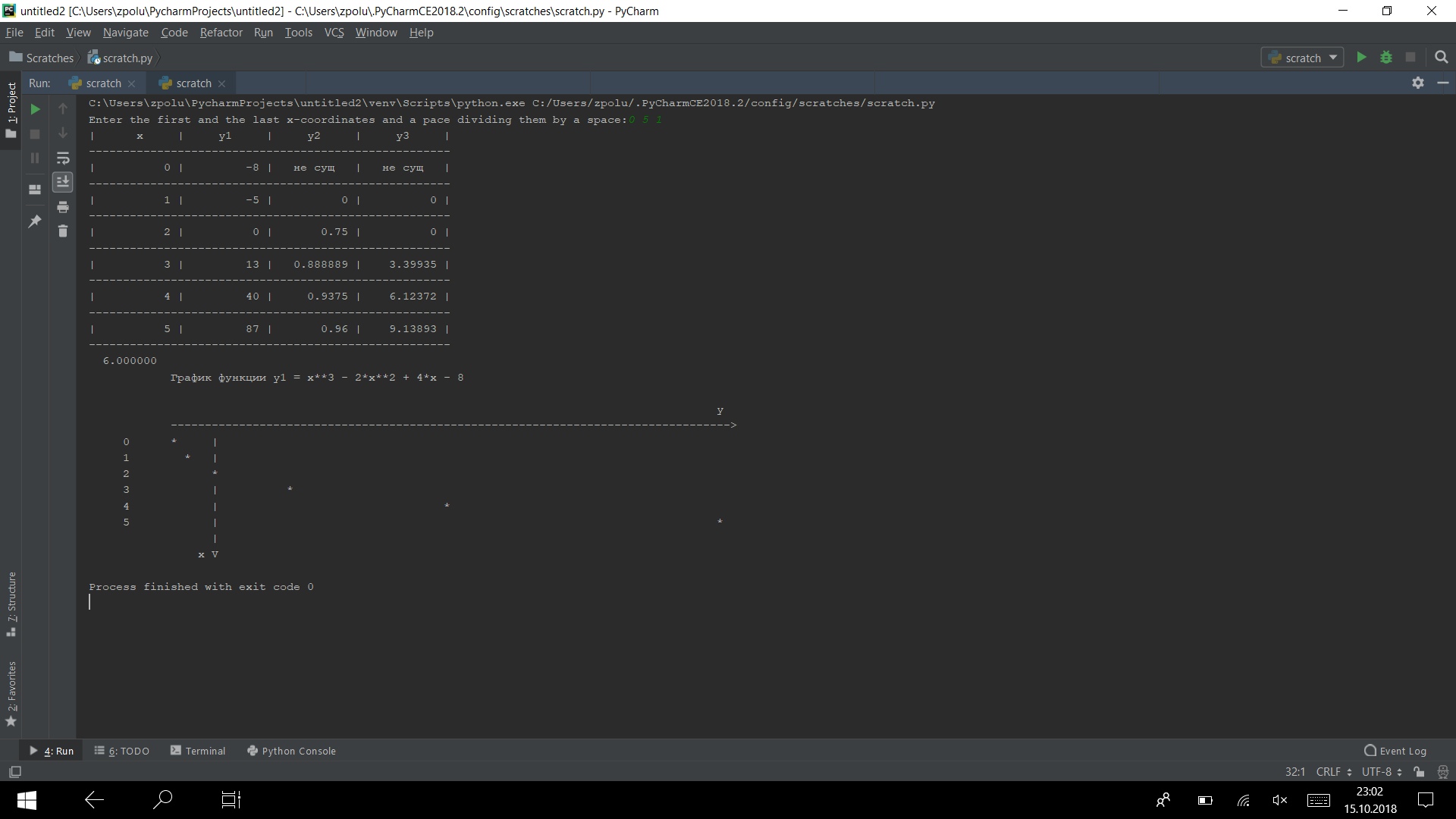
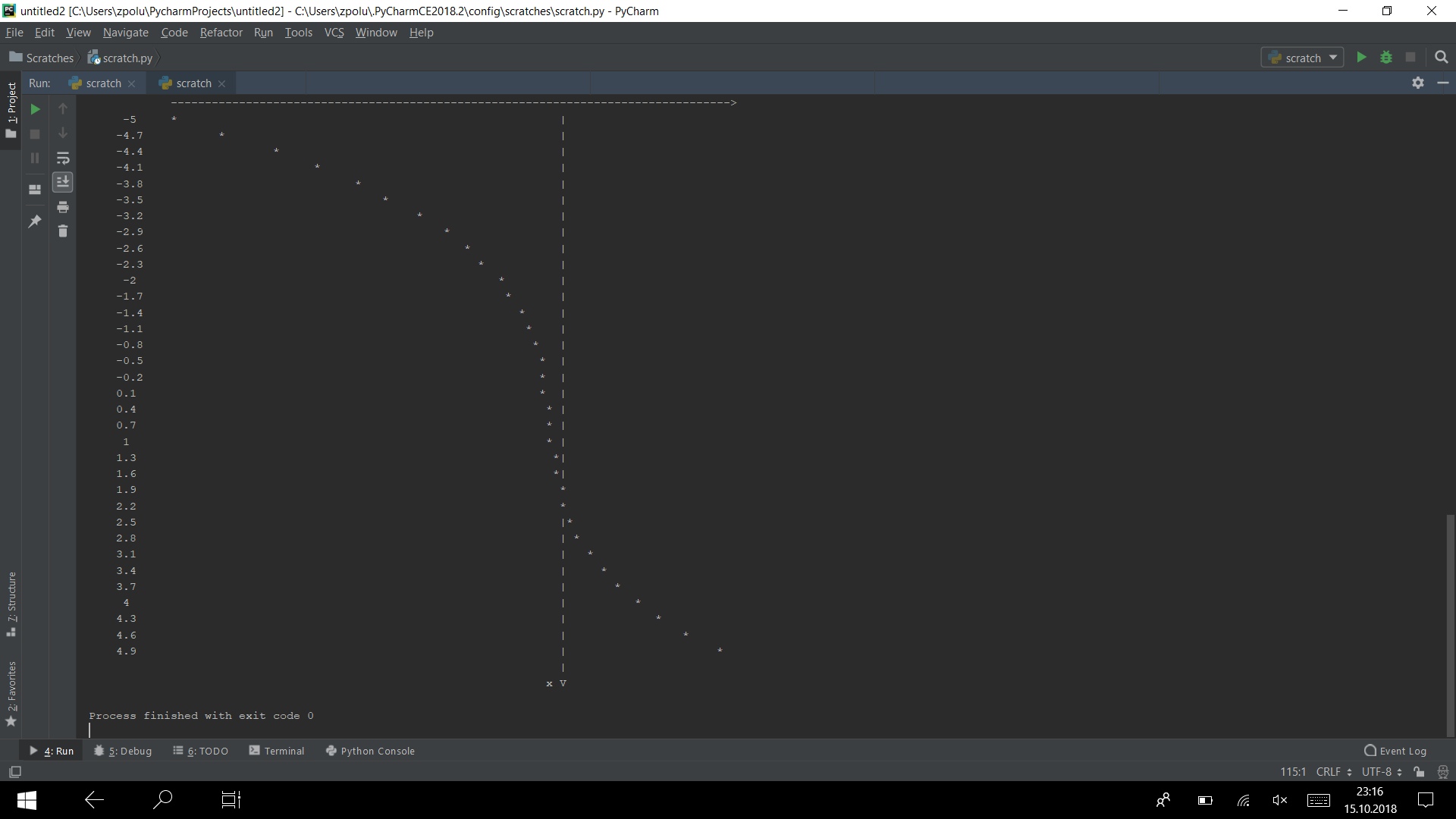
Ça marche)
