Spirale en rotation: mathématiques et hallucinations

Lorsque l'on essaie d'imaginer des hallucinations causées par des substances narcotiques, des formes psychédéliques tourbillonnantes et spirales ressemblant immédiatement à la vision en tunnel viennent à l'esprit. Mais de telles structures géométriques peuvent provoquer non seulement des médicaments hallucinogènes comme le LSD, le cannabis ou la mescaline . Les gens ont parlé de la survenue de telles visions au moment de leur mort, dans des conditions douloureuses telles que l'épilepsie et la schizophrénie, à la suite d' une privation sensorielle , ou même après une simple pression sur les globes oculaires. Ces hallucinations géométriques sont si répandues qu'au cours du siècle dernier, les scientifiques ont commencé à se demander s'ils pouvaient nous dire quelque chose de fondamental sur la structure de notre cerveau. Et, apparemment, ça l'est.


Constantes de formulaire créées sur un ordinateur. Les deux images du haut imitent l'entonnoir et la spirale qui se produisent après avoir reçu du LSD. Le coin inférieur gauche est le nid d'abeilles créé par la marijuana. Le coin inférieur droit est le Web.

Les hallucinations géométriques systématiques ont commencé à être étudiées dans les années 1920 par un psychologue américano-allemand, Heinrich Kluver . L'intérêt de Kluver pour la perception visuelle l'a finalement amené à expérimenter le peyote , un cactus, célébré par Carlos Castaneda , dont l'ingrédient psychoactif, la mescaline, a joué un rôle important dans les rituels chamaniques de nombreuses tribus d'Amérique centrale. La mescaline est bien connue pour provoquer des hallucinations visuelles vives. Utilisant du peyote en laboratoire avec un assistant, Kluver a remarqué la répétition de formes géométriques dans les hallucinations causées par la mescaline, et les a divisées en quatre types, les appelant des constantes de forme : tunnels et entonnoirs, spirales, treillis, qui comprennent des nids d'abeilles et des triangles, et des toiles d'araignées.

Dans les années 1970, les mathématiciens Jack Cowan et Bard Ermentraut ont utilisé la classification de Kluver pour créer une théorie qui décrit ce qui se passe dans le cerveau lorsqu'elle nous fait croire que nous voyons des motifs géométriques. Leur théorie a été développée par d'autres scientifiques, dont Paul Breslov, professeur de neurobiologie mathématique et informatique à l'Oxford Center for Collaborative Applied Mathematics récemment fondé.

Où sont les bandelettes du cortex cérébral *

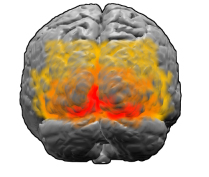Le cortex visuel. Zone marquée rouge V1

[ * Référence au conte de fées vietnamien «D'où vient le tigre de la bande» / env. perev. ]

La première zone du cortex visuel du cerveau qui traite les images chez l'homme et les mammifères est la zone connue sous le nom de V1. Des preuves expérimentales, telles que des images IRMf , suggèrent que les modèles de Kluver proviennent également principalement de V1 et n'apparaissent pas plus tard quelque part dans le système visuel. Comme le reste du cerveau, V1 a une structure complexe, ridée et pliée - cependant, il existe un moyen étonnamment simple de traduire ce que nous voyons dans notre champ de vision en l'activité des neurones dans V1. «Imaginez que nous déployons la V1», explique Breslov. - Il peut être imaginé comme un tissu nerveux de plusieurs millimètres d'épaisseur, avec différentes couches de neurones. Dans une première approximation, les neurones à travers la profondeur du cortex se comportent de manière similaire, donc si vous les aplatissez, vous pouvez imaginer V1 comme une feuille à deux dimensions. "

L'objet ou la scène du monde visuel est projeté sous la forme d'une image en deux dimensions sur la rétine de chaque œil, de sorte que ce que nous voyons peut également être considéré comme une feuille plate: champ de vision. Chaque point de cette feuille peut être désigné par deux coordonnées, comme un point sur la carte ou un point sur un modèle plat V1. Les zones alternées de lumière et d'obscurité qui composent les hallucinations géométriques sont causées par les zones alternées d'activité élevée et faible des neurones dans V1 - zones où les neurones sont activés très rapidement et zones où l'inverse est vrai.

Afin de traduire les modèles visuels en activité neuronale, une grille de coordonnées est nécessaire - une règle selon laquelle chaque point du champ de vision est connecté à un point du modèle plan V1. Dans les années 1970, des scientifiques, dont Cowen, ont réalisé une telle grille basée sur la connaissance de l'anatomie de l'interaction des neurones rétiniens avec les neurones de V1. Pour chaque partie claire ou sombre du champ de vision, la cartographie définit une partie d'activité neuronale élevée ou faible dans V1.

Comment cette imagerie de la rétine et du cortex transforme-t-elle les motifs géométriques de Kluver? Il s'avère que les hallucinations, provoquant des spirales, des cercles et des rayons émanant du centre, correspondent aux bandes d'activité des neurones de V1 passant à des angles donnés. Les réseaux tels que les nids d'abeilles ou les cellules correspondent aux modèles d'activité hexagonaux dans V1. Cela en soi n'est peut-être pas si intéressant, mais il existe un précédent: ce sont les rayures et les hexagones que les scientifiques ont observés lors de la modélisation d'autres exemples de formation de motifs, par exemple, la convection de liquides ou, plus surprenant, l'apparition de taches et de rayures sur la peau des animaux. Les mathématiques régissant la formation de ces motifs étaient bien connues et proposaient également un mécanisme de modélisation du fonctionnement du cortex visuel.

Du champ de vision au cortex visuel

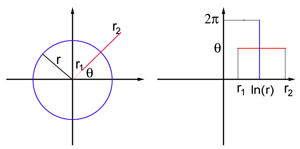
Imaginez le champ de vision sous la forme d'une feuille plate avec des coordonnées polaires: chaque point P est défini par deux nombres, (r, θ), où r est la distance à l'origine, et θ est l'angle entre le segment OP et l'axe x. Le point de référence correspond au centre du champ de vision. V1 est également modélisé comme une feuille plate, mais ayant cette fois des coordonnées cartésiennes (x, y). L'affichage exact des coordonnées du champ de vision et du modèle d'avion V1 est trop compliqué pour cet article, mais pour des points suffisamment éloignés du centre du champ de vision (c'est-à-dire pour un r suffisamment grand), il ressemble à une carte logarithmique:

$$

$$x = \ ln {r} \\ y = \ theta$$

La cartographie traduit un cercle de rayon r dans le champ de vision en un segment vertical droit avec x = ln r, et un rayon provenant de l'origine des coordonnées O à un angle θ en un segment horizontal droit avec y = θ

D'où vient la tache de léopard

Le premier modèle pour former des motifs de peau d'animal remonte à Alan Turing , mieux connu comme le père de l'informatique moderne et un hacker de Bletchley Park qui a déchiffré les codes. Turing s'est intéressé à la façon dont un système spatialement homogène tel qu'une boule uniforme de cellules, qui est l'embryon d'un animal, peut créer des motifs spatialement inhomogènes, mais statiques, tels que des rayures zébrées.

Turing a suggéré que ces modèles apparaissent à la suite d'un processus de réaction-diffusion . Imaginez un embryon animal dans la peau duquel vivent deux composés chimiques. L'un d'eux est un inhibiteur qui supprime la production de lui-même et d'un autre produit chimique. L'autre est un catalyseur qui provoque la production des deux substances.

Au moment initial du modèle de Turing, deux produits chimiques s'équilibrent idéalement - ils sont en équilibre et leur concentration en différents points de l'embryon ne change pas avec le temps. Imaginez maintenant que pour une raison quelconque, à un moment donné, la concentration de catalyseur a légèrement augmenté. Cette légère perturbation met l'ensemble du système en mouvement. La concentration locale accrue du catalyseur signifie que davantage de catalyseur et d'inhibiteur y sont produits. Cependant, les deux composés diffusent également sur la peau de l'embryon, inhibant et catalysant leur production à d'autres endroits.

Par exemple, si un inhibiteur diffuse plus rapidement qu'un catalyseur, il entourera rapidement le point de perturbation et réduira la concentration de catalyseur en lui. En conséquence, nous obtenons une section avec une concentration élevée de catalyseur, entourée d'une concentration élevée d'inhibiteur - en d'autres termes, une tache de catalyseur sur le fond de l'inhibiteur. En fonction du taux de diffusion des deux composés, il est possible qu'un tel motif tacheté apparaisse dans toute la peau de l'embryon, et finalement se stabilise.

Thuring a écrit un système d'équations différentielles décrivant la compétition entre les deux composés - vous pouvez les laisser se développer à temps et voir si des modèles apparaissent. Ces équations dépendent de paramètres décrivant le taux de diffusion de deux composés: si vous les sélectionnez correctement, le système finit par se stabiliser, formant un certain schéma qui peut être modifié en modifiant les paramètres. Le lien fournit une applet en Java , dans laquelle vous pouvez jouer avec les paramètres et regarder les modèles résultants.

Équations de motifs animaux

Pour simplifier, imaginez un embryon sous la forme d'une ligne unidimensionnelle. A tout instant t et en tout point x de l'embryon, la concentration du catalyseur (activateur) et de l'inhibiteur (inhibiteur) est déterminée par les fonctions A (x, t) et I (x, t). Ils évoluent dans le temps selon les règles suivantes:

$$

$$\ frac {\ partial A} {\ partial t} = f (A, I) + \ frac {\ partial ^ 2 A} {\ partial x ^ 2} \\ \ frac {\ partial I} {\ partial t } = g (A, I) + d \ frac {\ partial ^ 2 I} {\ partial x ^ 2}$$

Le premier terme à droite de chaque équation décrit la quantité de catalyseur et d'inhibiteur produite. Ce sont des fonctions des concentrations de catalyseur et d'inhibiteur, car les deux affectent la vitesse de réaction.

Le deuxième terme à droite de chaque équation est la dérivée seconde, qui décrit le taux de variation du gradient du catalyseur et de l'inhibiteur. Ils fixent le taux de diffusion.

Un terme supplémentaire d sur le côté droit de la deuxième équation est le coefficient de diffusion, qui montre combien l'inhibiteur diffuse plus rapidement que le catalyseur. Turing a montré que la supériorité de la vitesse de l'inhibiteur est un paramètre critique pour la génération de taches.

Modèles de cerveau

L'activité des neurones dans le cerveau n'est pas un processus de réaction diffuse, mais elle présente des analogies avec le modèle de Turing. «Les neurones s'envoient des signaux via des canaux de sortie de données appelés axones», explique Breslov. Les neurones réagissent aux signaux des autres, voici la réaction. «Les signaux voyagent si rapidement par rapport au processus de création de modèles qu'ils peuvent être confondus avec des interactions instantanées.» Par conséquent, au lieu de la diffusion, un processus local, nous avons une interaction instantanée à distance. Les rôles de catalyseur et d'inhibiteur sont joués par deux classes différentes de neurones. «Il existe des neurones excitateurs - qui augmentent la probabilité que d'autres neurones deviennent actifs - et il existe des neurones inhibiteurs qui réduisent cette probabilité», explique Breslov. «La compétition entre les deux classes de neurones est analogue au mécanisme catalyseur-inhibiteur du modèle de Turing.»


Motifs rayés, hexagonaux et rectangulaires d'activité nerveuse dans V1 générés par un modèle mathématique

Inspirés par les analogies des processus de Turing, Cowan et Ermentraut ont créé un modèle d'activité nerveuse en V1 en utilisant un ensemble d'équations formulées par Cowan et Hugh Wilson. Bien que les équations se soient révélées plus compliquées que celles de Turing, vous pouvez toujours jouer au même jeu, laissant le système évoluer au fil du temps et voir si des modèles d'activité nerveuse se développent. "Vous pouvez constater que dans certaines conditions, si vous augmentez le paramètre, représentant, par exemple, l'effet des médicaments sur le cortex, cela conduira à la croissance de schémas périodiques", explique Breslov.

Le modèle Cowan et Ermentraut suggère que les hallucinations géométriques résultent de l'instabilité dans V1: quelque chose, par exemple, la présence d'un médicament, supprime le réseau neuronal d'un état équilibré, amorçant un processus d'interaction croissante entre les neurones excitants et suppresseurs, qui se stabilise ensuite sous la forme de motifs rayés ou hexagonaux d'activité nerveuse dans V1. Ensuite, nous «observons» ce motif sous la forme de structures géométriques décrites par Kluver dans le champ de vision.

Symétries dans le cerveau

En fait, tout n'est pas aussi simple que dans les modèles Cowan et Ermentraut, car les neurones ne répondent pas seulement aux images claires et sombres. Par épaisseur V1, les neurones s'alignent dans des colonnes appelées hypercolonnes , chacune répondant approximativement à une petite partie du champ visuel. Mais tous les neurones de l'hypercolonne ne sont pas identiques: en plus de reconnaître les zones claires et sombres, chaque neurone est spécialisé dans la reconnaissance des visages locaux - lignes qui séparent les zones claires et sombres dans une partie de l'image - une certaine orientation. Certains reconnaissent des faces horizontales, d'autres - verticales, d'autres - des faces situées à un angle de 45 °, etc. Chaque hypercolonne contient des colonnes de neurones de toutes les orientations préférées; par conséquent, une hypercolonne peut répondre aux visages de toutes les orientations dans une certaine zone du champ visuel. C'est la composition d'hypercolonnes et de préférences d'orientation qui nous permet de reconnaître les contours, les surfaces et les textures du monde visuel.


Connexions dans V1: les neurones d'une hypercolonne interagissent avec la plupart des autres neurones. Mais ils ne réagissent avec les neurones dans d'autres hypercolonnes que si les colonnes sont situées dans le sens de leur orientation, et les neurones ont la même préférence d'orientation.

Ces dernières années, de nombreuses preuves anatomiques ont été recueillies sur la façon dont les neurones interagissent les uns avec les autres avec des préférences d'orientation différentes. À l'intérieur de leur géo-colonne, les neurones interagissent avec la plupart des autres neurones, quelles que soient leurs préférences. Mais, comme pour les neurones d'autres hypercolonnes, ils agissent de manière plus sélective, n'interagissant qu'avec des neurones de préférences similaires, afin de nous garantir la capacité de reconnaître des contours continus dans le monde visuel.

Breslov, en collaboration avec Cowen, le mathématicien Martin Golubitsky et d'autres scientifiques, a généralisé le modèle original de Cowen et Ermentraut pour prendre en compte ces nouvelles preuves anatomiques. Ils ont de nouveau utilisé le plan comme base du modèle V1: chaque hypercolonne est représentée sur le plan par un point (x, y), et chaque point (x, y) correspond à une hypercolonne. Les neurones avec une préférence donnée pour l'orientation θ (où θ est l'angle entre 0 et π sont indiqués par la position de l'hypercolonne (x, y) avec l'angle θ - c'est-à-dire qu'ils sont indiqués par trois unités d'information, (x, y, θ). Les modèles V1 ne sont pas un plan, mais un plan avec un ensemble complet d'orientations pour chaque point.


Si deux éléments, (x, y, θ) et (s, t, θ) interagissent, alors d'autres éléments de même orientation interagissent aux points (x + a, y + b) et (s + a, t + b ), et les éléments avec l'orientation -θ aux points (x, -y) et (s, -t).

Pour se conformer aux preuves anatomiques, Breslov et ses collègues ont suggéré que le neurone indiqué par le point (x ₀ , y ₀ , θ ₀ ) interagit avec tous les autres neurones dans la même hypercolonne (x ₀ , y ₀ ). Mais il n'interagit avec les neurones d'autres hypercolonnes que s'ils se trouvent dans son orientation préférée θ ₀ : sur le plan, vous devez tracer une ligne passant par le point (x ₀ , y ₀ ) selon un angle θ ₀ . Ensuite, les neurones désignés par le point (x ₀ , y ₀ , θ ₀ ) interagissent uniquement avec les neurones d'hypercolonnes situés sur la même ligne, c'est-à-dire ayant la même orientation préférée θ ₀ .

Ce schéma d'interaction est très symétrique. Par exemple, il ne change pas lorsque le plan est décalé dans n'importe quelle direction et sur n'importe quelle distance: si deux éléments, (x ₀ , y ₀ , θ ₀ ) et (s ₀ , t ₀ , φ ₀ ), interagissent, alors les éléments obtenus par le décalage, (x ₀ + a, y ₀ + b, θ ₀ ) et (s ₀ + a, t ₀ + b, φ ₀ ) pour certains a et b, interagissent de la même manière. Par le même principe, le schéma est invariant par rapport aux rotations et réflexions du plan.


Une hallucination en treillis créée par un modèle mathématique. Cela ressemble fortement aux hallucinations qui se produisent lors de la prise de marijuana.

Breslov et ses collègues ont utilisé une version généralisée des équations du modèle original pour permettre au système de se développer. Le résultat est un modèle qui est non seulement plus précis en termes d'anatomie de V1, mais également capable de générer des motifs géométriques dans le champ de vision dont le modèle d'origine n'était pas capable. Cela comprend les tunnels en treillis, les nids d'abeilles et les toiles d'araignées, dont l'orientation des contours les caractérise mieux que les zones contrastées claires et sombres.

De plus, le modèle est sensible aux symétries des schémas d'interaction des neurones: les mathématiciens ont montré que ce sont ces symétries qui génèrent la formation de schémas périodiques d'activité nerveuse. Par conséquent, le modèle suppose que les hallucinations donnent lieu à l'agencement d'hypercolonnes et de préférences d'orientation, c'est-à-dire de mécanismes qui nous aident à reconnaître les visages, les contours, les surfaces et les textures du monde visuel. C'est lorsque ces mécanismes perdent de leur stabilité, par exemple, à la suite d'une exposition au médicament, des schémas d'activité apparaissent qui se transforment en hallucinations visuelles.

Au-delà des hallucinations

Le modèle de Breslov permet non seulement de mieux comprendre les mécanismes qui génèrent des hallucinations visuelles, mais donne également des indices sur l'architecture du cerveau au sens large. Avec sa femme, un neurobiologiste expérimental, Breslov a étudié les contours des connexions hypercolonnes avec une vision normale afin de comprendre comment les images visuelles sont traitées. «Les gens ont l'habitude de croire que les neurones de la V1 définissent simplement des visages locaux, et qu'il faut aller à des niveaux supérieurs du cerveau pour collecter ces visages et reconnaître des choses plus complexes comme les contours et les surfaces. Mais à partir de notre travail avec ma femme, il est clair que ces structures en V1 permettent en fait au cortex visuel de reconnaître les contours à un stade précoce et d'effectuer un traitement plus global. On croyait que nous traitions des aspects de plus en plus complexes de l'image, en nous élevant plus haut dans la hiérarchie du cerveau. Maintenant, il est devenu clair qu'il existe une rétroaction active entre les parties supérieure et inférieure du cortex.«Ce n'est pas un processus hiérarchique simple, mais un système incroyablement complexe et actif, qui prendra plusieurs années à comprendre.»

Parmi les applications pratiques de ce travail, il y a la vision par ordinateur - les informaticiens construisent déjà des structures avec des connexions internes avec lesquelles Breslov et ses collègues ont joué pour construire des modèles pour enseigner aux ordinateurs comment définir les contours et les textures. Si vous faites preuve d'un peu d'imagination, vous pouvez imaginer que cette étude pourra un jour aider à restaurer la vision des personnes handicapées. «La question est de savoir s'il est possible de stimuler d'une manière ou d'une autre une partie du cortex visuel, en contournant l'œil, et de l'utiliser pour orienter les aveugles», explique Breslov. "Si vous comprenez comment le cortex est structuré et comment il réagit à la stimulation, alors il sera peut-être possible d'inventer la meilleure méthode pour sa stimulation correcte."

Il existe même de tels domaines d'application qui ne sont pas du tout liés au cerveau. Breslov a appliqué les idées obtenues par son travail à d'autres situations dans lesquelles des objets sont situés dans un espace avec une certaine orientation, par exemple, des fibroblastes de tissus humains et animaux. Il a montré que dans certaines conditions, ces cellules et molécules en interaction peuvent s'aligner et produire des motifs similaires à ceux qui apparaissent dans V1.

Les gens ont parlé de voir des hallucinations depuis le début des temps, et dans presque toutes les cultures - des images d'hallucinations peuvent même être trouvées dans des pétroglypheset peintures rupestres. Dans les traditions des chamans du monde entier, ils sont traités comme des messages du monde des esprits. Peu de neuroscientifiques modernes seront d'accord avec l'implication des esprits dans ce domaine, mais en tant que messagers du monde caché - cette fois, le monde caché de notre cerveau - ces hallucinations n'ont pas perdu leurs capacités.