
"Flou" chez les gens du commun est un effet de flou dans le traitement d'image numérique. Il peut être très efficace en soi, et en tant que composant d'animations d'interface, ou d'effets dérivés plus complexes (bloom / focusBlur / motionBlur). Avec tout cela, les bleus honnêtes sur le front sont plutôt lents. Et souvent, les implémentations intégrées à la plate-forme cible laissent beaucoup à désirer. Soit la vitesse est triste, les artefacts blessent les yeux. La situation donne lieu à de nombreuses mises en œuvre de compromis mieux ou moins bien adaptées à certaines conditions. Une implémentation originale avec une bonne qualité de fiabilité et la vitesse la plus élevée, tandis que la plus faible dépendance au matériel vous attend sous la coupe. Bon appétit!
(Flou de Laplace - Nom d'algorithme d'origine proposé)
Aujourd'hui, ma démoscène interne m'a donné des coups de pied et m'a forcé à écrire un article qui devait être écrit il y a six mois. En tant qu'amateur, à loisir, pour développer des algorithmes d'effets originaux, je voudrais proposer au public un algorithme de «blurah presque gausien», caractérisé par l'utilisation d'instructions de processeur exceptionnellement rapides (shift et masques), et donc accessible à l'implémentation jusqu'aux microcontrôleurs (extrêmement rapide dans un environnement limité).
Selon ma tradition d'écrire des articles sur Habr, je vais donner des exemples en JS comme le langage le plus populaire, et croyez-le ou non, c'est très pratique pour le prototypage rapide d'algorithmes. De plus, la possibilité de l'implémenter efficacement sur JS est venue avec des tableaux typés. Sur mon ordinateur portable pas très puissant, l'image plein écran est traitée à une vitesse de 30 images par seconde (le multithreading des travailleurs n'était pas impliqué).
Avis de non-responsabilité pour Cool MathsJe dirai tout de suite que je retire mon chapeau parce que je me considère comme n'étant pas suffisamment averti en mathématiques fondamentales. Cependant, je suis toujours guidé par l'esprit général d'une approche fondamentale. Par conséquent, avant de tromper mon approche quelque peu «observationnelle» de l'approximation, prenez soin de calculer la complexité en bits de l'algorithme, qui, comme vous le pensez, peut être obtenue par des méthodes d'approximation polynomiales classiques. J'ai deviné non? Vous vouliez les rapprocher rapidement? Étant donné qu'ils nécessitent une arithmétique flottante, ils seront considérablement plus lents qu'un décalage à un seul bit, ce que j'expliquerai à la fin. En un mot, ne vous précipitez pas vers l'intégrisme théorique et n'oubliez pas le contexte dans lequel je résous le problème.
Cette description est présente ici plutôt afin d'expliquer le cours de mes pensées et conjectures qui m'ont conduit au résultat. Pour ceux qui seront intéressés:
Fonction originale de Gauss:
g (x) = a * e ** (- ((xb) ** 2) / c), où
a est l'amplitude (si nous avons huit bits de couleur par canal, alors il = 256)
e est la constante d'Euler ~ 2,7
b - décalage graphique en x (nous n'avons pas besoin = 0)
c - paramètre affectant la largeur du graphique qui lui est associé comme ~ w / 2,35
Notre fonction privée (moins l'exposant supprimé avec le remplacement de la multiplication par division):
g (x) = 256 / e ** (x * x / c)
Que l'action d'approximation sale commence:
Notez que le paramètre c est très proche de la demi-largeur et défini sur 8 (cela est dû au nombre d'étapes que vous pouvez déplacer un canal de 8 bits chacun).
Nous remplaçons aussi grossièrement e par 2, cependant, notant que cela affecte la courbure de la «cloche» plus que ses bordures. En fait, cela affecte 2 / e fois, mais la surprise est que cette erreur compense le paramètre c, de sorte que les conditions aux limites sont toujours en ordre, et l'erreur n'apparaît que dans une «distribution normale» légèrement incorrecte, pour le graphique algorithmes, cela affectera la dynamique des transitions de dégradé de couleurs, mais il est presque impossible de le remarquer à l'œil nu.
Alors maintenant, notre fonction est la suivante:
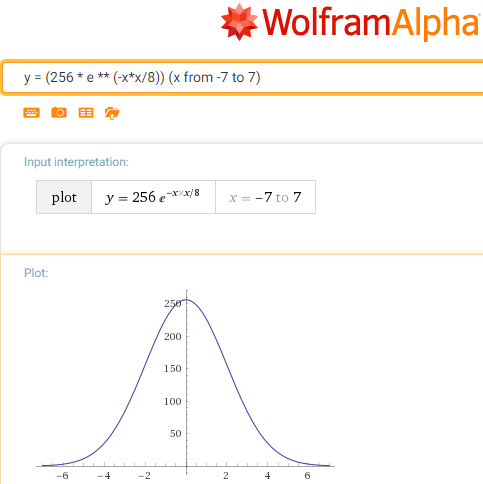
gg (x) = 256/2 ** (x * x / 8) ou gg (x) = 2 ** (8 - x * x / 8)
Notez que l'exposant (x * x / 8) a la même plage de valeurs [0-8] que la fonction d'un abs d'ordre inférieur (x), donc ce dernier est un candidat pour le remplacement. Nous allons rapidement vérifier la supposition en regardant comment le graphique change avec lui gg (x) = 256 / (2 ** abs (x)):
GaussBlur vs LaplasBlur:
Les écarts semblent trop importants, d'ailleurs, la fonction, ayant perdu son lissé, a maintenant un pic. Mais bon.
Tout d'abord, n'oublions pas que la régularité des gradients obtenus par le flou ne dépend pas de la fonction de densité de probabilité (qui est la fonction de Gauss), mais de son intégrale - la fonction de distribution. A cette époque, je ne connaissais pas ce fait, mais en fait, après avoir effectué une approximation «destructrice» par rapport à la fonction de densité de probabilité (Gauss), la fonction de distribution est restée assez similaire.
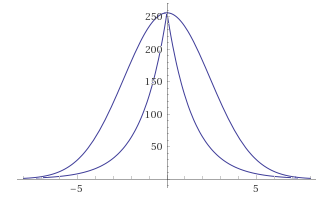
C'était:
C'est devenu:
La preuve, tirée de l'algorithme prêt à l'emploi, coïncide:
(Pour l'avenir, je dirai que l'erreur de flou de mon algorithme par rapport à Gausian x5 n'était que de 3%).
Nous nous sommes donc rapprochés beaucoup plus de la fonction de distribution de Laplace. Qui aurait pensé, mais ils peuvent laver les images à 97% pas pire.
Preuve, différences Gausian blura x5 et "Laplace blura" x7:

(ce n'est pas une image noire! Vous pouvez étudier dans l'éditeur)
L'hypothèse de cette transformation nous a permis de passer à l'idée d'obtenir la valeur par filtrage itératif, à laquelle j'avais prévu de réduire initialement.
Avant de dire un algorithme spécifique, il sera honnête de continuer et de décrire immédiatement son seul inconvénient (bien que la mise en œuvre puisse être corrigée avec une perte de vitesse). Mais cet algorithme est implémenté en utilisant l'arithmétique de cisaillement, et les puissances de 2 sont sa limitation. L'original est donc fait pour brouiller x7 (qui dans les tests est le plus proche de Gausian x5). Cette limitation d'implémentation est due au fait qu'avec une couleur à huit bits, en décalant la valeur dans le lecteur de filtre d'un bit par étape, toute action à partir du point se termine par un maximum de 8 étapes. J'ai également implémenté une version légèrement plus lente grâce à des proportions et des ajouts supplémentaires, qui implémente une division rapide par 1,5 (résultant en un rayon de x15). Mais avec l'application de cette approche, l'erreur augmente et la vitesse diminue, ce qui ne permet pas de l'utiliser comme ça. En revanche, il convient de noter que x15 est déjà suffisant pour ne pas remarquer la différence, le résultat est obtenu à partir de l'original ou de l'image sous-échantillonnée. La méthode est donc tout à fait appropriée si vous avez besoin d'une vitesse extraordinaire dans un environnement limité.
Ainsi, le cœur de l'algorithme est simple, quatre passes du même type sont effectuées:
1. La moitié de la valeur du lecteur t (initialement égale à zéro) est ajoutée à la moitié de la valeur du pixel suivant, le résultat lui est attribué. Continuez ainsi jusqu'à la fin de la ligne d'image. Pour toutes les lignes.
À la fin de la première passe, l'image est floue dans une direction.
2. Au deuxième passage, nous faisons de même dans la direction opposée pour toutes les lignes.
On obtient une image complètement floue horizontalement.
3-4. Maintenant, faites la même chose verticalement.
C'est fait!
Initialement, j'ai utilisé un algorithme à deux passes avec l'implémentation du back-flur à travers la pile, mais il est difficile à comprendre, pas gracieux, et il s'est avéré plus lent sur les architectures actuelles. Peut-être que l'algorithme en un seul passage sera plus rapide sur les microcontrôleurs, plus la possibilité de produire progressivement le résultat sera également un plus.
La méthode d'implémentation quadridirectionnelle actuelle, j'ai regardé Habré du précédent gourou sur les algorithmes de flou.
habr.com/post/151157 J'en profite pour lui exprimer ma solidarité et ma profonde gratitude.
Mais les hacks ne s'arrêtaient pas là. Maintenant, comment calculer les trois canaux de couleur dans une instruction de processeur! Le fait est que le décalage de bits utilisé comme division par deux vous permet de très bien contrôler la position des bits de résultat. Le seul problème est que les bits inférieurs des canaux glissent dans les plus hauts voisins, mais vous pouvez simplement les réinitialiser, puis résoudre le problème, avec une certaine perte de précision. Et selon la formule de filtre décrite, l'ajout de la moitié de la valeur du lecteur à la moitié de la valeur de la cellule suivante (sous réserve de réinitialiser les bits déchargés) ne conduit jamais à un débordement, vous ne devez donc pas vous en soucier. Et la formule de filtre pour le calcul simultané de tous les chiffres devient ceci:
buf32 [i] = t = (((t >> 1) & 0x7F7F7F) + ((buf32 [i] >> 1) & 0x7F7F7F);
Cependant, un ajout supplémentaire est nécessaire: il a été constaté expérimentalement que la perte de précision dans cette formule est trop importante, la luminosité de l'image saute visuellement de manière significative. Il est devenu clair que le bit perdu doit être arrondi à l'entier le plus proche et non jeté. Un moyen facile de le faire en arithmétique entière consiste à ajouter la moitié du diviseur avant la division. Notre diviseur est deux, vous devez donc en ajouter un, dans tous les chiffres, - la constante 0x010101. Mais avec tout ajout, il faut se méfier des débordements. Nous ne pouvons donc pas utiliser une telle correction pour calculer la moitié de la valeur de la cellule suivante. (S'il y a de la couleur blanche, nous obtiendrons un débordement, donc nous ne le corrigerons pas). Mais il s'est avéré que la principale erreur a été commise par plusieurs divisions de l'entraînement, que nous pouvons simplement corriger. Parce que, en fait, même avec une telle correction, la valeur dans le lecteur ne dépassera pas 254. Mais lorsqu'elle est ajoutée à 0x010101, le débordement ne sera pas garanti. Et la formule de filtre avec correction prend la forme:
buf32 [i] = t = ((((((0x010101 + t) >> 1) & 0x7F7F7F) + ((buf32 [i] >> 1) & 0x7F7F7F);
En fait, la formule effectue assez bien la correction, donc lorsque vous appliquez à plusieurs reprises cet algorithme à l'image, les artefacts commencent à être visibles uniquement dans les dix secondes suivantes. (pas le fait que la répétition du blura gausien ne produira pas de tels artefacts).
De plus, il y a une magnifique propriété avec de nombreux cols. (Cela n'est pas dû à mon algorithme, mais à la "normalité" de la distribution normale). Déjà au deuxième passage du Laplace Blura, la fonction de densité de probabilité (si j'ai bien compris) ressemblera à ceci:
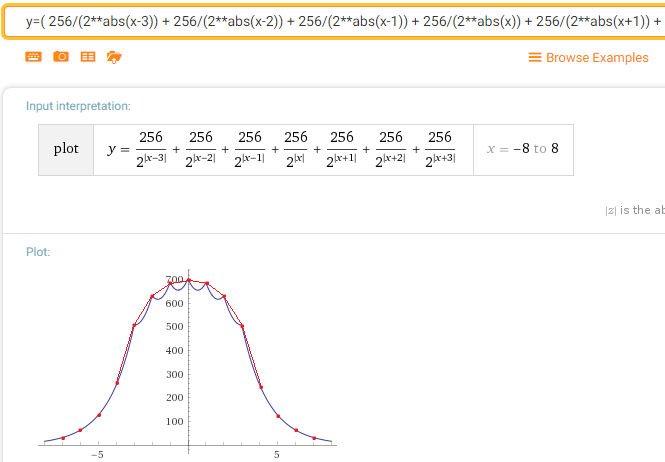
Ce qui, vous voyez, est déjà très proche de la gaussienne.
Empiriquement, j'ai trouvé que l'utilisation de modifications avec un grand rayon est autorisée par paires, car la propriété décrite ci-dessus compense les erreurs si la dernière passe est plus précise (la plus précise est l'algorithme de flou x7 décrit ici).
démorapcabillaudUn appel pour les mathématiciens sympas:
Ce qui serait intéressant de savoir à quel point il est correct d'utiliser un tel filtre séparément, je ne sais pas s'il y a une image de distribution symétrique. Bien que l'hétérogénéité de l'œil ne soit pas visible.
upd: Ici, je vais soulever des liens utiles, aimablement présentés par des commentateurs, et trouvés d'autres Khabrovites.
1. Fonctionnement des assistants Intel basés sur la puissance de SSE -
software.intel.com/en-us/articles/iir-gaussian-blur-filter-implementation-using-intel-advanced-vector-extensions (merci
vladimirovich )
2. Base théorique sur le sujet «Convolutions d'images rapides» + certaines de ses applications personnalisées en relation avec l'honnête
bleut gaussien -
blog.ivank.net/fastest-gaussian-blur.html (merci
Grox )
Les suggestions, commentaires, critiques constructives sont les bienvenus!