Vérification numérique de l'hypothèse abc (oui, celle-là)

Salut, Habr.

Il y a déjà eu plusieurs articles sur l'hypothèse abc au Geektimes Habr (par exemple, en 2013 et 2018 ). L'histoire elle-même d'un théorème qui ne peut être prouvé au départ pendant de nombreuses années, puis qui ne peut pas être vérifiée pendant le même nombre d'années, mérite certainement au moins un long métrage. Mais à l'ombre de cette merveilleuse histoire, le théorème lui-même est considéré trop superficiellement, bien qu'il n'en soit pas moins intéressant. Déjà au moins par le fait que l'hypothèse abc est l'un des rares problèmes non résolus de la science moderne, l'énoncé du problème que même un élève de cinquième année peut comprendre. Si cette hypothèse est vraiment vraie, elle découle facilement de la preuve d'autres théorèmes importants, par exemple la preuve du théorème de Fermat .

Sans revendiquer les lauriers de Motizuki, j'ai également décidé d'essayer et décidé de vérifier avec un ordinateur à quel point l'égalité promise dans l'hypothèse est remplie. En fait, pourquoi pas - les processeurs modernes ne sont pas seulement destinés à jouer à des jeux - pourquoi ne pas utiliser un ordinateur pour son objectif principal (calcul) ...

Peu importe ce qui s'est passé, s'il vous plaît, sous le chat.

Énoncé du problème

Commençons par le début. Quel est le théorème? Comme le dit Wikipedia (la formulation dans la version anglaise est un peu plus claire), pour les nombres mutuellement premiers (n'ayant pas de diviseurs communs) a, b et c tels que a + b = c, pour tout ε> 0, il y a un nombre limité de triplets a + b = c, tel que:



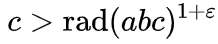
La fonction rad est appelée le radical et désigne le produit des facteurs premiers d'un nombre. Par exemple, rad (16) = rad (2 * 2 * 2 * 2) = 2, rad (17) = 17 (17 est un nombre premier), rad (18) = rad (2 * 3 * 3) = 2 * 3 = 6, rad (1 000 000) = rad (2 ^ 6 ⋅ 5 ^ 6) = 2 * 5 = 10.

En fait, l'essence du théorème est que le nombre de ces triplets est assez petit. Par exemple, si nous prenons au hasard ε = 0,2 et l'égalité 100 + 27 = 127: rad (100) = rad (2 * 2 * 5 * 5) = 10, rad (27) = rad (3 * 3 * 3) = 3, rad (127) = 127, rad (a * b * c) = rad (a) * rad (b) * rad (c) = 3810, 3810 ^ 1,2 est clairement supérieur à 127, l'inégalité ne tient pas. Mais il y a des exceptions, par exemple, pour l'égalité 49 + 576 = 625, la condition du théorème est remplie (ceux qui le souhaitent peuvent vérifier par eux-mêmes).

Le prochain moment clé pour nous est un nombre limité de ces égalités, selon le théorème. C'est-à-dire cela signifie que vous pouvez simplement essayer de tout trier sur un ordinateur. En conséquence, cela nous donne le prix Nobel une tâche de programmation assez intéressante.

Commençons donc.

Code source

La première version a été écrite en Python, et bien que ce langage soit trop lent pour de tels calculs, écrire du code dessus est facile et simple, ce qui est pratique pour le prototypage.

Obtenir le radical : nous décomposons le nombre en facteurs premiers, puis supprimons les répétitions, convertissant le tableau en un ensemble. Ensuite, obtenez simplement le produit de tous les éléments.

def prime_factors(n): factors = [] # Print the number of two's that divide n while n % 2 == 0: factors.append(int(2)) n = n / 2 # n must be odd at this point so a skip of 2 ( i = i + 2) can be used for i in range(3, int(math.sqrt(n)) + 1, 2): # while i divides n , print i ad divide n while n % i == 0: factors.append(int(i)) n = n / i # Condition if n is a prime number greater than 2 if n > 2: factors.append(int(n)) return set(factors) def rad(n): result = 1 for num in prime_factors(n): result *= num return result 

Nombres mutuellement premiers : factorisez les nombres et vérifiez simplement l'intersection des ensembles.

 def not_mutual_primes(a,b,c): fa, fb, fc = prime_factors(a), prime_factors(b), prime_factors(c) return len(fa.intersection(fb)) == 0 and len(fa.intersection(fc)) == 0 and len(fb.intersection(fc)) == 0 

Vérifiez : nous utilisons des fonctions déjà créées, tout est simple ici.

 def check(a,b,c): S = 1.2 # Eps=0.2 if c > (rad(a)*rad(b)*rad(c))**S and not_mutual_primes(a, b, c): print("{} + {} = {} - PASSED".format(a, b, c)) else: print("{} + {} = {} - FAILED".format(a, b, c)) check(10, 17, 27) check(49, 576, 625) 

Ceux qui le souhaitent peuvent expérimenter indépendamment en copiant le code ci-dessus dans n'importe quel éditeur de langage Python en ligne. Bien sûr, le code s'exécute comme prévu comme prévu et énumérer tous les triplets à au moins un million serait trop long. Sous le spoiler se trouve une version optimisée, il est recommandé de l'utiliser.

La version finale a été réécrite en C ++ en utilisant le multithreading et une certaine optimisation (travailler en C avec des ensembles qui se croisent serait trop hardcore, bien que probablement plus rapide). Le code source est sous le spoiler, il peut être compilé dans le compilateur gratuit g ++, le code fonctionne sous Windows, OSX et même sur le Raspberry Pi.


Pour ceux qui sont trop paresseux pour installer le compilateur C ++, une version Python légèrement optimisée est fournie, qui peut être exécutée dans n'importe quel éditeur en ligne (j'ai utilisé https://repl.it/languages/python ).

Résultats

Les triplets a, b, c sont vraiment très peu nombreux.

Quelques résultats sont donnés ci-dessous:
N = 10 : 1 «trois», délai <0,001 c
1 + 8 = 9

N = 100 : 2 «triples», durée d'exécution <0,001c
1 + 8 = 9
1 + 80 = 81

N = 1000 : 8 "triples", temps d'exécution <0,01c
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
3 + 125 = 128
13 + 243 = 256
49 + 576 = 625

N = 10000 : 23 "triples", temps d'exécution 2s


N = 100000 : 53 triplets, durée d'exécution 50c


Avec N = 1 000 000, nous n'avons que 102 "triplets", une liste complète est donnée sous le spoiler.


Hélas, le programme fonctionne toujours lentement, je n'ai pas attendu les résultats pour N = 10000000, le temps de calcul est supérieur à une heure (j'ai peut-être fait une erreur avec l'optimisation de l'algorithme quelque part, et je peux faire mieux).

Encore plus intéressant est de regarder graphiquement les résultats:



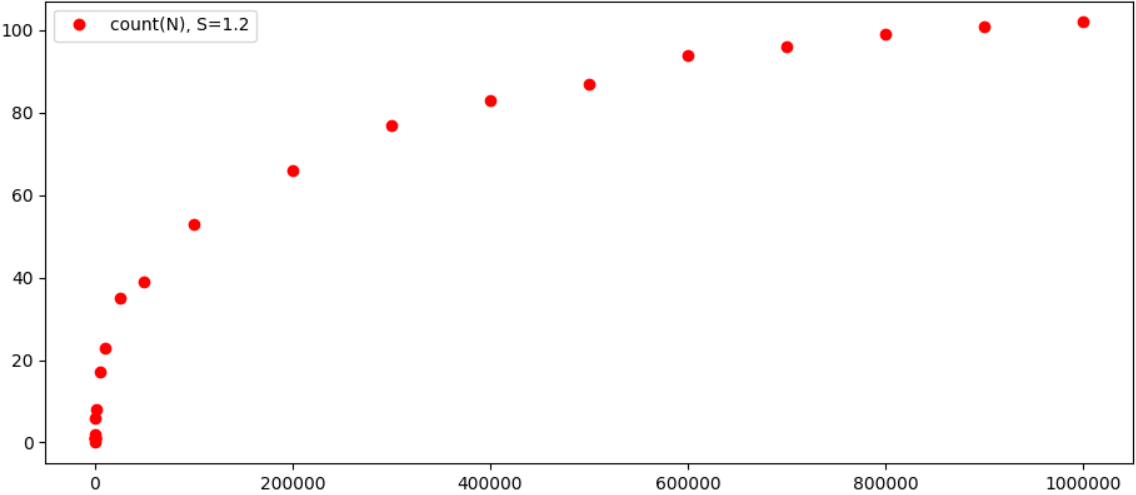
En principe, il est bien évident que la dépendance du nombre de triplets possibles de N croît sensiblement plus lentement que N lui-même, et il est probable que le résultat converge vers un certain nombre spécifique pour chaque ε. Soit dit en passant, avec une augmentation de ε, le nombre de triplets diminue sensiblement, par exemple, pour ε = 0,4, nous n'avons que 2 égalités pour N <100000 (1 + 4374 = 4375 et 343 + 59049 = 59392). Donc en général, il semble que le théorème tienne vraiment (enfin, et probablement il a déjà été testé sur des ordinateurs plus puissants, et peut-être que tout cela a longtemps été calculé).

Ceux qui le souhaitent peuvent expérimenter par eux-mêmes, si quelqu'un a des résultats pour les nombres de 10 000 000 et plus, je serai heureux de les ajouter à l'article. Bien sûr, il serait intéressant de «compter» jusqu'au moment où l'ensemble des «triplets» cesse complètement de croître, mais cela peut prendre très longtemps, la vitesse de calcul semble dépendre de N comme N * N (ou peut-être N ^ 3), et du processus très long. Néanmoins, une chose étonnante est à proximité, et ceux qui le souhaitent pourraient bien se joindre à la recherche.

Edit: comme suggéré dans les commentaires, Wikipédia a déjà un tableau avec les résultats - dans la plage N jusqu'à 10 ^ 18, le nombre de "triplets" continue d'augmenter, de sorte que la "fin" de l'ensemble n'a pas encore été trouvée. D'autant plus intéressant - l'intrigue est toujours préservée.