Plus récemment, j'ai dû résoudre une autre tâche de formation triviale de mon professeur. Cependant, en le résolvant, j'ai réussi à attirer l'attention sur des choses auxquelles je n'avais pas du tout pensé auparavant, peut-être que vous n'y avez pas pensé non plus. Cet article sera plus susceptible d'être utile aux étudiants et à tous ceux qui commencent leur voyage dans le monde de la programmation parallèle à l'aide de MPI.

Notre "Compte tenu:"
Ainsi, l'essence de notre tâche essentiellement informatique est de comparer le nombre de fois qu'un programme qui utilise des transferts point à point retardés non bloquants est plus rapide que celui qui utilise des transferts point à point bloquants. Nous effectuerons des mesures pour des matrices d'entrée de dimensions 64, 256, 1024, 4096, 8192, 16384, 65536, 262144, 1048576, 4194304, 16777216, 33554432 éléments. Par défaut, il est proposé de le résoudre par quatre processus. Et voici, en fait, ce que nous allons considérer:
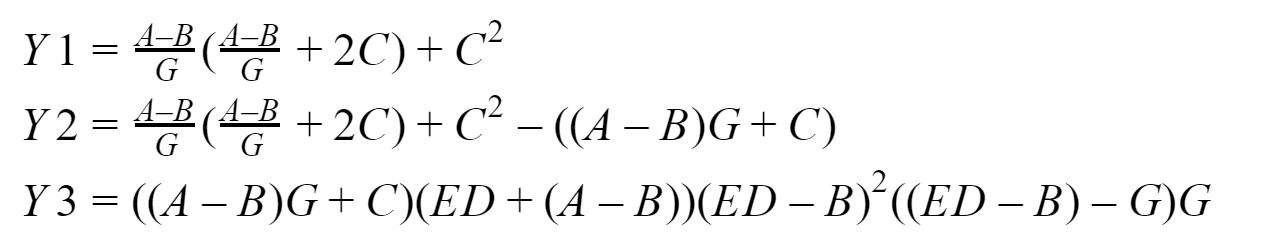
En sortie, nous devrions obtenir trois vecteurs: Y1, Y2 et Y3, que le processus zéro collectera. Je vais tester tout cela sur mon système basé sur
un processeur Intel avec 16 Go de RAM. Pour développer des programmes, nous utiliserons l'implémentation de la norme
MPI de Microsoft version 9.0.1 (au moment de la rédaction, c'est pertinent), Visual Studio Community 2017 et non Fortran.
Matériel
Je ne voudrais pas décrire en détail comment fonctionnent les fonctions MPI qui seront utilisées, vous pouvez toujours aller
consulter la documentation pour cela , donc je ne donnerai qu'un bref aperçu de ce que nous utiliserons.
Bloquer l'échange
Pour bloquer la messagerie point à point, nous utiliserons les fonctions:MPI_Send - implémente le blocage de l'envoi de messages, c'est-à-dire après avoir appelé la fonction, le processus est bloqué jusqu'à ce que les données qui lui sont envoyées soient écrites de sa mémoire dans la mémoire tampon du système interne MPI, après quoi le processus continue de fonctionner davantage;
MPI_Recv - effectue la réception du message de blocage, c'est-à-dire Après avoir appelé la fonction, le processus est bloqué jusqu'à l'arrivée des données du processus d'envoi et jusqu'à ce que ces données soient complètement écrites dans le tampon du processus de réception par l'environnement MPI.
Échange différé non bloquant
Pour la messagerie point à point non bloquante différée, nous utiliserons les fonctions:MPI_Send_init - en arrière-plan prépare l'environnement pour l'envoi de données qui se produiront dans un futur proche et sans verrouillage;
MPI_Recv_init - cette fonction fonctionne de manière similaire à la précédente, mais cette fois pour recevoir des données;
MPI_Start - démarre le processus de réception ou de transmission d'un message, il s'exécute également en arrière-plan de a.k.a. sans blocage;
MPI_Wait - est utilisé pour vérifier et, si nécessaire, attendre la fin de l'envoi ou de la réception d'un message, mais il bloque simplement le processus si nécessaire (si les données ne sont "pas envoyées" ou "non reçues"). Par exemple, un processus veut utiliser des données qui ne l'ont pas encore atteint - pas bon, donc nous insérons MPI_Wait devant l'endroit où il aura besoin de ces données (nous l'insérons même s'il y a simplement un risque de corruption de données). Un autre exemple, le processus a commencé le transfert de données en arrière-plan, et après avoir commencé le transfert de données, il a immédiatement commencé à modifier ces données d'une manière ou d'une autre - pas bon, donc nous insérons MPI_Wait devant l'endroit dans le programme où il commence à modifier ces données (ici nous l'insérons également même si il y a simplement un risque de corruption des données).
Ainsi,
sémantiquement, la séquence d'appels avec un échange non bloquant différé est la suivante:
- MPI_Send_init / MPI_Recv_init - préparer l'environnement pour la réception ou la transmission
- MPI_Start - démarrer le processus de réception / transmission
- MPI_Wait - nous appelons au risque de dommages (y compris "sous-envoi" et "sous-déclaration") des données transmises ou reçues
J'ai également utilisé
MPI_Startall ,
MPI_Waitall dans mes programmes de test, leur signification est essentiellement la même que MPI_Start et MPI_Wait, respectivement, seulement ils fonctionnent sur plusieurs packages et / ou transmissions. Mais ce n'est pas toute la liste des fonctions de démarrage et d'attente, il existe plusieurs autres fonctions pour vérifier l'intégralité des opérations.
Architecture inter-processus
Pour plus de clarté, nous construisons un graphique pour effectuer des calculs par quatre processus. Dans ce cas, on devrait essayer de distribuer toutes les opérations arithmétiques vectorielles de manière relativement égale sur les processus. Voici ce que j'ai obtenu:
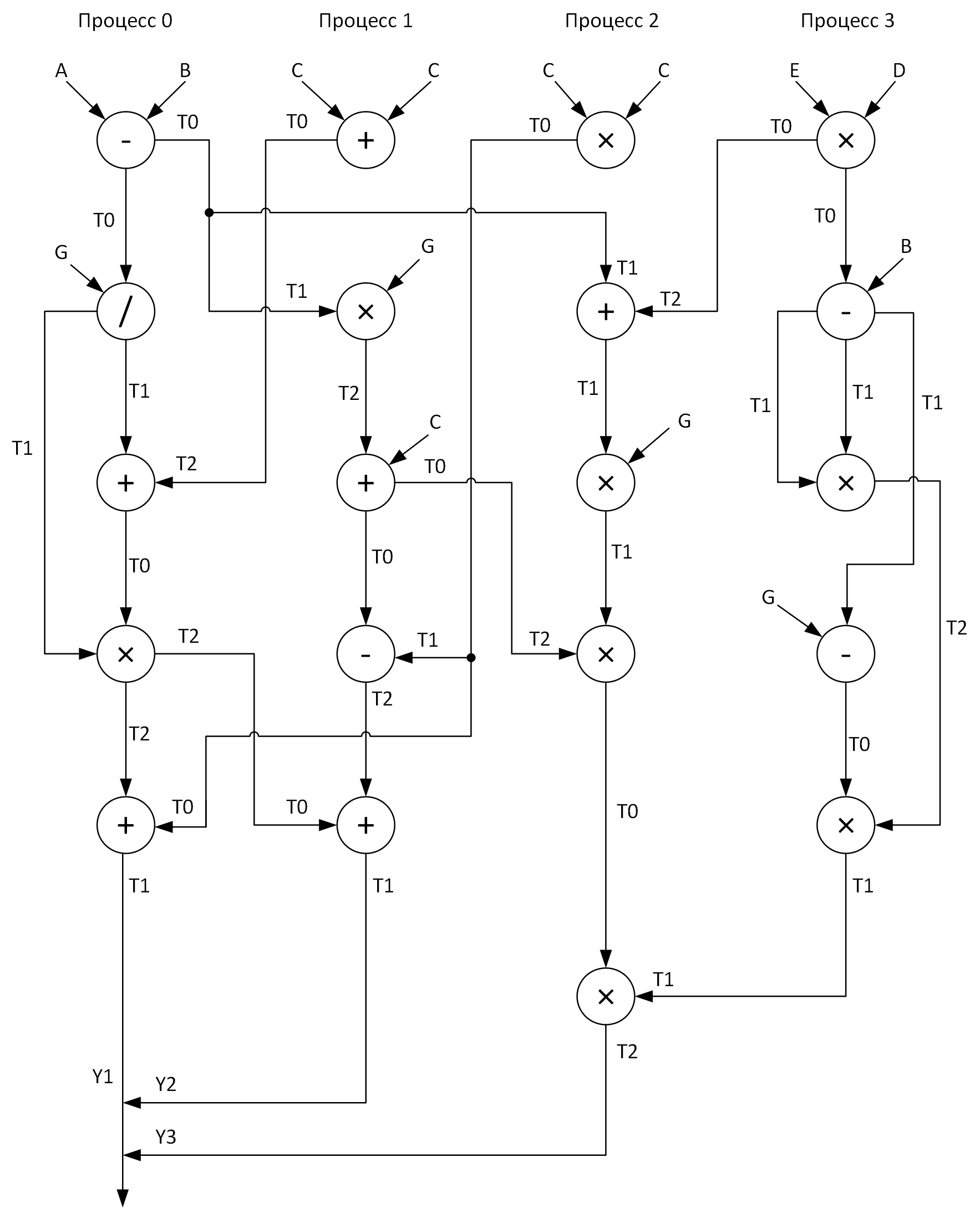
Voir ces tableaux T0-T2? Ce sont des tampons pour stocker les résultats intermédiaires des opérations. De plus, sur un graphique lors de l'envoi de messages d'un processus à un autre, au début de la flèche se trouve le nom du tableau dont les données sont transmises et à la fin de la flèche se trouve le tableau qui reçoit ces données.
Eh bien, quand avons-nous finalement répondu aux questions:
- Quel genre de problème résolvons-nous?
- Quels outils utiliserons-nous pour le résoudre?
- Comment allons-nous le résoudre?
Il ne reste plus qu'à le résoudre ...
Notre «solution:»
Ensuite, je présenterai les codes des deux programmes discutés ci-dessus, mais pour commencer, je donnerai quelques explications supplémentaires sur quoi et comment.
J'ai supprimé toutes les opérations arithmétiques vectorielles dans des procédures distinctes (add, sub, mul, div) afin d'augmenter la lisibilité du code. Tous les tableaux d'entrée sont initialisés conformément aux formules que j'ai indiquées
presque au hasard. Étant donné que le processus zéro recueille les résultats du travail de tous les autres processus, il fonctionne donc le plus longtemps, il est donc logique de considérer le temps de son travail égal à l'exécution du programme (comme nous nous en souvenons, nous sommes intéressés par: arithmétique + messagerie) dans les premier et deuxième cas. Nous mesurerons les intervalles de temps en utilisant la fonction
MPI_Wtime, et en même temps j'ai décidé d'afficher quelle résolution des montres que j'ai là en utilisant
MPI_Wtick (quelque part dans mon âme j'espère qu'elles s'intègrent dans mon TSC invariant, dans ce cas, je suis même prêt à leur pardonner l'erreur associée à l'heure à laquelle la fonction a été appelée MPI_Wtime). Donc, nous allons rassembler tout ce que j'ai écrit ci-dessus et conformément au graphique, nous allons enfin développer ces programmes (et déboguer bien sûr aussi).
Qui se soucie de voir le code:
Programme avec blocage des transferts de données#include "pch.h" #include <iostream> #include <iomanip> #include <fstream> #include <mpi.h> using namespace std; void add(double *A, double *B, double *C, int n); void sub(double *A, double *B, double *C, int n); void mul(double *A, double *B, double *C, int n); void div(double *A, double *B, double *C, int n); int main(int argc, char **argv) { if (argc < 2) { return 1; } int n = atoi(argv[1]); int rank; double start_time, end_time; MPI_Status status; double *A = new double[n]; double *B = new double[n]; double *C = new double[n]; double *D = new double[n]; double *E = new double[n]; double *G = new double[n]; double *T0 = new double[n]; double *T1 = new double[n]; double *T2 = new double[n]; for (int i = 0; i < n; i++) { A[i] = double (2 * i + 1); B[i] = double(2 * i); C[i] = double(0.003 * (i + 1)); D[i] = A[i] * 0.001; E[i] = B[i]; G[i] = C[i]; } cout.setf(ios::fixed); cout << fixed << setprecision(9); MPI_Init(&argc, &argv); MPI_Comm_rank(MPI_COMM_WORLD, &rank); if (rank == 0) { start_time = MPI_Wtime(); sub(A, B, T0, n); MPI_Send(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD); MPI_Send(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD); div(T0, G, T1, n); MPI_Recv(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &status); add(T1, T2, T0, n); mul(T0, T1, T2, n); MPI_Recv(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &status); MPI_Send(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD); add(T0, T2, T1, n); MPI_Recv(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &status); MPI_Recv(T2, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &status); end_time = MPI_Wtime(); cout << "Clock resolution: " << MPI_Wtick() << " secs" << endl; cout << "Thread " << rank << " execution time: " << end_time - start_time << endl; } if (rank == 1) { add(C, C, T0, n); MPI_Recv(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &status); MPI_Send(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD); mul(T1, G, T2, n); add(T2, C, T0, n); MPI_Recv(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &status); MPI_Send(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD); sub(T1, T0, T2, n); MPI_Recv(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &status); add(T0, T2, T1, n); MPI_Send(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD); } if (rank == 2) { mul(C, C, T0, n); MPI_Recv(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &status); MPI_Recv(T2, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &status); MPI_Send(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD); MPI_Send(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD); add(T1, T2, T0, n); mul(T0, G, T1, n); MPI_Recv(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &status); mul(T1, T2, T0, n); MPI_Recv(T1, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &status); mul(T0, T1, T2, n); MPI_Send(T2, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD); } if (rank == 3) { mul(E, D, T0, n); MPI_Send(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD); sub(T0, B, T1, n); mul(T1, T1, T2, n); sub(T1, G, T0, n); mul(T0, T2, T1, n); MPI_Send(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD); } MPI_Finalize(); delete[] A; delete[] B; delete[] C; delete[] D; delete[] E; delete[] G; delete[] T0; delete[] T1; delete[] T2; return 0; } void add(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] + B[i]; } } void sub(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] - B[i]; } } void mul(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] * B[i]; } } void div(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] / B[i]; } }
Programme avec transferts de données non bloquants différés #include "pch.h" #include <iostream> #include <iomanip> #include <fstream> #include <mpi.h> using namespace std; void add(double *A, double *B, double *C, int n); void sub(double *A, double *B, double *C, int n); void mul(double *A, double *B, double *C, int n); void div(double *A, double *B, double *C, int n); int main(int argc, char **argv) { if (argc < 2) { return 1; } int n = atoi(argv[1]); int rank; double start_time, end_time; MPI_Request request[7]; MPI_Status statuses[4]; double *A = new double[n]; double *B = new double[n]; double *C = new double[n]; double *D = new double[n]; double *E = new double[n]; double *G = new double[n]; double *T0 = new double[n]; double *T1 = new double[n]; double *T2 = new double[n]; for (int i = 0; i < n; i++) { A[i] = double(2 * i + 1); B[i] = double(2 * i); C[i] = double(0.003 * (i + 1)); D[i] = A[i] * 0.001; E[i] = B[i]; G[i] = C[i]; } cout.setf(ios::fixed); cout << fixed << setprecision(9); MPI_Init(&argc, &argv); MPI_Comm_rank(MPI_COMM_WORLD, &rank); if (rank == 0) { start_time = MPI_Wtime(); MPI_Send_init(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[0]);// MPI_Send_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[1]);// MPI_Recv_init(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[2]);// MPI_Recv_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[3]);// MPI_Send_init(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[4]);// MPI_Recv_init(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[5]);// MPI_Recv_init(T2, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[6]);// MPI_Start(&request[2]); sub(A, B, T0, n); MPI_Startall(2, &request[0]); div(T0, G, T1, n); MPI_Waitall(3, &request[0], statuses); add(T1, T2, T0, n); mul(T0, T1, T2, n); MPI_Startall(2, &request[3]); MPI_Wait(&request[3], &statuses[0]); add(T0, T2, T1, n); MPI_Startall(2, &request[5]); MPI_Wait(&request[4], &statuses[0]); MPI_Waitall(2, &request[5], statuses); end_time = MPI_Wtime(); cout << "Clock resolution: " << MPI_Wtick() << " secs" << endl; cout << "Thread " << rank << " execution time: " << end_time - start_time << endl; } if (rank == 1) { MPI_Recv_init(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[0]);// MPI_Send_init(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[1]);// MPI_Recv_init(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[2]);// MPI_Send_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[3]);// MPI_Recv_init(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[4]);// MPI_Send_init(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[5]);// MPI_Start(&request[0]); add(C, C, T0, n); MPI_Start(&request[1]); MPI_Wait(&request[0], &statuses[0]); mul(T1, G, T2, n); MPI_Start(&request[2]); MPI_Wait(&request[1], &statuses[0]); add(T2, C, T0, n); MPI_Start(&request[3]); MPI_Wait(&request[2], &statuses[0]); sub(T1, T0, T2, n); MPI_Wait(&request[3], &statuses[0]); MPI_Start(&request[4]); MPI_Wait(&request[4], &statuses[0]); add(T0, T2, T1, n); MPI_Start(&request[5]); MPI_Wait(&request[5], &statuses[0]); } if (rank == 2) { MPI_Recv_init(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[0]);// MPI_Recv_init(T2, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &request[1]);// MPI_Send_init(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[2]);// MPI_Send_init(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[3]);// MPI_Recv_init(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[4]);// MPI_Recv_init(T1, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &request[5]);// MPI_Send_init(T2, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[6]);// MPI_Startall(2, &request[0]); mul(C, C, T0, n); MPI_Startall(2, &request[2]); MPI_Waitall(4, &request[0], statuses); add(T1, T2, T0, n); MPI_Start(&request[4]); mul(T0, G, T1, n); MPI_Wait(&request[4], &statuses[0]); mul(T1, T2, T0, n); MPI_Start(&request[5]); MPI_Wait(&request[5], &statuses[0]); mul(T0, T1, T2, n); MPI_Start(&request[6]); MPI_Wait(&request[6], &statuses[0]); } if (rank == 3) { MPI_Send_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[0]); MPI_Send_init(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[1]); mul(E, D, T0, n); MPI_Start(&request[0]); sub(T0, B, T1, n); mul(T1, T1, T2, n); MPI_Wait(&request[0], &statuses[0]); sub(T1, G, T0, n); mul(T0, T2, T1, n); MPI_Start(&request[1]); MPI_Wait(&request[1], &statuses[0]); } MPI_Finalize(); delete[] A; delete[] B; delete[] C; delete[] D; delete[] E; delete[] G; delete[] T0; delete[] T1; delete[] T2; return 0; } void add(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] + B[i]; } } void sub(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] - B[i]; } } void mul(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] * B[i]; } } void div(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] / B[i]; } }
Test et analyse
Exécutons nos programmes pour des tableaux de différentes tailles et voyons ce qui se passe. Les résultats des tests sont résumés dans le tableau, dans la dernière colonne dont nous calculons et écrivons le coefficient d'accélération, que nous définissons comme suit: K
accele = T
ex. non bloquant. /
Bloc T.
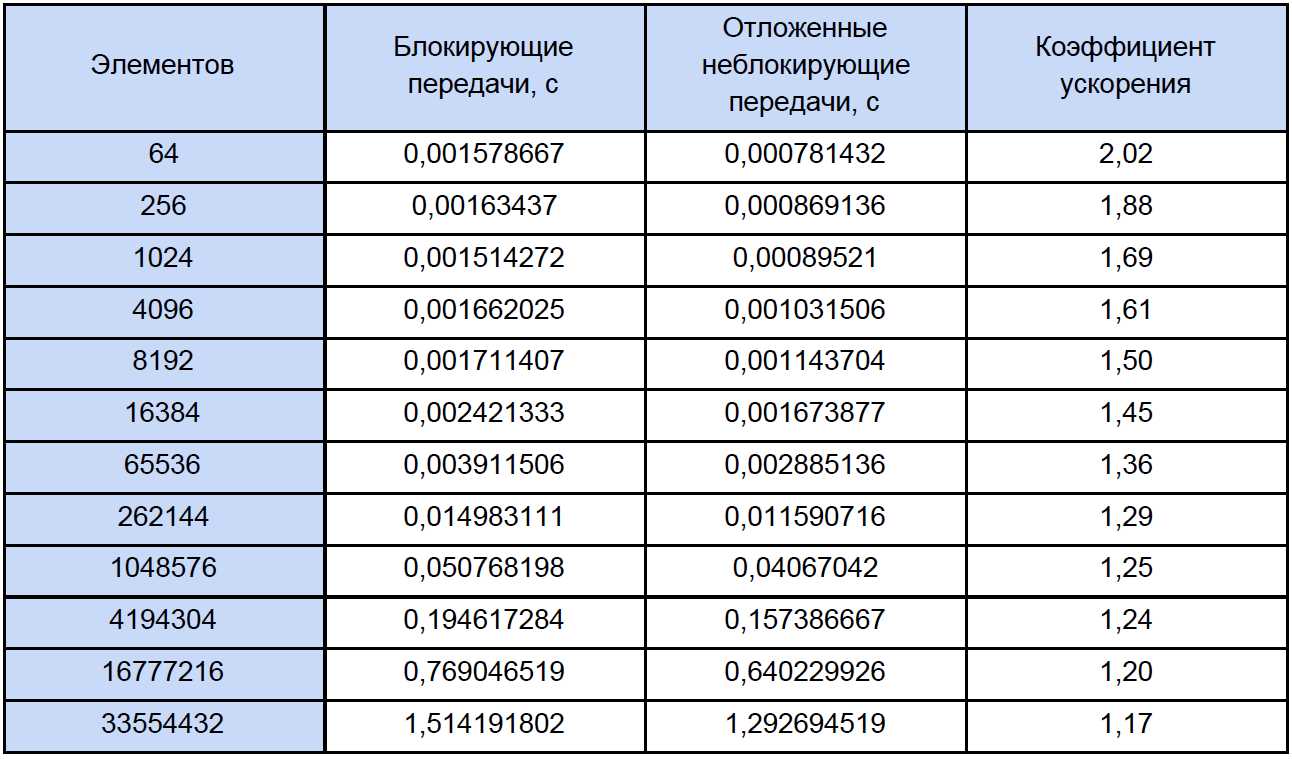
Si vous regardez ce tableau un peu plus attentivement que d'habitude, vous remarquerez qu'avec une augmentation du nombre d'éléments traités, le coefficient d'accélération diminue en quelque sorte comme ceci:

Essayons de déterminer quel est le problème? Pour ce faire, je propose d'écrire un petit programme de test qui mesurera le temps de chaque opération arithmétique vectorielle et réduira soigneusement les résultats dans un fichier texte ordinaire.
Ici, en fait, le programme lui-même:
Mesure du temps #include "pch.h" #include <iostream> #include <iomanip> #include <Windows.h> #include <fstream> using namespace std; void add(double *A, double *B, double *C, int n); void sub(double *A, double *B, double *C, int n); void mul(double *A, double *B, double *C, int n); void div(double *A, double *B, double *C, int n); int main() { struct res { double add; double sub; double mul; double div; }; int i, j, k, n, loop; LARGE_INTEGER start_time, end_time, freq; ofstream fout("test_measuring.txt"); int N[12] = { 64, 256, 1024, 4096, 8192, 16384, 65536, 262144, 1048576, 4194304, 16777216, 33554432 }; SetConsoleOutputCP(1251); cout << " loop: "; cin >> loop; fout << setiosflags(ios::fixed) << setiosflags(ios::right) << setprecision(9); fout << " : " << loop << endl; fout << setw(10) << "\n " << setw(30) << ". (c)" << setw(30) << ". (c)" << setw(30) << ". (c)" << setw(30) << ". (c)" << endl; QueryPerformanceFrequency(&freq); cout << "\n : " << freq.QuadPart << " " << endl; for (k = 0; k < sizeof(N) / sizeof(int); k++) { res output = {}; n = N[k]; double *A = new double[n]; double *B = new double[n]; double *C = new double[n]; for (i = 0; i < n; i++) { A[i] = 2.0 * i; B[i] = 2.0 * i + 1; C[i] = 0; } for (j = 0; j < loop; j++) { QueryPerformanceCounter(&start_time); add(A, B, C, n); QueryPerformanceCounter(&end_time); output.add += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart); QueryPerformanceCounter(&start_time); sub(A, B, C, n); QueryPerformanceCounter(&end_time); output.sub += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart); QueryPerformanceCounter(&start_time); mul(A, B, C, n); QueryPerformanceCounter(&end_time); output.mul += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart); QueryPerformanceCounter(&start_time); div(A, B, C, n); QueryPerformanceCounter(&end_time); output.div += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart); } fout << setw(10) << n << setw(30) << output.add / loop << setw(30) << output.sub / loop << setw(30) << output.mul / loop << setw(30) << output.div / loop << endl; delete[] A; delete[] B; delete[] C; } fout.close(); cout << endl; system("pause"); return 0; } void add(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] + B[i]; } } void sub(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] - B[i]; } } void mul(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] * B[i]; } } void div(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] / B[i]; } }
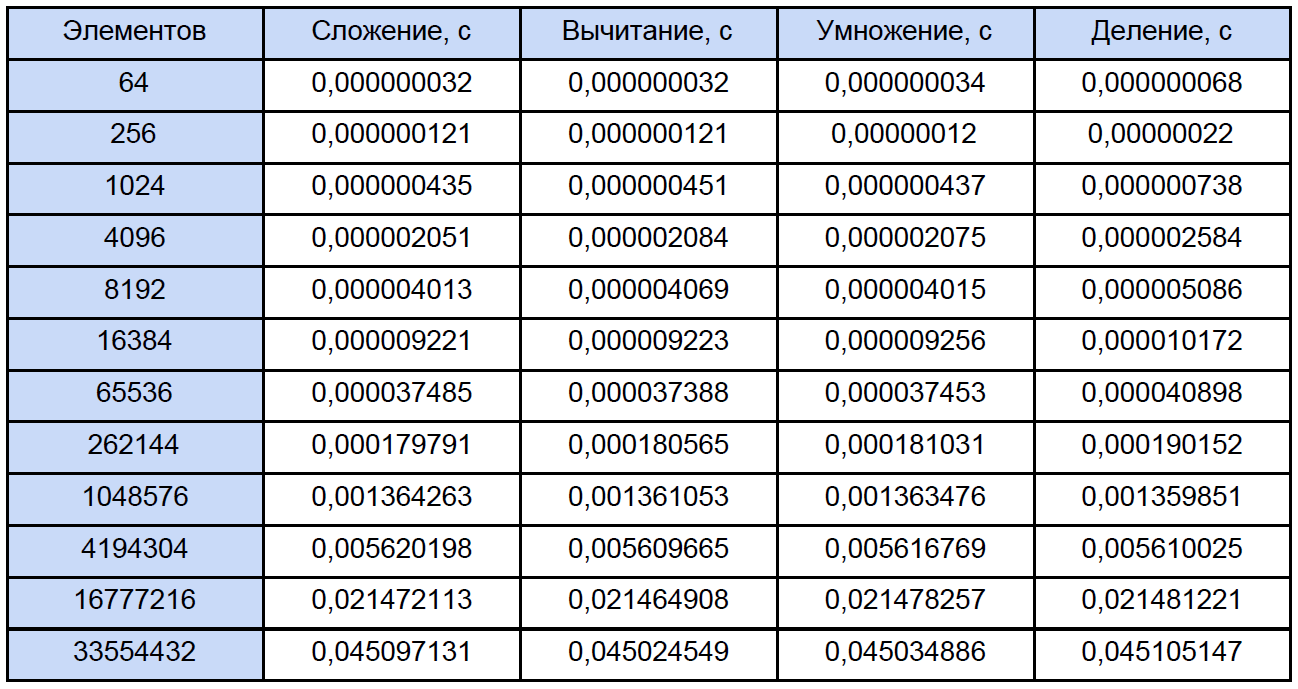
Au démarrage, il vous demande de saisir le nombre de cycles de mesure, j'ai testé 10 000 cycles. En sortie, on obtient le résultat moyen pour chaque opération:
Pour mesurer le temps, j'ai utilisé le
QueryPerformanceCounter de haut niveau. Je recommande fortement de lire
cette FAQ afin que la plupart des questions sur la mesure du temps avec cette fonction disparaissent d'elles-mêmes. Selon mes observations, il s'accroche au TSC (mais théoriquement ce n'est peut-être pas pour lui), mais renvoie, selon l'aide, le nombre actuel de ticks du compteur. Mais le fait est que mon compteur ne peut physiquement pas mesurer l'intervalle de temps de 32 ns (voir la première ligne du tableau des résultats). Ce résultat est dû au fait qu'entre les deux appels du QueryPerformanceCounter, 0 tick ou 1 tick passe. Pour la première ligne du tableau, nous pouvons seulement conclure qu'environ un tiers des 10 000 résultats sont égaux à 1 tick.
Ainsi, les données de ce tableau pour 64, 256 et même pour 1024 éléments sont quelque chose d'assez approximatif. Maintenant, ouvrons l'un des programmes et calculons le nombre total d'opérations de chaque type qu'il rencontre, traditionnellement, nous «répartissons» tout selon le tableau suivant:
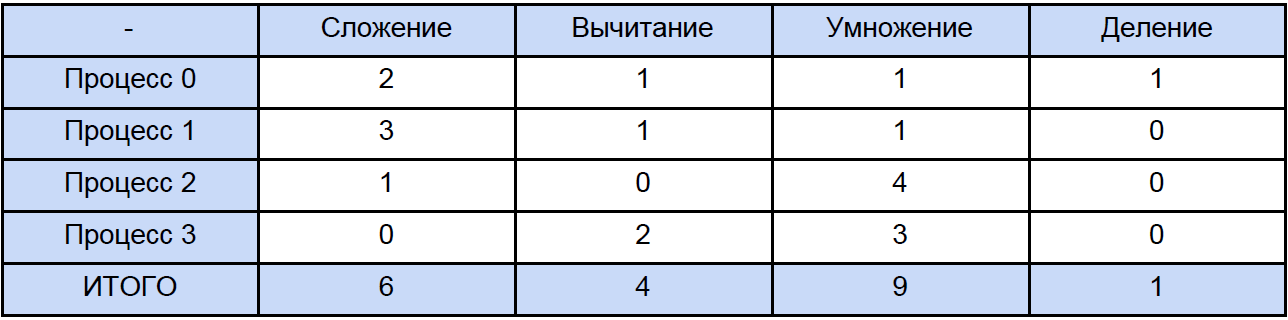
Enfin, nous connaissons le temps de chaque opération arithmétique vectorielle et combien il est dans notre programme, essayons de savoir combien de temps est consacré à ces opérations dans des programmes parallèles et combien de temps est consacré au blocage et à l'échange de données non bloquant différé entre les processus et encore, pour plus de clarté, nous allons le réduire à table:
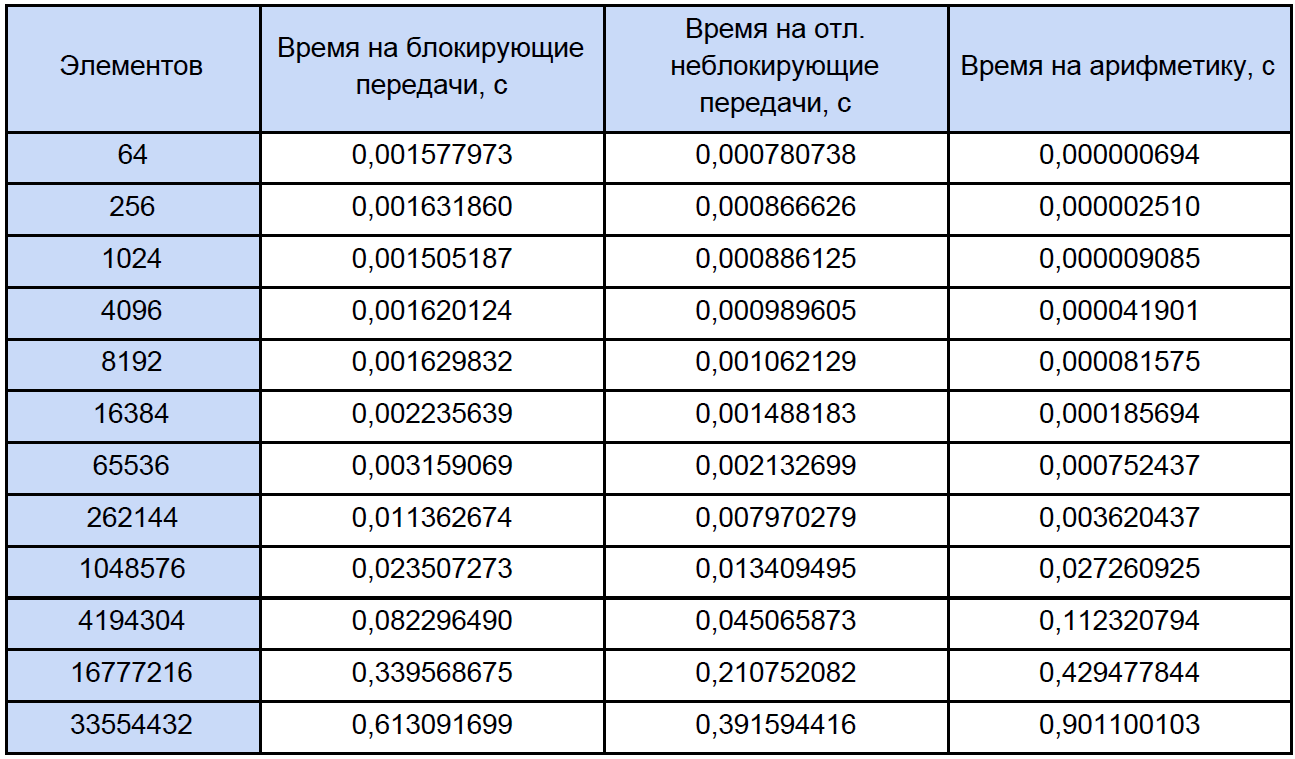
Sur la base des résultats des données obtenues, nous construisons un graphique de trois fonctions: la première décrit le changement du temps passé à bloquer les transferts entre les processus, à partir du nombre d'éléments du tableau, le second décrit le changement du temps passé sur les transferts différés non bloquants entre les processus, sur le nombre d'éléments du tableau et le troisième décrit le changement dans le temps, dépensé en opérations arithmétiques, à partir du nombre d'éléments de tableaux:
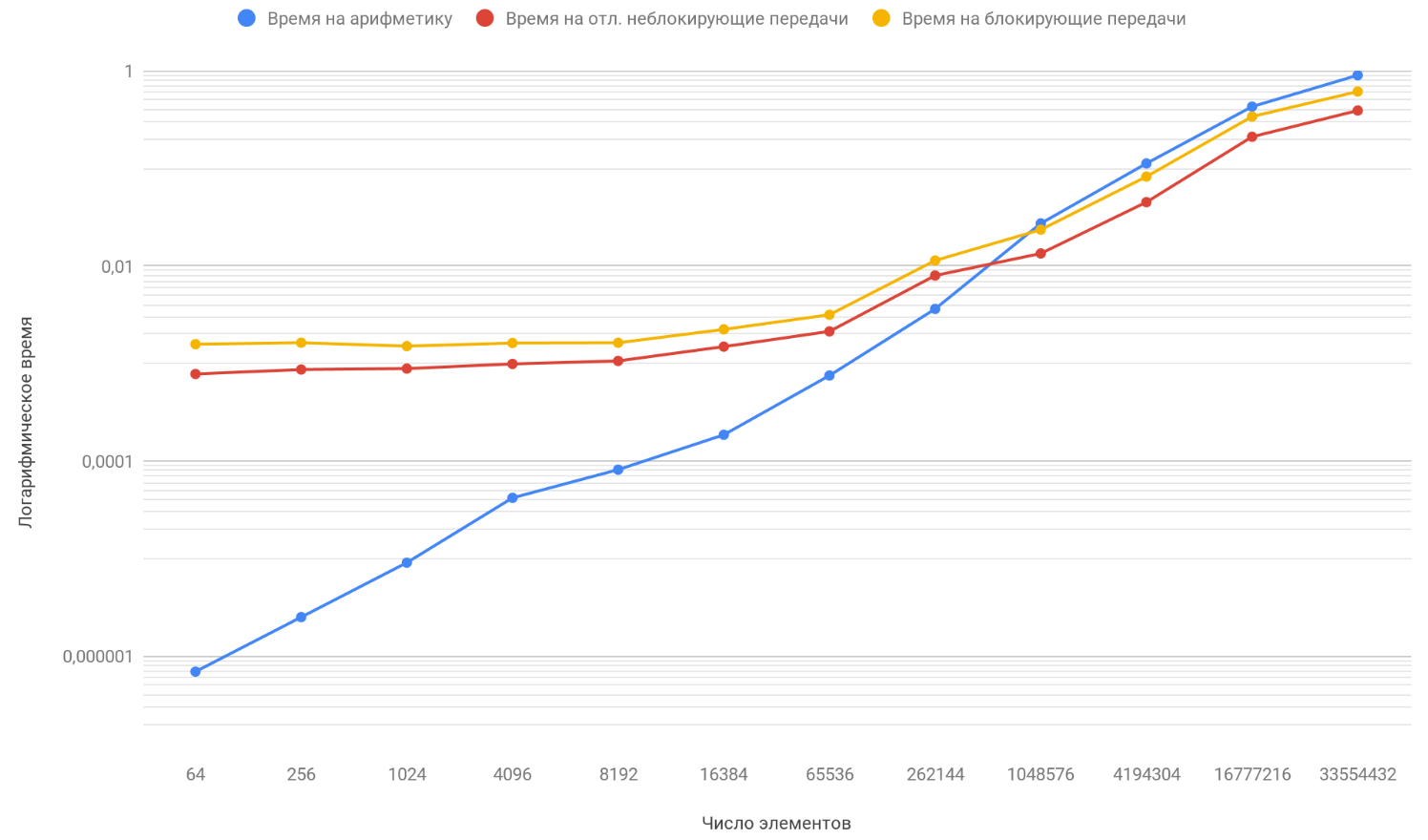
Comme vous l'avez déjà remarqué, l'échelle verticale du graphique est logarithmique, c'est une mesure nécessaire, car la dispersion des temps est trop grande et sur un graphique régulier, rien n'aurait été visible. Faites attention à la fonction de la dépendance du temps passé à l'arithmétique sur le nombre d'éléments, elle dépasse en toute sécurité les deux autres fonctions d'environ 1 million d'éléments. Le truc c'est qu'il croît à l'infini plus vite que ses deux adversaires. Par conséquent, avec une augmentation du nombre d'éléments traités, l'exécution des programmes est de plus en plus déterminée par l'arithmétique plutôt que par les transferts. Supposons que vous augmentiez le nombre de transferts entre les processus, conceptuellement, vous ne verrez que le moment où la fonction arithmétique dépassera les deux autres se produira plus tard.
Résumé
Ainsi, en continuant d'augmenter la longueur des tableaux, vous arriverez à la conclusion qu'un programme avec des transferts non bloquants différés ne sera que très légèrement plus rapide que celui qui utilise l'échange bloquant. Et si vous dirigez la longueur des tableaux vers l'infini (enfin, ou prenez simplement des tableaux très longs), la durée de fonctionnement de votre programme sera déterminée à 100% par des calculs, et le coefficient d'accélération tendra en toute sécurité à 1.