En mars 2016, Robert J. Lemke-Oliver et Kannan Sundararajan de l'Université de Stanford ont
ouvert un nouveau modèle dans la distribution des nombres premiers. Il s'est avéré que les nombres premiers sont
spécifiquement distribués sur l'espace numérique. Pour plus de détails voir la traduction de l'article
«Structure et aléatoire des nombres premiers» sur Habré.
Des experts d'autres domaines, dont la chimie, se sont joints à l'étude du sujet. Et avec succès. Le professeur de chimie théorique
Salvatore Torcuato, ainsi que le théoricien des nombres
Matthew de Courcy-Ireland, ont trouvé de
nouveaux modèles dans la distribution des nombres premiers qui n'étaient pas connus auparavant. Il s'est avéré que la distribution des nombres premiers forme un modèle de diffraction de type fractal, quelque peu similaire au modèle de diffraction des quasi-cristaux exotiques.
Le professeur Torcuato est spécialisé dans l'étude des modèles dans les structures des systèmes physiques, tels que les cristaux et les colloïdes. La méthode standard pour étudier la structure est la diffraction des rayons X. Des molécules aléatoires dans des liquides ou des gaz réfléchissent les rayons dans toutes les directions sans créer de motif notable. Mais les atomes situés symétriquement dans un cristal réfléchissent de manière synchrone les ondes lumineuses, créant des taches lumineuses périodiques de diffraction prononcée (
pics de Bragg ). Une analyse des pics de Bragg permet de comprendre la structure interne d'un cristal ou d'un autre matériau qui crée une telle image.
Ainsi, dans de nouveaux articles scientifiques de Torkuato et d'autres (
1 ,
2 ,
3 ), il est montré que la structure ordonnée découverte dans la distribution des nombres premiers n'est rien de plus qu'un modèle de diffraction de type fractal, similaire à celui des quasi-cristaux.
L'image des pics de Bragg sur un réseau de nombres premiers est similaire aux quasi-cristaux, mais en diffère toujours. Torcuato
dit que les nombres premiers en tant que système physique "sont une catégorie complètement nouvelle de structures". Les chercheurs ont appelé ce nouveau modèle de type fractal «périodicité limite efficace».
La figure se compose d'une séquence périodique de pics brillants qui reflètent les intervalles premiers les plus courants: ils sont tous impairs (à l'exception de 2), plusieurs côte à côte. Les pics les plus brillants (paires séparées par deux chiffres) alternent à intervalles réguliers avec des pics moins brillants, reflétant des nombres premiers séparés par six chiffres. Entre eux se trouvent même des pics plus faibles correspondant à des paires de nombres premiers plus éloignés, etc. Tout cela est un nombre infini de pics de Bragg placés les uns dans les autres.
Une structure similaire des pics de Bragg a été observée plus tôt - dans les profils de diffraction des quasi-cristaux.
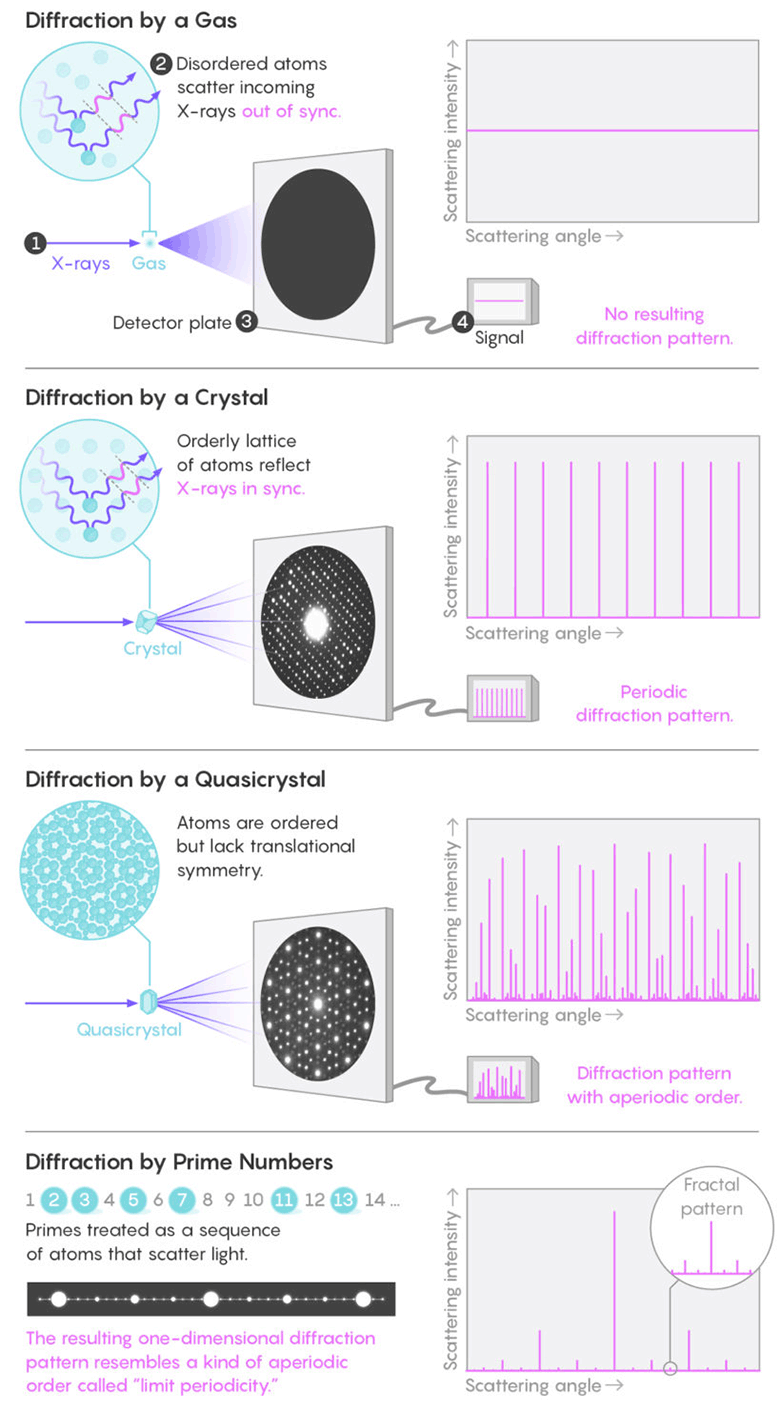Des molécules aléatoires dans des liquides ou des gaz réfléchissent les rayons dans toutes les directions sans créer de motif notable. Mais les atomes situés symétriquement dans un cristal réfléchissent de manière synchrone les ondes lumineuses, créant des taches lumineuses périodiques de diffraction prononcée. Il s'est avéré que le modèle de distribution des nombres premiers forme un modèle de diffraction fractale, similaire à celui des quasi-cristauxLes quasi -
cristaux sont des matériaux étranges découverts dans les années 1980. Ils se caractérisent par une symétrie interdite en cristallographie classique et la présence d'ordre à longue portée. Les mosaïques apériodiques du type de la célèbre
mosaïque de Penrose sont un modèle mathématique de quasi-cristaux. Dans ces mosaïques, la symétrie translationnelle est absente, la répétabilité et la quasi-cristallinité sont présentes (symétrie du cinquième ordre).
Fragment de mosaïque de Penrose type P1 (à partir de carreaux de six types)Dans le cas des nombres premiers, les distances entre les pics sont proportionnelles les unes aux autres, contrairement aux pics de Bragg irrationnellement espacés des quasi-cristaux. "Les nombres premiers impliquent en fait un état complètement différent de la position des particules, semblable aux quasi-cristaux mais pas comme les quasi-cristaux", a
déclaré Torcuato.
La découverte du motif de diffraction ne peut pas être qualifiée de découverte révolutionnaire pour la théorie des nombres, car la majeure partie de ces motifs a déjà été décrite précédemment, uniquement par d'autres méthodes mathématiques (pas par diffraction de quasi-cristaux). Ainsi, en utilisant le modèle de diffraction, il est possible de prédire des "doubles" des types 17 et 19 - c'est l'équivalent mathématique de la
première hypothèse de Hardy-Littlewood concernant l'existence de tuples de nombres premiers sur un segment donné de la droite numérique. L'une des règles interdit les triplets de nombres impairs consécutifs après {3, 5, 7}. Cela explique également pourquoi le prochain pic de Bragg le plus brillant du diagramme de diffraction correspond à des nombres séparés par six chiffres plutôt que quatre.
Un nouveau travail scientifique n'est qu'un regard neuf sur le problème de la distribution uniforme des nombres premiers et un moyen plus facile de dériver une certaine «loi unique» pour eux. De plus, il s'agit d'une façon inhabituelle d'analyser un problème mathématique du point de vue de la cristallographie, notamment du point de vue d'un domaine de recherche relativement jeune appelé «ordre apériodique», qui étudie des modèles non répétitifs et se situe à l'intersection de la cristallographie, des systèmes dynamiques, de l'analyse harmonique et de la géométrie discrète. Cette branche de la science s'est développée après la découverte des quasi-cristaux, quand il est devenu clair que les anciennes méthodes ne fonctionnaient pas ici.
La distribution des nombres premiers ressemble à un ordre apériodique spécial, connu depuis les années 1950. C'est ce qu'on appelle la périodicité limite. Dans de tels systèmes, les intervalles périodiques sont imbriqués dans une hiérarchie infinie, de sorte que dans n'importe quel intervalle, le système contient des parties de motifs qui ne sont répétées que dans un intervalle plus grand, comme dans la tuile Taylor-Sokolar.
Carreau Taylor-SokolarLes calculs théoriques montrent que les phases périodiques maximales d'une substance devraient pouvoir se former dans la nature, et de tels systèmes peuvent avoir des propriétés inhabituelles. Mais personne n'a deviné de relier la périodicité limite aux nombres premiers. Nous savons maintenant qu'il existe une telle connexion, et les nombres premiers démontrent un nouveau type de périodicité limite - la périodicité limite «effective», car le synchronisme dans les distances entre les nombres premiers dans tout le système n'est observé que statistiquement.
La question se pose: comment les modèles de distribution des nombres premiers peuvent-ils affecter la force des algorithmes cryptographiques?
«Je reçois vraiment beaucoup de lettres à ce sujet. Bien qu'il s'agisse d'une étude intéressante, elle n'a rien à voir avec la cryptographie », a
écrit le célèbre cryptographe Bruce Schneier sur son blog. - Les cryptographes ne sont pas intéressés à trouver des nombres premiers ni même leur distribution. La persistance d'algorithmes de cryptographie à clé publique de type RSA est associée à la difficulté de factoriser de grands nombres composites, qui sont le produit de nombres premiers. Et c'est une tout autre affaire. »
Ainsi, malgré les progrès dans l'étude de la distribution des nombres premiers, il n'y a pas encore lieu de s'inquiéter de la force des codes cryptographiques.
