Problèmes d'écriture moderne de textes mathématiques

Dans un article récent, le camarade KvanTTT a soulevé la question :

Pouvez-vous expliquer ce que vous n'aimez pas dans les formules modernes (énoncés mathématiques et) et comment peut-il être amélioré?

J'ai essayé de répondre dans un commentaire, mais la taille du champ de texte ne m'a pas permis de terminer les calculs. Cet article est une réponse trop détaillée.

Je dois dire que le matériel est holivarny. En partie trop émotif. Très controversé. Trop personnel - souvent basé sur une expérience personnelle, pas riche, bien que diversifié. Le poste concerne les manuels scolaires et universitaires: la littérature «professionnelle» a ses spécificités, son public . Il n'y a pas de solution au problème dans les réalités actuelles. Dans le même temps, certaines de mes observations bien avant moi ont été exprimées par des autorités telles que Knut et Hamming; les gars un peu moins populaires ont même lavé l'instruction " Comment lire les mathématiques ".

Donc, à mon avis, le principal grief n'est pas tant de rédiger des formules que de présenter du matériel . De plus, à la présentation de matériel à presque tous les niveaux d'enseignement, à partir de l'école et se terminant par les sciences avancées. Le début de la situation actuelle a été posé par Euclide, qui a déclaré l'absence de la voie royale en mathématiques. La route royale n'a pas été pavée jusqu'à présent. Euclide l'a fait, et nous le pouvons.

Le premier problème est que la signification n'est pas montrée . Un autre cadeau d'Euclid: "Donnez un centime au questionneur s'il recherche des avantages, pas des mathématiques." Les auteurs commencent à introduire des définitions, à prouver des théorèmes et à faire d'autres calculs sans expliquer pourquoi cela est nécessaire. Exemple: un manuel sur l'analyse mathématique de Fichtenholtz . Lisez le premier chapitre: «du cours de l'école, vous connaissez les nombres rationnels, mais les besoins des mathématiques nous obligent à introduire des nombres réels ...» et cela a commencé. Quels sont les besoins, quel type de mathématiques, pourquoi le rationnel n'est-il pas heureux - oui, le chien le connaît. "Évidemment."

Ou un autre exemple du même tutoriel. "Le nombre constant a est appelé la limite des options $$ si pour chaque positif $$ peu importe sa taille, il existe un nombre N tel que toutes les valeurs $$ pour lequel le nombre n> N satisfait l'égalité $$ . "

La plupart des élèves ne comprennent pas la définition ci-dessus, mais après six mois, ils s'y habituent. Encore plus d'étudiants, même vers la fin de leurs études, ne savent pas pourquoi ils avaient besoin du concept de limite de séquence. De même pour les fonctions, les intégrales, les séries ... Fichtenholtz décrit certains objets mathématiques, donne parfois des exemples particuliers - et c'est tout. Eh bien, oui, maintenant je comprends que les limites sont nécessaires, par exemple, pour la description correcte des sommes supérieures / inférieures lors de l'introduction des intégrales, mais avant les intégrales, deux semestres de plus!

Ou un déterminant défini comme une fonction multilinéaire asymétrique. Les gars, vous êtes sérieux? La seule réponse adéquate d'un étudiant de première année à une telle définition de «alors quoi»? Quel est l'avantage de cette définition? Je ne discute pas, il y a un avantage, mais est-ce qu'un étudiant de première année peut en être conscient?

Fausse solution au problème : arrière-plan. Il apparaît dans toutes sortes de conférences. "Le problème a été posé par Jacob, examiné par son disciple Abel, et le disciple du disciple Caïn, et cent cinq cents incarnations de Vishnu." Quelle est l'essence du problème, pourquoi il a été résolu par l'auteur original, pourquoi il est si important de tuer des heures de professeur dessus - est omis.

Le prochain problème - les auteurs ne posent pas de vrais problèmes

En principe, il est similaire au précédent. Rappelez-vous le cours de la théorie des probabilités. Quelles tâches y prévalent? "Il y a 25 boules noires et 10 blanches dans le panier ..." Exemples de casino, carte, D&D, économique - non, pas entendu. Nous utiliserons les exemples les plus politiquement corrects, bien que la théorie des probabilités soit issue de la recherche sur les dés.

À propos d'exemples en direct récemment écrit Free_Mic_RS


Les mathématiques commencent par une tâche. Et les tâches mortes et unilatérales donnent l'impression que le théoricien ne fonctionne qu'avec elles. L'intention des auteurs est bonne: donner un exemple, puis passer au général. Résumé de l'exemple. Mais quelques exemples «vivants» rendraient la transition vers l'abstraction beaucoup plus utile. Au moins, je crois fermement que le processus inverse (la transition de l'abstrait au particulier) serait beaucoup plus facile.

Problème: brièveté excessive et incohérence

Tu te souviens de l'école? Et la formule discriminante? Et comment est-il prouvé / dérivé? Une façon: purement algébrique . Nous prenons l'équation $$ , "Multipliez chaque partie par $$ et ajouter $$ "( Pourquoi précisément ces valeurs? ), Encore quelques transformations - et vous avez terminé. Après discriminant, les élèves reçoivent discriminant-pour-même-b. Et puis les formules Vieta. Et aussi des carrés pleins. Et un tas d'exemples. Et loin d'expliquer toujours pourquoi toutes ces méthodes sont nécessaires.

Imaginez maintenant la situation, l’élève se dit: «aujourd’hui, nous allons apprendre à résoudre des équations avec $$ . Tout. " Et une série d'exemples commence par une complication.

$$

Un grand nombre d'exemples qui mènent organiquement à la solution de l'équation à travers des carrés pleins. Ensuite, vous pouvez entrer le discriminant (comme un algorithme simple pour résoudre les équations lorsque les élèves se fatiguent de mettre en surbrillance les carrés pleins), et Viet avec un discriminant pair comme «savoir-faire».

Une approche similaire est utilisée dans les manuels. Hélas, pas du tout. Et pas partout une séquence claire est visible. Selon des rumeurs, certains auteurs ont perdu des feuilles de brouillon dans les tramways, puis ont remplacé les pièces perdues par des expressions comme «il est facile de montrer cela ...». En conséquence, au lieu de sauter calmement d'exemple en exemple, les élèves ont été forcés de sauter par-dessus l'abîme. Combien de personnes se sont cassées et se cassent encore pendant 10 + 6 ans de scolarité / université?

Exemple personnel (demandé dans le message d'origine). Dans la première année de matan, j'ai souffert. En résolvant tranquillement les exemples, il n'a pas du tout appris la théorie. J'ai demandé à un camarade de classe de l'aider à calculer la longueur de la courbe à travers l'intégrale. Il a pris une bouteille de bière, a tracé une courbe aléatoire, l'a redressée avec des segments infiniment petits, a sélectionné un de ces segments, l'a construite jusqu'au triangle dl, dx, dy et a demandé: "Vous souvenez-vous du théorème de Pythagore"? Ensuite, tout était simple.



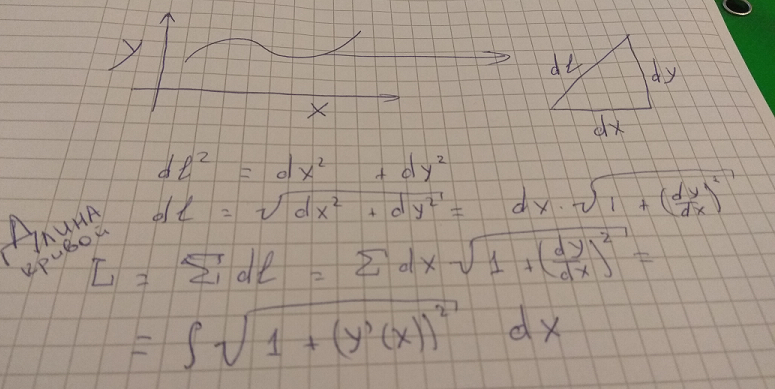
Je lui ai demandé: pourquoi cela n'apparaît-il pas par paires / dans les manuels? Il a montré quelques contre-exemples, a expliqué pourquoi le formalisme est nécessaire chez Matan - et je me suis enlisé. Je viens de lire le théorème, de souligner l'essentiel, d'écrire / résoudre des exemples triviaux, puis de m'occuper du formalisme - et de vraiment comprendre ce qui se passait.

Je ne sais pas s'il est possible d'utiliser massivement l'approche de l' aperçu général => contre-exemples => formalisme . Je ne sais pas combien et quelle théorie / pratique un étudiant a besoin d'acquérir avant la «percée», je peux difficilement imaginer comment mettre des expériences pédagogiques sur ce sujet, et combien de travail je devrai investir dans la recherche. Mais le souvenir de cette explication existe depuis 10 ans. Et après toutes ces années, j'essaie d'abord de donner au public une vue d'ensemble, puis de montrer les problèmes, puis de plonger dans les détails.

Vous direz que mes sentiments personnels peuvent être faux. En plus d'eux, je n'ai que des idées similaires de Hamming :

... Je pouvais étudier quelles méthodes étaient efficaces et lesquelles ne l'étaient pas. Lorsque j'assistais à des réunions, j'ai déjà étudié pourquoi certains travaux sont mémorisés, et la plupart ne le sont pas. Un technicien souhaite donner une conférence technique très limitée. En règle générale, le public souhaite une large conférence de nature générale et souhaite un aperçu et des introductions beaucoup plus généraux que le conférencier ne souhaite en donner. En conséquence, de nombreuses conférences sont inefficaces. Le conférencier appelle le sujet et plonge soudain dans les détails. Peu de gens peuvent suivre. Vous devez dessiner une grande image pour dire pourquoi cela est important, puis déplier lentement un croquis de ce qui a été fait. Ensuite, plus de gens diront: «Oui, Joe l'a fait» ou «Mary a fait ce que je vois vraiment de quoi il s'agit. Oui, Mary a donné une très bonne conférence, je comprends ce qu'elle a fait. " En règle générale, les gens donnent une conférence très limitée et sûre; il est généralement inefficace. De plus, de nombreuses conférences sont remplies d'informations ...

Idées en vrac

Je dois dire que mon expérience dans l'enseignement est extrêmement limitée. Vous avez peut-être remarqué que je me suis limité au programme scolaire et au matanaliz. Hélas, ce sont des domaines où j'ai eu l'occasion de mettre la théorie en contact avec la pratique. Je ne comprends toujours pas l'essence du déterminant en algèbre, je ne réalise pas la géométrie projective, et il y a seulement six mois, j'ai commencé à pénétrer les matrices (juste après l'entraînement, hein). Une bonne illustration du dicton «la théorie sans la pratique est morte».

Comme on m'a dit, dans NMU un nouveau concept a toujours été introduit avec une douzaine de questions. Et si oui? Et si cette clause n'est pas remplie? De quoi a-t-on besoin pour compléter notre concept en semi-groupe? Les auditeurs ont été autorisés à jouer avec le sujet. Habituez-vous. Je pense qu'il vaut la peine de réfléchir attentivement à l'expérience de la NMU.

Certes, dans les branches supérieures des mathématiques, l'approche «d'abord un exemple, puis une abstraction» ne fonctionnera pas. Ainsi, des exemples sur un morceau de papier n'aident pas à réaliser RSA. Mais la durée croissante du programme avec l'augmentation de la longueur des touches permet de ressentir les aspects purement pratiques.

On craint que les manuels scolaires «idéaux / à effet de serre» provoquent un choc lors de l'utilisation de la «tour». Il semble que «un travailleur inconditionnel doit être éduqué dès son jeune âge».

Il est assez difficile de développer des cours, en espérant que les étudiants savent déjà quelque chose. Plus la base requise est grande, plus il est probable que quelque chose de la base soit mal compris par l'étudiant.

Ils disent que le sommet de la forme des mathématiciens a 30 ans. Après 30 ans, vous pouvez déjà les charger pour écrire des manuels, en donnant à un partenaire un méthodologiste spécialisé.

La technologie actuelle vous permet d'écrire des textes en utilisant git. Un article sur la compilation de TeXa en pdf dans le processus CI a récemment glissé sur un hub Je suis sûr qu'une équipe d'auteurs avec de bons outils peut écrire de bien meilleurs manuels.

En plus des professeurs, des enseignants, des étudiants et des écoliers, il y a des états en mathématiques. Et les règlements. Et les exigences. Et la certification. Tout cela affecte les manuels, les auteurs, les enseignants et la qualité du matériel.

Comment améliorer le flux de matière dans les textes mathématiques

Dans les réalités actuelles (russes) - rien. Il y a des passionnés, il y a des professionnels, pas de motivation.

Les professeurs de mathématiques ont assez de leurs tâches pour écrire des manuels. Parfois, les compétences purement humanitaires sont insuffisantes; les livres ne sont pas enseignés dans les universités. De plus, la déformation professionnelle: «l'évidence» pour un professeur peut être écrasante pour les étudiants. Les professeurs de mathématiques sont occupés. Et des papiers. Et le tutorat. Je ne dirai rien de l'Etat. Presque n'a pas rencontré ses représentants, donc il n'y a rien à dire. Sauf si je mentionne la politique de remplacement des manuels tous les trois ans. Après l'école, je voulais emmener mes manuels à la bibliothèque, ils m'ont dit "ils sont vieux, tu ne peux pas les garder". La motivation pour écrire de bons manuels n'ajoute pas cette approche.

En d'autres termes, je ne m'attends pas personnellement à des progrès positifs de la part du système éducatif. J'espère bien sûr, mais je n'attends pas. Ce qui nous aide, ce sont des aperçus de l'informatique et d'autres techniques. Lors d'une des conférences mathématiques, j'ai reçu un livre sur l'infographie d'un des participants. L'auteur travaillait dans un bureau développant un noyau graphique d'un système de dessin, et le matériel était assez bon. Les mathématiques n'étaient pas «pures», appliquées, mais le fait de l'existence d'un bon matériel éducatif était certainement agréable.

Autre approche: les enseignants des entreprises travaillant dans les universités. On ne peut pas s'attendre à des textes mathématiques de ces gars, les détails ne sont pas les mêmes. À moins que les développeurs de jeux n'écrivent un manuel sur la théorie, ou que les graphiques n'écrivent sur l'algèbre / la géométrie nécessaire pour développer les mêmes systèmes de CAO (s'il existe de tels projets - appelez) .

Enfin, il existe différentes plateformes éducatives non étatiques, comme la même Coursera. Ces gars-là peuvent tout faire, car ils travaillent pour de l'argent, rivalisent et reçoivent rapidement des commentaires. Mais ils ont leur propre inconvénient: le format de soumission des données est différent. Ils n’écrivent pas de textes directement.

Et qu'est-ce qui va venir dans le futur?

Le plus intéressant. Peut-être que tout restera tel quel. Peut-être qu'il y aura un écart par rapport aux textes en mathématiques. Ou peut-être que les auteurs seront inspirés par l’idée «le texte du produit doit être pratique pour le client du lecteur », et les pionniers pourront briser la tradition. Ensuite, dans 30-50-100 ans, nous aurons des manuels compréhensibles pour la plupart des lecteurs.

Upd1. J'ai inséré une photo avec le calcul de la longueur de la section de courbe.

Upd2. Dans les commentaires, il est souvent mentionné que le texte est consacré aux problèmes de l'enseignement et non aux mathématiques professionnelles. La raison est simple: la plupart des travaux «professionnels» que j'ai vus en termes de présentation de matériel ne diffèrent pas des manuels. Dans le même temps, la littérature scolaire / universitaire est connue de la majorité des habr et «professionnelle» pour cent.