Caractéristiques du filtrage des fenêtres sur FPGA

Bonjour à tous! Cet article se concentrera sur une partie importante du traitement numérique du signal - le filtrage du signal de fenêtre, en particulier sur les FPGA. L'article montrera comment concevoir des fenêtres classiques de longueur standard et des fenêtres "longues" de 64K à 16M + échantillons. Le langage de développement principal est le VHDL, la base de l'élément est les derniers cristaux FPGA Xilinx des dernières familles: ce sont Ultrascale, Ultrascale +, 7-series. L'article montrera l'implémentation de CORDIC - le noyau de base pour configurer les fonctions de fenêtre de n'importe quelle durée, ainsi que les fonctions de fenêtre de base. L'article décrit la méthode de conception utilisant des langages de haut niveau C / C ++ dans Vivado HLS. Comme d'habitude, à la fin de l'article, vous trouverez un lien vers les codes sources du projet.

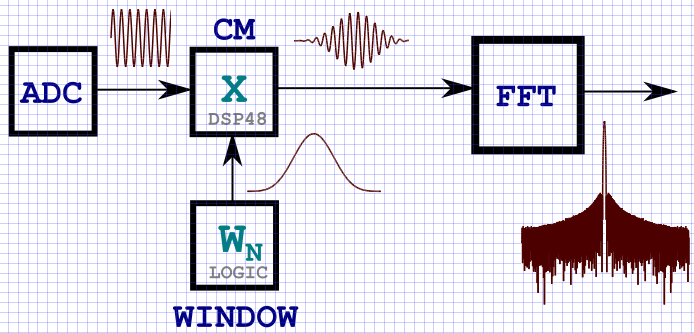
KDPV: un schéma typique de transmission de signal via des nœuds DSP pour des tâches d'analyse de spectre.

Présentation

Grâce au cours «Traitement numérique du signal», de nombreuses personnes savent que pour une forme d'onde sinusoïdale infinie dans le temps, son spectre est une fonction delta à la fréquence du signal. En pratique, le spectre d'un signal harmonique limité dans le temps réel est équivalent à la fonction ~ sin (x) / x , et la largeur du lobe principal dépend de la durée de l'intervalle d'analyse du signal T. La limite de temps n'est rien d'autre que la multiplication du signal par une enveloppe rectangulaire. Il est connu du cours DSP que la multiplication des signaux dans le domaine temporel est une convolution de leurs spectres dans le domaine fréquentiel (et vice versa), par conséquent, le spectre de l'enveloppe rectangulaire limitée du signal harmonique est équivalent à ~ sinc (x). Cela est également dû au fait que nous ne pouvons pas intégrer le signal sur un intervalle de temps infini, et la transformée de Fourier sous forme discrète, exprimée par une somme finie, est limitée par le nombre d'échantillons. En règle générale, la longueur de la FFT dans les appareils de traitement numérique FPGA modernes prend des valeurs NFFT de 8 à plusieurs millions de points. En d'autres termes, le spectre du signal d'entrée est calculé sur l'intervalle T , qui dans de nombreux cas est égal à NFFT . En limitant le signal à l'intervalle T , on impose ainsi une «fenêtre» rectangulaire d'une durée de T échantillons. Par conséquent, le spectre résultant est le spectre du signal harmonique multiplié et de l'enveloppe rectangulaire. Dans les tâches DSP, des fenêtres de formes diverses ont été inventées depuis longtemps, qui, superposées à un signal dans le domaine temporel, peuvent améliorer ses caractéristiques spectrales. Un grand nombre de fenêtres différentes est principalement dû à l'une des principales caractéristiques de toute superposition de fenêtres. Cette caractéristique s'exprime dans la relation entre le niveau des lobes latéraux et la largeur du lobe central. Un schéma bien connu: plus la suppression des lobes latéraux est forte, plus le lobe principal est large et vice versa.

L'une des applications des fonctions de fenêtre: détection de signaux faibles sur fond de plus forts en supprimant le niveau des lobes latéraux. Les principales fonctions de la fenêtre dans les tâches DSP sont une fenêtre triangulaire, sinusoïdale, Lanczos, Hann, Hamming, Blackman, Harris, Blackman-Harris, une fenêtre à toit plat, Natall, Gauss, une fenêtre Kaiser et bien d'autres. La plupart d'entre eux sont exprimés à travers une série finie en additionnant des signaux harmoniques avec des poids spécifiques. Les fenêtres de forme complexe sont calculées en prenant un exposant (fenêtre gaussienne) ou une fonction de Bessel modifiée (fenêtre de Kaiser), et ne seront pas prises en compte dans cet article. Vous pouvez en savoir plus sur les fonctions des fenêtres dans la littérature, que je donnerai traditionnellement à la fin de l'article.

La figure suivante montre les fonctions de fenêtre typiques et leurs caractéristiques spectrales construites à l'aide des outils de CAO Matlab.

Implémentation

Au début de l'article, j'ai inséré KDPV, qui montre en termes généraux un diagramme structurel de la multiplication des données d'entrée par une fonction de fenêtre. De toute évidence, la façon la plus simple d'implémenter le stockage d'une fonction de fenêtre dans le FPGA est de l'écrire en mémoire (bloc RAMB ou distribué distribué - cela n'a pas beaucoup d'importance), puis de récupérer cycliquement les données lorsque les échantillons d'entrée du signal arrivent. En règle générale, dans les FPGA modernes, la quantité de mémoire interne permet de stocker des fonctions de fenêtre de tailles relativement petites, qui sont ensuite multipliées par les signaux d'entrée entrants. Par petite, je veux dire des fonctions de fenêtre jusqu'à 64 Ko d'échantillons.

Mais que faire si la fonction de fenêtre est trop longue? Par exemple, 1M de lectures. Il est facile de calculer que pour une telle fonction de fenêtre présentée dans une grille de bits 32 bits, NRAMB = 1024 * 1024 * 32/32768 = 1024 cellules de mémoire de bloc des cristaux FPGA Xilinx de type RAMB36K sont nécessaires. Et pour 16 millions d'échantillons? 16 mille cellules mémoire! Pas un seul FPGA moderne n'a autant de mémoire. Pour de nombreux FPGA, c'est trop, et dans d'autres cas, c'est une utilisation inutile des ressources FPGA (et, bien sûr, de l'argent du client).

À cet égard, vous devez trouver une méthode pour générer des échantillons de fonction de fenêtre directement sur le FPGA à la volée, sans écrire les coefficients du périphérique distant dans la mémoire de bloc. Heureusement, les choses de base ont longtemps été inventées pour nous. En utilisant un algorithme tel que CORDIC (la méthode numérique par numérique ), il est possible de concevoir de nombreuses fonctions de fenêtre dont les formules sont exprimées en termes de signaux harmoniques (Blackman-Harris, Hann, Hamming, Nattal, etc.)

CORDIC

CORDIC est une méthode itérative simple et pratique pour calculer la rotation d'un système de coordonnées, qui vous permet de calculer des fonctions complexes en effectuant des opérations d'addition et de décalage primitives. En utilisant l'algorithme CORDIC, on peut calculer les valeurs des signaux harmoniques sin (x), cos (x), trouver la phase - atan (x) et atan2 (x, y), les fonctions trigonométriques hyperboliques, faire pivoter le vecteur, extraire la racine du nombre, etc.

Au début, je voulais prendre le noyau CORDIC fini et réduire la quantité de travail, mais j'ai une longue aversion pour les noyaux Xilinx. Après avoir étudié les référentiels sur le github, j'ai réalisé que tous les cœurs présentés ne conviennent pas pour un certain nombre de raisons (mal documentés et illisibles, non universels, conçus pour une tâche spécifique ou une base d'éléments, écrits en verilog , etc.). Ensuite, j'ai demandé au camarade Lazifo de faire ce travail pour moi. Bien sûr, il s'en est occupé, car la mise en œuvre de CORDIC est l'une des tâches les plus simples dans le domaine des DSP. Mais comme je suis impatient, parallèlement à son travail, j'ai écrit mon vélo avec mon propre noyau paramétré. Les principales caractéristiques sont la profondeur de bits configurable des signaux de sortie DATA_WIDTH et la phase d'entrée normalisée PHASE_WIDTH de -1 à 1, et la précision des calculs de PRECISION . Le cœur CORDIC est exécuté selon le circuit parallèle du pipeline - à chaque cycle d'horloge, le cœur est prêt à effectuer des calculs et à recevoir des échantillons d'entrée. Le noyau passe N cycles pour calculer l'échantillon de sortie, dont le nombre dépend de la capacité des échantillons de sortie (plus la capacité est grande, plus il y a d'itérations pour calculer la valeur de sortie). Tous les calculs se font en parallèle. Ainsi, CORDIC est le noyau de base pour créer des fonctions de fenêtre.

Fonctions de fenêtre

Dans le cadre de cet article, je ne réalise que les fonctions de fenêtre qui s'expriment à travers des signaux harmoniques (Hann, Hamming, Blackman-Harris de divers ordres, etc.). Que faut-il pour cela? En termes généraux, la formule de construction d'une fenêtre ressemble à une série de longueur finie.



Un certain ensemble de coefficients a _k et de membres de la série détermine le nom de la fenêtre. La fenêtre Blackman-Harris la plus populaire et la plus utilisée est d'ordre différent (de 3 à 11). Voici un tableau des coefficients pour les fenêtres Blackman-Harris:



En principe, l'ensemble de fenêtres Blackman-Harris est applicable à de nombreux problèmes d'analyse spectrale, et il n'est pas nécessaire d'essayer d'utiliser des fenêtres complexes telles que Gauss ou Kaiser. Les fenêtres nattales ou à toit plat ne sont qu'une variété de fenêtres avec des poids différents, mais les mêmes principes de base que Blackman-Harris. On sait que plus il y a de membres de la série, plus la suppression du niveau des lobes latéraux est forte (sous réserve d'un choix raisonnable de la profondeur de bits de la fonction fenêtre). En fonction de la tâche, le développeur n'a qu'à choisir le type de fenêtres utilisées.

Implémentation FPGA - approche traditionnelle

Tous les noyaux des fonctions de fenêtre sont conçus en utilisant l'approche classique pour décrire les circuits numériques dans les FPGA et sont écrits en langage VHDL. Voici une liste des composants fabriqués:

• bh_win_7term - Blackman-Harris 7 order, une fenêtre avec suppression maximale des échafaudages latéraux.
• bh_win_5term - Commande Blackman-Harris 5, comprend une fenêtre avec un dessus plat.
• bh_win_4term - Blackman-Harris 4 commandes, comprend les fenêtres Nattal et Blackman-Nattal.
• bh_win_3term - Blackman-Harris 3 commandes,
• hamming_win - Fenêtres Hamming et Hann.

Le code source du composant de fenêtre Blackman-Harris est de 3 ordres de grandeur:

entity bh_win_3term is generic ( TD : time:=0.5ns; --! Time delay PHI_WIDTH : integer:=10; --! Signal period = 2^PHI_WIDTH DAT_WIDTH : integer:=16; --! Output data width XSERIES : string:="ULTRA" --! for 6/7 series: "7SERIES"; for ULTRASCALE: "ULTRA"; ); port ( RESET : in std_logic; --! Global reset CLK : in std_logic; --! System clock AA0 : in std_logic_vector(DAT_WIDTH-1 downto 0); -- A0 AA1 : in std_logic_vector(DAT_WIDTH-1 downto 0); -- A1 AA2 : in std_logic_vector(DAT_WIDTH-1 downto 0); -- A2 ENABLE : in std_logic; --! Clock enable DT_WIN : out std_logic_vector(DAT_WIDTH-1 downto 0); --! Output DT_VLD : out std_logic --! Output data valid ); end bh_win_3term; 

Dans certains cas, j'ai utilisé la bibliothèque UNISIM pour incorporer les nœuds DSP48E1 et DSP48E2 dans le projet, ce qui me permet finalement d'augmenter la vitesse des calculs en raison du pipelining à l'intérieur de ces blocs, mais comme l'a montré la pratique, il est plus rapide et plus facile de donner libre cours et d'écrire quelque chose comme P = A * B + C et spécifiez les directives suivantes dans le code:

 attribute USE_DSP of <signal_name>: signal is "YES"; 

Cela fonctionne bien et définit de manière rigide le type d'élément sur lequel la fonction mathématique est implémentée pour le synthétiseur.

Vivado hls

De plus, j'ai implémenté tous les cœurs à l'aide des outils Vivado HLS . Je vais énumérer les principaux avantages de Vivado HLS: haute vitesse de conception ( time-to-market ) dans les langages de haut niveau C ou C ++, modélisation rapide des nœuds développés en raison de l'absence d'un concept de fréquence d'horloge, configuration flexible des solutions (en termes de ressources et de performances) en introduisant pragmas et directives dans le projet, ainsi qu'un seuil d'entrée bas pour les développeurs dans les langages de haut niveau. Le principal inconvénient est le coût sous-optimal des ressources FPGA par rapport à l'approche classique. De plus, il n'est pas possible d'atteindre les vitesses fournies par les anciennes méthodes RTL classiques (VHDL, Verilog, SV). Eh bien, le plus gros inconvénient est de danser avec un tambourin, mais cela est caractéristique de tous les CAD de Xilinx. (Remarque: dans le débogueur Vivado HLS et dans le modèle C ++ réel, des résultats souvent différents ont été obtenus, car Vivado HLS fonctionne de manière tordue en utilisant les avantages de la précision arbitraire ).

L'image suivante montre le journal du noyau CORDIC synthétisé dans Vivado HLS. Il est assez informatif et affiche de nombreuses informations utiles: la quantité de ressources utilisées, l'interface utilisateur du noyau, les boucles et leurs propriétés, le retard dans le calcul, l'intervalle de calcul de la valeur de sortie (important lors de la conception de circuits série et parallèles):



Vous pouvez également voir comment calculer les données dans divers composants (fonctions). On peut voir qu'à la phase zéro, les données de phase sont lues et aux étapes 7 et 8, le résultat du nœud CORDIC est affiché.


Le résultat de Vivado HLS: un noyau RTL synthétisé créé à partir de code C. Le journal montre que dans l'analyse de temps, le noyau réussit toutes les restrictions:



Un autre gros avantage de Vivado HLS est que pour vérifier le résultat, elle fait elle-même un banc d'essai du code RTL synthétisé basé sur le modèle qui a été utilisé pour vérifier le code C. Cela peut être un test primitif, mais je pense qu'il est très cool et assez pratique pour comparer le fonctionnement de l'algorithme en C et en HDL. Ci-dessous, une capture d'écran de Vivado montrant une simulation du modèle de fonction de noyau d'une fonction de fenêtre obtenue par Vivado HLS:



Ainsi, pour toutes les fonctions de fenêtre, des résultats similaires ont été obtenus, quelle que soit la méthode de conception - en VHDL ou en C ++. Cependant, dans le premier cas, une plus grande fréquence de fonctionnement et un plus petit nombre de ressources sont atteints, et dans le second cas, la vitesse de conception maximale est atteinte. Les deux approches ont droit à la vie.

J'ai calculé précisément combien de temps je consacrerais au développement en utilisant différentes méthodes. J'ai implémenté un projet C ++ dans Vivado HLS ~ 12 fois plus rapidement qu'en VHDL.

Comparaison des approches

Comparez le code source pour HDL et C ++ pour le noyau CORDIC. L'algorithme, comme cela a été dit précédemment, est basé sur les opérations d'addition, de soustraction et de décalage. Sur VHDL, cela ressemble à ceci: il y a trois vecteurs de données - l'un est responsable de la rotation de l'angle, et les deux autres déterminent la longueur du vecteur le long des axes X et Y, ce qui équivaut à sin et cos (voir l'image du wiki):



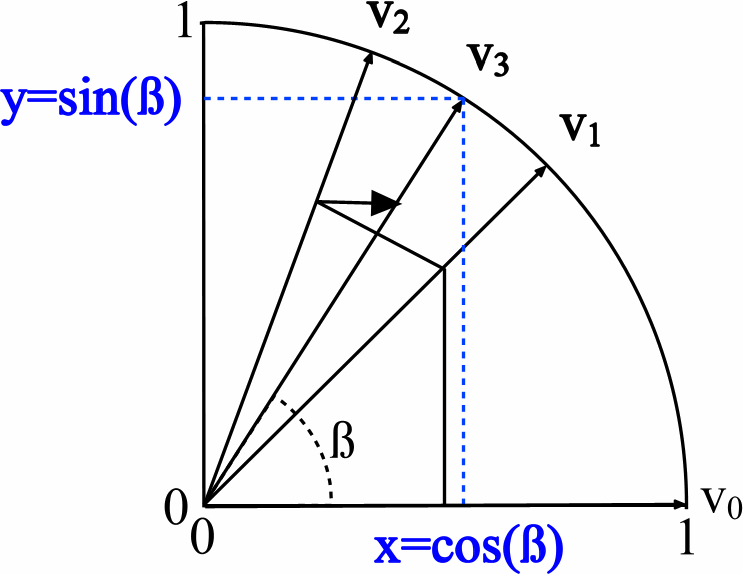
En calculant itérativement la valeur Z, les valeurs X et Y sont calculées en parallèle. Le processus de recherche cyclique des valeurs de sortie sur HDL:

 constant ROM_LUT : rom_array := ( x"400000000000", x"25C80A3B3BE6", x"13F670B6BDC7", x"0A2223A83BBB", x"05161A861CB1", x"028BAFC2B209", x"0145EC3CB850", x"00A2F8AA23A9", x"00517CA68DA2", x"0028BE5D7661", x"00145F300123", x"000A2F982950", x"000517CC19C0", x"00028BE60D83", x"000145F306D6", x"0000A2F9836D", x"0000517CC1B7", x"000028BE60DC", x"0000145F306E", x"00000A2F9837", x"00000517CC1B", x"0000028BE60E", x"00000145F307", x"000000A2F983", x"000000517CC2", x"00000028BE61", x"000000145F30", x"0000000A2F98", x"0000000517CC", x"000000028BE6", x"0000000145F3", x"00000000A2FA", x"00000000517D", x"0000000028BE", x"00000000145F", x"000000000A30", x"000000000518", x"00000000028C", x"000000000146", x"0000000000A3", x"000000000051", x"000000000029", x"000000000014", x"00000000000A", x"000000000005", x"000000000003", x"000000000001", x"000000000000" ); pr_crd: process(clk, reset) begin if (reset = '1') then ---- Reset sine / cosine / angle vector ---- sigX <= (others => (others => '0')); sigY <= (others => (others => '0')); sigZ <= (others => (others => '0')); elsif rising_edge(clk) then sigX(0) <= init_x; sigY(0) <= init_y; sigZ(0) <= init_z; ---- calculate sine & cosine ---- lpXY: for ii in 0 to DATA_WIDTH-2 loop if (sigZ(ii)(sigZ(ii)'left) = '1') then sigX(ii+1) <= sigX(ii) + sigY(ii)(DATA_WIDTH+PRECISION-1 downto ii); sigY(ii+1) <= sigY(ii) - sigX(ii)(DATA_WIDTH+PRECISION-1 downto ii); else sigX(ii+1) <= sigX(ii) - sigY(ii)(DATA_WIDTH+PRECISION-1 downto ii); sigY(ii+1) <= sigY(ii) + sigX(ii)(DATA_WIDTH+PRECISION-1 downto ii); end if; end loop; ---- calculate phase ---- lpZ: for ii in 0 to DATA_WIDTH-2 loop if (sigZ(ii)(sigZ(ii)'left) = '1') then sigZ(ii+1) <= sigZ(ii) + ROM_TABLE(ii); else sigZ(ii+1) <= sigZ(ii) - ROM_TABLE(ii); end if; end loop; end if; end process; 

En C ++, dans Vivado HLS, le code est presque identique, mais l'enregistrement est plusieurs fois plus court:

 // Unrolled loop // int k; stg: for (k = 0; k < NWIDTH; k++) { #pragma HLS UNROLL if (z[k] < 0) { x[k+1] = x[k] + (y[k] >> k); y[k+1] = y[k] - (x[k] >> k); z[k+1] = z[k] + lut_angle[k]; } else { x[k+1] = x[k] - (y[k] >> k); y[k+1] = y[k] + (x[k] >> k); z[k+1] = z[k] - lut_angle[k]; } } 

Apparemment, le même cycle avec décalage et ajouts est utilisé. Cependant, par défaut, toutes les boucles dans Vivado HLS sont «réduites» et exécutées séquentiellement, comme prévu pour le langage C ++. L'introduction du pragma HLS UNROLL ou HLS PIPELINE convertit les calculs série en parallèle. Cela conduit à une augmentation des ressources FPGA, cependant, il vous permet de calculer et de soumettre de nouvelles valeurs au cœur à chaque cycle d'horloge.

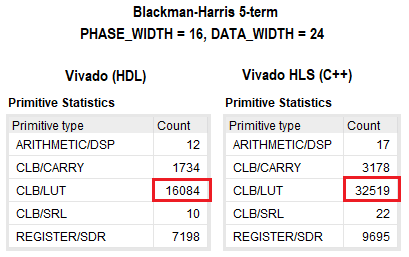
Les résultats de la synthèse du projet en VHDL et C ++ sont présentés dans la figure ci-dessous. Comme vous pouvez le voir, logiquement, la différence est deux fois en faveur de l'approche traditionnelle. Pour d'autres ressources FPGA, l'écart est insignifiant. Je n'ai pas approfondi l'optimisation du projet en C ++, mais sans ambiguïté en définissant diverses directives ou en modifiant partiellement le code, le nombre de ressources utilisées peut être réduit. Dans les deux cas, les synchronisations ont convergé pour une fréquence centrale donnée de ~ 350 MHz.

Caractéristiques d'implémentation

Étant donné que les calculs sont effectués dans un format à virgule fixe, les fonctions de fenêtre ont un certain nombre de fonctionnalités qui doivent être prises en compte lors de la conception de systèmes DSP sur FPGA. Par exemple, plus la profondeur de bits des données de fonction de fenêtre est grande, meilleure est la précision de la superposition de fenêtre. D'un autre côté, avec une profondeur de bits insuffisante de la fonction de fenêtre, des distorsions seront introduites dans la forme d'onde résultante, ce qui affectera la qualité des caractéristiques spectrales. Par exemple, une fonction de fenêtre doit avoir au moins 20 bits lorsqu'elle est multipliée par un signal d'une durée de 2 ^ 20 = 1M d'échantillons.

Conclusion

Cet article montre une façon de concevoir des fonctions de fenêtre sans utiliser de mémoire externe ou de mémoire de bloc FPGA. La méthode d'utilisation exclusive des ressources logiques des FPGA (et dans certains cas des blocs DSP) est donnée. En utilisant l'algorithme CORDIC, il est possible d'obtenir des fonctions de fenêtre de n'importe quelle profondeur de bit (dans des limites raisonnables), de n'importe quelle longueur et ordre, et donc d'avoir un ensemble de pratiquement toutes les caractéristiques spectrales de la fenêtre.

Dans le cadre de l'une des études, j'ai réussi à obtenir un noyau fonctionnant de manière stable de la fonction de fenêtre Blackman-Harris de 5 et 7 ordres de grandeur sur des échantillons de 1 M à une fréquence de ~ 375 MHz, et également à créer un générateur de coefficients rotatifs pour une FFT basée sur CORDIC à une fréquence de ~ 400 MHz. Cristal FPGA utilisé: Kintex Ultrascale + (xcku11p-ffva1156-2-e).

Lien vers le projet github ici . Le projet contient un modèle mathématique dans Matlab, des codes sources pour les fonctions de fenêtre et CORDIC en VHDL, ainsi que des modèles des fonctions de fenêtre répertoriées en C ++ pour Vivado HLS.

Articles utiles

• Fonctions de la fenêtre DSPLib
• Certaines fonctions de la fenêtre DSPlib
• Wiki de filtrage de fenêtre étendu
• Article wiki sur CORDIC
• Vivado HLS Userguide
• L'article sur l'analyse spectrale sur le Habr

Je conseille également un livre très populaire sur DSP - Ayficher E., Jervis B. Digital signal processing. Approche pratique

Merci de votre attention!