Les étudiants apprennent à connaître le problème de la ceinture de sécurité en suivant des cours de bioinformatique, en particulier, l'un des cours de bioinformatique (Pavel Pevzner) de la plus haute qualité et le plus proche dans l'esprit des programmeurs est le coursera de l'Université de Californie à San Diego. Le problème attire l'attention par la simplicité de l'énoncé, son importance pratique et par le fait qu'il est toujours considéré comme non résolu avec la capacité apparente de le résoudre avec un codage simple. Le problème se pose ainsi. Est-il possible de restaurer les coordonnées de nombreux points
en temps polynomial $ en ligne $ X $ en ligne $ si l'ensemble de toutes les distances entre elles est connu
$ en ligne $ \ Delta X $ en ligne $ ?
Cette tâche apparemment simple est toujours sur la liste des problèmes non résolus de la géométrie informatique. De plus, la situation ne concerne même pas les points dans les espaces multidimensionnels, en particulier les courbes, le problème est déjà l'option la plus simple - lorsque tous les points ont des coordonnées entières et sont localisés sur la même ligne.
Au cours des près d'un demi-siècle depuis que cette tâche a été reconnue par les mathématiciens comme un défi (Shamos, 1975), certains résultats ont été obtenus. Nous considérons deux cas possibles pour un problème unidimensionnel:
- les points sont situés sur une ligne droite (problème de péage)
- les points sont situés sur un cercle (problème de ceinture)
Ces deux cas ont reçu des noms différents pour une raison - il faut des efforts différents pour les résoudre. En effet, la première tâche a été résolue assez rapidement (en 15 ans) et un algorithme de backtracking a été construit, qui restaure la solution en moyenne en temps quadratique
$ inline $ O (n ^ 2 \ log n) $ inline $ où
$ en ligne $ n $ en ligne $ - le nombre de points (Skiena, 1990); pour la deuxième tâche, cela n'a pas été fait jusqu'à présent, et le meilleur algorithme proposé a une complexité de calcul exponentielle
$ inline $ O (n ^ n \ log n) $ inline $ (Lemke, 2003). L'image ci-dessous montre une estimation de la durée de fonctionnement de votre ordinateur pour obtenir une solution pour un ensemble avec un nombre différent de points.

Autrement dit, dans un délai psychologiquement acceptable (~ 10 sec), vous pouvez restaurer de
$ en ligne $ X $ en ligne $ jusqu'à 10 mille points dans un étui à péage et seulement ~ 10 points pour un étui de ceinture, ce qui est absolument sans valeur pour les applications pratiques.
Une petite clarification. On pense que le problème du péage est résolu en termes d'utilisation pratique, c'est-à-dire pour la grande majorité des données rencontrées. Dans ce cas, les objections des mathématiciens purs au fait qu'il existe des ensembles de données spéciaux pour lesquels le temps pour obtenir une solution de façon exponentielle est ignoré
$ inline $ O (2 ^ n \ log n) $ inline $ (Zhang, 1982). Contrairement au turnpike, le problème du périphérique avec son algorithme exponentiel ne peut être considéré comme résolu en aucune façon.
Importance de résoudre les problèmes de ceinture de sécurité en termes de bioinformatique
À la fin du 20e siècle, une nouvelle voie de synthèse des biomolécules, appelée voie de synthèse non tribosomique, a été découverte. Sa principale différence par rapport à la voie de synthèse classique est que le résultat final de la synthèse n'est pas du tout codé dans l'ADN. Au lieu de cela, seul le code des «outils» (de nombreuses synthétases différentes) qui peuvent collecter ces objets est écrit dans l'ADN. Ainsi, l'ingénierie de la biomachine est considérablement enrichie, et au lieu d'un seul type de collecteur (ribosome), qui fonctionne avec seulement 20 parties standard (acides aminés standard, également appelés protéinogéniques), de nombreux autres types de collecteurs apparaissent qui peuvent fonctionner avec plus de 500 pièces standard et non standard (acides aminés non protéinogéniques et leurs diverses modifications). Et ces assembleurs peuvent non seulement connecter des pièces en chaînes, mais également obtenir des structures très complexes - cycliques, ramifiées, ainsi que des structures avec de nombreux cycles et ramifications. Tout cela augmente considérablement l'arsenal de la cellule pour divers cas de sa vie. L'activité biologique de ces structures est élevée, la spécificité (sélectivité d'action) aussi, une variété de propriétés n'est pas limitée. La classe de ces produits cellulaires dans la littérature anglaise est appelée NRP (non-ribosomal products, or non-ribosomal peptides). Les biologistes espèrent que c'est précisément parmi ces produits du métabolisme cellulaire que l'on peut trouver de nouvelles préparations pharmacologiques qui sont très efficaces et n'ont pas d'effets secondaires en raison de la spécificité.
La seule question est, comment et où chercher des PNR? Ils sont très efficaces, donc la cellule n'a absolument pas besoin de les produire en grande quantité, et leurs concentrations sont négligeables. Ainsi, les méthodes d'extraction chimique avec leur faible précision de ~ 1% et leurs énormes coûts de réactifs et de temps sont inutiles. Ensuite. Ils ne sont pas codés dans l'ADN, ce qui signifie que toutes les bases de données accumulées lors du décodage du génome, et toutes les méthodes de bioinformatique et de génomique, sont également inutiles. La seule façon de trouver quelque chose est par des méthodes physiques, à savoir la spectroscopie de masse. De plus, le niveau de détection des substances dans les spectromètres modernes est si élevé qu'il permet de trouver des quantités insignifiantes, au total> ~ 800 molécules (plage atto-molaire, ou concentration
$ en ligne $ 10 ^ {- 18} $ en ligne $ )
"
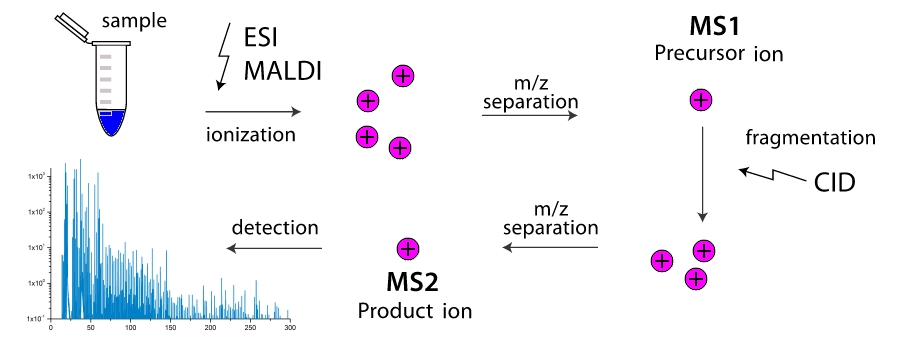
Comment fonctionne un spectromètre de masse? Dans la chambre de travail de l'appareil, les molécules sont décomposées en fragments (plus souvent par leurs collisions les unes avec les autres, moins souvent en raison d'influences externes). Ces fragments sont ionisés, puis accélérés et séparés dans un champ électromagnétique externe. La séparation se produit soit au moment où le détecteur atteint, soit par l'angle de la rotation dans le champ magnétique, car la masse du fragment est plus grande et sa charge est plus faible, plus elle est maladroite. Ainsi, le spectromètre de masse «pèse» les masses de fragments. De plus, la "pesée" peut se faire par étapes, en filtrant à plusieurs reprises des fragments de même masse (plus précisément, avec une valeur
$ en ligne $ m / z $ en ligne $ ) et les conduire à travers la fragmentation avec une séparation supplémentaire. Les spectromètres de masse à deux étages sont largement distribués et sont appelés spectromètres de masse en tandem, les spectromètres de masse à plusieurs étages sont extrêmement rares et sont simplement désignés comme
$ inline $ ms ^ n $ inline $ où
$ en ligne $ n $ en ligne $ - le nombre d'étapes. Et la tâche apparaît ici, comment, ne connaissant que les masses de toutes sortes de fragments de n'importe quelle molécule, connaître sa structure? Nous sommes donc arrivés à des problèmes de turnpike et de ceinture, pour les peptides linéaires et cycliques, respectivement.
J'expliquerai plus en détail comment la tâche de restaurer la structure d'une biomolécule est réduite aux problèmes indiqués en utilisant l'exemple d'un peptide cyclique.
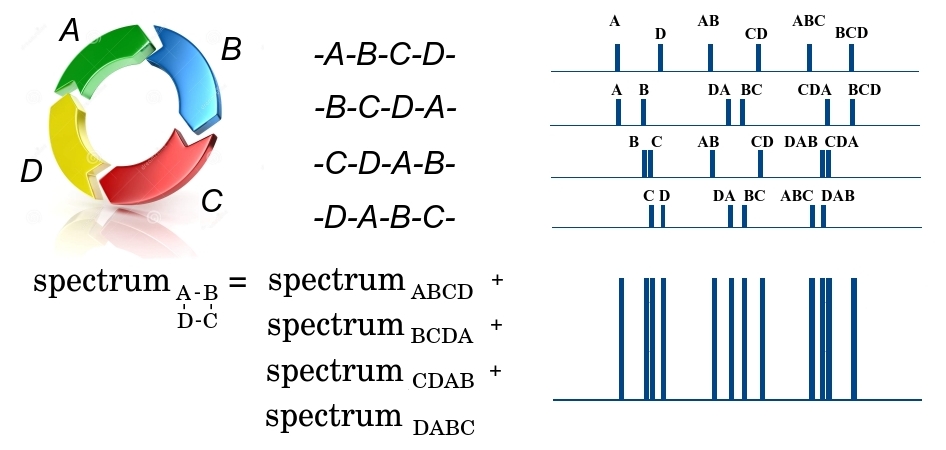
Le peptide cyclique ABCD au premier stade de la fragmentation peut être cassé en 4 endroits, soit par liaison DA, soit par AB, BC ou CD, formant 4 peptides linéaires possibles - ABCD, BCDA, CDAB ou DABC. Puisqu'un grand nombre de peptides identiques traversent le spectromètre, nous aurons des fragments des 4 types à la sortie. De plus, nous notons que tous les fragments ont la même masse et ne peuvent pas être séparés au premier stade. Dans la deuxième étape, le fragment linéaire ABCD peut être cassé en trois endroits, formant des fragments plus petits avec des masses différentes A et BCD, AB et CD, ABC et D, et formant le spectre de masse correspondant. Dans ce spectre, la masse du fragment est tracée le long de l'axe x, et le nombre de petits fragments avec une masse donnée le long de l'axe y. De même, des spectres sont formés pour les trois fragments linéaires restants de BCDA, CDAB et DABC. Puisque les 4 grands fragments sont passés au deuxième étage, tous leurs spectres sont additionnés. Au total, le résultat est une certaine masse
$ en ligne $ \ {m_1 ^ {n_1}, m_2 ^ {n_2}, .., m_q ^ {n_q} \} $ en ligne $ où
$ inline $ m_i $ inline $ - une certaine masse, et
$ inline $ n_i $ inline $ - la fréquence de sa répétition. En même temps, nous ne savons pas à quel fragment appartient cette masse et si ce fragment est unique, car différents fragments peuvent avoir une masse. Plus les liaisons dans le peptide sont éloignées les unes des autres, plus la masse du fragment peptidique est grande entre elles. Autrement dit, la tâche de restaurer l'ordre des éléments dans un peptide cyclique se réduit à un problème de ceinture, dans lequel les éléments de l'ensemble
$ en ligne $ X $ en ligne $ sont des liaisons dans le peptide et des éléments d'une multitude
$ en ligne $ \ Delta X $ en ligne $ - masses de fragments entre les liaisons.
Anticipation de l'existence d'un algorithme à temps polynomial pour résoudre les problèmes de ceinture
D'après mon expérience et de communiquer avec des gens qui ont essayé ou vraiment fait quelque chose pour résoudre ce problème, j'ai remarqué que la grande majorité des gens essaient de le résoudre soit dans le cas général, soit pour des données entières dans une plage étroite, comme celle-ci (1, 50). Les deux options sont vouées à l'échec. Pour le cas général, il a été prouvé que le nombre total de solutions aux problèmes de ceinture dans le cas unidimensionnel
$ en ligne $ S_1 (n) $ en ligne $ limité par des valeurs (Lemke, 2003)
$$ afficher $$ e ^ {2 ^ {\ frac {\ ln n} {\ ln \ ln n} + o (1)}} \ leq S_1 (n) \ leq \ frac {1} {2} n ^ {n-2} $$ afficher $$
ce qui signifie la présence d'un nombre exponentiel de solutions dans les asymptotiques
$ inline $ n \ rightarrow \ infty $ inline $ . De toute évidence, si le nombre de solutions augmente de façon exponentielle, le moment de leur réception ne peut pas augmenter plus lentement. Autrement dit, dans le cas général, il est impossible d'obtenir une solution temporelle polynomiale. Quant aux données entières dans une plage étroite, tout peut être vérifié expérimentalement, car il n'est pas trop difficile d'écrire du code qui cherche une solution par une recherche exhaustive. Pour les petits
$ en ligne $ n $ en ligne $ un tel code ne prendra pas très longtemps. Les résultats des tests d'un tel code montreront que dans de telles conditions de données, le nombre total de solutions différentes pour n'importe quel ensemble
$ en ligne $ \ Delta X $ en ligne $ déjà petit
$ en ligne $ n $ en ligne $ croît également très fortement.
Après avoir pris connaissance de ces faits, vous pouvez accepter et abandonner cette tâche. J'admets que c'est l'une des raisons pour lesquelles le problème du périphérique est toujours considéré comme non résolu. Cependant, des failles existent. Rappelons que la fonction exponentielle
$ inline $ e ^ {\ alpha x} $ inline $ se comporte très intéressant. Au début, il croît terriblement lentement, passant de 0 à 1 sur un intervalle infiniment grand de
$ inline $ \ infty $ inline $ à 0, puis sa croissance s'accélère de plus en plus. Cependant, plus la valeur est basse
$ inline $ \ alpha $ inline $ plus la valeur doit être élevée
$ en ligne $ x $ en ligne $ de sorte que le résultat de la fonction dépasse une certaine valeur définie
$ inline $ y = \ xi $ inline $ . En tant que telle valeur, il est pratique de choisir un nombre
$ inline $ \ xi = 2 $ inline $ , avant lui la seule solution, après lui il y a beaucoup de décisions. Question Et quelqu'un a-t-il vérifié la dépendance du nombre de décisions sur les données qui parviennent à l'entrée? Oui, je l'ai fait. Il existe une merveilleuse thèse de doctorat de la mathématicienne croate Tamara Dakis (Dakic, 2000), dans laquelle elle a déterminé les conditions auxquelles les données d'entrée doivent satisfaire pour que le problème soit résolu en temps polynomial. Les plus importants d'entre eux sont l'unicité de la solution et l'absence de duplication dans l'ensemble des données d'entrée.
$ en ligne $ \ Delta X $ en ligne $ . Le niveau de sa thèse de doctorat est très élevé. Il est malheureux que cette étudiante se soit limitée à un problème de péage, je suis convaincu que si elle avait tourné son intérêt vers le problème de la ceinture, cela aurait été résolu depuis longtemps.
Obtention d'un algorithme avec temps polynomial pour résoudre les problèmes de ceinture
Il a été possible de trouver les données pour lesquelles il est possible de construire l'algorithme souhaité par hasard. Il a fallu des idées supplémentaires. L'idée principale est née de l'observation (voir ci-dessus) que le spectre d'un peptide cyclique est la somme des spectres de tous les peptides linéaires qui se forment lors de ruptures d'un anneau unique. Étant donné que la séquence d'acides aminés dans un peptide peut être restaurée à partir d'un tel peptide linéaire, le nombre total de raies dans le spectre est significatif (en
$ en ligne $ n $ en ligne $ fois où
$ en ligne $ n $ en ligne $ - le nombre d'acides aminés dans le peptide) est excessif. La question est seulement de savoir quelles lignes doivent être exclues du spectre afin de ne pas perdre la capacité de restaurer la séquence. Étant donné que les deux tâches (restauration de la séquence peptidique cyclique à partir du spectre de masse et problème de ceinture) sont mathématiquement isomorphes, il est également possible d’éclaircir de nombreuses
$ en ligne $ \ Delta X $ en ligne $ .
Opérations d'éclaircie
$ en ligne $ \ Delta X $ en ligne $ ont été construits en utilisant des symétries locales de l'ensemble
$ en ligne $ \ Delta X $ en ligne $ (Fomin, 2016a).
- Symétrisation La première opération consiste à sélectionner un élément arbitraire de l'ensemble $ inline $ x _ {\ mu} \ in \ Delta X $ inline $ et retirer de $ en ligne $ \ Delta X $ en ligne $ tous les éléments sauf ceux qui ont des paires symétriques par rapport aux points $ inline $ x _ {\ mu} / 2 $ inline $ et $ inline $ (L + x _ {\ mu}) / 2 $ inline $ où $ en ligne $ L $ en ligne $ - circonférence (je rappelle que dans le cas de la ceinture de sécurité, tous les points sont situés sur le cercle).
- Convolution de solution partielle. La deuxième opération utilise la conjecture sur la solution, c'est-à-dire la connaissance des points individuels qui appartiennent à la solution, la soi-disant solution partielle. Sur plusieurs $ en ligne $ \ Delta X $ en ligne $ tous les éléments sont également supprimés, à l'exception de ceux qui remplissent la condition - si nous mesurons la distance entre le point testé et tous les points d'une solution partielle, alors toutes les valeurs obtenues sont en $ en ligne $ \ Delta X $ en ligne $ . Je précise que si au moins une des distances obtenues est absente dans $ en ligne $ \ Delta X $ en ligne $ alors le point est ignoré.
Les théorèmes ont été prouvés que les deux opérations éclaircissent l'ensemble
$ en ligne $ \ Delta X $ en ligne $ , mais il reste encore suffisamment d'éléments pour restaurer la solution
$ en ligne $ X $ en ligne $ . À l'aide de ces opérations, un algorithme a été construit et implémenté en c ++ pour résoudre le problème du périphérique (Fomin, 2016b). L'algorithme diffère peu de l'algorithme de retour arrière classique (c'est-à-dire que nous essayons de construire une solution en énumérant les options possibles et de revenir si nous obtenons une erreur pendant la construction). La seule différence est que pour rétrécir l'ensemble
$ en ligne $ \ Delta X $ en ligne $ nous tester devient beaucoup moins d'options.
Voici un exemple du nombre
$ en ligne $ \ Delta X $ en ligne $ lors de l'amincissement.

Des expériences de calcul ont été effectuées pour des peptides cycliques de longueur aléatoire
$ en ligne $ n $ en ligne $ de 10 à 1000 acides aminés (l'axe des ordonnées sur une échelle logarithmique). L'abscisse montre également sur une échelle logarithmique le nombre d'éléments dans les ensembles amincis par diverses opérations
$ en ligne $ \ Delta X $ en ligne $ en unités
$ en ligne $ n $ en ligne $ . Une telle représentation est absolument inhabituelle, je vais donc déchiffrer comment elle est lue sur un exemple. Nous regardons le diagramme de gauche. Laissez le peptide avoir une longueur
$ en ligne $ n = 100 $ en ligne $ . Pour lui, le nombre d'éléments dans l'ensemble
$ en ligne $ \ Delta X $ en ligne $ est égal
$ en ligne $ n ^ 2 = 10000 $ en ligne $ (c'est un point sur la ligne pointillée supérieure
$ en ligne $ y = n ^ 2 $ en ligne $ ) Après avoir retiré de l'ensemble
$ en ligne $ \ Delta X $ en ligne $ éléments répétitifs, nombre d'éléments dans
$ en ligne $ \ Delta X $ en ligne $ diminue à
$ en ligne $ n_D \ environ n ^ {1.9} \ environ 6300 $ en ligne $ (cercles avec croix). Après symétrisation, le nombre d'éléments tombe à
$ en ligne $ n_S \ environ n ^ {1.75} \ environ 3100 $ en ligne $ (cercles noirs), et après convolution par solution partielle à
$ en ligne $ n_C \ environ n ^ {1.35} \ environ 500 $ en ligne $ (croix). Total, le volume total de l'ensemble
$ en ligne $ \ Delta X $ en ligne $ réduit de 20 fois seulement. Pour un peptide de même longueur, mais dans le diagramme de droite, la contraction provient de
$ en ligne $ n ^ 2 = 10000 $ en ligne $ avant
$ en ligne $ N_C \ environ n \ environ 100 $ en ligne $ , c'est-à-dire 100 fois.
Notez que la génération de cas de test pour le diagramme de gauche est effectuée de sorte que le niveau de duplication
$ inline $ k_ {dup} $ inline $ dans
$ en ligne $ \ Delta X $ en ligne $ était dans la gamme de 0,1 à 0,3, et pour la droite - moins de 0,1. Le niveau de duplication est défini comme
$ inline $ k_ {dup} = 2- \ log {N_u} / \ log {n} $ inline $ où
$ inline $ N_u $ inline $ - le nombre d'éléments uniques dans l'ensemble
$ en ligne $ \ Delta X $ en ligne $ . Une telle définition donne un résultat naturel: en l'absence de doublons dans l'ensemble
$ en ligne $ \ Delta X $ en ligne $ sa puissance est égale
$ inline $ N_u = n ^ 2 $ inline $ et
$ inline $ k_ {dup} = 0 $ inline $ à la duplication maximale possible
$ inline $ N_u = n $ inline $ et
$ inline $ k_ {dup} = 1 $ inline $ . Comment rendre possible un niveau de duplication différent, je dirai un peu plus tard. Les diagrammes montrent que plus le niveau de duplication est faible, plus
$ en ligne $ \ Delta X $ en ligne $ à
$ inline $ k_ {dup} <0.1 $ inline $ nombre d'éléments amincis
$ en ligne $ \ Delta X $ en ligne $ atteint généralement sa limite
$ inline $ O (n ^ 2) \ rightarrow O (n) $ inline $ , car dans l'ensemble décimé est inférieur à
$ en ligne $ O (n) $ en ligne $ les éléments ne peuvent pas être obtenus (les opérations stockent suffisamment d'éléments pour obtenir une solution dans laquelle
$ en ligne $ n $ en ligne $ éléments). Le fait de réduire le pouvoir de
$ en ligne $ \ Delta X $ en ligne $ à la limite inférieure est très important, c'est lui qui conduit à des changements dramatiques dans la complexité informatique de l'obtention d'une solution.
Après avoir inséré des opérations d'éclaircie dans l'algorithme de retour en arrière et résolu le problème du chemin de ceinture, un analogue complet de ce dont Tamara Dakis a parlé concernant le problème du péage a été révélé. Permettez-moi de vous le rappeler. Elle a dit que pour les problèmes de péage, il est possible d'obtenir une solution en temps polynomial si la solution est unique et qu'il n'y a pas de duplication dans
$ en ligne $ \ Delta X $ en ligne $ . Il s'est avéré qu'une absence totale de duplication n'est pas nécessaire (ce n'est guère possible pour des données réelles), il suffit que son niveau soit assez faible. La figure ci-dessous montre combien de temps est nécessaire pour obtenir une solution du problème de la ceinture de sécurité en fonction de la longueur du peptide et du niveau de duplication dans
$ en ligne $ \ Delta X $ en ligne $ .

Sur la figure, les abscisses et les ordonnées sont données sur une échelle logarithmique. Cela vous permet de voir clairement si la dépendance du temps de comptage sur la longueur de la séquence
$ en ligne $ T = f (n) $ en ligne $ exponentielle (ligne droite) ou polynomiale (courbe log-forme). Comme on peut le voir sur les diagrammes, avec un faible niveau de duplication (diagramme de droite), la solution est obtenue en temps polynomial. Eh bien, pour être plus précis, la solution est obtenue en temps quadratique. Cela se produit lorsque les opérations d'amincissement réduisent la puissance de l'ensemble à une limite inférieure.
$ inline $ O (n ^ 2) \ rightarrow O (n) $ inline $ , il y a peu de points restants, retourne lorsque l'itération sur les options devient unique, et en substance l'algorithme cesse d'itérer sur les options, mais construit simplement une solution à partir de ce qui reste.
PS Eh bien, je vais révéler le dernier secret concernant la génération d'ensembles à différents niveaux de duplication. Cela est dû à la précision différente de la présentation des données. Si les données sont générées avec une faible précision (par exemple, arrondi aux nombres entiers), le niveau de duplication devient élevé, supérieur à 0,3.
Si les données sont générées avec une bonne précision, par exemple, jusqu'à 3 décimales, le niveau de duplication diminue fortement, moins de 0,1. Et d'ici suit la dernière remarque la plus importante.Pour les données réelles, dans des conditions de précision toujours plus grande des mesures, le problème de la ceinture devient résoluble en temps réel.
Littérature1. Dakic, T. (2000). Sur le problème du péage. Thèse de doctorat, Université Simon Fraser.2. Fomin. E. (2016a) Une approche simple de la reconstruction d'un ensemble de points à partir du multiset de n ^ 2 distances par paires en n ^ 2 étapes pour le problème de séquençage: I. Théorie. J Comput Biol. 2016, 23 (9): 769-75.3. Fomin. E. (2016b) Une approche simple pour la reconstruction d'un ensemble de points à partir du multiset de n ^ 2 distances par paires en n ^ 2 étapes pour le problème de séquençage: II. Algorithme. J Comput Biol. 2016, 23 (12): 934-942.4. Lemke, P., Skiena, S. et Smith, W. (2003). Reconstruire des ensembles à partir de distances entre points. Algorithmes de géométrie discrète et de calcul et combinatoire, 25: 597–631.5. Skiena, S., Smith, W. et Lemke, P. (1990). Reconstruire des ensembles à partir de distances entre points. Dans Actes du sixième Symposium ACM sur la géométrie computationnelle, pages 332–339. Berkeley, CA6. Zhang, Z. 1982. Un exemple exponentiel pour un algorithme de cartographie de résumé partiel. J. Comp. Biol. 1, 235-240.