Implémentation de l'algorithme k-means (k-means) en utilisant l'exemple du travail avec les pixels

Bonjour à tous! Récemment, il a été nécessaire d'écrire du code pour implémenter la segmentation d'image en utilisant la méthode k-means (anglais k-means). Eh bien, la première chose que Google fait est d'aider. J'ai trouvé beaucoup d'informations, comme d'un point de vue mathématique (toutes sortes de gribouillis mathématiques complexes là-bas, vous comprendrez ce que l'enfer y est écrit), ainsi que certaines implémentations logicielles qui sont sur Internet en anglais. Ces codes sont certainement beaux - sans aucun doute, mais l'essence de l'idée est difficile à saisir. D'une manière ou d'une autre, tout est compliqué, confus, et pourtant, à la main, à la main, vous n'écrirez pas le code, vous ne comprendrez rien. Dans cet article, je veux montrer une mise en œuvre simple, non productive, mais, je l'espère, compréhensible de ce merveilleux algorithme. D'accord, allons-y!

Alors, qu'est-ce que le clustering en termes de nos perceptions? Permettez-moi de vous donner un exemple, disons qu'il y a une belle photo avec des fleurs du chalet de votre grand-mère.



La question est: pour déterminer combien de zones sur cette photo sont remplies d'environ la même couleur. Eh bien, ce n’est pas du tout difficile: des pétales blancs - un, des centres jaunes - deux (je ne suis pas biologiste, je ne sais pas comment on les appelle), trois verts. Ces sections sont appelées clusters. Un cluster est une combinaison de données ayant des caractéristiques communes (couleur, position, etc.). Le processus de détermination et de placement de chaque composant des données dans de tels clusters - sections est appelé clustering.

Il existe de nombreux algorithmes de clustering, mais le plus simple d'entre eux est k-medium, qui sera discuté plus tard. K-means est un algorithme simple et efficace, facile à mettre en œuvre à l'aide d'une méthode logicielle. Les données que nous distribuerons en grappes sont des pixels. Comme vous le savez, un pixel de couleur a trois composants - rouge, vert et bleu. L'imposition de ces composants crée ainsi une palette de couleurs existantes.



Dans la mémoire de l'ordinateur, chaque composante de couleur est caractérisée par un nombre compris entre 0 et 255. Autrement dit, en combinant différentes valeurs de rouge, vert et bleu, nous obtenons une palette de couleurs à l'écran.

En utilisant des pixels comme exemple, nous implémentons notre algorithme. K-means est un algorithme itératif, c'est-à-dire qu'il donnera le résultat correct, après un certain nombre de répétitions de certains calculs mathématiques.

Algorithme

1. Vous devez savoir à l'avance de combien de clusters vous avez besoin pour distribuer les données. C'est un inconvénient important de cette méthode, mais ce problème est résolu par des implémentations améliorées de l'algorithme, mais cela, comme on dit, est une histoire complètement différente.
2. Nous devons choisir les centres initiaux de nos grappes. Comment? Oui au hasard. Pourquoi? Pour que vous puissiez accrocher chaque pixel au centre du cluster. Le centre est comme le roi, autour duquel ses sujets sont rassemblés - les pixels. C'est la «distance» du centre au pixel qui détermine à qui chaque pixel obéira.
3. Nous calculons la distance de chaque centre à chaque pixel. Cette distance est considérée comme la distance euclidienne entre les points dans l'espace, et dans notre cas, comme la distance entre les trois composantes de couleur:

   $$$$ affiche $$ \ sqrt {(R_ {2} -R_ {1}) ^ 2 + (G_ {2} -G_ {1}) ^ 2 + (B_ {2} -B_ {1}) ^ 2} . $$ afficher $$

   Nous calculons la distance du premier pixel à chaque centre et déterminons la plus petite distance entre ce pixel et les centres. Pour le centre, dont la distance est la plus petite, nous recalculons les coordonnées comme moyenne arithmétique entre chaque composante du pixel - le roi et le pixel - du sujet. Notre centre se déplace dans l'espace selon les calculs.
4. Après avoir recompté tous les centres, nous distribuons les pixels en grappes, en comparant la distance de chaque pixel aux centres. Un pixel est placé dans un cluster, au centre duquel il est plus proche que les autres centres.
5. Tout recommence, tant que les pixels restent dans les mêmes grappes. Souvent, cela peut ne pas se produire, car avec une grande quantité de données, les centres se déplacent dans un petit rayon et les pixels le long des bords des clusters sautent dans l'un ou l'autre cluster. Pour ce faire, déterminez le nombre maximal d'itérations.

Implémentation

Je vais implémenter ce projet en C ++. Le premier fichier est «k_means.h», dans lequel j'ai défini les principaux types de données, les constantes et la classe principale pour travailler - «K_means».
Pour caractériser chaque pixel, créez une structure qui se compose de trois composants de pixel, pour lesquels j'ai choisi le type double pour des calculs plus précis, et défini également quelques constantes pour que le programme fonctionne:

const int KK = 10; //  const int max_iterations = 100; //   typedef struct { double r; double g; double b; } rgb; 

K_means se classe:

 class K_means { private: std::vector<rgb> pixcel; int q_klaster; int k_pixcel; std::vector<rgb> centr; void identify_centers(); inline double compute(rgb k1, rgb k2) { return sqrt(pow((k1.r - k2.r),2) + pow((k1.g - k2.g), 2) + pow((k1.b - k2.b), 2)); } inline double compute_s(double a, double b) { return (a + b) / 2; }; public: K_means() : q_klaster(0), k_pixcel(0) {}; K_means(int n, rgb *mas, int n_klaster); K_means(int n_klaster, std::istream & os); void clustering(std::ostream & os); void print()const; ~K_means(); friend std::ostream & operator<<(std::ostream & os, const K_means & k); }; 

Passons en revue les composants de la classe:

vectorpixcel - un vecteur pour les pixels;
q_klaster - nombre de clusters;
k_pixcel - nombre de pixels;
vectorcentr - un vecteur pour regrouper les centres, le nombre d'éléments qu'il contient est déterminé par q_klaster;
identifier_centers () - une méthode pour sélectionner aléatoirement les centres initiaux parmi les pixels d'entrée;
compute () et compute_s () sont des méthodes intégrées pour calculer la distance entre les pixels et les centres de recalcul, respectivement;
trois constructeurs: le premier par défaut, le second pour initialiser les pixels du tableau, le troisième pour initialiser les pixels d'un fichier texte (dans mon implémentation, le fichier est d'abord accidentellement rempli de données, puis les pixels sont lus à partir de ce fichier pour que le programme fonctionne, pourquoi pas directement dans le vecteur - juste nécessaire dans mon cas);
clustering (std :: ostream & os) - méthode de clustering;
méthode et surcharge de l'instruction de sortie pour publier les résultats.

Implémentation de la méthode:

 void K_means::identify_centers() { srand((unsigned)time(NULL)); rgb temp; rgb *mas = new rgb[q_klaster]; for (int i = 0; i < q_klaster; i++) { temp = pixcel[0 + rand() % k_pixcel]; for (int j = i; j < q_klaster; j++) { if (temp.r != mas[j].r && temp.g != mas[j].g && temp.b != mas[j].b) { mas[j] = temp; } else { i--; break; } } } for (int i = 0; i < q_klaster; i++) { centr.push_back(mas[i]); } delete []mas; } 

Il s'agit d'une méthode pour sélectionner les centres de regroupement initiaux et les ajouter au vecteur central. Une vérification est effectuée pour répéter les centres et les remplacer dans ces cas.

 K_means::K_means(int n, rgb * mas, int n_klaster) { for (int i = 0; i < n; i++) { pixcel.push_back(*(mas + i)); } q_klaster = n_klaster; k_pixcel = n; identify_centers(); } 

Une implémentation de constructeur pour initialiser des pixels à partir d'un tableau.

 K_means::K_means(int n_klaster, std::istream & os) : q_klaster(n_klaster) { rgb temp; while (os >> temp.r && os >> temp.g && os >> temp.b) { pixcel.push_back(temp); } k_pixcel = pixcel.size(); identify_centers(); } 

Nous passons un objet d'entrée à ce constructeur pour pouvoir entrer des données à la fois du fichier et de la console.

 void K_means::clustering(std::ostream & os) { os << "\n\n :" << std::endl; /*             :        ,    -  ,    ,   ,        .*/ std::vector<int> check_1(k_pixcel, -1); std::vector<int> check_2(k_pixcel, -2); int iter = 0; /* .*/ while(true) { os << "\n\n----------------  №" << iter << " ----------------\n\n"; { for (int j = 0; j < k_pixcel; j++) { double *mas = new double[q_klaster]; /*  :          .      ,   .*/ for (int i = 0; i < q_klaster; i++) { *(mas + i) = compute(pixcel[j], centr[i]); os << "   " << j << "   #" << i << ": " << *(mas + i) << std::endl; } /*     m_k      .*/ double min_dist = *mas; int m_k = 0; for (int i = 0; i < q_klaster; i++) { if (min_dist > *(mas + i)) { min_dist = *(mas + i); m_k = i; } } os << "    #" << m_k << std::endl; os << "  #" << m_k << ": "; centr[m_k].r = compute_s(pixcel[j].r, centr[m_k].r); centr[m_k].g = compute_s(pixcel[j].g, centr[m_k].g); centr[m_k].b = compute_s(pixcel[j].b, centr[m_k].b); os << centr[m_k].r << " " << centr[m_k].g << " " << centr[m_k].b << std::endl; delete[] mas; } /*   .*/ int *mass = new int[k_pixcel]; os << "\n  : "<< std::endl; for (int k = 0; k < k_pixcel; k++) { double *mas = new double[q_klaster]; /*    .*/ for (int i = 0; i < q_klaster; i++) { *(mas + i) = compute(pixcel[k], centr[i]); os << "   №" << k << "   #" << i << ": " << *(mas + i) << std::endl; } /*  .*/ double min_dist = *mas; int m_k = 0; for (int i = 0; i < q_klaster; i++) { if (min_dist > *(mas + i)) { min_dist = *(mas + i); m_k = i; } } mass[k] = m_k; os << " №" << k << "     #" << m_k << std::endl; } /*            .*/ os << "\n    : \n"; for (int i = 0; i < k_pixcel; i++) { os << mass[i] << " "; check_1[i] = *(mass + i); } os << std::endl << std::endl; os << " : " << std::endl; int itr = KK + 1; for (int i = 0; i < q_klaster; i++) { os << " #" << i << std::endl; for (int j = 0; j < k_pixcel; j++) { if (mass[j] == i) { os << pixcel[j].r << " " << pixcel[j].g << " " << pixcel[j].b << std::endl; mass[j] = ++itr; } } } delete[] mass; /*    .*/ os << " : \n" ; for (int i = 0; i < q_klaster; i++) { os << centr[i].r << " " << centr[i].g << " " << centr[i].b << " - #" << i << std::endl; } } /*         –  .*/ iter++; if (check_1 == check_2 || iter >= max_iterations) { break; } check_2 = check_1; } os << "\n\n ." << std::endl; } 

La principale méthode de clustering.

 std::ostream & operator<<(std::ostream & os, const K_means & k) { os << " : " << std::endl; for (int i = 0; i < k.k_pixcel; i++) { os << k.pixcel[i].r << " " << k.pixcel[i].g << " " << k.pixcel[i].b << " - №" << i << std::endl; } os << std::endl << "   : " << std::endl; for (int i = 0; i < k.q_klaster; i++) { os << k.centr[i].r << " " << k.centr[i].g << " " << k.centr[i].b << " - #" << i << std::endl; } os << "\n : " << k.q_klaster << std::endl; os << " : " << k.k_pixcel << std::endl; return os; } 

La sortie des données initiales.

Exemple de sortie

Cet exemple est prévu à l'avance, les pixels sont sélectionnés spécifiquement pour la démonstration. Deux itérations suffisent pour que le programme regroupe les données en trois clusters. En regardant les centres des deux dernières itérations, vous pouvez voir qu'ils sont pratiquement restés en place.

Plus intéressants sont les cas de pixels générés aléatoirement. Ayant généré 50 points qui doivent être divisés en 10 grappes, j'ai obtenu 5 itérations. Ayant généré 50 points qui doivent être divisés en 3 clusters, j'ai obtenu les 100 itérations maximales autorisées. Vous pouvez remarquer que plus il y a de clusters, plus il est facile pour le programme de trouver les pixels les plus similaires et de les combiner en petits groupes, et vice versa - s'il y a peu de clusters et qu'il y a beaucoup de points, l'algorithme se termine souvent uniquement lorsque le nombre maximum d'itérations est dépassé, car certains pixels sautent constamment d'un cluster à l'autre. Cependant, la majeure partie est encore complètement déterminée dans leurs grappes.

Eh bien, vérifions maintenant le résultat du clustering. En prenant le résultat de certains clusters de l'exemple de 50 points pour 10 clusters, j'ai conduit le résultat de ces données dans Illustrator et c'est ce qui s'est passé:



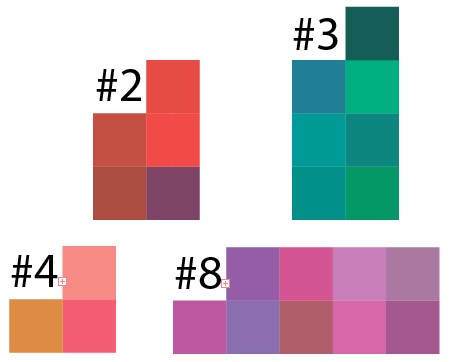
On peut voir que dans chaque groupe, toutes les nuances de couleur prévalent, et ici vous devez comprendre que les pixels ont été sélectionnés au hasard, l'analogue d'une telle image dans la vie réelle est une sorte d'image sur laquelle toutes les couleurs ont été accidentellement pulvérisées et il est difficile de sélectionner des zones de couleurs similaires.

Disons que nous avons une telle photo. Nous pouvons définir une île comme un seul cluster, mais avec une augmentation, nous voyons qu'elle se compose de différentes nuances de vert.



Et c'est le cluster 8, mais dans une version plus petite, le résultat est similaire:



La version complète du programme peut être consultée sur mon GitHub .