Des maths divertissantes. Le système de numérotation le plus économique

Nous savons tous, grâce au cours de l'école, quel est le système numérique (SS). Mais tout le monde ne pense pas à la quantité de SS. C'est-à-dire de quel ensemble de nombres nous avons besoin pour représenter le nombre dans ce SS. Lorsque nous avons un ensemble limité d'éléments uniques (cailloux multicolores de différentes tailles) avec lesquels nous pouvons représenter un nombre, quel est le nombre maximum que nous pouvons représenter en utilisant ces éléments? (tous les cailloux rouges sont nuls, les verts sont un, les bleus sont deux, etc., les petits sont nuls, les moyens sont les premiers, les grands sont les seconds, etc.). Où est la ligne sur laquelle la base du SS joue un rôle plus important que la capacité numérique du numéro?

Prenons par exemple n - le nombre d'éléments égal à 60. Après avoir divisé les éléments en 2 groupes (système de nombres binaires), nous obtenons 30 chiffres. 30 unités est le plus grand nombre de 30 bits avec une base de 2. Si vous en ajoutez 1, vous obtenez une unité avec 30 zéros, c'est-à-dire 2 au 30, puisque chaque zéro est une puissance de deux, et les chiffres commencent à 0, et n'oubliez pas de soustraire l'unité qui a été ajoutée.

Pour les autres SS, de même $$$y = x ^ {60 / x} -1$où y est le nombre maximum, x est la base du degré.

Points de construction:

$$$2 ^ {30} -1 = 1 \, 073 \, 741 \, 823$.
$$$3 ^ {20} -1 = 3 \, 486 \, 784 \, 400$.
$$$4 ^ {15} -1 = 1 \, 073 \, 741 \, 823$
$$
$$
$$
$$

Graphique de fonction:



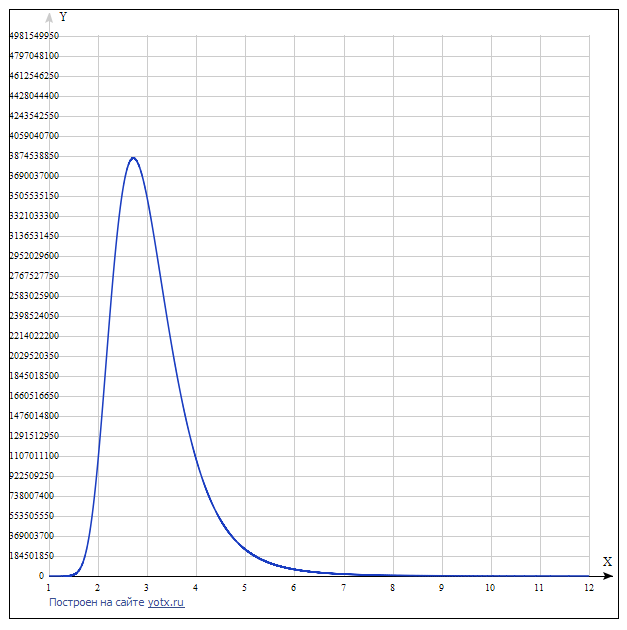
Le graphique montre qu'avec une augmentation de la base du SS, à partir de trois, son coût augmente et la fonction a un extremum supérieur. Apportant une forme générale, vous pouvez obtenir $$$y = (\ sqrt [x] x) ^ {n} -1$et la fonction maximale $$$\ sqrt [x] x$atteint lorsque $$$x = e$.



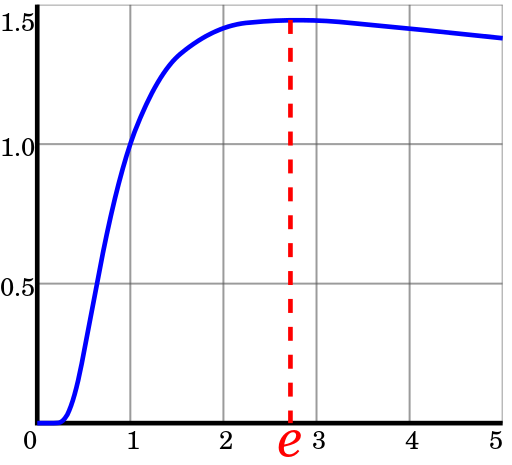
Graphique de fonction $$$y = \ sqrt [x] x$

C'est-à-dire le SS le plus économique est un système aussi proche que possible de $$$e$ou 3.

PS: De plus, le SS avec base 3 est impair, ce qui signifie qu'il n'a pas de problème d'arrondi (amenez 0,5 à 0 ou à 1), et si les nombres sont écrits symétriquement (-1,0,1 au lieu de 0,1,2) alors simplicité représentent des nombres négatifs (10-1 est 8, -101 est -8, où moins n'est pas un signe, mais une partie d'un chiffre qui peut être remplacé par Z), mais c'est une arithmétique complètement différente)))