Comment rendre encore plus indescriptibles des états encore plus invalides

Il n'y a pas si longtemps, un article a été traduit chez Habr sur la façon d'utiliser les types de données algébriques pour garantir que les états incorrects sont inexprimables. Aujourd'hui, nous examinons un moyen un peu plus généralisé, évolutif et sûr d'exprimer l'inexprimable, et le Haskell nous aidera à cet égard.

En bref, cet article traite d'une entité avec une adresse postale et une adresse e-mail, ainsi qu'à la condition supplémentaire qu'il doit y avoir au moins une de ces adresses. Comment est-il proposé d'exprimer cette condition au niveau du type? Il est proposé d'écrire les adresses comme suit:

type ContactInfo = | EmailOnly of EmailContactInfo | PostOnly of PostalContactInfo | EmailAndPost of EmailContactInfo * PostalContactInfo 

Quels sont les problèmes de cette approche?

Le plus évident (et noté plusieurs fois dans les commentaires sur cet article) est que cette approche n'est pas du tout évolutive. Imaginez que nous n’ayons pas deux types d’adresses, mais trois ou cinq, et que la condition d’exactitude ressemble à «il doit y avoir soit une adresse postale, soit à la fois une adresse électronique et une adresse de bureau, et il ne devrait pas y avoir plusieurs adresses du même type». Ceux qui le souhaitent peuvent écrire le type approprié comme exercice d'auto-test. La tâche avec un astérisque est de réécrire ce type dans le cas où la condition d'absence de doublons a disparu du TOR.

Partagez

Comment résoudre ce problème? Essayons de fantasmer. Tout d'abord, nous décomposons et séparons la classe d'adresses (par exemple, le numéro de courrier / e-mail / bureau au bureau) et le contenu correspondant à cette classe:

 data AddrType = Post | Email | Office 

Nous ne penserons pas encore au contenu, car il n'y a rien dans le cahier des charges pour la validité de la liste d'adresses.

Si nous vérifions la condition correspondante dans le runtime d'un constructeur d'un langage OOP ordinaire, alors nous écririons simplement une fonction comme

 valid :: [AddrType] -> Bool valid xs = let hasNoDups = nub xs == xs --      hasPost = Post `elem` xs hasEmail = Email `elem` xs hasOffice = Office `elem` xs in hasNoDups && (hasPost || (hasEmail && hasOffice)) 

et lancerait une exécution si elle renvoie False .

Pouvons-nous plutôt vérifier une condition similaire à l'aide d'un minuteur lors de la compilation? Il s'avère que oui, nous pouvons, si le système de type de la langue est suffisamment expressif, et le reste de l'article nous choisirons cette approche.

Ici, les types dépendants nous aideront beaucoup, et comme la façon la plus adéquate d'écrire un code validé dans Haskell est de l'écrire d'abord dans Agde ou Idris, nous allons changer de chaussures et écrire dans Idris. La syntaxe idris est assez proche de Haskell: par exemple, avec la fonction susmentionnée, il suffit de modifier légèrement la signature:

 valid : List AddrType -> Bool 

Souvenez-vous maintenant qu'en plus des classes d'adresses, nous avons également besoin de leur contenu et encodons la dépendance des champs sur la classe d'adresses en tant que GADT:

 data AddrFields : AddrType -> Type where PostFields : (city : String) -> (street : String) -> AddrFields Post EmailFields : (email : String) -> AddrFields Email OfficeFields : (floor : Int) -> (desk : Nat) -> AddrFields Office 

Autrement dit, si on nous donne une valeur de fields type AddrFields t , alors nous savons que t est une AddrType AddrType et que les fields contiennent un ensemble de champs correspondant à cette classe particulière.

 addrFields : AddrType -> Type addrFields Post = PostFields addrFields Email = EmailFields addrFields Office = OfficeFields 

Quelle est l'adresse complète de ce modèle? Il s'agit d'une paire de la classe d'adresses et des champs correspondants:

 Addr : Type Addr = (t : AddrType ** AddrFields t) 

Les fans de la théorie des types diront qu'il s'agit d'un type dépendant de l'existence: si l'on nous donne une valeur de type Addr , cela signifie qu'il existe une valeur t type AddrType et un ensemble correspondant de champs AddrFields t . Naturellement, les adresses d'une classe différente sont du même type:

 someEmailAddr : Addr someEmailAddr = (Email ** EmailFields "that@feel.bro") someOfficeAddr : Addr someOfficeAddr = (Office ** OfficeFields (-2) 762) 

De plus, si EmailFields est donné, alors la seule classe d'adresse qui convient est Email , donc vous pouvez l'omettre, le temporisateur l'imprimera vous-même:

 someEmailAddr : Addr someEmailAddr = (_ ** EmailFields "that@feel.bro") someOfficeAddr : Addr someOfficeAddr = (_ ** OfficeFields (-2) 762) 

Nous écrivons une fonction auxiliaire qui donne la liste correspondante des classes d'adresses de la liste d'adresses, et la généralisons immédiatement pour travailler sur un foncteur arbitraire:

 types : Functor f => f Addr -> f AddrType types = map fst 

Ici, le type existentiel Addr se comporte comme un couple familier: en particulier, vous pouvez demander son premier composant AddrType (tâche avec un astérisque: pourquoi ne puis-je pas demander le deuxième composant?).

Augmenter

Nous passons maintenant à un élément clé de notre histoire. Nous avons donc une liste d'adresses valid : List AddrType -> Bool et un prédicat valid : List AddrType -> Bool , dont nous voulons garantir l'exécution pour cette liste au niveau des types. Comment les combinons-nous? Bien sûr, un autre type!

 data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> (prf : valid (types lst) = True) -> ValidatedAddrList lst 

Nous allons maintenant analyser ce que nous avons écrit ici.

data ValidatedAddrList : List Addr -> Type where signifie que le type ValidatedAddrList paramétré, en fait, par la liste d'adresses.

Voyons la signature du seul constructeur MkValidatedAddrList de ce type: (lst : List Addr) -> (prf : valid (types lst) = True) -> ValidatedAddrList lst . Autrement dit, il prend une liste d'adresses prf et un autre argument prf de type valid (types lst) = True . Que signifie ce type? Cela signifie donc que la valeur à gauche de = est égale à la valeur à droite de = , c'est-à-dire valid (types lst) , en fait, est True.

Comment ça marche? Signature = ressemble à (x : A) -> (y : B) -> Type . Autrement dit, = prend deux valeurs arbitraires x et y (peut-être même de types différents A et B , ce qui signifie que l'inégalité dans l'idris est hétérogène et qu'elle est quelque peu ambiguë du point de vue de la théorie des types, mais c'est un sujet pour une autre discussion). Qu'est-ce qui démontre alors l'égalité? Et du fait que le seul constructeur = - Refl avec une signature de presque (x : A) -> x = x . Autrement dit, si nous avons une valeur de type x = y , alors nous savons qu'elle a été construite à l'aide de Refl (car il n'y a pas d'autres constructeurs), ce qui signifie que x est en fait égal à y .

Notez que c'est pourquoi dans le Haskell, nous prétendrons toujours au mieux que nous prouvons quelque chose, car le Haskell a undefined qui habite n'importe quel type, donc l'argument ci-dessus ne fonctionne pas là: pour tout x , y terme de type x = y pourrait être créé via undefined (ou par une récursion infinie, disons qu'en gros c'est la même chose en termes de théorie des types).

Nous notons également que l'égalité ici n'est pas signifiée dans le sens de Haskell Eq ou d'un operator== en C ++, mais beaucoup plus rigoureuse: structurelle, ce qui, simplifiant, signifie que les deux valeurs ont la même forme . Autrement dit, le tromper ne fonctionne tout simplement pas. Mais les questions d'égalité sont traditionnellement attirées dans un article distinct.

Afin de consolider notre compréhension de l'égalité, nous écrivons des tests unitaires pour la fonction valid :

 testPostValid : valid [Post] = True testPostValid = Refl testEmptyInvalid : valid [] = False testEmptyInvalid = Refl testDupsInvalid : valid [Post, Post] = False testDupsInvalid = Refl testPostEmailValid : valid [Post, Email] = True testPostEmailValid = Refl 

Ces tests sont bons car vous n'avez même pas besoin de les exécuter, il suffit que le taypcher les ait vérifiés. En effet, remplaçons True par False , par exemple, dans le tout premier et voyons ce qui se passe:

 testPostValid : valid [Post] = False testPostValid = Refl 

Typsekher jure

comme prévu. Super

Simplifier

Maintenant, refactorisons ValidatedAddrList peu notre ValidatedAddrList .

Tout d'abord, le modèle de comparaison d'une certaine valeur avec True assez courant, il y a donc un type spécial So dans l'idris pour cela: vous pouvez prendre So x comme synonyme de x = True . Corrigeons la définition de ValidatedAddrList :

 data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> (prf : So (valid $ types lst)) -> ValidatedAddrList lst 

De plus, So a une fonction auxiliaire pratique à choose , ce qui élève essentiellement la vérification au niveau des types:

 > :doc choose Data.So.choose : (b : Bool) -> Either (So b) (So (not b)) Perform a case analysis on a Boolean, providing clients with a So proof 

Cela nous sera utile lorsque nous écrirons des fonctions qui modifient ce type.

Deuxièmement, parfois (en particulier dans le développement interactif) idris peut trouver par lui-même la valeur prf appropriée. Pour que dans de tels cas, il n'était pas nécessaire de le construire à la main, il existe un sucre syntaxique correspondant:

 data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> {auto prf : So (valid $ types lst)} -> ValidatedAddrList lst 

Les accolades signifient qu'il s'agit d'un argument implicite qu'idris essaiera de sortir du contexte, et auto signifie qu'il essaiera également de le construire lui-même.

Alors, que nous apporte ce nouveau ValidatedAddrList ? Et cela donne une telle chaîne de raisonnement: soit val une valeur de type ValidatedAddrList lst . Cela signifie que lst est une liste d'adresses, et en outre, val été créé à l'aide du constructeur MkValidatedAddrList , auquel nous avons transmis ce très prf et une autre valeur prf de type So (valid $ types lst) , qui est presque valid (types lst) = True . Et pour que nous puissions construire prf , nous devons, en fait, prouver que cette égalité est valable.

Et le plus beau, c'est que tout est vérifié par un tympher. Oui, la vérification de validité devra être effectuée en runtime (car les adresses peuvent être lues à partir d'un fichier ou du réseau), mais le temporisateur s'assurera que cette vérification est effectuée: sans elle, il est impossible de créer une ValidatedAddrList . Au moins dans idris. À Haskell, hélas.

Insérer

Pour vérifier l'inévitabilité de la vérification, essayez d'écrire une fonction pour ajouter une adresse à la liste. Première tentative:

 insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) insert addr (MkValidatedAddrList lst) = MkValidatedAddrList (addr :: lst) 

Non, le typo-vérificateur donne sur les doigts (bien que peu lisible, le coût de la valid trop compliqué):

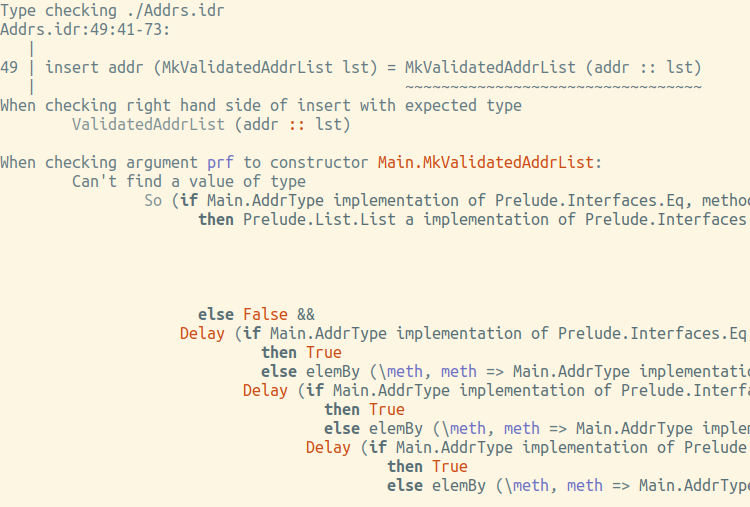
Comment obtenir une copie de ce document? Pas autrement que le choose susmentionné. Deuxième tentative:

 insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => MkValidatedAddrList (addr :: lst) Right r => ?rhs 

Il a presque typechetsya. "Presque" car on ne sait pas trop quoi substituer à rhs . C'est plutôt clair: dans ce cas, la fonction doit en quelque sorte signaler une erreur. Vous devez donc modifier la signature et encapsuler la valeur de retour, par exemple, dans Maybe - Maybe :

 insert : (addr : Addr) -> ValidatedAddrList lst -> Maybe (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => Just $ MkValidatedAddrList (addr :: lst) Right r => Nothing 

Ceci est carrelé et fonctionne comme il se doit.

Mais maintenant se pose le problème peu évident suivant, qui était, en fait, dans l'article original. Le type de cette fonction n'arrête pas d'écrire une telle implémentation:

 insert : (addr : Addr) -> ValidatedAddrList lst -> Maybe (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = Nothing 

Autrement dit, nous disons toujours que nous ne pouvions pas construire une nouvelle liste d'adresses. Typhechaetsya? Oui Est-ce correct? Enfin, à peine. Cela peut-il être évité?

Il s'avère que c'est possible, et nous avons tous les outils nécessaires pour cela. En cas de succès, insert renvoie un ValidatedAddrList , qui contient des preuves de ce succès. Ajoutez donc une symétrie élégante et demandez à la fonction de renvoyer également une preuve d'échec!

 insert : (addr : Addr) -> ValidatedAddrList lst -> Either (So (not $ valid $ types (addr :: lst))) (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => Right $ MkValidatedAddrList (addr :: lst) Right r => Left r 

Maintenant, nous ne pouvons pas simplement prendre et toujours retourner Nothing .

Vous pouvez faire de même pour les fonctions de suppression d'adresses et autres.

Voyons à quoi tout cela ressemble à la fin.

Essayons de créer une liste d'adresses vide:

C'est impossible, une liste vide n'est pas valide.

Que diriez-vous d'une liste d'une simple adresse postale?

D'accord, essayons d'insérer l'adresse postale dans la liste qui a déjà l'adresse postale:

Essayons d'insérer l'e-mail:

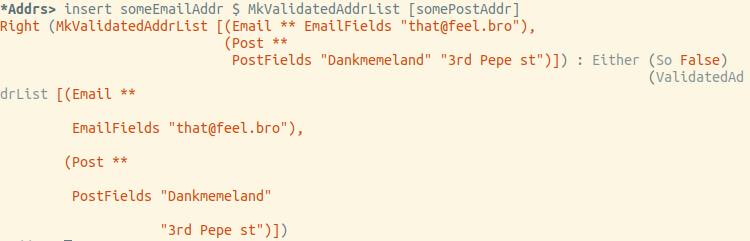
Au final, tout fonctionne exactement comme prévu.

Ouf. Je pensais que ce serait trois lignes, mais cela s'est avéré un peu plus long. Donc, pour explorer jusqu'où nous pouvons aller dans le Haskell, nous serons dans le prochain article. En attendant, un peu

Méditer

Quel est, au final, le bénéfice d'une telle décision par rapport à celle donnée dans l'article, que nous avons évoqué au tout début?

1. Il est, encore une fois, beaucoup plus évolutif. Les fonctions de validation complexes sont plus faciles à écrire.
2. C'est plus isolé. Le code client n'a pas besoin de savoir ce qu'il y a à l'intérieur de la fonction de validation, alors que le formulaire ContactInfo de l'article d'origine nécessite qu'il soit lié.
3. La logique de validation est écrite sous la forme de fonctions ordinaires et familières, de sorte qu'elle peut être vérifiée immédiatement avec une lecture réfléchie et testée avec des tests de temps de compilation, plutôt que de dériver le sens de la validation à partir d'un formulaire de type de données qui représente un résultat déjà vérifié.
4. Il devient possible de spécifier plus précisément le comportement des fonctions qui fonctionnent avec le type de données qui nous intéresse, notamment en cas d'échec au test. Par exemple, l' insert écrite en conséquence est tout simplement impossible à écrire de manière incorrecte . De même, on pourrait écrire insertOrReplace , insertOrIgnore et similaires, dont le comportement est entièrement spécifié dans le type.

Quel est le profit par rapport à une solution OOP comme ça?

 class ValidatedAddrListClass { public: ValidatedAddrListClass(std::vector<Addr> addrs) { if (!valid(addrs)) throw ValidationError {}; } }; 

1. Le code est plus modularisé et sécurisé. Dans le cas ci-dessus, une vérification est une action qui est vérifiée une fois, et à propos de laquelle ils ont ensuite oublié. Tout est basé sur l'honnêteté et la compréhension que si vous avez une ValidatedAddrListClass , alors sa mise en œuvre a fait une fois une vérification. Le fait de cette vérification de la classe ne peut pas être choisi comme une certaine valeur. Dans le cas d'une valeur d'un certain type, cette valeur peut être transférée entre différentes parties du programme, utilisée pour créer des valeurs plus complexes (par exemple, encore une fois, refuser cette vérification), enquêter (voir le paragraphe suivant) et généralement faire la même chose que nous le faisions auparavant avec des valeurs.
2. Ces vérifications peuvent être utilisées dans la correspondance de modèles (dépendante). Certes, pas dans le cas de cette fonction valid et pas dans le cas d'idris, c'est douloureusement compliqué, et idris est douloureusement terne de sorte que les informations utiles pour les modèles peuvent être extraites de la structure valid . Néanmoins, valid peut être réécrit dans un style de correspondance de motifs légèrement plus convivial, mais cela dépasse le cadre de cet article et n'est généralement pas trivial en soi.

Quels sont les inconvénients?

Je ne vois qu'un seul défaut fondamental grave: la valid est une fonction trop stupide. Il ne renvoie qu'un seul bit d'informations - que les données aient ou non été validées. Dans le cas de types plus intelligents, nous pourrions réaliser quelque chose de plus intéressant.

Par exemple, imaginez que l'exigence d'unicité des adresses ait disparu des savoirs traditionnels. Dans ce cas, il est évident que l'ajout d'une nouvelle adresse à la liste d'adresses existante ne rendra pas la liste invalide, donc nous pourrions prouver ce théorème en écrivant une fonction avec le type So (valid $ types lst) -> So (valid $ types $ addr :: lst) , et l'utiliser, par exemple, pour écrire un type sûr toujours réussi

 insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) 

Mais, hélas, des théorèmes comme la récursivité et l'induction, et notre problème n'a pas de structure inductive élégante, donc, à mon avis, le code avec le chêne booléen valid également bon.