Dans cet article, nous allons créer un modèle de contrôleur basé sur la bibliothèque standard de modélisation structurelle (sans utiliser une bibliothèque prête à l'emploi de blocs de régulation flous).
En tant qu'objet de contrôle, un modèle de moteur à turbine à gaz tiré du manuel de V.I. Gosteva «Régulateurs flous dans les systèmes de contrôle automatique»
Faisons une comparaison avec les régulateurs PID et SDA.
Énoncé du problème
La différence entre un moteur à turbine à gaz (GTE) et un turboréacteur (turboréacteur) est que dans un moteur à turbine à gaz, toute l'énergie est éliminée par l'arbre. Dans les turboréacteurs, l'énergie est libérée sous forme de jet stream.
Les moteurs à turbine à gaz (GTE) sont largement utilisés dans les industries du gaz et de l'aviation, où ils sont à la base des unités de pompage de gaz et des centrales électriques d'aéronefs, dans les entraînements de turbogénérateurs électriques industriels de centrales électriques de pointe et mobiles, dans les centrales marines et autres installations industrielles où le développement de grandes capacités uniques est requis. (de 1 à 25 MW) dans une seule unité avec son poids et ses dimensions minimales.
Un ensemble d'exigences est imposé aux moteurs à turbine à gaz concernant leur fiabilité, leur efficacité énergétique, leur sécurité et leur respect de l'environnement pendant le fonctionnement. Parallèlement à ces exigences, les exigences de qualité des transitoires associées au lancement de l'unité, une forte variation de la charge (puissance) sélectionnée sont pertinentes. À bien des égards, la satisfaction de ces exigences réside dans le système de contrôle automatique (ACS) du moteur à turbine à gaz.
Un moteur à turbine à gaz typique utilisé dans l'industrie est un turbomoteur, dont le circuit est illustré à la figure 1.
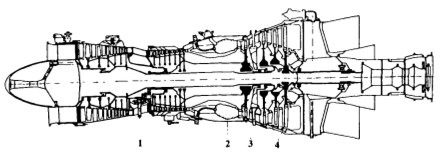
Figure 1. Schéma d'un moteur à turbine à gaz industriel typique:
1- compresseur; 2 - une chambre de combustion; 3 - turbine à compresseur; 4 - turbine de puissance.
Le moteur est une machine rotative dans laquelle l'air est comprimé dans le compresseur 1, le carburant fourni à l'air est brûlé dans la chambre de combustion 2, une partie de l'énergie est prélevée sur les gaz chauds dans la turbine du compresseur 3, consommée par l'entraînement du compresseur 1, 4 gaz dans la turbine de puissance l'expansion crée une puissance prise au moteur par le consommateur.
Dans la grande majorité des moteurs à turbine à gaz, la vitesse du rotor est une quantité contrôlée. En tant que facteur de contrôle dans l'ACS, la vitesse du rotor n est la consommation de carburant GT utilisée dans la chambre de combustion. À différents modes de fonctionnement et dans diverses conditions externes, les paramètres du moteur changent considérablement.
Considérons un moteur à turbine à gaz (GTE) comme un objet de commande instable, pour lequel la vitesse du rotor est n variable contrôlée, et la consommation de carburant G T est l'action de commande. En linéarisant les dépendances du moment de la turbine - M T et du moment du compresseur - M K , sur la vitesse du rotor et sans tenir compte de l'influence de la capacité thermique et massique du moteur pour un mode de fonctionnement particulier, notez la fonction de transfert du moteur comme suit:
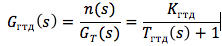
où le gain et la constante de temps sont définis comme:
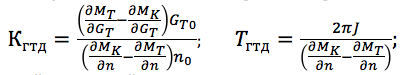
de plus, les signaux d'entrée et de sortie sont enregistrés dans des écarts relatifs sans dimension par rapport à l'état stationnaire (n = Δn / n 0 ; G T = ΔG / G TO , où les valeurs de base des paramètres sont sélectionnées pour un mode de fonctionnement spécifique du moteur, par exemple nominal ou maximal). À différents modes de fonctionnement et dans diverses conditions externes, le gain et la constante de temps du moteur changent considérablement, par conséquent, pour chaque mode, il est nécessaire de déterminer ses propres valeurs de K GTD et T GTD .
Il est à noter que la fonction de transfert G du ou des moteurs à turbine à gaz pour un objet de commande instable, tel qu'un moteur à turbine à gaz, est obtenue par la méthode des coefficients «gelés» sous la condition d'un changement assez lent des paramètres de l'objet.
Le schéma de principe d'un système électromécanique analogique pour contrôler automatiquement la vitesse du rotor d'un moteur est illustré à la figure 2.
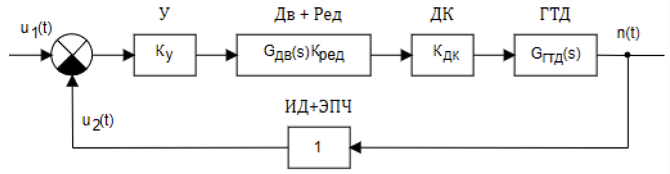
Figure 2. Schéma fonctionnel d'un GTE SAR analogique
La fréquence de rotation est fixée par la tension u 1 (t) et est modifiée par un capteur d'impulsions ID, dont la fréquence du signal de sortie est déterminée par l'expression:
f = kmn, où n est le nombre de tours du moteur, m est le nombre de dents d'engrenage, k est le rapport d'engrenage. La tension alternative prélevée sur la sortie ID à l'aide du convertisseur de fréquence électronique de l'EPC est convertie en un signal u2 (t), dont la valeur est proportionnelle au nombre de tours du moteur - n. La tension u2 (t) est comparée à la tension de référence et au signal d'erreur après que l'amplificateur U est fourni au moteur asynchrone diphasé Dv, qui régule le papillon des gaz DK à travers la boîte de vitesses rouge, modifiant le débit de carburant entrant dans le moteur à turbine à gaz. Un capteur d'impulsions associé à un convertisseur de fréquence électronique peut être décrit par une liaison proportionnelle avec une fonction de transfert égale à l'unité. Dans ce cas, le système lui-même a une seule rétroaction.
En considérant la connexion en série de l'amplificateur, du moteur à induction, de la soupape d'étranglement, de l'unité de turbine à gaz et du capteur de fréquence avec un convertisseur de fréquence électronique comme objet de contrôle commun, et en utilisant un régulateur numérique flou, le schéma fonctionnel complet de la figure 2 peut être réduit au schéma fonctionnel de la figure 3. les fonctions de transfert des liaisons sont réduites à une fonction de transfert commune G 0 (s).
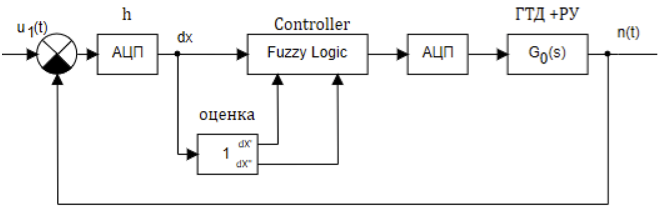
Figure 3. La structure du système de contrôle avec un contrôleur flou.
La fonction de transfert générale G0 (s) peut s'écrire:
G 0 (s) = G (s) K ÉDITER À G (s) = α [s (s + a) (s + b)] -1 , où
α = ab K K EDIT TO K ,
a = 1 / T DW ,
b = 1 / T GTE
Par exemple, nous supposons que les dépendances de la fonction de transfert sur le temps de fonctionnement prennent les valeurs suivantes:
T GTD (t) = 0,9849 - 0,1188 × t + 0,0063 × t 2 - 0,00012 × t 3 ;
α (t) = 16,5475 - 4,4469 × t + 0,4843 × t 2 - 0,02315 × t 3 + 0,0004 × t 4 ;
T DW = 0,35 s.
Dans l'étude du système de commande, nous supposons que la fonction donnée de changement de la vitesse de rotation du rotor d'un moteur à turbine à gaz est définie par la tension d'entrée u (t)
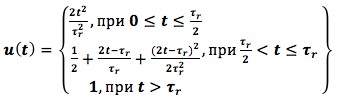
où τ r est le temps d'accélération du moteur. On prend τ r = 6 sec.
Création d'un modèle dynamique
Un modèle simplifié du moteur est présenté à la figure 4. Dans ce modèle, nous utilisons des paramètres variables de blocs typiques qui changent pendant la simulation de la dépendance donnée ci-dessus.
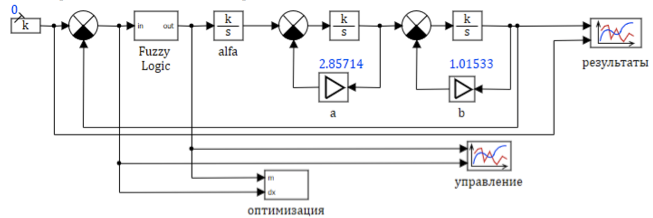
Figure 4. Schéma structurel d'un modèle de moteur à turbine à gaz
Les coefficients des amplificateurs alfa, a, b sont calculés à l'aide d'un langage de script, le texte du programme ci-dessous:
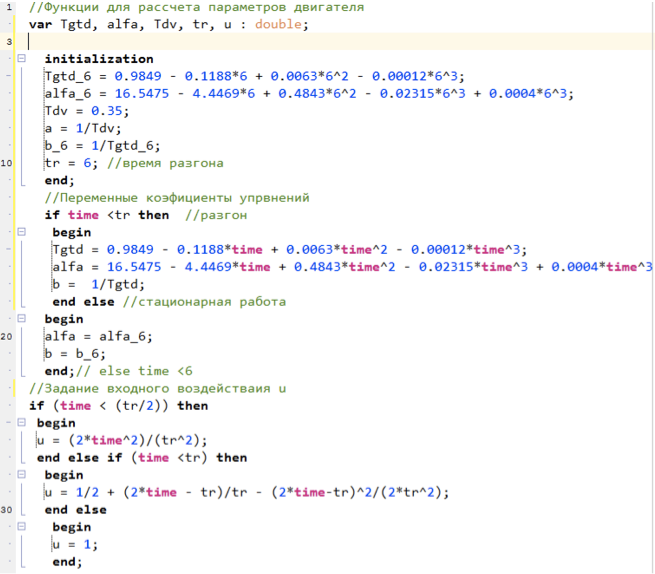
Figure 5. Script de calcul des paramètres du modèle.
Bouton de commande à logique floue
Le régulateur de contrôle prend l'entrée de l'inadéquation entre la valeur définie et la valeur obtenue à partir du modèle, et doit calculer l'action de contrôle.
Essayons d’assembler un contrôleur basé sur une logique floue, en utilisant uniquement des blocs de modélisation structurelle mathématiquement standard, sans utiliser de bibliothèque spécialisée.
Une description des principes de contrôle basés sur la logique floue peut être trouvée dans l' article précédent sur le hub, ou dans la description de la création d'une bibliothèque spécialisée de blocs ici (soigneusement, blasphème).
Tout contrôleur basé sur une logique floue effectue la séquence de transformations suivante:
- Phasage des variables d'entrée. La valeur de la variable est remplacée par un ensemble de termes.
- Activation des conclusions des règles de la logique floue.
- Accumulation de conclusions pour chaque variable linguistique.
- Défazification des variables de sortie.
Pour contrôler le moteur, nous utiliserons trois variables continues, qui sont calculées sur la base d'un signal:
- déviation
- écart dérivé (écart de taux de variation);
- la dérivée seconde de l'écart (accélération des variations des écarts).
Le schéma de calcul est présenté à la figure 6:
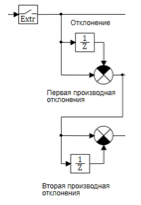
Figure 6. Calculs des écarts de dérivée première et seconde.
Le bloc extrapolateur quantifie le signal entrant dans le contrôleur avec une période de 0,01 s. Les dérivées première et seconde sont calculées à l'aide de formules de différence:
 où:
où:
u (t) est l'écart actuel au temps t;
u (t-Δt) est l'écart à l'instant t - Δt;
u '(t) est la valeur courante de la dérivée de l'écart au temps t;
u '(t-Δt) est la valeur de la dérivée de l'écart à l'instant t - Δt;
u '' (t) est la valeur actuelle de la dérivée seconde de l'écart au temps t;
u '' (t-Δt) est la valeur de la dérivée seconde de l'écart à l'instant t - Δt;
Δt est la période de quantification.
La division par Δt est effectuée dans l'unité de comparaison.
À la suite de ce bloc, trois variables linguistiques sont créées: écart, première variable d'écart, deuxième variable d'écart.
Pour résoudre le problème du contrôle flou, nous n'utiliserons que deux termes pour chaque variable linguistique.
Déviation - moins, plus;
La dérivée première de l'écart diminue, augmente;
La dérivée seconde de la déviation - ralentit, accélère.
Pour calculer la valeur de la fonction d'appartenance μ pour chaque terme, nous utilisons une fonction linéaire avec saturation. Cette fonction pour le terme est supérieure à 0 lorsque la valeur d'entrée est minimale et 1 lorsque la valeur d'entrée est maximale. Pour un terme inférieur, cette fonction prend la valeur 1 lorsque la variable est égale au minimum et 0 lorsque la variable est maximale. (voir fig.7)
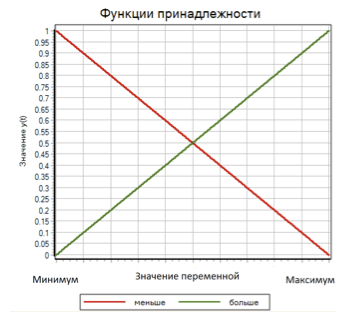
Figure 7. Fonctions d'adhésion pour les termes de moins en plus.
Ainsi, pour chacune des trois variables d'entrée (écart, première dérivée de l'écart, deuxième dérivée de l'écart), il y a plus ou moins deux termes, la valeur des fonctions d'appartenance μ i qui varient linéairement de 0 à 1 en fonction de la valeur de l'entrée variable.
En tant que variable linguistique de sortie, nous utilisons l'effet de sortie, qui n'a également que deux termes pour réduire et augmenter.
D'après le schéma du modèle de la Fig. 4 il est évident que si l'écart est inférieur à 0, alors la valeur est supérieure à la valeur spécifiée et doit être réduite. Si l'écart est supérieur à 0, la fonction est inférieure à celle spécifiée et doit être augmentée.
Les règles logiques des deux termes ressembleront à ceci:
- Si moins et diminue et ralentit => diminuer.
- Si plus et augmente et accélère => augmenter.
Pour activer les règles d'inférence floue, nous utilisons la fonction minimum pour l'opérateur flou et l'opérateur. La valeur des fonctions d'appartenance pour les termes de la fonction de sortie est calculée par les formules:
μ
diminution = MIN (μ
moins , μ
diminue , μ
ralentit )
μ
augmentation = MIN (μ
plus , μ
augmente , μ
accélère )
Pour assurer la conversion des termes en valeurs d'impact spécifiques (accumulation et dénazification), nous utilisons l'algorithme de Tsukamoto comme centre de gravité des points.
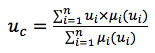 où
où
u c est la fonction résultante;
u i est la valeur de la fonction pour le terme i;
μ i est la valeur de la fonction d'appartenance pour les termes de la fonction.
Dans notre cas, la fonction résultante pour deux termes est calculée par la formule:
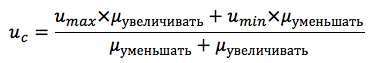
Le schéma général de l'algorithme d'inférence floue est présenté à la figure 8:
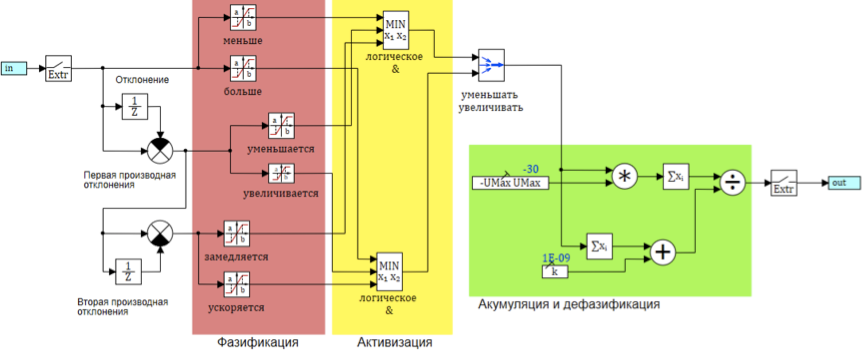
Figure 8. Schéma de l'algorithme d'inférence floue
Pour que cet algorithme fonctionne, nous devons définir les valeurs minimum et maximum pour 6 termes de trois variables linguistiques (déviation, 1ère dérivée de la déviation, 2e dérivée de la déviation). Pour réduire les calculs, nous supposons que l'écart est symétrique par rapport à zéro. Il nous suffit ensuite de trouver 3 valeurs absolues, une pour chaque variable.
deltMax - écart maximum. Définit les valeurs des termes less, more (-deltMax, deltaMax);
divMax est la dérivée maximale de l'écart. Définit les valeurs des termes diminue, augmente (-divMax, divMax);
div2Max est la dérivée seconde maximale. Définit les valeurs des termes ralentit, accélère (-div2Max, div2Max).
Les effets maximum et minimum de umin et umax sont déterminés par les caractéristiques de conception et dans cet exemple sont pris égaux à +30 et -30.
Réglage du contrôleur par optimisation.
Pour sélectionner les coefficients, nous utilisons le même schéma d'optimisation que nous avons utilisé dans les expériences précédentes avec la logique floue.
Comme critère d'optimisation, nous prenons l'écart type de pas plus de 0,001 et le nombre de commutations dans l'unité de contrôle pas plus de 25. Pour la commutation, nous prenons un changement dans le signe de l'action de contrôle.
Le circuit du bloc de paramètres du contrôleur est illustré à la Fig. 9.
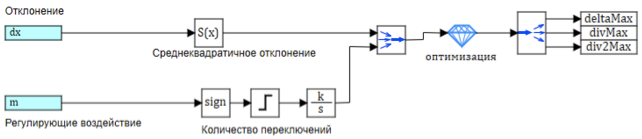
Figure 9. Configuration des paramètres de sortie floue.
À la suite de l'opération de blocage, les paramètres suivants ont été obtenus
deltMax = 0,00746;
divMax = 0,2657;
div2Max = 25,13;
Les résultats de la transition sont présentés à la figure 10.
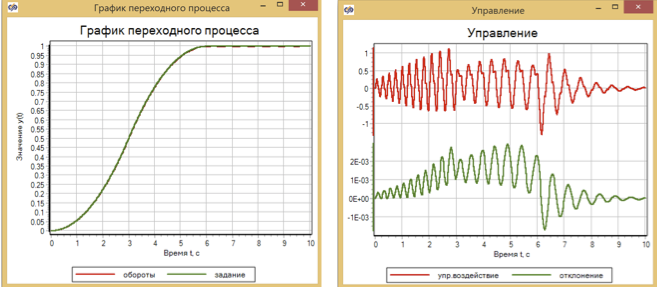
Figure 10. Contrôle transitoire et moteur en utilisant la logique floue.
L'écart maximal des révolutions par rapport à l'ensemble après optimisation était de 2,5 × 10 -3 . Ce qui, en principe, n'est pas mauvais, mais dans le livre de V.I. Les écarts des invités dans le modèle après les réglages étaient inférieurs de deux ordres de grandeur: le maximum était de 5 × 10 -5 .
A titre de comparaison, nous présentons les résultats du fonctionnement du contrôleur PID Fig. 11 et les règles de trafic Fig. 12 pour le même modèle de moteur simplifié. Les paramètres de ces régulateurs ont également été sélectionnés par la méthode d'optimisation.
Par conséquent, un écart plus important est obtenu pour le contrôleur PID que pour un contrôleur basé sur une logique floue - environ 6 × 10 -3 , et pour un contrôleur de trafic qui utilise la dérivée seconde, l'écart est d'environ 3 × 10 -3 (voir 13). De plus, sur tous les graphiques, on peut voir que lorsque l'impact spécifié change (changements dans les sections 3 sec, 6 sec), la qualité de la régulation change.
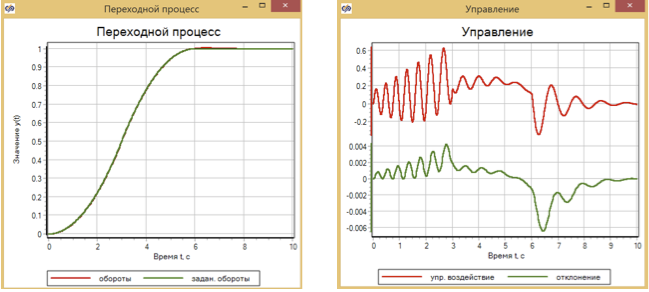
Figure 11. Contrôle transitoire et moteur à l'aide d'un contrôleur PID.
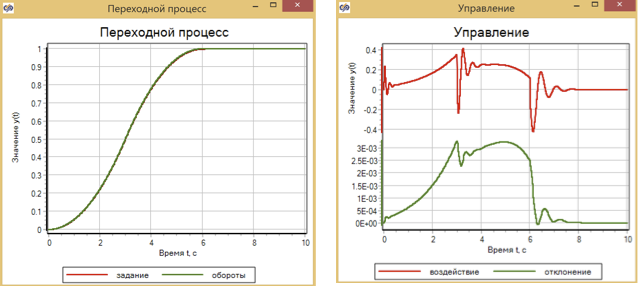
Figure 12. Processus transitoire et contrôle du moteur à l'aide du contrôleur de la circulation.
Pour démarrer le moteur, la fonction de transition est utilisée sous la forme d'un changement de vitesse en douceur. Nous avons également réglé les régulateurs par la méthode d'optimisation pour un contrôle optimal selon cette loi. Essayons d'appliquer un effet pas à pas et voyons comment les régulateurs, initialement optimisés pour un processus de transition en douceur, peuvent faire face.
En effet, nous utilisons une étape de 0 à 1 à 3 secondes du processus.
Les résultats de l'expérience sont présentés dans les figures 13-15.
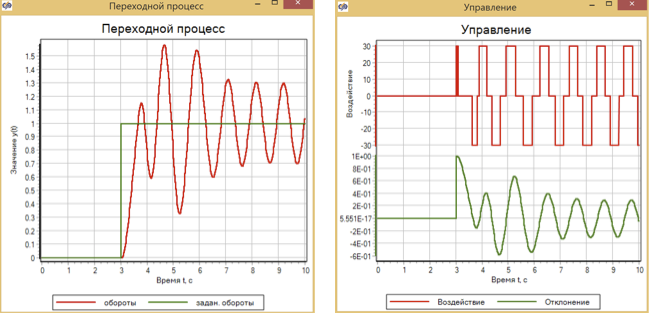
Figure 13. Processus transitoire et contrôle avec une action de contrôle pas à pas avec un contrôleur à logique floue.
On peut voir qu'un régulateur réglé pour une accélération en douceur du moteur ne gère pas le contrôle pendant une action pas à pas, et le système entre en mode d'auto-oscillation.
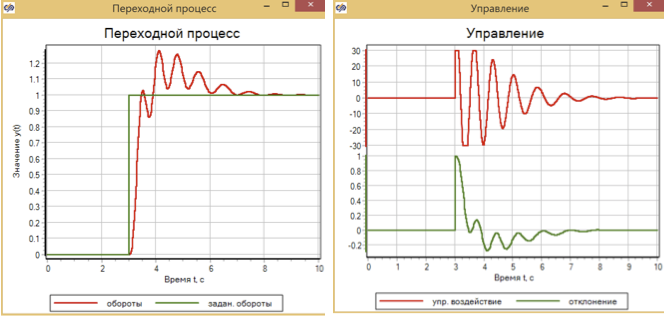
Figure 14. Processus transitoire et contrôle avec action de contrôle par étapes avec contrôleur PID.
Un contrôleur PID réglé sur un processus fluide, avec un effet pas à pas, fournit une transition vers un temps prédéterminé, mais en même temps, il y a un dépassement de 30% et un processus oscillatoire en 4 secondes.
Le contrôleur de trafic, configuré pour une régulation en douceur, avec un effet pas à pas fournit une transition en douceur sans dépassement (Fig.14)
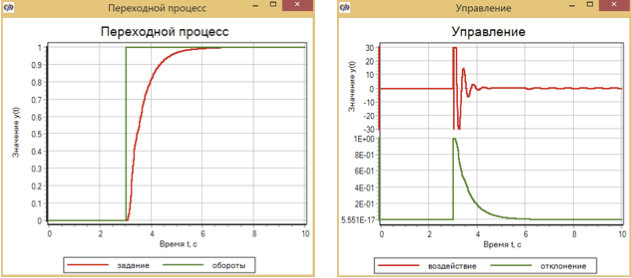
Figure 15. Processus de transition et contrôle avec une action de contrôle par étapes avec un contrôleur de trafic.
Conclusions
Ces expériences numériques ont montré qu'un contrôleur basé sur une logique floue fournit un contrôle plus précis des révolutions d'un modèle de moteur simple avec un changement en douceur de la valeur définie que le PID et le SDA.
Cependant, un tel réglage, comme il s'est avéré, ne garantit pas la stabilité du régulateur lors d'une action pas à pas.
Dans le même temps, pour un modèle simplifié du moteur, un contrôleur basé sur une logique floue dans le cas d'une action pas à pas s'est avéré pire qu'un contrôleur PID ou SDA.
Lien vers l'archive avec les projets de l'article d'autoformation