Présentation
Quatre mois se sont écoulés depuis la publication de l'article sur ma tentative d'implémentation de bas niveau de l'
arborescence des préfixes . Malgré tous mes efforts, le plafond sur lequel ma mise en œuvre précédente de l'arborescence des préfixes s'est avéré être d'environ 80 000 mots par seconde. J'ai ensuite passé beaucoup de temps et d'énergie, mais le résultat ne conviendrait que comme travail de laboratoire en informatique.
Beaucoup m'ont alors dit: «N'inventez pas un vélo que nous avons déjà inventé! Utilisez la solution clé en main. " La difficulté est que je ne pouvais pas utiliser quelque chose que je ne comprends pas au moins en termes généraux.
Je pense avoir compris l'arborescence des préfixes, et c'est ce que j'ai réussi à réaliser.
Principe de fonctionnement
Je ne connais pas très bien l'anglais, donc parmi les nombreux articles que j'ai lus sur le thème des arborescences de préfixes, certaines informations ne m'ont probablement pas atteint. Par conséquent, j'ai trouvé comment tout arranger, en ne comprenant que le principe de base de l'arbre des préfixes. Pour ceux qui ne le savent pas, je vais essayer de le décrire plus clairement qu'il n'est écrit sur Wikipédia. J'ai donc expliqué ce que je faisais à ma femme.
L'arbre des préfixes est une structure logique pour stocker des données qui peuvent être représentées comme un index de cartes de livres dans une bibliothèque. Chaque case a un numéro. Chaque case correspond à une lettre spécifique de l'alphabet. A l'intérieur se trouvent les numéros des tiroirs suivants, ouverture que vous pouvez découvrir les suivants et ainsi de suite. Quand il n'y a rien à l'intérieur de la boîte, cela signifie que la lettre de cette boîte est la dernière du mot. Le problème est que certaines cases restent presque vides, car elles contiennent 1 ou 2 chiffres, et l'espace restant est vide.
Pour résoudre ce problème, de nombreuses variétés d'arbres de préfixes sont apparues, y compris: HAT-trie, double-array trie, tripple-array trie. C'est précisément le fait que je n'ai pas pu comprendre à fond le principe de leur travail qui m'a poussé à un arbre aussi simple qu'un fichier de carte de bibliothèque.
La dernière fois, j'ai réussi à implémenter une implémentation de consommation de mémoire plutôt économique d'un simple arbre de préfixe. Poursuivant cette métaphore avec un classeur de bibliothèque, j'ai fait des tiroirs dans mon classeur de différentes tailles, pour l'alphabet complet la boîte est la plus grande, pour 1 lettre la plus petite.
J'ai réussi à implémenter exactement le même schéma PHP en C.
1. Chaque lettre du mot selon le tableau établi est codée avec un nombre de 2 à 95. Par exemple, le mot «abv» est codé avec trois nombres: 11, 12, 13. Pour des performances maximales, un tableau bidimensionnel de nombres de 1 octet de
uint8_t abc[256][256] = {}; Pour convertir un programme, il lit une ligne d'un octet, il essaie de prendre la valeur de chaque octet de notre tableau. Par exemple, le code numérique est 1 = 49, donc nous regardons
abc[49][0]; . S'il y a une valeur autre que '\ 0', alors c'est le code de notre lettre, souvenez-vous-en et passez à l'octet suivant. Dans notre cas, le mot «abv» consiste en une séquence de 6 octets, deux octets par lettre: 208, 176, 208, 177, 208, 178. Puisque le codage utf-8 est conçu pour que les premiers octets de caractères à un octet ne coïncident jamais avec les premiers octets de plusieurs octets , dans notre tableau
abc[208][0] = 0; .
Cependant, pour les paires d'octets, il existe des correspondances:
/* [11] */ abc[208][176] = 11; /* [12] */ abc[208][177] = 12; /* [13] */ abc[208][178] = 13;
2. Maintenant, nous devons noter les nombres 11, 12 et 13 dans les cases de notre arbre. L'arbre se compose de 2 blocs de mémoire non explosifs séparés, le premier est un bloc de nœuds, le second est un bloc de liens, ainsi que deux compteurs de nœuds occupés et des cellules occupées d'un bloc de liens. Chaque nœud d'arborescence se compose de 16 octets, 12 octets d'un masque de bits et 4 octets pour stocker l'ID du bloc de liaison. Le masque vous permet de stocker des nombres de 2 à 96 bits. Le premier bit du masque est utilisé pour marquer la fin du mot sur ce nœud. Chaque nœud peut correspondre à l'id du bloc de liaison si au moins 1 lettre est écrite dans ce nœud, ou ne pas correspondre si le nœud est une «feuille» en termes d'arbres, c'est-à-dire qu'un mot se termine simplement dessus. Exprimé dans une bibliothèque, un tiroir vide.
3. Prenez le masque du premier nœud (racine). trie-> nœuds [0] .mask; Nous comptons les bits levés dans ce masque, à partir du second (le premier pour le drapeau de fin de mot). Si aucun bit du masque n'est relevé, c'est-à-dire Étant donné que le nœud est vide, nous avons besoin d'un bloc de liens de taille 1 pour stocker notre numéro 11, prenez le numéro du compteur de références de liens du bloc et augmentez l'ancienne valeur d'un (car nous avons besoin de la taille 1). Nous prenons le nombre du compteur de nœuds et augmentons également l'ancienne valeur de 1. Nous écrivons l'ID du bloc de liens, qui est le nombre obtenu du compteur de blocs de liens, dans notre nœud racine. Et dans cet identifiant du bloc de liaison, écrivez l'identifiant du nouveau nœud, c'est-à-dire le nombre obtenu à partir du compteur de nœuds. Maintenant, en plus du nœud racine (id 0), nous avons un nœud de la lettre «a» (id 1). Pour écrire le nombre 12 correspondant à la lettre «b», on fait de même, mais avec le nœud de la lettre «a».
4. Sur la dernière lettre «c», nous n'avons pas besoin de place dans le bloc de liens, car nous aurons le dernier nœud sur la branche ou la feuille de nœud. Un tel nœud n'a que 1 bit dans le masque relevé.
5. La partie la plus difficile du travail d'un arbre se produit lorsqu'il est écrit dans un nœud dans lequel certaines lettres ont déjà été écrites. Dans ce cas, le schéma de fonctionnement est le suivant:
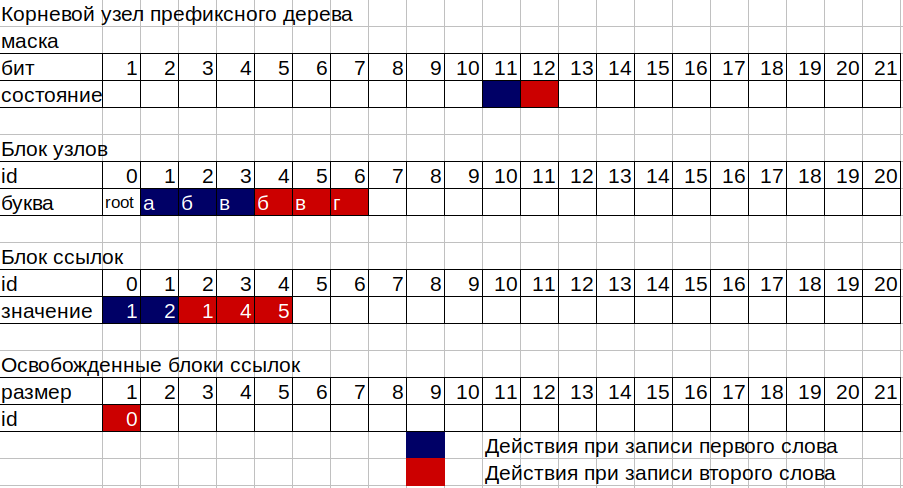
Supposons que nous voulions ajouter le mot «bvg» (12, 13, 14) à notre arbre, dans lequel le mot «abv» (11, 12, 13) est déjà écrit. Nous comptons les bits du masque du nœud racine jusqu'au bit de la lettre qui nous intéresse. Nous avons la lettre «b» avec le code 12, ce qui signifie que le bit de cette lettre est 12, dans le masque de 1 à 12 bits le bit 11 de la lettre «a» a déjà été soulevé. Nous avons donc la taille actuelle du bloc de liens pour le nœud racine 1. Nous écrivons la deuxième lettre, nous avons donc maintenant besoin d'un bloc de liens de taille 2. Ici, le registre des blocs libérés entre en jeu, dans lequel l'id et la taille des sections du bloc de liens ne sont plus utilisés par les nœuds arbre. Notre ancien identifiant du bloc de liaison pour le nœud racine de taille 1 vient juste d'entrer dans le registre des sections libres de taille 1, car notre nœud racine a besoin d'une plus grande taille. Notre registre n'a pas de section appropriée de taille 2 et nous prenons à nouveau la valeur du compteur du bloc de liaison comme nouvel identifiant du bloc de liaison, augmentant le compteur de 2. À la nouvelle adresse du bloc de liaison dans le même ordre dans lequel les bits sont situés dans le masque de nœud, nous écrivons la valeur id noeud de l'ancien bloc de liens pour la lettre "a" du premier mot et la valeur du noeud qui vient d'être créé de la lettre "b" du second mot.
Vitesse de travail
Le roulement de tambour sonne ... Vous vous souvenez du dernier résultat? Environ 80 mille mots par seconde. L'arbre a été créé à partir du dictionnaire de tous les mots russes OpenCorpora 3 039 982 mots. Et voici ce qui s'est passé maintenant:
yatrie creation time: 4.588216s (666k wps) yatrie search time 1 mln. rounds: 0.565618s (1.76m wps)
MISE À JOUR 11/01/2018:Dans la version 0.0.2, il était possible d'augmenter la vitesse de près de 2 fois en remplaçant les fonctions à part entière par des fonctions macro, ainsi qu'en changeant la structure du masque de nœud en masque uint32_t [3], auparavant c'était le masque uint8_t [12].
Ajout de macros LIKELY () UNLIKELY () pour prédire les résultats attendus dans ces blocs if (), si possible.
MISE À JOUR 11/05/2018:Tordu un peu plus. J'ai réussi à le faire fonctionner correctement même lors de la compilation de -O3 et -Ofast. La vitesse de recherche dans l'arbre est de ~ 0,2 μs ou 0,2c pour 1 million de répétitions. Apparemment, cette vitesse a été obtenue en raison de la transition vers un format différent du masque. Auparavant, il y avait 12 octets de 8 bits, et maintenant 3 int32 et une fonction très rapide pour compter les bits en int32.
Est-ce compact?
Le dictionnaire OpenCorpora spécifié prend ~ 84 Mo, ce qui n'est pas bien pire que libdatrie, qui donne ~ 80 Mo.
→
Code sourceBienvenue