➡️ 👽 🌓 Implémentation de l'algorithme de Levenberg-Marquardt pour l'optimisation des réseaux de neurones sur TensorFlow 👨🏼‍🚒 👨🏽‍🎨 👩🏾‍💼

Il s'agit d'un didacticiel de la bibliothèque TensorFlow. Considérez-le un peu plus profondément que dans les articles sur la reconnaissance des nombres manuscrits. Ceci est un tutoriel sur les méthodes d'optimisation. Ici, vous ne pouvez pas vous passer des mathématiques. Ce n'est pas grave si vous l'avez complètement oublié. Rappel. Il n'y aura pas de preuves formelles et de conclusions complexes, seulement le minimum nécessaire pour une compréhension intuitive. Pour commencer, un petit aperçu de la façon dont cet algorithme peut être utile pour optimiser un réseau de neurones.

Il y a six mois, un ami m'a demandé de montrer comment créer un réseau neuronal en Python. Sa société produit des instruments de mesures géophysiques. Plusieurs sondes différentes lors du forage mesurent un ensemble de signaux associés aux paramètres de l'environnement entourant le puits. Dans certains cas complexes, calculez avec précision les paramètres environnementaux à partir de signaux pendant une longue période, même sur un ordinateur puissant, et il est nécessaire d'interpréter les résultats de mesure sur le terrain. Il y avait une idée de compter plusieurs centaines de milliers de cas sur un cluster, et de former un réseau neuronal sur eux. Le réseau neuronal étant très rapide, il peut être utilisé pour déterminer des paramètres cohérents avec les signaux mesurés, en plein processus de forage. Les détails sont dans l'article:

Kushnir, D., Velker, N., Bondarenko, A., Dyatlov, G., et Dashevsky, Y. (2018, 29 octobre). Simulation en temps réel de l'outil de résistivité azimutale profonde dans un modèle de défaut 2D à l'aide de réseaux de neurones (russe). Société des ingénieurs pétroliers. doi: 10.2118 / 192573-RU

Un soir, j'ai montré comment les keras pouvaient implémenter un réseau neuronal simple, et un ami au travail a commencé à s'entraîner sur les données comptées. Après quelques jours, nous avons discuté du résultat. De mon point de vue, il avait l'air prometteur, mais un ami a dit qu'il avait besoin de calculs avec la précision de l'appareil. Et si l' erreur quadratique moyenne s'est avérée être d'environ 1, alors 1e-3 était nécessaire. 3 commandes de moins. Mille fois.

Les expériences avec l'architecture des réseaux de neurones, la normalisation des données et les approches d'optimisation n'ont donné presque rien. Quelques semaines plus tard, un ami a appelé et a dit qu'il avait installé MatLab et avait résolu le problème par la méthode Levenberg-Marquardt (ci-après nous appellerons LM ). Il a été optimisé pendant longtemps (plusieurs jours), il n'a pas fonctionné sur le GPU, mais le résultat était le bon. Cela ressemblait à un défi.

Une recherche rapide d'un optimiseur LM prêt à l'emploi pour les kéros ou TensorFlow a échoué. Je ne suis tombé que sur la bibliothèque pyrenn, mais sa fonctionnalité me semblait médiocre. J'ai décidé de le mettre en œuvre moi-même. À première vue, tout avait l'air simple et deux soirées auraient dû suffire. Cela a pris plus de temps. Il y avait deux problèmes:

TensorFlow. Un tas d'articles, mais presque tous les niveaux "mais écrivons ~~bonjour la~~ reconnaissance des chiffres manuscrits du ~~monde~~ ."
Math J'ai beaucoup oublié, et les auteurs d'articles mathématiques ne se soucient pas du tout de gens comme moi: des formules solides sans explication, "évidemment!" et ainsi de suite.

En conséquence, il a écrit un article pour ceux qui ont oublié les mathématiques et veulent comprendre TensorFlow un peu plus profondément, mais sans hardcore. L'article contient beaucoup de texte et peu de code. L'option opposée, lorsqu'il y a peu de texte et beaucoup de code, est ici Jupyter Notebook Levenberg-Marquardt .

Découvrez la fonction Rosenbrock

Nous générerons des données d'entraînement par la fonction Rosenbrock , qui est souvent utilisée comme référence pour les algorithmes d'optimisation:

$f (x, y) = (a-x) ^ 2 + b (y-x ^ 2) ^ 2$

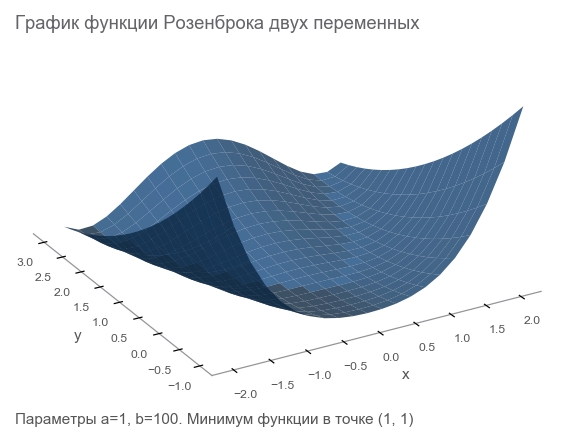
Pourquoi est-elle bonne?

Beau programme. On l'appelle la vallée de Rosenbrock et la fonction banane de Rosenbrock intraduisible.
Le minimum global se situe à l'intérieur d'une longue vallée plate parabolique et étroite. Trouver une vallée est trivial et un minimum global est difficile.
Il existe une option multidimensionnelle. Trouver une bonne fonction pour de nombreuses variables n'est pas si simple.

Nous allons commencer à en écrire du code en connectant les bibliothèques nécessaires à la poursuite des travaux:

import numpy as np import tensorflow as tf import math def rosenbrock(x, y, a, b): return (a - x)**2 + b*(y - x**2)**2

Nous énonçons le problème

Puisque nous parlions d'un appareil de mesure, continuons à utiliser l'analogie. Notre appareil dans un monde fictif peut mesurer des coordonnées $(x, y)$ et hauteur $z$ . Les physiciens ont étudié le monde et ont dit: " Oui, c'est Rosenbrock! Connaissant les coordonnées, vous pouvez calculer avec précision la hauteur, vous n'avez pas besoin de la mesurer. ". En d'autres termes, les scientifiques nous ont donné un modèle $z = rosier (x, y, a, b)$ qui dépend des paramètres $(a, b)$ . Ces paramètres, bien que constants dans un monde fictif, sont inconnus. Ils doivent être trouvés.

Nous avons mené une série d'expériences qui ont donné $m$ des points $(x_1, y_1, z_1), (x_2, y_2, z_2), ..., (x_m, y_m, z_m)$ :

 # (2.5, 2.5) -   ,  ,     data_points = np.array([[x, y, rosenbrock(x, y, 2.5, 2.5)] for x in np.arange(-2, 2.1, 2) for y in np.arange(-2, 2.1, 2)]) m = data_points.shape[0]

La première façon d'optimiser est d'essayer de deviner les paramètres. Nous utilisons la bibliothèque Numpy:

 x, y = data_points[:, 0], data_points[:, 1] z = data_points[:, 2] #   =5  b=5? a_guess, b_guess = 5., 5. #  -hat   ,   , #   ,   ,   .   #     ^   - # .    hat. z_hat = rosenbrock(x, y, a_guess, b_guess)

Comment comprendre à quel point nous avons tort? Compter les résidus - tailles d'erreur. $m$ les points donnent $m$ résidus - vous avez besoin d'un indicateur intégré. Nous plaçons chaque résidu dans un carré et calculons la moyenne:

$MSE (a, b) = \ frac {1} {m} \ sum_ {i = 1} ^ {m} (z_ {i} - \ widehat {z_ {i}}) ^ 2$

Cette mesure de proximité est appelée l' erreur quadratique moyenne (ci-après dénommée mse ):

 # r - residuals () r = z - z_hat # mse loss = np.mean(r**2) print(loss)

 [Out]: 3868.2291666666665

En minimisant mse , nous résolvons le problème des moindres carrés ( minimisation des carrés non linéaires ):

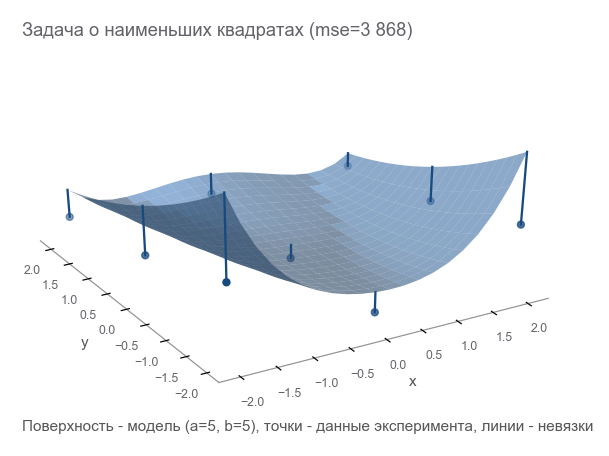
On peut voir que les paramètres ne devinaient pas du tout.

Nous formulons le problème sur TensorFlow

Le modèle a la forme $z = rosier (x, y, a, b)$ . Nous le portons au formulaire $y = f (x, p)$ (généralement les maths écrivent $\ beta$ au lieu de $p$ mais les programmeurs n'utilisent pas la version bêta). Maintenant, le modèle a la forme $y = rosier (x, p)$ où $y$ - hauteur $x$ Est le vecteur de coordonnées de deux éléments (composant), et $p$ - vecteur de paramètres.

Les programmeurs considèrent souvent les vecteurs comme des tableaux unidimensionnels. Ce n'est pas tout à fait correct. Un tableau de nombres est un moyen de représenter un vecteur. Vous pouvez représenter un vecteur comme un tableau de dimension $N$ , tableau bidimensionnel $1 \ fois N$ , et même un tableau $N \ fois 1$ dans les cas où le fait que le vecteur soit un vecteur colonne (par exemple, pour multiplier une matrice par lui) est important:

$\ begin {bmatrix} x_1 \\\ vdots \\ x_N \ end {bmatrix}$

TensorFlow utilise le concept de tenseur . Un tenseur , comme un tableau, peut être unidimensionnel (pour représenter un vecteur ), bidimensionnel (pour un vecteur de matrice ou de colonne ) et n'importe quelle dimension plus grande.

 #    ('placeholder' ,    #      ) x = tf.placeholder(tf.float64, shape=[m, 2]) y = tf.placeholder(tf.float64, shape=[m]) #   ('variable' ,    ) #     (5, 5) p = tf.Variable([5., 5.], dtype=tf.float64) #  y_hat = rosenbrock(x[:, 0], x[:, 1], p[0], p[1]) #  r = y - y_hat # mse (mean squared error) loss = tf.reduce_mean(r**2)

Le code TensorFlow n'est pas différent dans sa forme du code Numpy. Le contenu est énorme. Le code Numpy calcule la valeur mse. Le code TensorFlow n'effectue aucun calcul, il forme un graphique de flux de données que mse peut calculer . Un moment très tolérant au cerveau est le travail de la fonction rosenbrock . Nous l'utilisons dans les deux cas. Mais lorsque nous passons les tableaux Numpy, il effectue les calculs selon la formule et renvoie les nombres. Et lorsque nous transférons les tenseurs vers TensorFlow, il forme un sous - graphique du flux de données et renvoie son bord sous la forme d'un tenseur. Miracles du polymorphisme, mais n'en abusez pas:

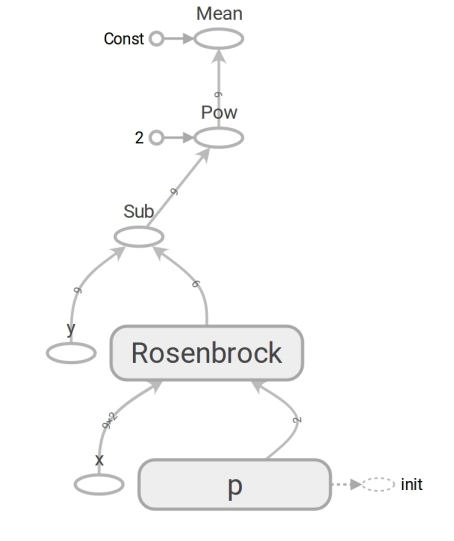
Grâce à la présence d'un tel graphe de flux de données, TensorFlow en particulier est capable de calculer automatiquement des dérivées (en utilisant la technique de différenciation automatique en mode inverse ).

Un moment de maths. Les blocs "pour ceux qui ont oublié" seront cachés dans un spoiler.

Dérivée (nombre entré - nombre restant)

Vous vous souvenez très probablement de la définition de la dérivée d'une fonction scalaire (renvoyant un nombre) d'une variable: pour $f: \ mathbb {R} \ rightarrow \ mathbb {R}$ dérivé $f$ au point $x \ in \ mathbb {R}$ défini comme:

${f} '(x) = \ lim_ {h \ to 0} \ frac {f (x + h) -f (x)} {h}$

Les dérivés sont un moyen de mesurer le changement . Dans le cas scalaire, la dérivée montre à quel point la fonction va changer $f$ si $x$ passer à une petite valeur $\ varepsilon$ :

$f (x + \ varepsilon) \ environ f (x) + \ varepsilon {f} '(x)$

Pour plus de commodité, nous désignons $y = f (x)$ et le dérivé $y$ par $x$ nous écrirons comment $\ frac {\ partial y} {\ partial x}$ . Un tel dossier souligne que $\ frac {\ partial y} {\ partial x}$ - taux de variation entre les variables $x$ et $y$ . Plus précisément, si $x$ changer pour $\ varepsilon$ alors $y$ passer à environ $\ varepsilon \ frac {\ partial y} {\ partial x}$ . Vous pouvez également l'écrire comme ceci:

$x \ rightarrow x + \ Delta x \ Rightarrow y \ rightarrow \ approx y + \ frac {\ partial y} {\ partial x} \ Delta x$

Lit comme: "changer $x$ sur $x + \ Delta x$ changer $y$ à environ $y + \ Delta x \ frac {\ partial y} {\ partial x}$ ". Un tel record met clairement en évidence le lien entre le changement $x$ et changer $y$ .

Nous avons construit un graphique de flux de données, exécutons le calcul mse:

 #        #      placeholder (  ) feed_dict = {x: data_points[:,0:2], y: data_points[:,2]} #       TensorFlow session = tf.Session() #     session.run(tf.global_variables_initializer()) #   ()  loss (mse) current_loss = session.run(loss, feed_dict) print(current_loss)

 [Out]: 3868.2291666666665

Le résultat est le même qu'avec Numpy. Ils ne se sont donc pas trompés.

Commencez à optimiser

Malheureusement, il n'a pas été possible de deviner les paramètres. Mais alors nous:

Nous fixons le critère d'optimalité - la valeur minimale de mse.
Des paramètres variables ont été déterminés: vecteur $p$ avec composants $a$ , $b$ Fonctions de Rosenbrock.
Nous n'avons pas encore pensé aux limitations, mais elles ne sont pas là.

Dans la dernière étape, nous avons construit un graphe de flux de données avec un tenseur de perte finie ( fonction de perte ). Le but de l'optimisation est de trouver la valeur du vecteur paramètre $p$ à laquelle la valeur de la fonction de perte est minimale. Nous avons eu de la chance, le graphe de cette fonction est très simple (concave et sans minima local):

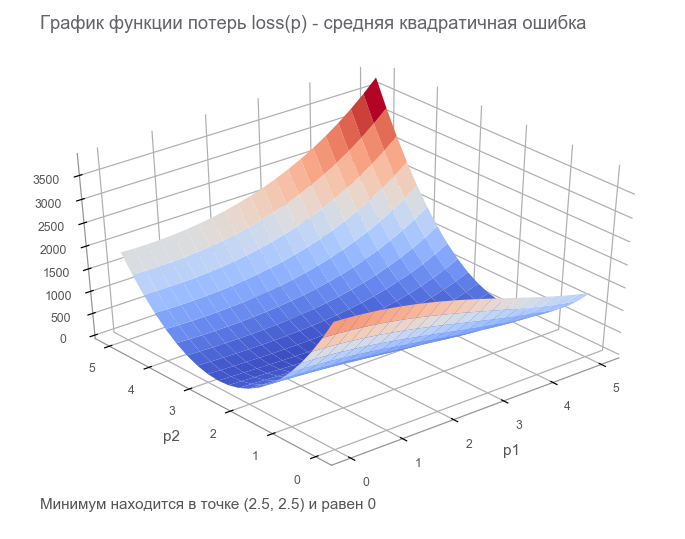
Débuter avec l'optimisation. Pour commencer, nous écrivons un cycle généralisé:

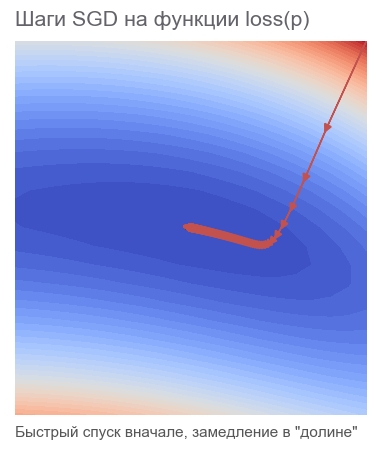
 # :   mse,   ,  #   mse,        placeholder def train(target_loss, max_steps, loss_tensor, train_step_op, inputs): step = 0 current_loss = session.run(loss_tensor, inputs) #           while current_loss > target_loss and step < max_steps: step += 1 #    1, 2, 4, 8, 16...  if math.log(step, 2).is_integer(): print(f'step: {step}, current loss: {current_loss}') #    session.run(train_step_op, inputs) current_loss = session.run(loss_tensor, inputs) print(f'ENDED ON STEP: {step}, FINAL LOSS: {current_loss}')

Nous optimisons par la méthode de la descente de gradient la plus rapide (SGD)

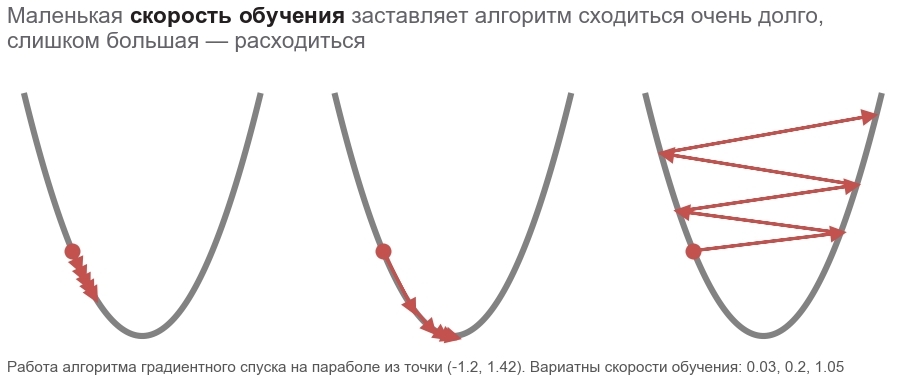
Les actions de cette méthode peuvent être comparées à la conduite d'un skieur audacieux, qui descend toujours la pente (dans la direction la plus raide). Dans ce cas, seule la pente au point de localisation est prise en compte. Et si la pente est forte, le skieur vole sur une longue distance avant le prochain changement. Avec une faible pente, il se déplace par petites étapes. Peut-être comment s'envoler ~~dans un arbre~~ (l' algorithme diverge ), et se coincer dans une fosse ( minimum local ).

Vous pouvez écrire comme suit (changer $\ boldsymbol {p}$ sur $\ boldsymbol {p} - ...$ ):

$\ boldsymbol {p} \ rightarrow \ boldsymbol {p} - \ alpha [\ nabla_ {p} perte (\ boldsymbol {p})]$

Grasse $\ boldsymbol {p}$ souligne qu'il s'agit du point de localisation réel - la valeur du vecteur de paramètre à l'étape actuelle. À la première étape, c'est notre supposition (5, 5). Il y a deux points intéressants dans la formule: $\ alpha$ - taux d'apprentissage ( taux d'apprentissage ), $\ nabla_ {p} perte$ - gradient ( gradient ) de la fonction de perte par le vecteur de paramètres.

Dégradé (vecteur entré - nombre à gauche)

Considérons une fonction qui prend un vecteur en entrée et produit un scalaire: $f: \ mathbb {R} ^ {N} \ rightarrow \ mathbb {R}$ . Dérivé $f$ au point $x \ in \ mathbb {R} ^ {N}$ maintenant appelé gradient et est un vecteur $[\ nabla_ {x} f (x)] \ in \ mathbb {R} ^ {N}$ (lu comme "nabla") composé de dérivées partielles :

$\ nabla_ {x} y = (\ frac {\ partial y} {\ partial x_ {1}}, \ frac {\ partial y} {\ partial x_ {2}}, ..., \ frac {\ partial y} {\ partiel x_ {N}})$

Pour ce cas, l'enregistrement de la dépendance du changement de fonction sur le changement d'argument a la forme suivante:

$x \ rightarrow x + \ Delta x \ Rightarrow y \ rightarrow \ approx y + \ nabla_ {x} y \ cdot \ Delta x$

Le dossier a beaucoup changé pour tenir compte du fait que $x$ , $\ Delta x$ et $\ nabla_ {x} y$ - vecteurs en $\ mathbb {R} ^ {N}$ et $y$ - scalaire. Lors de la multiplication des vecteurs $\ nabla_ {x} y$ et $\ Delta x$ le produit scalaire est utilisé (la somme des produits des composants).

 #        grad = tf.gradients(loss, p)[0] #   learning_rate = 0.0005 #   ,     apply_gradients - #         opt = tf.train.GradientDescentOptimizer(learning_rate=1) #           sgd = opt.apply_gradients([(learning_rate*grad, p)]) #   ,    40000  session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, sgd, feed_dict) print('PARAMETERS:', session.run(p))

 [Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 1381.5379689135807 [...] ENDED ON STEP: 582, FINAL LOSS: 9.698531012270816e-11 PARAMETERS: [2.50000205 2.49999959]

Il a fallu 582 étapes:

Mouvement dans le sens de l'anti-gradient

Pourquoi allons-nous dans la direction opposée au gradient? Rappelez l'entrée avec le produit scalaire: $x \ rightarrow x + \ Delta x \ Rightarrow y \ rightarrow \ approx y + \ nabla_ {x} y \ cdot \ Delta x$ . Minimiser $y$ . Étant donné que le comportement de la fonction n'est connu que dans un petit voisinage à travers la dérivée, il est nécessaire de se déplacer par petites étapes, mais optimales, en minimisant le produit $\ nabla_ {x} y \ cdot \ Delta x$ . Par définition scolaire, le produit scalaire de deux vecteurs est le nombre égal au produit des longueurs de ces vecteurs par le cosinus de l'angle entre eux : $a \ cdot b = \ gauche | a \ droite | \ gauche | b \ droite | cos \ angle (a, b)$ . Pour une longueur fixe de vecteurs, ce produit atteint un minimum avec un cosinus de -1, c'est-à-dire à un angle de 180 degrés, lorsque les vecteurs sont dirigés dans des directions opposées. En conséquence, le produit scalaire minimum $\ nabla_ {x} y \ cdot \ Delta x$ atteint lorsque $\ Delta x$ dans le sens de l' anti-gradient .

Nous optimisons par la méthode Adam

Nous n'irons pas plus loin dans les méthodes de gradient, mais il existe de nombreuses variantes. Vous pouvez les lire dans l'article Méthodes d'optimisation des réseaux de neurones . Dans TensorFlow, de nombreux optimiseurs sont déjà implémentés. Par exemple, Adam:

 #       , #      adm = tf.train.AdamOptimizer(15).minimize(loss) #   ,    40000  session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, adm, feed_dict) print('PARAMETERS:', session.run(p))

 [Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 34205.72916492336 [...] ENDED ON STEP: 317, FINAL LOSS: 2.424142714263483e-12 PARAMETERS: [2.49999969 2.50000008]

Géré en 317 étapes. Beaucoup plus vite.

Nous optimisons par la méthode de Newton

Les actions des méthodes de second ordre peuvent être comparées à la conduite d'un snowboarder rationnel de freeride qui réfléchit longuement au prochain point de son itinéraire et prend en compte non seulement la pente à l'emplacement, mais aussi la courbure.

En fait, les méthodes de descente de gradient et les méthodes de second ordre tentent de deviner ( approximer ) la fonction au point courant. Les méthodes de gradient se concentrent uniquement sur la pente du graphique de la fonction au point - la dérivée première. Les méthodes du second ordre, en plus du biais, prennent en compte la courbure , la dérivée seconde: "si la courbure persiste, alors où sera le minimum?" Nous calculons et y allons:

Pour construire une telle approximation et calculer le point minimum estimé, vous pouvez utiliser la série Taylor . Pour le cas unidimensionnel, l'approximation par un polynôme de second ordre au point $a$ ressemble à ceci:

$f (x) \ approx f (a) + \ frac {f '(a) (x-a)} {1!} + \ frac {f' '(a) (x-a) ^ 2} {2!}$

Le minimum est atteint à $x = a - \ frac {f '(a)} {f' '(a)}$ . Le cas multidimensionnel semble plus sérieux:

Matrice de Hesse (vecteur entré - nombre à gauche)

La matrice de Hesse est une matrice carrée composée de dérivées secondes:

$\ boldsymbol {H} y_ {x} = \ begin {bmatrix} \ frac {\ partial ^ 2y} {\ partial x_1 ^ 2} & \ frac {\ partial ^ 2y} {\ partial x_1 \ partial x_2} & \ cdots & \ frac {\ partial ^ 2y} {\ partial x_1 \ partial x_N} \\ \ frac {\ partial ^ 2y} {\ partial x_2 \ partial x_1} & \ frac {\ partial ^ 2y} {\ partial x_2 ^ 2} & \ cdots & \ frac {\ partial ^ 2y} {\ partial x_2 \ partial x_N} \\ \ vdots & \ vdots & \ ddots & \ vdots \\ \ frac {\ partial ^ 2y} {\ partial x_N \ partiel x_1} & \ frac {\ partiel ^ 2y} {\ partiel x_N \ partiel x_2} & \ cdots & \ frac {\ partiel ^ 2y} {\ partiel x_N ^ 2} \ end {bmatrix}$

Approximation d'un polynôme de second ordre pour une fonction d'un vecteur à travers un gradient et une matrice de Hesse en un point $a$ ressemble à ceci:

$f (x) \ approx f (a) + (xa) ^ \ intercal [\ nabla_ {x} f (a)] + \ frac {1} {2!} (xa) ^ \ intercal [\ boldsymbol {H } f_ {x} (a)] (xa)$

Le minimum est atteint à $x = a - [\ boldsymbol {H} f_ {x} (a)] ^ {- 1} [\ nabla_ {x} f (a)]$ . La forme coïncide pratiquement avec le cas unidimensionnel: nous avons remplacé la première dérivée par un gradient, la seconde par une matrice de Hesse et fait une correction pour travailler avec des vecteurs. Il est impossible de diviser un vecteur par une matrice, par conséquent, la multiplication par la matrice inverse est utilisée. T signifie transposer . La formule implique que par défaut un vecteur est une colonne. Transposer transforme un vecteur de colonne en vecteur de ligne . Lors de l'implémentation sur TensorFlow, cela doit être pris en compte, mais en sens inverse: par défaut, le vecteur est une chaîne (tenseur unidimensionnel). Juste au cas où: la transposition n'est pas une rotation de 90 degrés, c'est la transformation de lignes en colonnes dans le même ordre.

Ainsi, l'étape de la méthode Newton a la forme suivante:

$\ boldsymbol {p} \ rightarrow \ boldsymbol {p} - [\ boldsymbol {H} loss_ {p} (\ boldsymbol {p})] ^ {- 1} [\ nabla_ {p} loss (\ boldsymbol {p} )]$

TensorFlow a tout pour implémenter cette méthode:

 #        hess = tf.hessians(loss, p)[0] #    - grad_col = tf.expand_dims(grad, -1) # ,      dp = tf.matmul(tf.linalg.inv(hess), grad_col) #  -  - dp = tf.squeeze(dp) #  p  dp    newton = opt.apply_gradients([(dp, p)]) #   ,    40000  session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, newton, feed_dict) print('PARAMETERS:', session.run(p))

 [Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 105.04357496954218 step: 4, current loss: 9.96663526704236 ENDED ON STEP: 6, FINAL LOSS: 5.882202372519996e-20 PARAMETERS: [2.5 2.5]

Assez 6 étapes:

Optimisé par l'algorithme de Gauss-Newton

La méthode de Newton a un inconvénient - la matrice de Hesse. Grâce à TensorFlow, nous pouvons le compter dans une seule ligne de code. Selon le wiki, Johann Karl Friedrich Gauss a fait la première mention de sa méthode en 1809. Le calcul de la matrice de Hesse pour plusieurs paramètres pour la méthode des moindres carrés pourrait alors prendre beaucoup de temps. Nous pouvons maintenant supposer que l'algorithme de Gauss-Newton utilise l'approximation de la matrice de Hesse à travers la matrice de Jacobi pour simplifier les calculs. Mais du point de vue de l'histoire, ce n'est pas le cas: Ludwig Otto Hesse (qui a développé la matrice qui porte son nom) est né en 1811 - 2 ans après la première mention de l'algorithme. Et Carl Gustav Jacobi avait 5 ans.

L'algorithme de Gauss-Newton ne fonctionne pas avec la fonction de perte. Il fonctionne avec la fonction résiduelle $r (p)$ . Cette fonction prend un vecteur d'entrée de paramètres $p$ et renvoie un vecteur résiduel . Dans notre cas, le vecteur $p$ se compose de 2 composants (paramètres $a$ et $b$ Fonctions de Rosenbrock) et le vecteur résiduel de $m$ (selon le nombre d'expériences). La fonction vectorielle de l'argument vecteur est obtenue. Sa dérivée:

Matrice de Jacobi (vecteur entré - vecteur libéré)

Considérons une fonction qui prend un vecteur en entrée et produit également un vecteur: $f: \ mathbb {R} ^ {N} \ rightarrow \ mathbb {R} ^ {M}$ . Dérivé $f$ au point $x$ a maintenant la taille $N \ fois M$ , appelée matrice de Jacobi , et se compose de toutes les combinaisons de dérivées partielles:

$\ boldsymbol {J} y_ {x} = \ begin {pmatrix} \ frac {\ partial y_ {1}} {\ partial x_ {1}} & \ cdots & \ frac {\ partial y_ {1}} {\ partiel x_ {N}} \\ \ vdots & \ ddots & \ vdots \\ \ frac {\ partial y_ {M}} {\ partial x_ {1}} & \ cdots & \ frac {\ partial y_ {M}} {\ partial x_ {N}} \ end {pmatrix}$

Vous remarquerez peut-être que les lignes de la matrice de Jacobi sont les gradients des composants $y$ . Objet $(i, j)$ matrices $\ frac {\ partial y} {\ partial x}$ est égal à $\ frac {\ partial y_ {i}} {\ partial x_ {j}}$ et nous dit combien va changer $y_ {i}$ lors du changement $x_ {j}$ sur une petite valeur. Comme dans les cas précédents, vous pouvez écrire:

$x \ rightarrow x + \ Delta x \ Rightarrow y \ rightarrow \ approx y + \ boldsymbol {J} y_ {x} \ Delta x$

Ici $\ boldsymbol {J} y_ {x}$ matrice $N \ fois M$ et $\ Delta x$ vecteur de taille $N$ ainsi le produit $\ boldsymbol {J} y_ {x} \ Delta x$ Est le produit de la matrice par le vecteur, résultant en un vecteur de taille $M$ .

Afin de ne pas se confondre dans l'abondance des personnages, nous supposons que $\ boldsymbol {J} _ {r}$ - Matrice de Jacobi des fonctions résiduelles au point courant $\ boldsymbol {p}$ . L'algorithme de Gauss-Newton peut alors s'écrire comme suit:

$\ boldsymbol {p} \ rightarrow \ boldsymbol {p} - [\ boldsymbol {J} _ {r} ^ \ intercal \ boldsymbol {J} _ {r}] ^ {- 1} \ boldsymbol {J} _ {r } ^ \ intercal r (\ boldsymbol {p})$

L'enregistrement sous la forme coïncide complètement avec l'enregistrement de la méthode de Newton. Seulement au lieu de la matrice de Hesse est utilisée $\ boldsymbol {J} _ {r} ^ \ intercal \ boldsymbol {J} _ {r}$ au lieu du gradient $\ boldsymbol {J} _ {r} ^ \ intercal r (\ boldsymbol {p})$ . Ensuite, nous verrons pourquoi une telle approximation peut être utilisée. En attendant, passons à l'implémentation sur TensorFlow:

 #  ,  TensorFlow     , #   ,        #  .  ,   : # 1)       tf.unstack(r) # 2)      tf.gradients(r_i, p) # 3)       tf.stack #      ,     #       j = tf.stack([tf.gradients(r_i, p)[0] for r_i in tf.unstack(r)]) jT = tf.transpose(j) #     - r_col = tf.expand_dims(r, -1) #      hess_approx = tf.matmul(jT, j) grad_approx = tf.matmul(jT, r_col) # ,      dp = tf.matmul(tf.linalg.inv(hess_approx), grad_approx) #  -  - dp = tf.squeeze(dp) #  p  dp    ng = opt.apply_gradients([(dp, p)]) #   ,    40000  session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, ng, feed_dict)

 [Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 14.653025157673625 step: 4, current loss: 4.3918079172783016e-07 ENDED ON STEP: 4, FINAL LOSS: 3.374364957618591e-17 PARAMETERS: [2.5 2.5]

Assez 4 étapes. Moins que pour la méthode de Newton.

Comme le montre le code, la fonction de perte n'est pas utilisée dans l'optimisation, uniquement pour les critères d'arrêt et de journalisation. Comment l'algorithme d'optimisation sait-il quelle fonction minimiser? La réponse est surprenante: pas question! Gauss-Newton minimise uniquement l' erreur quadratique moyenne .

Correction de la partie mathématique de l'article

Nous avons répété tous les calculs dont nous avions besoin. Corrigeons-le un peu afin de nous concentrer davantage uniquement sur la programmation et TensorFlow. Vous aurez peut-être besoin d'un crayon pour tracer la séquence d'actions mathématiques.

Il y a un modèle $y = f (x, p)$ où $x$ - vecteur $p$ - vecteur de paramètres de dimension $n$ et $y$ - scalaire. Des expériences reçues $m$ des points $(x_ {1}, y_ {1}), ..., (x_ {m}, y_ {m})$ ( paires de données ). La fonction résiduelle du vecteur dépend uniquement du vecteur de paramètre: $r (p) = (r_ {1} (p), ... r_ {m} (p))$ où $r_ {k} (p) = y_ {k} - \ widehat {y_ {k}} = y_ {k} - f (x_ {k}, p)$ . , $p$ , $x_{k}, y_{k}$ ? , $x_{k}, y_{k}$ , .

$p$ , ( sum of squared error — sse residual sum-of-squares — rss ) . mse sse , $m$ . . :

$loss(p) = r_{1}^2(p) + \cdots + r_{m}^2(p) = \sum_{k=1}^{m} r_{k}^2(p)$

$p$ $(p)$ .

, . — . — , $r^2$ $2r \frac{\partial r}{\partial p}$ . :

$\nabla_{p}loss = (\sum_{k=1}^{m}2r_{k}\frac{\partial r_{k}}{\partial p_{1}}, \cdots, \sum_{k=1}^{m}2r_{k}\frac{\partial r_{k}}{\partial p_{n}})$

. :

$[\boldsymbol{H}loss_{p}]_{ij} = \frac{\partial^2 loss}{\partial p_{i} \partial p_{j}} = \sum_{k=1}^{m}(2\frac{\partial r_{k}}{\partial p_{i}}\frac{\partial r_{k}}{\partial p_{j}} + 2r_{k}\frac{\partial^2 r_{k}}{\partial p_{i}\partial p_{j}})$

. , , ${(uv)}'={u}'v+u{v}'$ .
Super! .

, , , — $2r_{k}\frac{\partial^2 r_{k}}{\partial p_{i}\partial p_{j}}$ . , , $r_{k}$ , . — . , ? -.

$\boldsymbol{J}_{r} = \begin{pmatrix} \frac{\partial r_{1}}{\partial p_{1}} & \cdots & \frac{\partial r_{1}}{\partial p_{n}}\\ \vdots & \ddots & \vdots \\ \frac{\partial r_{m}}{\partial p_{1}} & \cdots & \frac{\partial p_{m}}{\partial p_{n}} \end{pmatrix}$

, , . Notez que:

$2\boldsymbol{J}_{r}^\intercal\boldsymbol{J}_{r} \approx \boldsymbol{H}loss_{p}$

"" . ( ). , — $2r_{k}\frac{\partial^2 r_{k}}{\partial p_{i}\partial p_{j}}$ , .
( ):

$2\boldsymbol{J}_{r}^\intercal r = \nabla_{p}loss$

, , - — , mse .

. , , . $m$ $(x_{1}, y_{1}), ..., (x_{m}, y_{m})$ , $y = rosenbrock(x, p)$ . $p$ , .

, : " . - ! ". , , , ( supervised learning ). , . : ( training set ) — ; — ( prediction model ) ; — , .

( multi-layer perceptron neural network mlp ). , , :

( starting values ) . Xavier'a, .
( overfitting ). — . , . — .
( scaling of the input ). , .

9 . 500:

 #    def get_random_rosenbrock_data_points(m): result = np.zeros((m, 3)) result[:, 0] = np.random.uniform(-2, 2, m) result[:, 1] = np.random.uniform(-2, 2, m) result[:, 2] = rosenbrock(result[:, 0], result[:, 1], 2.5, 2.5) return result m = 500 data_points = get_random_rosenbrock_data_points(m) # overfitting   ,      validation_data_points = get_random_rosenbrock_data_points(m)

500 . — ( learner ), ( outcome measurement ) ( features ) .

( network diagram ). MatLab:

( input ). $W$ ( weights ) 2x10, $b$ ( bias ) 10, ( activation ). () ( hidden layer ) 10 . , , ( output ).

, , ( $tanh$ ):

$\begin{matrix} h_{1} = tanh(xW_{1} + b_{1})\\ \widehat{y} = h_{1}W_{2} + b_{2} \end{matrix}$

$h_1 = tanh(\begin{bmatrix} x_1 & x_2 \end{bmatrix}\begin{bmatrix} w^{(1)}_{1,1} & \cdots& w^{(1)}_{1,10} \\ w^{(1)}_{2,1} &\cdots& w^{(1)}_{2,10} \end{bmatrix} + \begin{bmatrix} b^{(1)}_1 & \cdots & b^{(1)}_{10} \end{bmatrix}) \\ \widehat{y} = \begin{bmatrix}h^{(1)}_1 & \cdots & h^{(1)}_{10}\end{bmatrix} \begin{bmatrix} w^{(2)}_{1,1} \\ \vdots \\ w^{(2)}_{1,10} \\ \end{bmatrix} + b_2$

. $W_{1}$ "" $h_{1}$ , - $W_{2}$ . 41 . , .

$m \times 2$ , . - $\widehat{y}$ de $m$ :

 #     10 "" n_hidden = 10 #      Xavier'a initializer = tf.contrib.layers.xavier_initializer() #    x = tf.placeholder(tf.float64, shape=[m, 2]) y = tf.placeholder(tf.float64, shape=[m, 1]) #         W1 = tf.Variable(initializer([2, n_hidden], dtype=tf.float64)) b1 = tf.Variable(initializer([1, n_hidden], dtype=tf.float64)) #   ,  tanh   h1 = tf.nn.tanh(tf.matmul(x, W1) + b1) #        W2 = tf.Variable(initializer([n_hidden, 1], dtype=tf.float64)) b2 = tf.Variable(initializer([1], dtype=tf.float64)) #   y_hat = tf.matmul(h1, W2) + b2 #  r = y - y_hat #   mse     loss = tf.reduce_mean(tf.square(r)) #      placeholder feed_dict = {x: data_points[:,0:2], y: data_points[:,2:3]} validation_feed_dict = {x: validation_data_points[:,0:2], y: validation_data_points[:,2:3]}

Adam

Adam $rosenbrock$ . mse :

 #    adm = tf.train.AdamOptimizer(1e-2).minimize(loss) session.run(tf.global_variables_initializer()) #   ,    40000  train(1e-10, 40000, loss, adm, feed_dict) print('VALIDATION LOSS: '+str(session.run(loss, validation_feed_dict)))

 [Out]: step: 1, current loss: 671.4242576535694 [...] ENDED ON STEP: 40000, FINAL LOSS: 0.22862158574440725 VALIDATION LOSS: 0.29000289644978866

. : , , .

$rosenbrock$ 2 . :

. 9 , 500. .
. - $p$ , .

 #      y   x def jacobian(y, x): loop_vars = [ tf.constant(0, tf.int32), tf.TensorArray(tf.float64, size=m), ] #  -   #      _, jacobian = tf.while_loop( lambda i, _: i < m, #           #   (-),   x     lambda i, res: (i+1, res.write(i, tf.reshape(tf.gradients(y[i], x), (-1,)))), loop_vars) #       return jacobian.stack() #       r_flat = tf.squeeze(r) #        #       parms = [W1, b1, W2, b2] parms_sizes = [tf.size(p) for p in parms] j = tf.concat([jacobian(r_flat, p) for p in parms], 1) jT = tf.transpose(j) #           hess_approx = tf.matmul(jT, j) grad_approx = tf.matmul(jT, r)

$\boldsymbol{J}r_{p}$ . , 4 $W_1, b_1, W_2, b_2$ . 4 $\boldsymbol{J}r_{W_1}, \boldsymbol{J}r_{b_1}, \boldsymbol{J}r_{W_2}, \boldsymbol{J}r_{b_2}$ tf.concat .

. tf.while_loop , $r_i$ , , stack .

$r_i$ $W_1$ : $\begin{bmatrix} \frac{\partial r_i}{\partial w^{(1)}_{1,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{1,10}} \\ \frac{\partial r_i}{\partial w^{(1)}_{2,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{2,10}} \end{bmatrix}$ . tf.reshape (-1,) $\begin{bmatrix} \frac{\partial r_i}{\partial w^{(1)}_{1,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{1,10}} & \frac{\partial r_i}{\partial w^{(1)}_{2,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{2,10}} \end{bmatrix}$ .

. - . — TensorFlow . — - - $W_1, b_1, W_2, b_2$ . -. Levenberg-Marquardt Jupyter Notebook rosenbrock_train.py . , TensorFlow . - , ( ) , , .

-

hess_approx grad_approx -. $rosenbrock$ , . :

: $\Delta \boldsymbol{p} = \begin{bmatrix}\Delta w^{(1)}_{1,1} & \cdots & \Delta w^{(1)}_{2,10} & \Delta b^{(1)}_1 & \cdots & \Delta b^{(1)}_{10} & \Delta w^{(2)}_{1,1} & \cdots & \Delta w^{(2)}_{1,10} & \Delta b_2\end{bmatrix}$
:
$\Delta W_{1} = \begin{bmatrix}\Delta w^{(1)}_{1,1} & \cdots & \Delta w^{(1)}_{2,10} \end{bmatrix}$ , $\Delta b_{1} = \begin{bmatrix} \Delta b^{(1)}_1 & \cdots & \Delta b^{(1)}_{10} \end{bmatrix}$ , $\Delta W_{2} = \begin{bmatrix} \Delta w^{(2)}_{1,1} & \cdots & \Delta w^{(2)}_{1,10} \end{bmatrix}$ , $\Delta b_{2} = \begin{bmatrix} \Delta b_2\end{bmatrix}$ .
, :
$\Delta W_{1} = \begin{bmatrix} \Delta w^{(1)}_{1,1} & \cdots & \Delta w^{(1)}_{1,10} \\ \Delta w^{(1)}_{2,1} &\cdots & \Delta w^{(1)}_{2,10} \end{bmatrix}$ , $\Delta W_{2} = \begin{bmatrix} \Delta w^{(2)}_{1,1} \\ \vdots \\ \Delta w^{(2)}_{1,10} \\ \end{bmatrix}$
.

 # 1.     dp_flat = tf.matmul(tf.linalg.inv(hess_approx), grad_approx) # 2.     dps = tf.split(dp_flat, parms_sizes, 0) # 3.     for i in range(len(dps)): dps[i] = tf.reshape(dps[i], parms[i].shape) # 4.  :       gn = opt.apply_gradients(zip(dps, parms)) #   session.run(tf.global_variables_initializer()) train(1e-10, 100, loss, gn, feed_dict)

 [Out]: step: 1, current loss: 548.8468777701685 step: 2, current loss: 49648941.340197295 InvalidArgumentError: Input is not invertible.

- . , . - , .

, .

-

. Matlab trainlm . . MathWorks.

- : $\boldsymbol{p} \rightarrow \boldsymbol{p}-[\boldsymbol{J}_{r}^\intercal\boldsymbol{J}_{r}]^{-1}\boldsymbol{J}_{r}^\intercal r(\boldsymbol{p})$ . - :

$\boldsymbol{p} \rightarrow \boldsymbol{p}-[\boldsymbol{J}_{r}^\intercal\boldsymbol{J}_{r}+\mu \boldsymbol{I}]^{-1}\boldsymbol{J}_{r}^\intercal r(\boldsymbol{p})$

$\ mu$ $I$ $n$ ( ). $\ mu$ , -. , . , LM -.

 mu = tf.placeholder(tf.float64, shape=[1]) n = tf.add_n(parms_sizes) I = tf.eye(n, dtype=tf.float64) # 1.     dp_flat = tf.matmul(tf.linalg.inv(hess_approx + tf.multiply(mu, I)), grad_approx) # 2.     dps = tf.split(dp_flat, parms_sizes, 0) # 3.     for i in range(len(dps)): dps[i] = tf.reshape(dps[i], parms[i].shape) # 4.  :       lm = opt.apply_gradients(zip(dps, parms))

$\ mu$ ? LM - . , . , $\ mu$ , . — , mse . , :

 #       store = [tf.Variable(tf.zeros(p.shape, dtype=tf.float64)) for p in parms] #  TensorFlow       save_parms = [tf.assign(s, p) for s, p in zip(store, parms)] restore_parms = [tf.assign(p, s) for s, p in zip(store, parms)] #   mu    3. feed_dict[mu] = np.array([3.]) step = 0 session.run(tf.global_variables_initializer()) #    mse current_loss = session.run(loss, feed_dict) #    100   while current_loss > 1e-10 and step < 100: step += 1 #  1, 2, 4...   if math.log(step, 2).is_integer(): print(f'step: {step}, mu: {feed_dict[mu][0]} current loss: {current_loss}') #    session.run(save_parms) # ,     mse while True: #    session.run(lm, feed_dict) new_loss = session.run(loss, feed_dict) if new_loss > current_loss: #  -  mu  10     feed_dict[mu] *= 10 session.run(restore_parms) else: #  -  mu  10     feed_dict[mu] /= 10 current_loss = new_loss break print(f'ENDED ON STEP: {step}, FINAL LOSS: {current_loss}') print('VALIDATION LOSS: '+str(session.run(loss, validation_feed_dict)))

 [Out]: step: 1, mu: 3.0 current loss: 692.6211687622557 [...] ENDED ON STEP: 100, FINAL LOSS: 0.012346989371823602 VALIDATION LOSS: 0.01859463694102034

100 LM mse 10 , 40 .

. , . , rosenbrock_train.py .

2D . . . , " " ( curse of dimentionality , Bellman, 1961). . .

$f(\boldsymbol{x}) = \sum_{i=1}^{N-1}\left [ 100(x_{i+1} - x_{i}^2)^2 + (1-x_{i})^2 \right ], \boldsymbol{x}=[x_1 \cdots x_{N}]\in \mathbb{R}^N$

rosenbrock_train.py get_rand_rosenbrock_points .

-

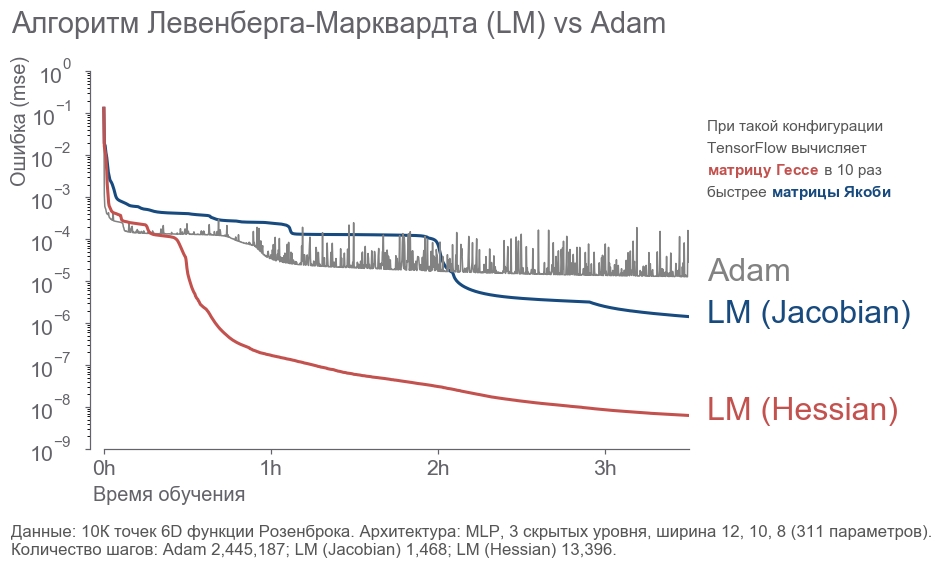
- : " ! 4 , 300! ". , ( ) -. , , . - . . : ? , . . , - :

10 000 6D .
3 12, 10, 8 (311 ).
.
3.5 .

. - 2 . LM . 20 .

rosenbrock_train.py . . , .

Conclusion

, . " ", , . , . , 273 . - , .

, :

.
( ) -:
[1] Petros Drineas, Ravi Kannan, and Michael W. Mahoney. 2006. Fast Monte Carlo Algorithms for Matrices I: Approximating Matrix Multiplication. SIAM J. Comput. 36, 1 (July 2006), 132-157. DOI= http://dx.doi.org/10.1137/S0097539704442684
[2] Adelman, M., & Silberstein, M. (2018). Faster Neural Network Training with Approximate Tensor Operations. CoRR, abs/1805.08079.

, - . , . "".

Implémentation de l'algorithme de Levenberg-Marquardt pour l'optimisation des réseaux de neurones sur TensorFlow