Nous approchons la fonction en utilisant un réseau de neurones

Afin de maîtriser les bibliothèques pour travailler avec les réseaux de neurones, nous allons résoudre le problème d'approximation de la fonction d'un argument en utilisant des algorithmes de réseau de neurones pour la formation et la prédiction.

Entrée

Soit une fonction f donnée: [x0, x1] -> R

Nous approchons la fonction donnée f par la formule

P(x) = SUM W[i]*E(x,M[i]) 

où

• i = 1..n
• M [i] de R
• W [i] de R
• E (x, M) = {0, pour x <M; 1/2, avec x = M; 1, pour x> M

Évidemment, avec une distribution uniforme des valeurs de M [i] sur l'intervalle (x0, x1), il existe de telles quantités W [i] pour lesquelles la formule P (x) correspondra le mieux à la fonction f (x). De plus, pour des valeurs données de M [i] définies sur l'intervalle (x0, x1) et ordonnées par ordre croissant, nous pouvons décrire un algorithme séquentiel pour calculer les quantités W [i] pour la formule P (x).

Et voici le réseau neuronal

Nous transformons la formule P (x) = SUM W [i] * E (x, M [i]) en un modèle de réseau neuronal avec un neurone d'entrée, un neurone de sortie et n neurones de couche cachée

 P(x) = SUM W[i]*S(K[i]*x + B[i]) + C 

où

• variable x - couche «d'entrée» constituée d'un neurone
• {K, B} - paramètres de la couche "cachée", composée de n neurones et fonction d'activation - sigmoïde
• {W, C} - paramètres de la couche "de sortie", constituée d'un neurone, qui calcule la somme pondérée de ses entrées.
• S est un sigmoïde,

tout

• paramètres initiaux de la couche "cachée" K [i] = 1
• les paramètres initiaux de la couche "cachée" B [i] sont répartis uniformément sur le segment (-x1, -x0)

Tous les paramètres du réseau neuronal K, B, W et C sont déterminés en entraînant le réseau neuronal sur des échantillons (x, y) des valeurs de la fonction f.

Sigmoïde

Sigmoïde est une fonction non linéaire croissante monotone lisse

• S (x) = 1 / (1 + exp (-x)).

Le programme

Nous utilisons le package Tensorflow pour décrire notre réseau neuronal.

 #        x = tf.placeholder(tf.float32, [None, 1], name="x") #        y = tf.placeholder(tf.float32, [None, 1], name="y") #   nn = tf.layers.dense(x, hiddenSize, activation=tf.nn.sigmoid, kernel_initializer=tf.initializers.ones(), bias_initializer=tf.initializers.random_uniform(minval=-x1, maxval=-x0), name="hidden") #   model = tf.layers.dense(nn, 1, activation=None, name="output") #    cost = tf.losses.mean_squared_error(y, model) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) 

La formation

 init = tf.initializers.global_variables() with tf.Session() as session: session.run(init) for _ in range(iterations): train_dataset, train_values = generate_test_values() session.run(train, feed_dict={ x: train_dataset, y: train_values }) 

Texte intégral

 import math import numpy as np import tensorflow as tf import matplotlib.pyplot as plt x0, x1 = 10, 20 #    test_data_size = 2000 #      iterations = 20000 #    learn_rate = 0.01 #   hiddenSize = 10 #    #     def generate_test_values(): train_x = [] train_y = [] for _ in range(test_data_size): x = x0+(x1-x0)*np.random.rand() y = math.sin(x) #   train_x.append([x]) train_y.append([y]) return np.array(train_x), np.array(train_y) #        x = tf.placeholder(tf.float32, [None, 1], name="x") #        y = tf.placeholder(tf.float32, [None, 1], name="y") #   nn = tf.layers.dense(x, hiddenSize, activation=tf.nn.sigmoid, kernel_initializer=tf.initializers.ones(), bias_initializer=tf.initializers.random_uniform(minval=-x1, maxval=-x0), name="hidden") #   model = tf.layers.dense(nn, 1, activation=None, name="output") #    cost = tf.losses.mean_squared_error(y, model) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) init = tf.initializers.global_variables() with tf.Session() as session: session.run(init) for _ in range(iterations): train_dataset, train_values = generate_test_values() session.run(train, feed_dict={ x: train_dataset, y: train_values }) if(_ % 1000 == 999): print("cost = {}".format(session.run(cost, feed_dict={ x: train_dataset, y: train_values }))) train_dataset, train_values = generate_test_values() train_values1 = session.run(model, feed_dict={ x: train_dataset, }) plt.plot(train_dataset, train_values, "bo", train_dataset, train_values1, "ro") plt.show() with tf.variable_scope("hidden", reuse=True): w = tf.get_variable("kernel") b = tf.get_variable("bias") print("hidden:") print("kernel=", w.eval()) print("bias = ", b.eval()) with tf.variable_scope("output", reuse=True): w = tf.get_variable("kernel") b = tf.get_variable("bias") print("output:") print("kernel=", w.eval()) print("bias = ", b.eval()) 

Voilà ce qui s'est passé

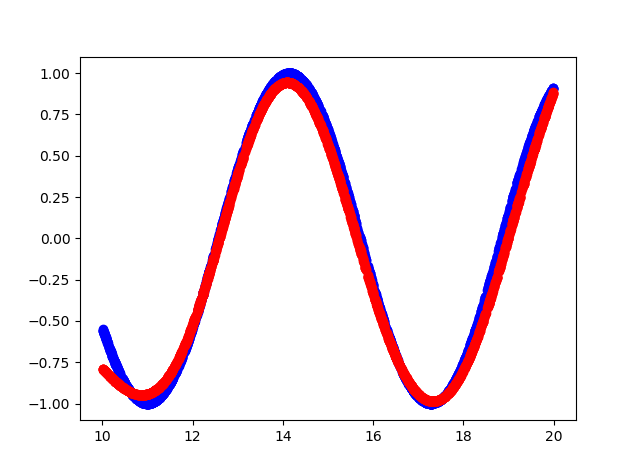
• Le bleu est la fonction d'origine.
• Couleur rouge - approximation de la fonction

Sortie console

 cost = 0.15786637365818024 cost = 0.10963975638151169 cost = 0.08536215126514435 cost = 0.06145831197500229 cost = 0.04406769573688507 cost = 0.03488277271389961 cost = 0.026663536205887794 cost = 0.021445846185088158 cost = 0.016708852723240852 cost = 0.012960446067154408 cost = 0.010525770485401154 cost = 0.008495906367897987 cost = 0.0067353141494095325 cost = 0.0057082874700427055 cost = 0.004624188877642155 cost = 0.004093789495527744 cost = 0.0038146725855767727 cost = 0.018593043088912964 cost = 0.010414039716124535 cost = 0.004842184949666262 hidden: kernel= [[1.1523403 1.181032 1.1671464 0.9644377 0.8377886 1.0919508 0.87283015 1.0875995 0.9677301 0.6194152 ]] bias = [-14.812331 -12.219926 -12.067375 -14.872566 -10.633507 -14.014006 -13.379829 -20.508204 -14.923473 -19.354435] output: kernel= [[ 2.0069902 ] [-1.0321712 ] [-0.8878887 ] [-2.0531905 ] [ 1.4293027 ] [ 2.1250408 ] [-1.578137 ] [ 4.141281 ] [-2.1264815 ] [-0.60681605]] bias = [-0.2812019] 

Code source

https://github.com/dprotopopov/nnfunc