Je vous présente la traduction d'un chapitre du livre Hands-On Data Science with Anaconda
«Analyse prédictive des données - modélisation et validation»
Notre objectif principal dans la réalisation de diverses analyses de données est de rechercher des modèles pour prédire ce qui pourrait se produire à l'avenir. Pour le marché boursier, les chercheurs et les experts effectuent divers tests pour comprendre les mécanismes du marché. Dans ce cas, vous pouvez poser beaucoup de questions. Quel sera le niveau de l'indice de marché au cours des cinq prochaines années? Quelle sera la prochaine fourchette de prix pour IBM? La volatilité du marché augmentera-t-elle ou diminuera-t-elle à l'avenir? Quel pourrait être l'effet si les gouvernements modifient leurs politiques fiscales? Quels sont les gains et les pertes potentiels si un pays déclenche une guerre commerciale avec un autre? Comment prédisons-nous le comportement des consommateurs en analysant certaines variables connexes? Peut-on prédire la probabilité qu'un étudiant diplômé réussisse? Pouvons-nous trouver un lien entre le comportement spécifique d'une maladie particulière?
Par conséquent, nous examinerons les sujets suivants:
- Comprendre l'analyse prédictive des données
- Ensembles de données utiles
- Prévision des événements futurs
- Sélection du modèle
- Test de causalité de Granger
Comprendre l'analyse prédictive des données
Les gens peuvent avoir de nombreuses questions concernant les événements futurs.
- Un investisseur, s'il peut prédire le mouvement futur des cours boursiers, il peut faire un gros profit.
- Les entreprises, si elles pouvaient prédire la tendance de leurs produits, pourraient augmenter le prix de leurs actions et leur part de marché.
- Les gouvernements, s'ils pouvaient prédire l'impact du vieillissement de la population sur la société et l'économie, seraient davantage incités à élaborer de meilleures politiques en termes de budget de l'État et d'autres décisions stratégiques pertinentes.
- Les universités, si elles pouvaient bien comprendre la demande du marché en termes de qualité et de compétences pour leurs diplômés, elles pourraient développer un ensemble de meilleurs programmes ou lancer de nouveaux programmes pour répondre aux besoins futurs de la main-d'œuvre.
Pour un meilleur pronostic, les chercheurs devraient considérer de nombreuses questions. Par exemple, les données d'exemple sont-elles trop petites? Comment supprimer les variables manquantes? Cet ensemble de données est-il biaisé en termes de procédures de collecte de données? Que pensons-nous des extrêmes ou des émissions? Qu'est-ce que la saisonnalité et comment la gérer? Quels modèles devons-nous utiliser? Ce chapitre abordera certains de ces problèmes. Commençons par un ensemble de données utile.
Ensembles de données utiles
L'une des meilleures sources de données est le
référentiel d'apprentissage automatique UCI . Après avoir visité le site, nous verrons la liste suivante:

Par exemple, si vous sélectionnez le premier jeu de données (Abalone), nous verrons ce qui suit. Pour économiser de l'espace, seul le haut est affiché:

De là, les utilisateurs peuvent télécharger l'ensemble de données et trouver des définitions de variables. Le code suivant peut être utilisé pour charger un ensemble de données:
dataSet<-"UCIdatasets" path<-"http://canisius.edu/~yany/RData/" con<-paste(path,dataSet,".RData",sep='') load(url(con)) dim(.UCIdatasets) head(.UCIdatasets)
La sortie correspondante est affichée ici:

De la conclusion précédente, nous savons que dans l'ensemble de données il y a 427 observations (ensembles de données). Pour chacun d'eux, nous avons 7 fonctions liées, telles que
Nom, Data_Types, Default_Task, Attribute_Types, N_Instances (nombre d'instances),
N_Attributes (nombre d'attributs) et
Year . Une variable appelée
Default_Task peut être interprétée comme l'utilisation principale de chaque ensemble de données. Par exemple, un premier ensemble de données appelé
Abalone peut être utilisé pour la
classification . La fonction
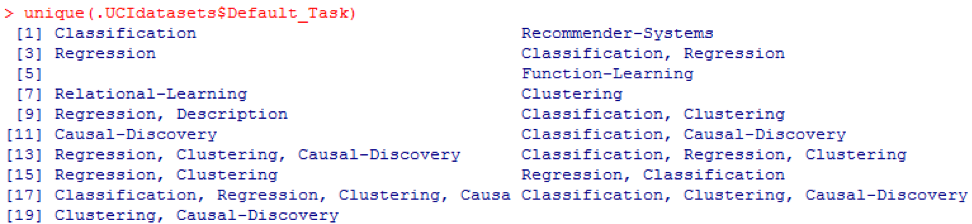
unique () peut être utilisée pour rechercher toutes les
Default_Task possibles affichées ici:
Package R AppliedPredictiveModeling
Ce package comprend de nombreux jeux de données utiles qui peuvent être utilisés pour ce chapitre et d'autres. La façon la plus simple de trouver ces ensembles de données est d'utiliser la fonction
help () illustrée ici:
library(AppliedPredictiveModeling) help(package=AppliedPredictiveModeling)
Ici, nous montrons quelques exemples de chargement de ces jeux de données. Pour charger un ensemble de données, nous utilisons la fonction
data () . Pour le premier ensemble de données appelé
abalone , nous avons le code suivant:
library(AppliedPredictiveModeling) data(abalone) dim(abalone) head(abalone)
La sortie est la suivante:

Parfois, un grand ensemble de données comprend plusieurs sous-ensembles de données:
library(AppliedPredictiveModeling) data(solubility) ls(pattern="sol")
[1] "solTestX" "solTestXtrans" "solTestY" [4] "solTrainX" "solTrainXtrans" "solTrainY"
Pour charger chaque ensemble de données, nous pourrions utiliser les fonctions
dim () ,
head () ,
tail () et
summary () .
Analyse des séries chronologiques
Les séries chronologiques peuvent être définies comme un ensemble de valeurs obtenues à des moments consécutifs, souvent avec des intervalles égaux entre eux. Il existe différentes périodes, telles que annuelle, trimestrielle, mensuelle, hebdomadaire et quotidienne. Pour les séries chronologiques du PIB (produit intérieur brut), nous utilisons généralement des données trimestrielles ou annuelles. Pour les devis - fréquences annuelles, mensuelles et quotidiennes. En utilisant le code suivant, nous pouvons obtenir des données sur le PIB américain à la fois trimestriellement et pour une période annuelle:
ath<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPannual" con<-paste(path,dataSet,".RData",sep='') load(url(con)) head(.usGDPannual)
YEAR GDP 1 1930 92.2 2 1931 77.4 3 1932 59.5 4 1933 57.2 5 1934 66.8 6 1935 74.3
dataSet<-"usGDPquarterly" con<-paste(path,dataSet,".RData",sep='') load(url(con)) head(.usGDPquarterly)
DATE GDP_CURRENT GDP2009DOLLAR 1 1947Q1 243.1 1934.5 2 1947Q2 246.3 1932.3 3 1947Q3 250.1 1930.3 4 1947Q4 260.3 1960.7 5 1948Q1 266.2 1989.5 6 1948Q2 272.9 2021.9
Cependant, nous avons de nombreuses questions pour l'analyse des séries chronologiques. Par exemple, du point de vue de la macroéconomie, nous avons des cycles économiques ou économiques. Les industries ou les entreprises peuvent avoir une saisonnalité. Par exemple, en utilisant l'industrie agricole, les agriculteurs dépenseront plus au printemps et à l'automne et moins en hiver. Pour les détaillants, ils auraient un énorme afflux d'argent à la fin de l'année.
Pour manipuler les séries chronologiques, nous pourrions utiliser les nombreuses fonctionnalités utiles incluses dans le package R, appelées
timeSeries . Dans l'exemple, nous prenons les données moyennes quotidiennes avec une fréquence hebdomadaire:
library(timeSeries) data(MSFT) x <- MSFT by <- timeSequence(from = start(x), to = end(x), by = "week") y<-aggregate(x,by,mean)
Nous pourrions également utiliser la fonction
head () pour voir quelques observations:
head(x)
GMT Open High Low Close Volume 2000-09-27 63.4375 63.5625 59.8125 60.6250 53077800 2000-09-28 60.8125 61.8750 60.6250 61.3125 26180200 2000-09-29 61.0000 61.3125 58.6250 60.3125 37026800 2000-10-02 60.5000 60.8125 58.2500 59.1250 29281200 2000-10-03 59.5625 59.8125 56.5000 56.5625 42687000 2000-10-04 56.3750 56.5625 54.5000 55.4375 68226700
head(y)
GMT Open High Low Close Volume 2000-09-27 63.4375 63.5625 59.8125 60.6250 53077800 2000-10-04 59.6500 60.0750 57.7000 58.5500 40680380 2000-10-11 54.9750 56.4500 54.1625 55.0875 36448900 2000-10-18 53.0375 54.2500 50.8375 52.1375 50631280 2000-10-25 61.7875 64.1875 60.0875 62.3875 86457340 2000-11-01 66.1375 68.7875 65.8500 67.9375 53496000
Prévision des événements futurs
Il existe de nombreuses méthodes que nous pourrions utiliser pour essayer de prédire l'avenir, telles que la moyenne mobile, la régression, l'autorégression, etc. Commençons par la plus simple pour la moyenne mobile:
movingAverageFunction<- function(data,n=10){ out= data for(i in n:length(data)){ out[i] = mean(data[(i-n+1):i]) } return(out) }
Dans le code précédent, la valeur par défaut pour le nombre de périodes est 10. Nous pourrions utiliser un ensemble de données appelé MSFT inclus dans le package R appelé
timeSeries (voir le code suivant):
library(timeSeries) data(MSFT) p<-MSFT$Close
[1] 60.6250 61.3125 60.3125 59.1250 56.5625 55.4375
head(ma)
[1] 60.62500 61.31250 60.75000 60.25000 58.66667 57.04167
mean(p[1:3])
[1] 60.75
mean(p[2:4])
[1] 60.25
En mode manuel, nous constatons que la moyenne des trois premières valeurs de
x correspond à la troisième valeur de
y . D'une certaine manière, nous pourrions utiliser une moyenne mobile pour prédire l'avenir.
Dans l'exemple suivant, nous montrerons comment évaluer les rendements attendus du marché l'année prochaine. Ici, nous utilisons l'indice S & P500 et la valeur annuelle moyenne historique comme valeurs attendues. Les premières commandes sont utilisées pour charger un jeu de données associé appelé
.sp500monthly . Le but du programme est d'évaluer la moyenne annuelle moyenne et l'intervalle de confiance à 90%:
library(data.table) path<-'http://canisius.edu/~yany/RData/' dataSet<-'sp500monthly.RData' link<-paste(path,dataSet,sep='') load(url(link))
[min mean max ]
cat(min2,ourMean,max2,"\n")
0.05032956 0.09022369 0.1301178
Comme vous pouvez le voir sur les résultats, le rendement annuel moyen historique du S & P500 est de 9%. Mais on ne peut pas dire que la rentabilité de l’indice l’année prochaine sera de 9%, car cela peut aller de 5% à 13%, et ce sont d'énormes fluctuations.
Saisonnalité
Dans l'exemple suivant, nous montrons l'utilisation de l'autocorrélation. Tout d'abord, nous téléchargeons un package R appelé
astsa , qui signifie analyse statistique des séries chronologiques. Ensuite, nous chargeons le PIB américain avec une fréquence trimestrielle:
library(astsa) path<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPquarterly" con<-paste(path,dataSet,".RData",sep='') load(url(con)) x<-.usGDPquarterly$DATE y<-.usGDPquarterly$GDP_CURRENT plot(x,y) diff4 = diff(y,4) acf2(diff4,24)
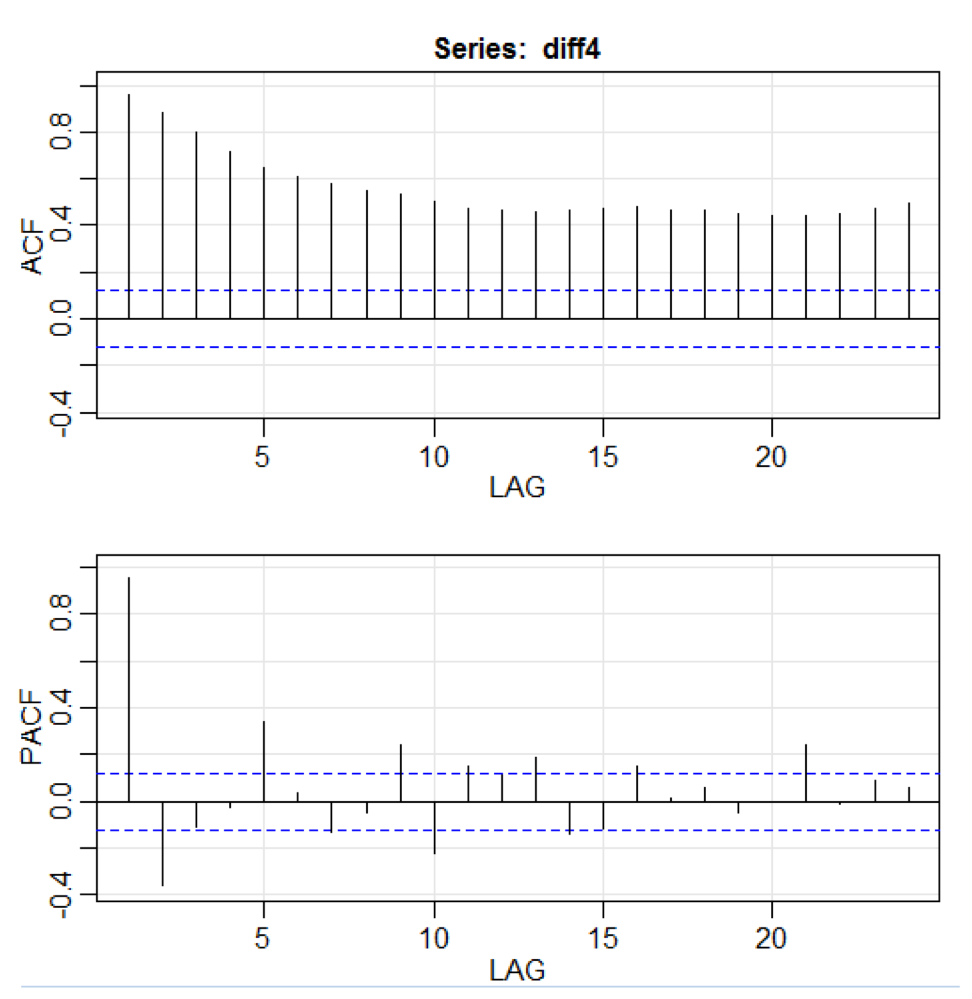
Dans le code ci-dessus, la fonction
diff () accepte la différence, par exemple, la valeur actuelle moins la valeur précédente. Une deuxième valeur d'entrée indique un retard. Une fonction appelée
acf2 () est utilisée pour créer et imprimer les séries chronologiques ACF et PACF. ACF signifie fonction d'autocovariance et PACF signifie fonction d'autocorrélation partielle. Les graphiques pertinents sont présentés ici:
Visualisation des composants
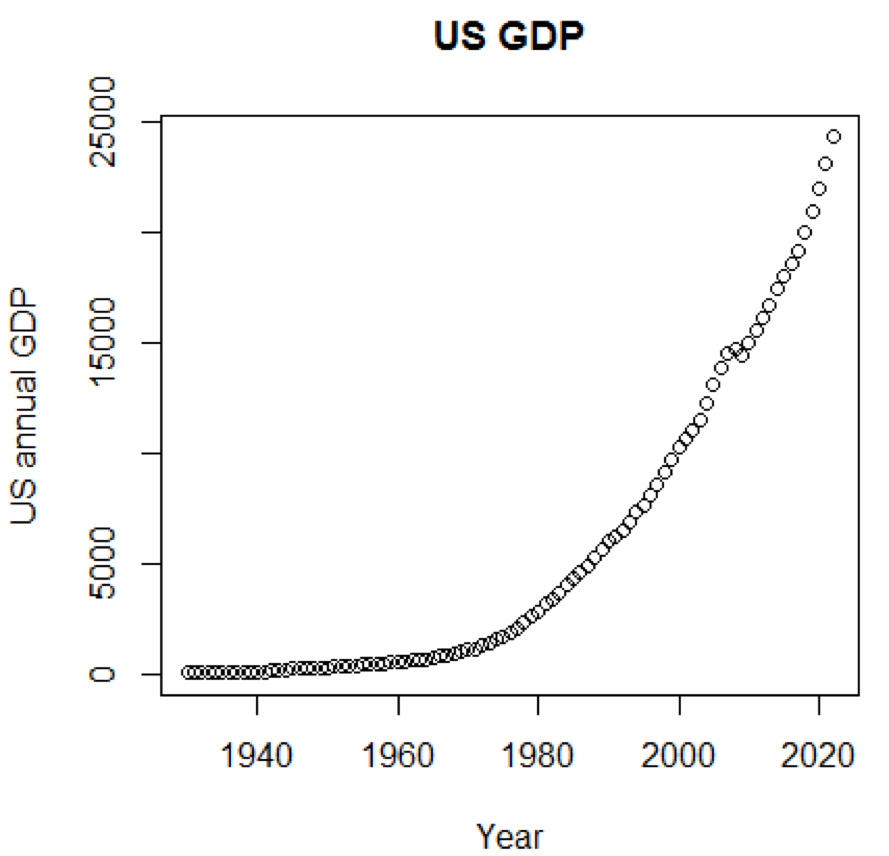
De toute évidence, les concepts et les ensembles de données seraient beaucoup plus compréhensibles si nous pouvions utiliser des graphiques. Le premier exemple montre les fluctuations du PIB américain au cours des cinq dernières décennies:
path<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPannual" con<-paste(path,dataSet,".RData",sep='') load(url(con)) title<-"US GDP" xTitle<-"Year" yTitle<-"US annual GDP" x<-.usGDPannual$YEAR y<-.usGDPannual$GDP plot(x,y,main=title,xlab=xTitle,ylab=yTitle)
L'horaire correspondant est affiché ici:
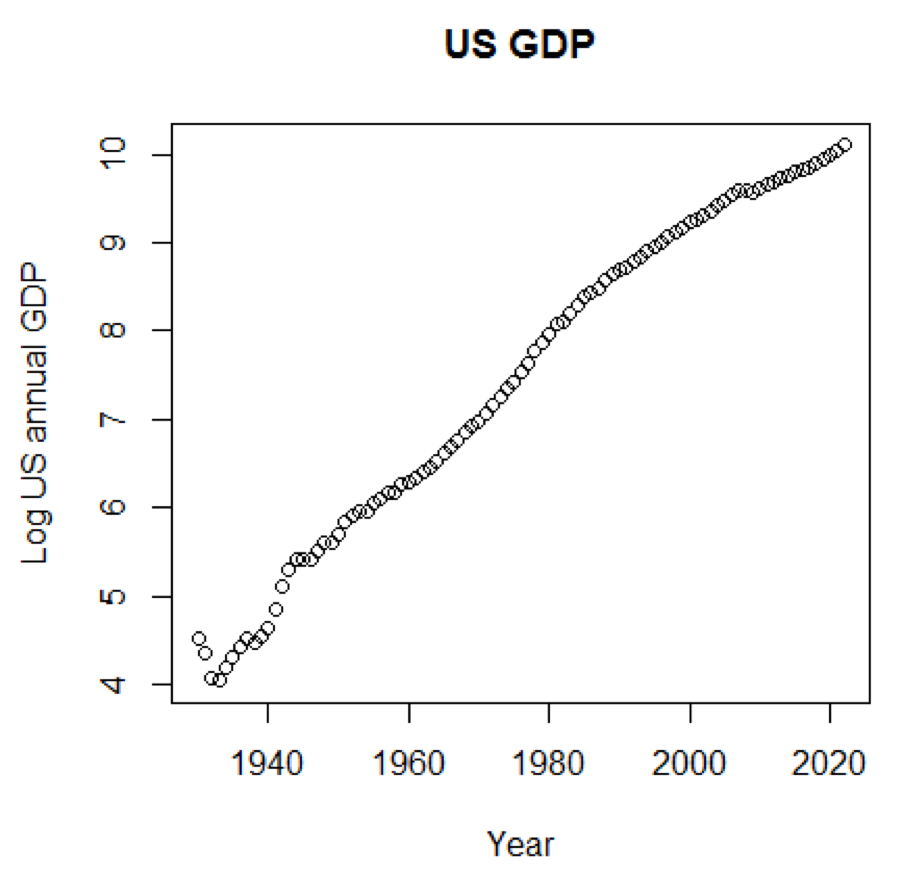
Si nous utilisions l'échelle logarithmique du PIB, nous aurions le code et le graphique suivants:
yTitle<-"Log US annual GDP" plot(x,log(y),main=title,xlab=xTitle,ylab=yTitle)
Le graphique suivant est proche d'une ligne droite:
Forfait R - LiblineaR
Ce package est un modèle prédictif linéaire basé sur la bibliothèque LIBLINEAR C / C ++. Voici un exemple d'utilisation du jeu de données
iris . Le programme essaie de prédire à quelle catégorie une plante appartient en utilisant les données de formation:
library(LiblineaR) data(iris) attach(iris) x=iris[,1:4] y=factor(iris[,5]) train=sample(1:dim(iris)[1],100) xTrain=x[train,];xTest=x[-train,] yTrain=y[train]; yTest=y[-train] s=scale(xTrain,center=TRUE,scale=TRUE)
La conclusion est la suivante. BCR est un taux de classification équilibré. Pour ce pari, plus haut est le mieux:
cat("Best model type is:",bestType,"\n")
Best model type is: 4
cat("Best cost is:",bestCost,"\n")
Best cost is: 1
cat("Best accuracy is:",bestAcc,"\n")
Best accuracy is: 0.98
print(res) yTest setosa versicolor virginica setosa 16 0 0 versicolor 0 17 0 virginica 0 3 14 print(BCR)
[1] 0.95
Forfait R - eclust
Ce package est un cluster orienté moyen pour les modèles prédictifs interprétés dans les données de haute dimension. Tout d'abord, regardons un ensemble de données appelé
simdata qui contient des données simulées pour un package:
library(eclust) data("simdata") dim(simdata)
[1] 100 502
simdata[1:5, 1:6]
YE Gene1 Gene2 Gene3 Gene4 [1,] -94.131497 0 -0.4821629 0.1298527 0.4228393 0.36643188 [2,] 7.134990 0 -1.5216289 -0.3304428 -0.4384459 1.57602830 [3,] 1.974194 0 0.7590055 -0.3600983 1.9006443 -1.47250061 [4,] -44.855010 0 0.6833635 1.8051352 0.1527713 -0.06442029 [5,] 23.547378 0 0.4587626 -0.3996984 -0.5727255 -1.75716775
table(simdata[,"E"])
0 1 50 50
La conclusion précédente montre que la dimension des données est de 100 sur 502.
Y est le vecteur de réponse continue et
E est la variable d'environnement binaire pour la méthode ECLUST.
E = 0 pour non exposé (n = 50) et
E = 1 pour exposé (n = 50).
Le programme R suivant évalue la transformée z de Fisher:
library(eclust) data("simdata") X = simdata[,c(-1,-2)] firstCorr<-cor(X[1:50,]) secondCorr<-cor(X[51:100,]) score<-u_fisherZ(n0=100,cor0=firstCorr,n1=100,cor1=secondCorr) dim(score)
[1] 500 500
score[1:5,1:5]
Gene1 Gene2 Gene3 Gene4 Gene5 Gene1 1.000000 -8.062020 6.260050 -8.133437 -7.825391 Gene2 -8.062020 1.000000 9.162208 -7.431822 -7.814067 Gene3 6.260050 9.162208 1.000000 8.072412 6.529433 Gene4 -8.133437 -7.431822 8.072412 1.000000 -5.099261 Gene5 -7.825391 -7.814067 6.529433 -5.099261 1.000000
Nous définissons la transformée z de Fisher. En supposant que nous ayons un ensemble de
n paires
x i et
y i , nous pourrions estimer leur corrélation en utilisant la formule suivante:
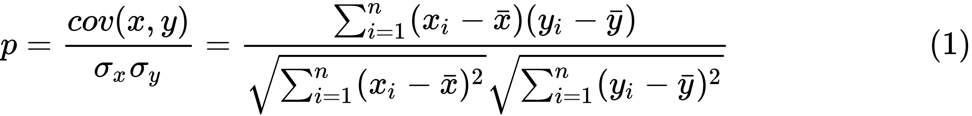
Ici
p est la corrélation entre deux variables, et

et
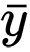
sont des moyennes d'échantillonnage pour les variables aléatoires
x et
y . La valeur de
z est définie comme:
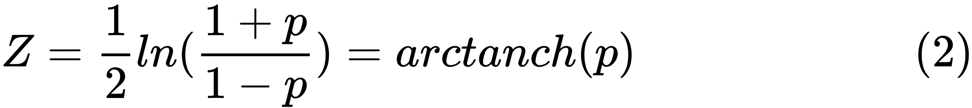 ln
ln est la fonction de logarithme naturel, et
arctanh () est la fonction tangente hyperbolique inverse.
Sélection du modèle
Lors de la recherche d'un bon modèle, nous sommes parfois confrontés à un manque / excès de données. L'exemple suivant est emprunté
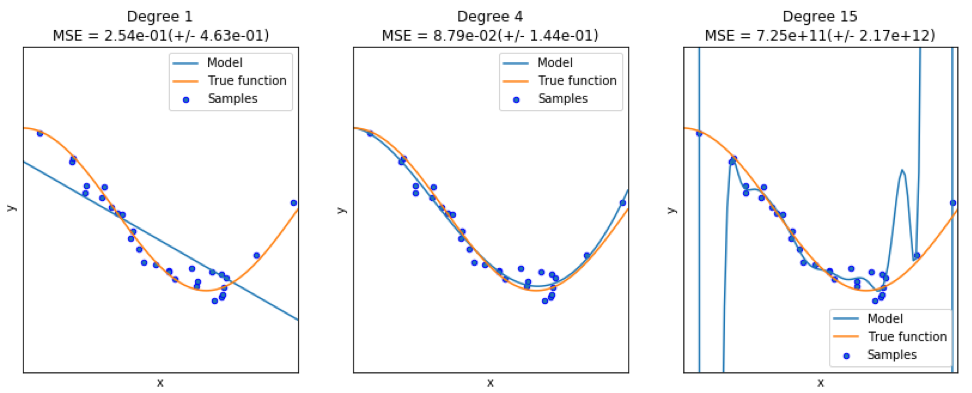
ici . Il démontre les problèmes de travailler avec cela et comment nous pouvons utiliser la régression linéaire avec des caractéristiques polynomiales pour approximer les fonctions non linéaires. Fonction spécifiée:
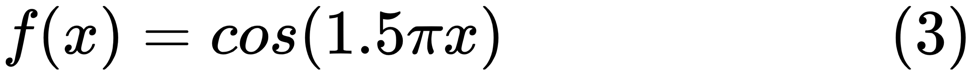
Dans le programme suivant, nous essayons d'utiliser des modèles linéaires et polynomiaux pour approximer une équation. Un code légèrement modifié est affiché ici. Le programme illustre l'effet de la pénurie / surabondance de données sur le modèle:
import sklearn import numpy as np import matplotlib.pyplot as plt from sklearn.pipeline import Pipeline from sklearn.preprocessing import PolynomialFeatures from sklearn.linear_model import LinearRegression from sklearn.model_selection import cross_val_score
Les graphiques résultants sont présentés ici:
Paquet Python - Model-Catwalk
Un exemple peut être trouvé
ici .
Les premières lignes de code sont affichées ici:
import datetime import pandas from sqlalchemy import create_engine from metta import metta_io as metta from catwalk.storage import FSModelStorageEngine, CSVMatrixStore from catwalk.model_trainers import ModelTrainer from catwalk.predictors import Predictor from catwalk.evaluation import ModelEvaluator from catwalk.utils import save_experiment_and_get_hash help(FSModelStorageEngine)
La conclusion correspondante est montrée ici. Pour économiser de l'espace, seule la partie supérieure est présentée:
Help on class FSModelStorageEngine in module catwalk.storage: class FSModelStorageEngine(ModelStorageEngine) | Method resolution order: | FSModelStorageEngine | ModelStorageEngine | builtins.object | | Methods defined here: | | __init__(self, *args, **kwargs) | Initialize self. See help(type(self)) for accurate signature. | | get_store(self, model_hash) | | ----------------------------------------------------------------------
| Data descriptors inherited from ModelStorageEngine: | | __dict__ | dictionary for instance variables (if defined) | | __weakref__ | list of weak references to the object (if defined)
Paquet Python - sklearn
Étant donné que
sklearn est un package très utile, il vaut la peine de montrer plus d'exemples d'utilisation de ce package. L'exemple donné ici montre comment utiliser le package pour classer les documents par sujet en utilisant l'approche du sac de mots.
Cet exemple utilise la matrice
scipy.sparse pour stocker des objets et illustre divers classificateurs qui peuvent traiter efficacement des matrices clairsemées. Cet exemple utilise un ensemble de données de 20 groupes de discussion. Il sera automatiquement téléchargé puis mis en cache. Le fichier zip contient des fichiers d'entrée et peut être téléchargé
ici . Le code est disponible
ici . Pour économiser de l'espace, seules les premières lignes sont affichées:
import logging import numpy as np from optparse import OptionParser import sys from time import time import matplotlib.pyplot as plt from sklearn.datasets import fetch_20newsgroups from sklearn.feature_extraction.text import TfidfVectorizer from sklearn.feature_extraction.text import HashingVectorizer from sklearn.feature_selection import SelectFromModel
La sortie correspondante est affichée ici:
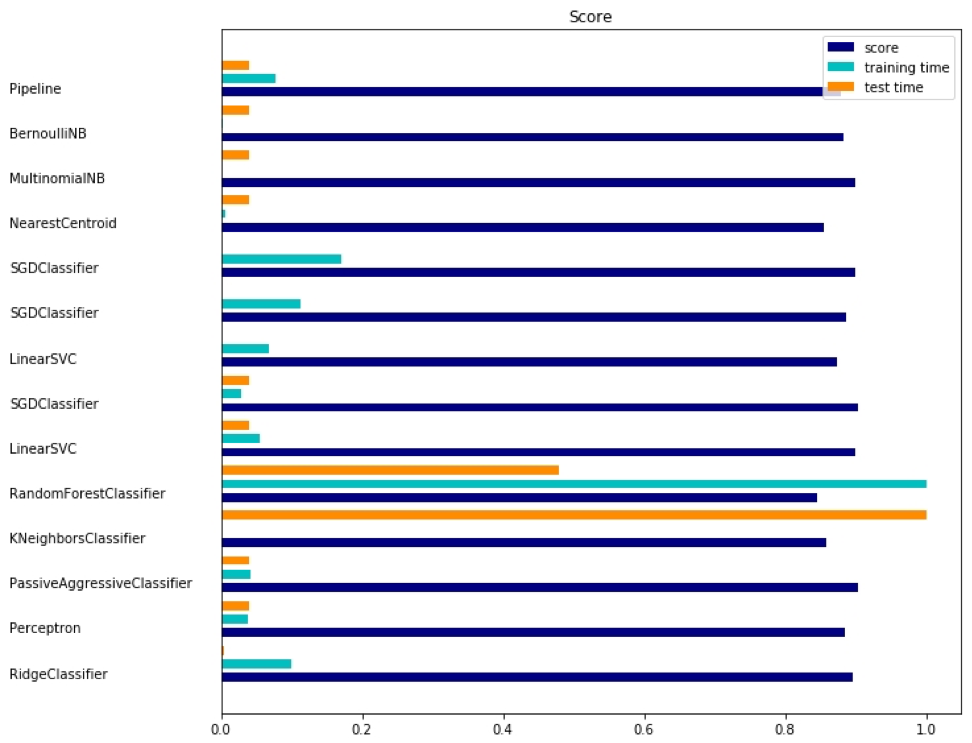
Il existe trois indicateurs pour chaque méthode: évaluation, temps de formation et temps de test.
Package Julia - QuantEcon
Prenons, par exemple, l'utilisation de chaînes de Markov:
using QuantEcon P = [0.4 0.6; 0.2 0.8]; mc = MarkovChain(P) x = simulate(mc, 100000); mean(x .== 1)
Résultat:
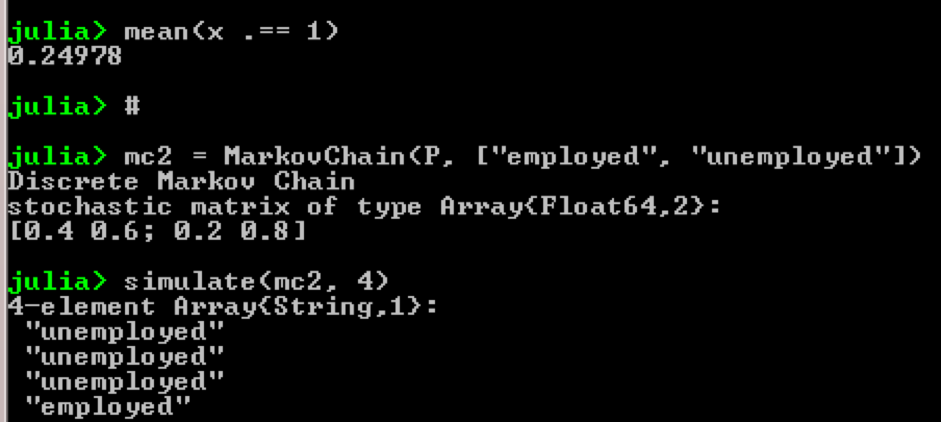
Le but de l'exemple est de voir comment une personne d'un statut économique à l'avenir se transforme en un autre. Tout d'abord, regardons le tableau suivant:
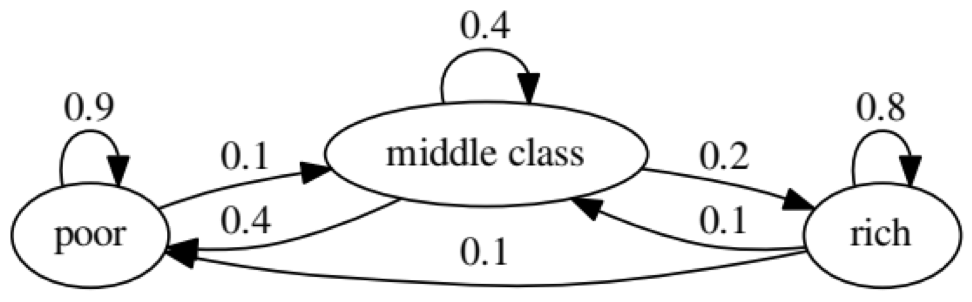
Regardons l'ovale le plus à gauche avec le statut «pauvre». 0,9 signifie qu'une personne avec ce statut a 90% de chances de rester pauvre et 10% va dans la classe moyenne. Il peut être représenté par la matrice suivante, les zéros sont là où il n'y a pas de bord entre les nœuds:
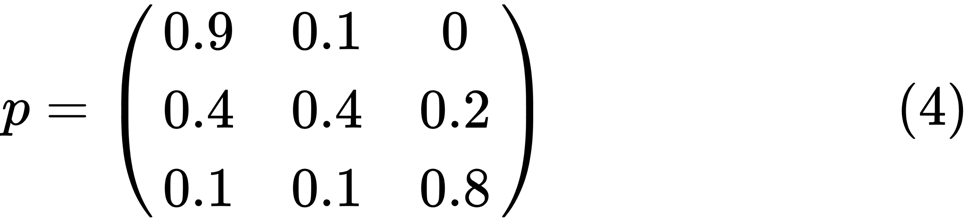
On dit que deux états, x et y, sont liés l'un à l'autre s'il y a des entiers positifs j et k, tels que:

Une chaîne de Markov
P est appelée irréductible si tous les états sont connectés; c'est-à-dire, si
x et
y sont déclarés pour chacun (x, y). Le code suivant le confirmera:
using QuantEcon P = [0.9 0.1 0.0; 0.4 0.4 0.2; 0.1 0.1 0.8]; mc = MarkovChain(P) is_irreducible(mc)
Le graphique suivant représente un cas extrême, car le statut futur d'une personne pauvre sera 100% pauvre:

Le code suivant le confirmera également, car le résultat sera
faux :
using QuantEcon P2 = [1.0 0.0 0.0; 0.1 0.8 0.1; 0.0 0.2 0.8]; mc2 = MarkovChain(P2) is_irreducible(mc2)
Test de causalité de Granger
Le test de causalité de Granger est utilisé pour déterminer si une série chronologique est un facteur et fournit des informations utiles pour prédire la seconde. Le code suivant utilise un
ensemble de données nommé
ChickEgg comme illustration. L'ensemble de données comprend deux colonnes, le nombre de poulets et le nombre d'oeufs, avec un horodatage:
library(lmtest) data(ChickEgg) dim(ChickEgg)
[1] 54 2
ChickEgg[1:5,]
chicken egg [1,] 468491 3581 [2,] 449743 3532 [3,] 436815 3327 [4,] 444523 3255 [5,] 433937 3156
La question est, pouvons-nous utiliser le nombre d'œufs cette année pour prédire le nombre de poulets l'année prochaine?
Si c'est le cas, le nombre de poulets sera la raison de Granger pour le nombre d'oeufs. Si ce n'est pas le cas, nous disons que le nombre de poulets n'est pas une raison Granger pour le nombre d'oeufs. Voici le code pertinent:
library(lmtest) data(ChickEgg) grangertest(chicken~egg, order = 3, data = ChickEgg)
Granger causality test Model 1: chicken ~ Lags(chicken, 1:3) + Lags(egg, 1:3) Model 2: chicken ~ Lags(chicken, 1:3) Res.Df Df F Pr(>F) 1 44 2 47 -3 5.405 0.002966 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Dans le modèle 1, nous essayons d'utiliser des décalages de poussins et des décalages d'oeufs pour expliquer le nombre de poussins.
Parce que la valeur de
P est assez faible (elle est significative à 0,01), nous disons que le nombre d'oeufs est la raison de Granger pour le nombre de poulets.
Le test suivant montre que les données sur les poulets ne peuvent pas être utilisées pour prédire la période suivante:
grangertest(egg~chicken, order = 3, data = ChickEgg)
Granger causality test Model 1: egg ~ Lags(egg, 1:3) + Lags(chicken, 1:3) Model 2: egg ~ Lags(egg, 1:3) Res.Df Df F Pr(>F) 1 44 2 47 -3 0.5916 0.6238
Dans l'exemple suivant, nous vérifions la rentabilité d'IBM et du S & P500 afin de découvrir qu'ils sont la raison de Granger pour un autre.
Tout d'abord, nous définissons la fonction de rendement:
ret_f<-function(x,ticker=""){ n<-nrow(x) p<-x[,6] ret<-p[2:n]/p[1:(n-1)]-1 output<-data.frame(x[2:n,1],ret) name<-paste("RET_",toupper(ticker),sep='') colnames(output)<-c("DATE",name) return(output) }
>x<-read.csv("http://canisius.edu/~yany/data/ibmDaily.csv",header=T) ibmRet<-ret_f(x,"ibm") x<-read.csv("http://canisius.edu/~yany/data/^gspcDaily.csv",header=T) mktRet<-ret_f(x,"mkt") final<-merge(ibmRet,mktRet) head(final)
DATE RET_IBM RET_MKT 1 1962-01-03 0.008742545 0.0023956877 2 1962-01-04 -0.009965497 -0.0068887673 3 1962-01-05 -0.019694350 -0.0138730891 4 1962-01-08 -0.018750380 -0.0077519519 5 1962-01-09 0.011829467 0.0004340133 6 1962-01-10 0.001798526 -0.0027476933
Maintenant, la fonction peut être appelée avec des valeurs d'entrée. L'objectif du programme est de tester si nous pouvons utiliser les décalages du marché pour expliquer la rentabilité d'IBM. De la même manière, nous vérifions pour expliquer le retard d'IBM dans les revenus du marché:
library(lmtest) grangertest(RET_IBM ~ RET_MKT, order = 1, data =final)
Granger causality test Model 1: RET_IBM ~ Lags(RET_IBM, 1:1) + Lags(RET_MKT, 1:1) Model 2: RET_IBM ~ Lags(RET_IBM, 1:1) Res.Df Df F Pr(>F) 1 14149 2 14150 -1 24.002 9.729e-07 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Les résultats montrent que le S & P500 peut être utilisé pour expliquer la rentabilité d'IBM pour la prochaine période, car il est statistiquement significatif à 0,1%. Le code suivant vérifiera si le décalage d'IBM explique le changement dans le S & P500:
grangertest(RET_MKT ~ RET_IBM, order = 1, data =final)
Granger causality test Model 1: RET_MKT ~ Lags(RET_MKT, 1:1) + Lags(RET_IBM, 1:1) Model 2: RET_MKT ~ Lags(RET_MKT, 1:1) Res.Df Df F Pr(>F) 1 14149 2 14150 -1 7.5378 0.006049 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Le résultat suggère que pendant cette période, les rendements d'IBM peuvent être utilisés pour expliquer l'indice S & P500 pour la période suivante.