Présentation de la méthode de vecteur de référence d'algorithme d'apprentissage automatique (SVM)

Préface

Dans cet article, nous explorerons plusieurs aspects de SVM:

• composante théorique de SVM;
• comment l'algorithme fonctionne sur des échantillons qui ne peuvent pas être divisés en classes de façon linéaire;
• Exemple Python et implémentation de l'algorithme dans la bibliothèque SciKit Learn.

Dans les articles suivants, je vais essayer de parler de la composante mathématique de cet algorithme.

Comme vous le savez, les tâches d'apprentissage automatique sont divisées en deux catégories principales: la classification et la régression. En fonction de laquelle de ces tâches nous sommes confrontés et de l'ensemble de données dont nous disposons pour cette tâche, nous choisissons l'algorithme à utiliser.

La méthode Support Vector Machines ou SVM (de l'anglais Support Vector Machines) est un algorithme linéaire utilisé dans les problèmes de classification et de régression. Cet algorithme est largement utilisé dans la pratique et peut résoudre à la fois des problèmes linéaires et non linéaires. L'essence des «Machines» des vecteurs de support est simple: l'algorithme crée une ligne ou un hyperplan qui divise les données en classes.

Théorie

La tâche principale de l'algorithme est de trouver la ligne ou l'hyperplan le plus correct, en divisant les données en deux classes. SVM est un algorithme qui reçoit des données à l'entrée et renvoie une telle ligne de division.

Prenons l'exemple suivant. Supposons que nous ayons un ensemble de données et que nous voulons classer et séparer les carrés rouges des cercles bleus (disons positifs et négatifs). Le but principal de cette tâche sera de trouver la ligne «idéale» qui séparera ces deux classes.



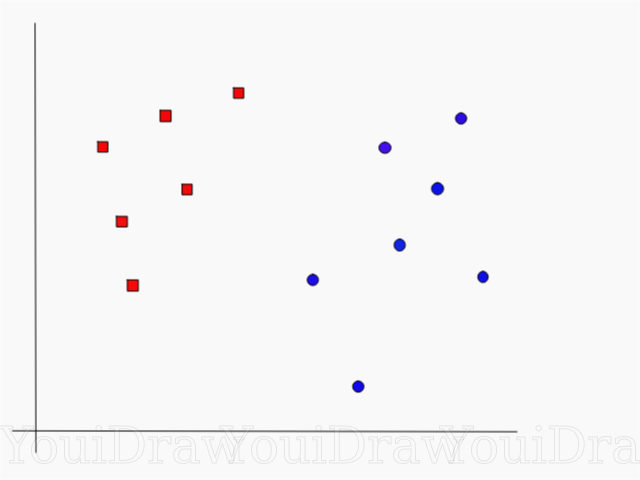
Trouvez la ligne ou l'hyperplan parfait qui divise l'ensemble de données en classes bleues et rouges.

À première vue, ce n'est pas si difficile, non?

Mais, comme vous pouvez le voir, il n'y a pas de ligne unique qui résoudrait un tel problème. Nous pouvons prendre un nombre infini de lignes qui peuvent séparer ces deux classes. Comment SVM trouve-t-il exactement la ligne «idéale» et qu'est-ce qui est «idéal» dans sa compréhension?

Jetez un œil à l'exemple ci-dessous et pensez à laquelle des deux lignes (jaune ou verte) sépare le mieux les deux classes, et correspond à la description de «idéal»?



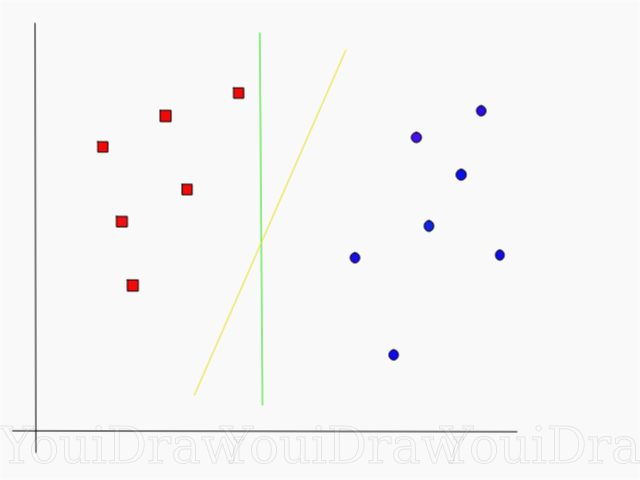
Selon vous, quelle ligne sépare mieux l'ensemble de données?

Si vous avez choisi la ligne jaune, je vous félicite: c'est la ligne que l'algorithme choisirait. Dans cet exemple, nous pouvons comprendre intuitivement que la ligne jaune sépare et classe en conséquence les deux classes mieux que la verte.

Dans le cas de la ligne verte - elle est située trop près de la classe rouge. Malgré le fait qu'elle ait correctement classé tous les objets de l'ensemble de données actuel, une telle ligne ne sera pas généralisée - elle ne se comportera pas aussi bien avec un ensemble de données inconnu. La tâche de trouver une généralisation séparant deux classes est l'une des tâches principales de l'apprentissage automatique.

Comment SVM trouve la meilleure ligne

L'algorithme SVM est conçu de manière à rechercher des points sur le graphique qui sont situés directement sur la ligne de séparation la plus proche. Ces points sont appelés vecteurs de référence. Ensuite, l'algorithme calcule la distance entre les vecteurs de support et le plan de division. C'est la distance appelée l'écart. L'objectif principal de l'algorithme est de maximiser la distance de dégagement. Le meilleur hyperplan est considéré comme un hyperplan pour lequel cet écart est le plus grand possible.



Assez simple, non? Prenons l'exemple suivant, avec un ensemble de données plus complexe qui ne peut pas être divisé linéairement.



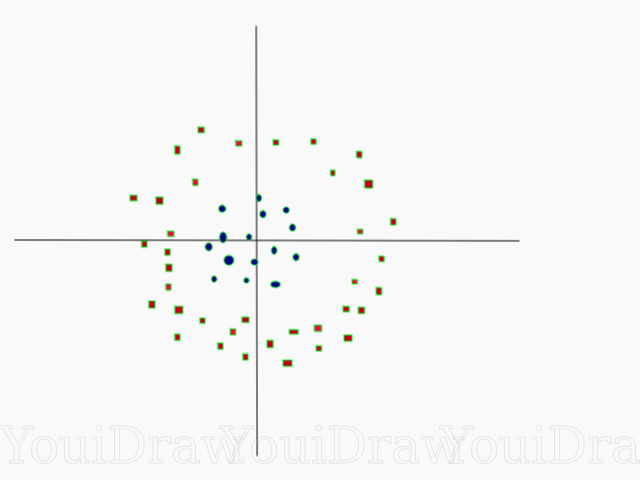
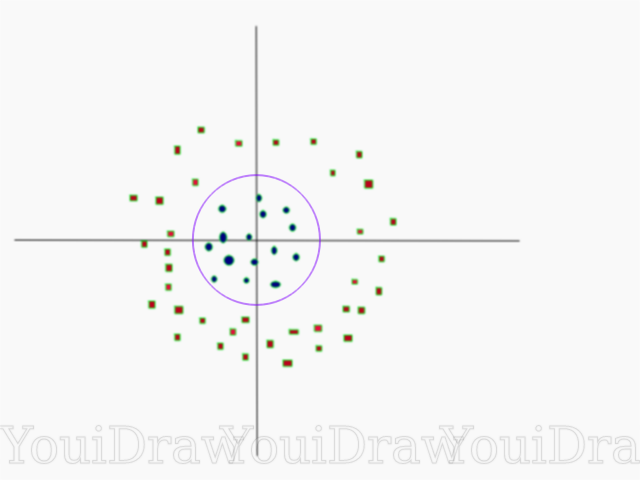
De toute évidence, cet ensemble de données ne peut pas être divisé de façon linéaire. Nous ne pouvons pas tracer une ligne droite qui classerait ces données. Mais, cet ensemble de données peut être divisé linéairement, en ajoutant une dimension supplémentaire, que nous appellerons l'axe Z. Imaginez que les coordonnées sur l'axe Z soient régulées par la restriction suivante:

$$

$$z = x² + y²$$

Ainsi, l'ordonnée Z est représentée à partir du carré de la distance du point au début de l'axe.
Ci-dessous, une visualisation du même jeu de données sur l'axe Z.



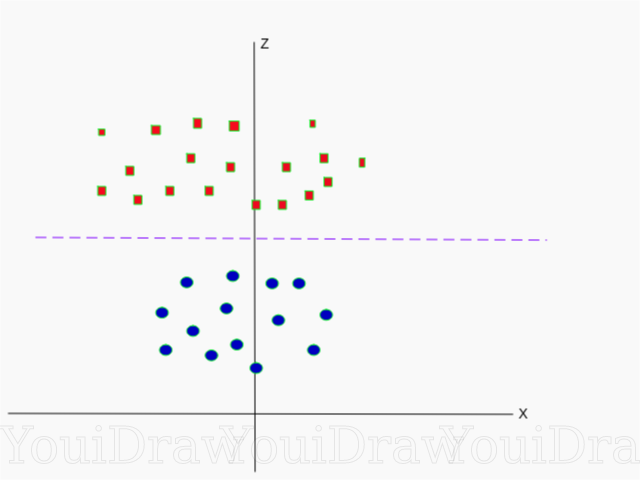
Maintenant, les données peuvent être divisées linéairement. Supposons que la ligne magenta séparant les données z = k, où k est une constante. Si

$$

$$z = x² + y²$$

alors

$$

$$k = x² + y²$$

- formule du cercle. Ainsi, nous pouvons projeter notre diviseur linéaire, revenir au nombre d'origine de dimensions d'échantillon, en utilisant cette transformation.



Par conséquent, nous pouvons classer un ensemble de données non linéaire en lui ajoutant une dimension supplémentaire, puis le ramener à sa forme d'origine à l'aide de la transformation mathématique. Cependant, pas avec tous les ensembles de données, il est tout aussi facile de lancer une telle transformation. Heureusement, l'implémentation de cet algorithme dans la bibliothèque sklearn résout ce problème pour nous.

Hyperplan

Maintenant que nous nous sommes familiarisés avec la logique de l'algorithme, nous passons à la définition formelle d'un hyperplan

Un hyperplan est un sous-plan de dimension n-1 dans un espace euclidien à n dimensions qui divise l'espace en deux parties distinctes.

Par exemple, imaginez que notre ligne est représentée comme un espace euclidien unidimensionnel (c'est-à-dire que notre ensemble de données se trouve sur une ligne droite). Sélectionnez un point sur cette ligne. Ce point divisera l'ensemble de données, dans notre cas la ligne, en deux parties. La ligne a une mesure et le point a 0 mesure. Par conséquent, un point est un hyperplan d'une ligne.

Pour l'ensemble de données bidimensionnel que nous avons rencontré précédemment, la ligne de démarcation était le même hyperplan. Autrement dit, pour un espace à n dimensions, il y a un hyperplan à n dimensions qui divise cet espace en deux parties.

CODE

import numpy as np X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]]) y = np.array([1, 1, 2, 2]) 

Les points sont représentés comme un tableau de X et les classes auxquelles ils appartiennent comme un tableau de y.
Nous allons maintenant former notre modèle avec cet échantillon. Pour cet exemple, j'ai défini le paramètre linéaire du «noyau» du classificateur (noyau).

 from sklearn.svm import SVC clf = SVC(kernel='linear') clf = SVC.fit(X, y) 

Prédiction de classe d'un nouvel objet

 prediction = clf.predict([[0,6]]) 

Réglage des paramètres

Les paramètres sont les arguments que vous transmettez lors de la création du classificateur. Ci-dessous, j'ai fourni certains des paramètres SVM personnalisés les plus importants:

"C"

Ce paramètre permet d'ajuster cette fine ligne entre la «douceur» et la précision de la classification des objets dans l'échantillon d'apprentissage. Plus la valeur «C» est élevée, plus les objets de l'ensemble d'apprentissage seront correctement classés.



Dans cet exemple, il existe plusieurs seuils de décision que nous pouvons définir pour cet échantillon particulier. Faites attention au seuil de décision direct (présenté sur le graphique comme une ligne verte). C'est assez simple, et pour cette raison, plusieurs objets ont été mal classés. Ces points qui ont été mal classés sont appelés valeurs aberrantes dans les données.

Nous pouvons également ajuster les paramètres de telle manière qu'à la fin, nous obtenons une ligne plus courbe (seuil de décision bleu clair), qui classera absolument toutes les données de l'échantillon d'apprentissage correctement. Bien sûr, dans ce cas, les chances que notre modèle soit en mesure de généraliser et d'afficher des résultats tout aussi bons sur de nouvelles données sont catastrophiques. Par conséquent, si vous essayez d'atteindre la précision lors de la formation du modèle, vous devez viser quelque chose de plus uniforme, direct. Plus le nombre «C» est élevé, plus l'hyperplan est enchevêtré dans votre modèle, mais plus le nombre d'objets correctement classés dans l'ensemble d'apprentissage est élevé. Par conséquent, il est important de «tordre» les paramètres du modèle pour un ensemble de données spécifique afin d'éviter de se recycler mais, en même temps, d'atteindre une grande précision.

Gamma

Dans la documentation officielle, la bibliothèque SciKit Learn indique que le gamma détermine dans quelle mesure chacun des éléments de l'ensemble de données a une influence sur la détermination de la «ligne idéale». Plus le gamma est bas, plus les éléments, même ceux qui sont suffisamment éloignés de la ligne de démarcation, participent au processus de choix de cette même ligne. Si le gamma est élevé, l'algorithme ne «s'appuiera» que sur les éléments les plus proches de la ligne elle-même.
Si le niveau gamma est trop élevé, seuls les éléments les plus proches de la ligne participeront au processus décisionnel sur l'emplacement de la ligne. Cela aidera à ignorer les valeurs aberrantes dans les données. L'algorithme SVM est conçu pour que les points situés les plus proches les uns des autres aient plus de poids lors de la prise de décision. Cependant, avec le réglage correct de "C" et "gamma", un résultat optimal peut être obtenu qui construira un hyperplan plus linéaire qui ignore les valeurs aberrantes et, par conséquent, est plus généralisable.

Conclusion

J'espère sincèrement que cet article vous a aidé à comprendre l'essence du travail de SVM ou de la méthode des vecteurs de référence. J'attends de vous tout commentaire et conseil. Dans des publications ultérieures, je parlerai de la composante mathématique de SVM et des problèmes d'optimisation.

Sources:
Documentation SVM officielle dans SciKit Learn
Vers le blog DataScience
Siraj Raval: Support des machines à vecteurs
Intro to Machine Learning Udacity SVM: Vidéo du cours Gamma
Wikipédia: SVM