Source : Wikipedia License CC-BY-SA 3.0

Si vous voyagez souvent en transports en commun, vous êtes probablement tombé sur cette situation:

Vous arrêtez. Il est écrit que le bus circule toutes les 10 minutes. Notez l'heure ... Enfin, après 11 minutes, le bus arrive et la pensée: pourquoi suis-je toujours malchanceux?

En théorie, si les bus arrivent toutes les 10 minutes et que vous arrivez à une heure aléatoire, l'attente moyenne devrait être d'environ 5 minutes. Mais en réalité, les bus n'arrivent pas à l'heure, vous pouvez donc attendre plus longtemps. Il s'avère que, avec quelques hypothèses raisonnables, on peut arriver à une conclusion surprenante:

Lorsque vous attendez un bus qui arrive en moyenne toutes les 10 minutes, votre temps d'attente moyen sera de 10 minutes.

C'est ce que l'on appelle parfois le paradoxe du temps d'attente .

J'avais une idée avant, et je me suis toujours demandé si c'était vraiment vrai ... dans quelle mesure ces «hypothèses raisonnables» correspondent-elles à la réalité? Dans cet article, nous examinons le paradoxe de la latence en termes de modélisation et d'arguments probabilistes, puis examinons certaines des données de bus réelles à Seattle pour (espérons-le) résoudre le paradoxe une fois pour toutes.

Inspection Paradox

Si les bus arrivent exactement toutes les dix minutes, le temps d'attente moyen sera de 5 minutes. On peut facilement comprendre pourquoi l'ajout de variations à l'intervalle entre les bus augmente le temps d'attente moyen.

Le paradoxe du temps d’attente est un cas particulier d’un phénomène plus général - le paradoxe de l’inspection , qui est examiné en détail dans l’article sensible d’Allen Downey, «Le paradoxe de l’inspection partout autour de nous» .

Bref, le paradoxe de l'inspection se pose chaque fois que la probabilité d'observer une quantité est liée à la quantité observée. Allen donne un exemple d'enquête auprès des étudiants universitaires sur la taille moyenne de leurs classes. Bien que l'école parle honnêtement du nombre moyen de 30 élèves par groupe, la taille moyenne du groupe du point de vue des élèves est beaucoup plus grande. La raison en est que dans les grandes classes (naturellement) il y a plus d'élèves, ce qui est révélé lors de leur enquête.

Dans le cas d'un horaire de bus avec un intervalle déclaré de 10 minutes, parfois l'intervalle entre les arrivées est supérieur à 10 minutes, et parfois plus court. Et si vous vous arrêtez à un moment aléatoire, vous êtes plus susceptible de rencontrer un intervalle plus long qu'un intervalle plus court. Il est donc logique que l'intervalle de temps moyen entre les intervalles d' attente soit plus long que l'intervalle de temps moyen entre les bus, car les intervalles plus longs sont plus courants dans l'échantillon.

Mais le paradoxe de la latence fait une déclaration plus forte: si l'espacement moyen des bus est $$$N$ minutes, le temps d'attente moyen des passagers est $$$2N$ minutes. Serait-ce vrai?

Simulation de latence

Pour nous convaincre du caractère raisonnable de cela, nous simulons d'abord le flux des bus qui arrivent en moyenne 10 minutes. Pour plus de précision, prenez un grand échantillon: un million de bus (soit environ 19 ans de trafic continu pendant 10 minutes):

import numpy as np N = 1000000 # number of buses tau = 10 # average minutes between arrivals rand = np.random.RandomState(42) # universal random seed bus_arrival_times = N * tau * np.sort(rand.rand(N)) 

Vérifier que l'intervalle moyen est proche de $$$\ tau = 10$ :

 intervals = np.diff(bus_arrival_times) intervals.mean() 

9.9999879601518398

Maintenant, nous pouvons simuler l'arrivée d'un grand nombre de passagers à un arrêt de bus pendant cette période et calculer le temps d'attente que chacun d'eux connaît. Encapsulez le code dans une fonction pour une utilisation ultérieure:

 def simulate_wait_times(arrival_times, rseed=8675309, # Jenny's random seed n_passengers=1000000): rand = np.random.RandomState(rseed) arrival_times = np.asarray(arrival_times) passenger_times = arrival_times.max() * rand.rand(n_passengers) # find the index of the next bus for each simulated passenger i = np.searchsorted(arrival_times, passenger_times, side='right') return arrival_times[i] - passenger_times 

Ensuite, nous simulons le temps d'attente et calculons la moyenne:

 wait_times = simulate_wait_times(bus_arrival_times) wait_times.mean() 

10.001584206227317

Le temps d'attente moyen est proche de 10 minutes, comme le prédit le paradoxe.

Creuser plus profondément: probabilités et processus de Poisson

Comment simuler une telle situation?

En fait, il s'agit d'un exemple de paradoxe d'inspection, où la probabilité d'observer une valeur est liée à la valeur elle-même. Désigner par $$$p (T)$ espacement $$$T$ entre les bus lorsqu'ils arrivent à l'arrêt de bus. Dans un tel enregistrement, la valeur attendue de l'heure d'arrivée sera:

$$

$$E [T] = \ int_0 ^ \ infty T ~ p (T) ~ dT$$

Dans la simulation précédente, nous avons sélectionné $$$E [T] = \ tau = 10$ minutes.

Lorsqu'un passager arrive à un arrêt de bus à tout moment, la probabilité de temps d'attente dépend non seulement de $$$p (T)$ mais aussi de $$$T$ : plus l'intervalle est grand, plus il y a de passagers.

Ainsi, nous pouvons écrire la distribution de l'heure d'arrivée du point de vue des passagers:

$$

$$p_ {exp} (T) \ propto T ~ p (T)$$

La constante de proportionnalité est dérivée de la normalisation de la distribution:

$$

$$p_ {exp} (T) = \ frac {T ~ p (T)} {\ int_0 ^ \ infty T ~ p (T) ~ dT}$$

Il simplifie

$$

$$p_ {exp} (T) = \ frac {T ~ p (T)} {E [T]}$$

Puis le temps d'attente $$$E [W]$ sera la moitié de l'intervalle prévu pour les passagers, afin que nous puissions enregistrer

$$

$$E [W] = \ frac {1} {2} E_ {exp} [T] = \ frac {1} {2} \ int_0 ^ \ infty T ~ p_ {exp} (T) ~ dT$$

qui peut être réécrit de manière plus compréhensible:

$$

$$E [W] = \ frac {E [T ^ 2]} {2E [T]}$$

et maintenant il ne reste plus qu'à choisir une forme pour $$$p (T)$ et calculer les intégrales.

Le choix de p (T)

Ayant reçu un modèle formel, quelle est une distribution raisonnable pour $$$p (T)$ ? Nous allons dessiner une image de la distribution $$$p (T)$ au sein de nos arrivées simulées en traçant un histogramme des intervalles entre les arrivées:

 %matplotlib inline import matplotlib.pyplot as plt plt.style.use('seaborn') plt.hist(intervals, bins=np.arange(80), density=True) plt.axvline(intervals.mean(), color='black', linestyle='dotted') plt.xlabel('Interval between arrivals (minutes)') plt.ylabel('Probability density'); 

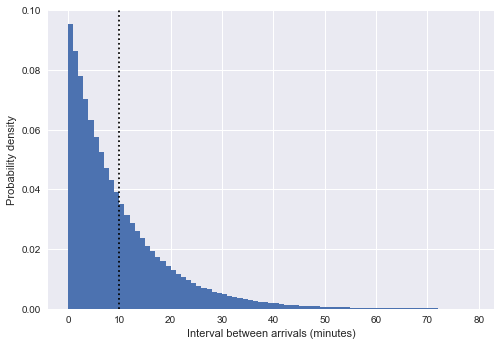
Ici, la ligne pointillée verticale montre un intervalle moyen d'environ 10 minutes. Ceci est très similaire à une distribution exponentielle, et non par accident: notre simulation de l'heure d'arrivée du bus sous forme de nombres aléatoires uniformes est très proche du processus de Poisson , et pour un tel processus, la distribution des intervalles est exponentielle.

(Remarque: dans notre cas, il ne s'agit que d'un exposant approximatif; en fait, les intervalles $$$T$ entre $$$N$ points uniformément sélectionnés dans un laps de temps $$$N \ tau$ correspondre à la distribution bêta $$$T / (N \ tau) \ sim \ mathrm {Beta} [1, N]$ qui est dans la grande limite $$$N$ approchant $$$T \ sim \ mathrm {Exp} [1 / \ tau]$ . Pour plus d'informations, vous pouvez lire, par exemple, un article sur StackExchange ou ce fil sur Twitter ).

La distribution exponentielle des intervalles implique que l'heure d'arrivée suit le processus de Poisson. Pour vérifier ce raisonnement, nous vérifions la présence d'une autre propriété du processus de Poisson: que le nombre d'arrivées sur une période de temps fixe est une distribution de Poisson. Pour ce faire, nous divisons les arrivées simulées en blocs de temps:

 from scipy.stats import poisson # count the number of arrivals in 1-hour bins binsize = 60 binned_arrivals = np.bincount((bus_arrival_times // binsize).astype(int)) x = np.arange(20) # plot the results plt.hist(binned_arrivals, bins=x - 0.5, density=True, alpha=0.5, label='simulation') plt.plot(x, poisson(binsize / tau).pmf(x), 'ok', label='Poisson prediction') plt.xlabel('Number of arrivals per hour') plt.ylabel('frequency') plt.legend(); 

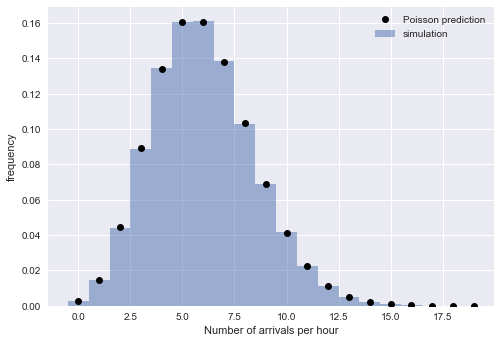
La correspondance étroite des valeurs empiriques et théoriques nous convainc de la justesse de notre interprétation: pour les grands $$$N$ L'heure d'arrivée simulée est bien décrite par le processus de Poisson, qui implique des intervalles distribués exponentiellement.

Cela signifie que la distribution de probabilité peut s'écrire:

$$

$$p (T) = \ frac {1} {\ tau} e ^ {- T / \ tau}$$

Si nous substituons le résultat dans la formule précédente, nous trouverons le temps d'attente moyen pour les passagers à l'arrêt:

$$

$$E [W] = \ frac {\ int_0 ^ \ infty T ^ 2 ~ e ^ {- T / \ tau}} {2 \ int_0 ^ \ infty T ~ e ^ {- T / \ tau}} = \ frac {2 \ tau ^ 3} {2 (\ tau ^ 2)} = \ tau$$

Pour les vols avec arrivées via le processus de Poisson, le temps d'attente attendu est identique à l'intervalle moyen entre les arrivées.

Ce problème peut être argumenté comme suit: le processus de Poisson est un processus sans mémoire , c'est-à-dire que l'histoire des événements n'a rien à voir avec l'heure attendue de l'événement suivant. Par conséquent, à l'arrivée à un arrêt de bus, le temps d'attente moyen pour un bus est toujours le même: dans notre cas, il est de 10 minutes, quel que soit le temps écoulé depuis le bus précédent! Peu importe combien de temps vous avez attendu: le temps prévu pour le prochain bus est toujours exactement 10 minutes: dans le processus de Poisson, vous n'obtenez pas de «crédit» pour le temps passé à attendre.

Expiration de la réalité

Ce qui précède est bon si les arrivées réelles de bus sont réellement décrites par le processus de Poisson, mais est-ce le cas?


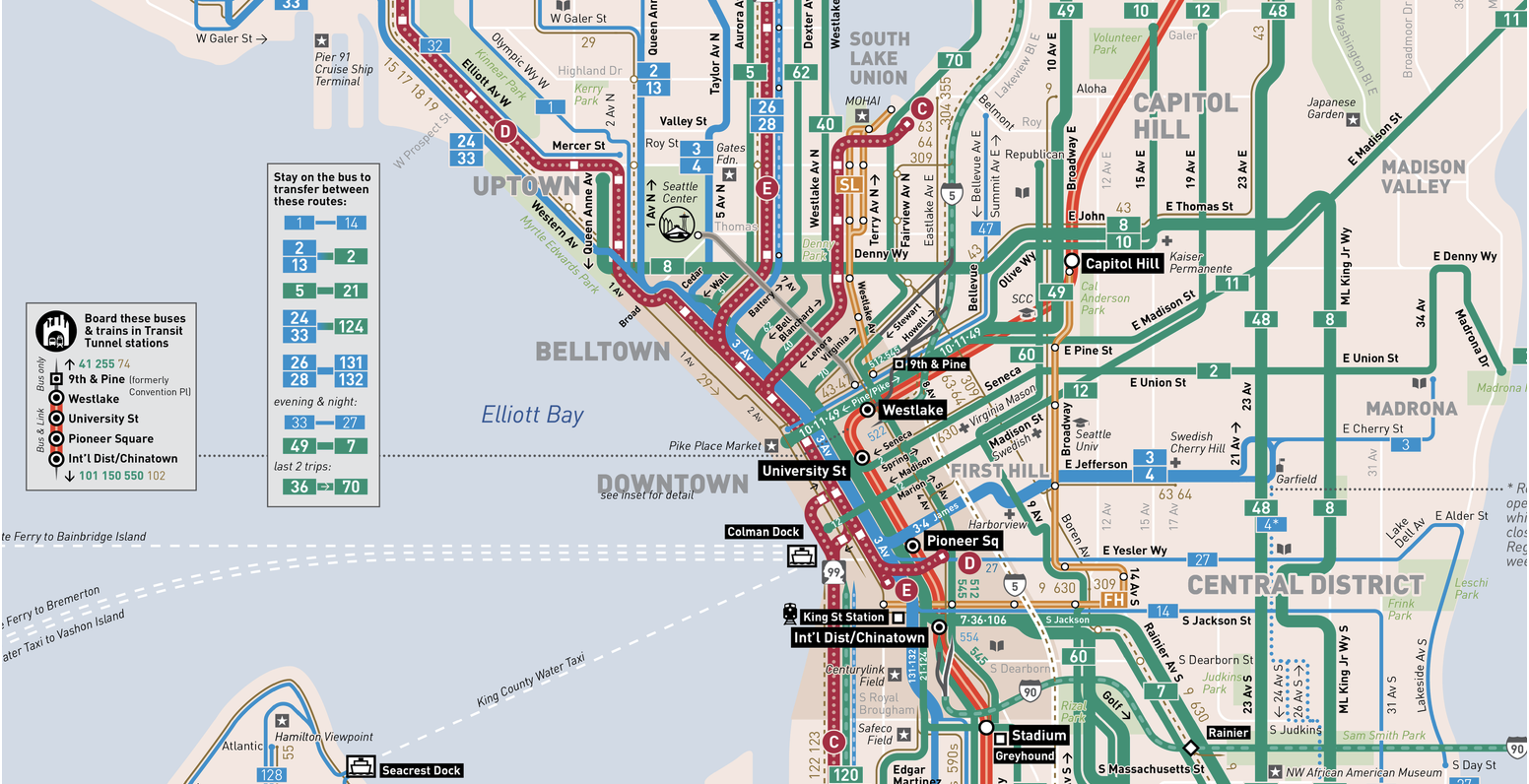Source: Régime de transports publics de Seattle

Essayons de déterminer comment le paradoxe du temps d'attente est cohérent avec la réalité. Pour ce faire, nous allons examiner certaines des données disponibles en téléchargement ici: Arrival_times.csv (fichier CSV de 3 Mo). L'ensemble de données contient les heures d'arrivée prévues et réelles pour les bus RapidRide C, D et E à la 3e et Pike Bus Stop au centre-ville de Seattle. Les données ont été enregistrées au deuxième trimestre de 2016 (un grand merci à Mark Hallenback du Washington State Transportation Center pour ce fichier!).

 import pandas as pd df = pd.read_csv('arrival_times.csv') df = df.dropna(axis=0, how='any') df.head() 

	OPD_DATE	VEHICLE_ID	RTE	DIR	TRIP_ID	STOP_ID	STOP_NAME	SCH_STOP_TM	ACT_STOP_TM
0	2016-03-26	6201	673	S	30908177	431	3E AVE ET PIKE ST (431)	01:11:57	01:13:19
1	2016-03-26	6201	673	S	30908033	431	3E AVE ET PIKE ST (431)	23:19:57	23:16:13
2	2016-03-26	6201	673	S	30908028	431	3E AVE ET PIKE ST (431)	21:19:57	21:18:46
3	2016-03-26	6201	673	S	30908019	431	3E AVE ET PIKE ST (431)	19:04:57	19:01:49
4	2016-03-26	6201	673	S	30908252	431	3E AVE ET PIKE ST (431)	16:42:57	16:42:39

J'ai choisi les données RapidRide, notamment parce que pour la plupart de la journée, les bus circulent à intervalles réguliers de 10 à 15 minutes, sans parler du fait que je suis un passager fréquent de l'itinéraire C.

Nettoyage des données

Tout d'abord, nous ferons un petit nettoyage des données pour les convertir en une vue pratique:

 # combine date and time into a single timestamp df['scheduled'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['SCH_STOP_TM']) df['actual'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['ACT_STOP_TM']) # if scheduled & actual span midnight, then the actual day needs to be adjusted minute = np.timedelta64(1, 'm') hour = 60 * minute diff_hrs = (df['actual'] - df['scheduled']) / hour df.loc[diff_hrs > 20, 'actual'] -= 24 * hour df.loc[diff_hrs < -20, 'actual'] += 24 * hour df['minutes_late'] = (df['actual'] - df['scheduled']) / minute # map internal route codes to external route letters df['route'] = df['RTE'].replace({673: 'C', 674: 'D', 675: 'E'}).astype('category') df['direction'] = df['DIR'].replace({'N': 'northbound', 'S': 'southbound'}).astype('category') # extract useful columns df = df[['route', 'direction', 'scheduled', 'actual', 'minutes_late']].copy() df.head() 

	Parcours	Direction	Graphique	Fait arrivée	Retard (min)
0	C	sud	2016-03-26 01:11:57	2016-03-26 01:13:19	1,366667
1	C	sud	2016-03-26 23:19:57	2016-03-26 23:16:13	-3,733333
2	C	sud	2016-03-26 21:19:57	2016-03-26 21:18:46	-1.183333
3	C	sud	2016-03-26 19:04:57	2016-03-26 19:01:49	-3.133333
4	C	sud	2016-03-26 16:42:57	2016-03-26 16:42:39	-0,300000

À quelle heure sont les bus?

Ce tableau contient six ensembles de données: les directions nord et sud pour chaque itinéraire C, D et E. Pour avoir une idée de leurs caractéristiques, construisons un histogramme de l'heure d'arrivée réelle réelle moins pour chacun de ces six:

 import seaborn as sns g = sns.FacetGrid(df, row="direction", col="route") g.map(plt.hist, "minutes_late", bins=np.arange(-10, 20)) g.set_titles('{col_name} {row_name}') g.set_axis_labels('minutes late', 'number of buses'); 

Il est logique de supposer que les bus sont plus proches de l'horaire au début de l'itinéraire et s'en écartent davantage vers la fin. Les données le confirment: notre arrêt sur la route sud C, ainsi que sur le nord D et E est proche du début de la route, et en sens inverse, non loin de la destination finale.

Intervalles planifiés et observés

Jetez un œil aux intervalles de bus observés et prévus pour ces six itinéraires. Commençons par la fonction groupby dans Pandas pour calculer ces intervalles:

 def compute_headway(scheduled): minute = np.timedelta64(1, 'm') return scheduled.sort_values().diff() / minute grouped = df.groupby(['route', 'direction']) df['actual_interval'] = grouped['actual'].transform(compute_headway) df['scheduled_interval'] = grouped['scheduled'].transform(compute_headway) 

 g = sns.FacetGrid(df.dropna(), row="direction", col="route") g.map(plt.hist, "actual_interval", bins=np.arange(50) + 0.5) g.set_titles('{col_name} {row_name}') g.set_axis_labels('actual interval (minutes)', 'number of buses'); 

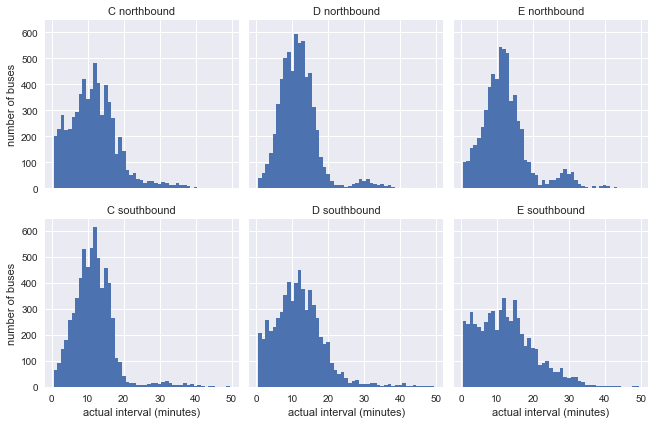
Il est déjà évident que les résultats ne sont pas très similaires à la distribution exponentielle de notre modèle, mais cela ne dit toujours rien: les distributions peuvent être affectées par des intervalles incohérents dans le graphique.

Répétons la construction des diagrammes en prenant les intervalles d'arrivée prévus plutôt que les observés:

 g = sns.FacetGrid(df.dropna(), row="direction", col="route") g.map(plt.hist, "scheduled_interval", bins=np.arange(20) - 0.5) g.set_titles('{col_name} {row_name}') g.set_axis_labels('scheduled interval (minutes)', 'frequency'); 

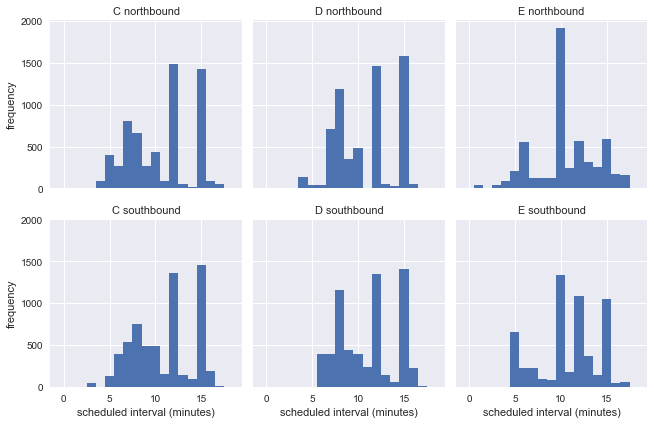
Cela montre que pendant la semaine, les bus circulent à différents intervalles, nous ne pouvons donc pas estimer la précision du paradoxe du temps d'attente à partir des informations réelles de l'arrêt.

Construire des horaires uniformes

Bien que l'horaire officiel ne donne pas d'intervalles uniformes, il existe plusieurs intervalles de temps spécifiques avec un grand nombre de bus: par exemple, près de 2 000 bus de l'itinéraire E en direction du nord avec un intervalle prévu de 10 minutes. Pour savoir si le paradoxe de latence est applicable, regroupons les données en itinéraires, directions et intervalle prévu, puis ré-empilons-les comme si elles s'étaient produites séquentiellement. Cela devrait préserver toutes les caractéristiques pertinentes des données sources, tout en facilitant la comparaison directe avec les prédictions du paradoxe de latence.

 def stack_sequence(data): # first, sort by scheduled time data = data.sort_values('scheduled') # re-stack data & recompute relevant quantities data['scheduled'] = data['scheduled_interval'].cumsum() data['actual'] = data['scheduled'] + data['minutes_late'] data['actual_interval'] = data['actual'].sort_values().diff() return data subset = df[df.scheduled_interval.isin([10, 12, 15])] grouped = subset.groupby(['route', 'direction', 'scheduled_interval']) sequenced = grouped.apply(stack_sequence).reset_index(drop=True) sequenced.head() 

	Parcours	Direction	Horaire	Fait arrivée	Retard (min)	Fait intervalle	Intervalle planifié
0	C	au nord	10,0	12.400000	2 400 000	NaN	10,0
1	C	au nord	20,0	27.150000	7.150000	0,183333	10,0
2	C	au nord	30,0	26.966667	-3.033333	14.566667	10,0
3	C	au nord	40,0	35.516667	-4.483333	8.366667	10,0
4	C	au nord	50,0	53,583333	3,583333	18.066667	10,0

Sur les données effacées, vous pouvez faire un graphique de la distribution de l'apparence réelle des bus le long de chaque itinéraire et direction avec une fréquence d'arrivée:

 for route in ['C', 'D', 'E']: g = sns.FacetGrid(sequenced.query(f"route == '{route}'"), row="direction", col="scheduled_interval") g.map(plt.hist, "actual_interval", bins=np.arange(40) + 0.5) g.set_titles('{row_name} ({col_name:.0f} min)') g.set_axis_labels('actual interval (min)', 'count') g.fig.set_size_inches(8, 4) g.fig.suptitle(f'{route} line', y=1.05, fontsize=14) 

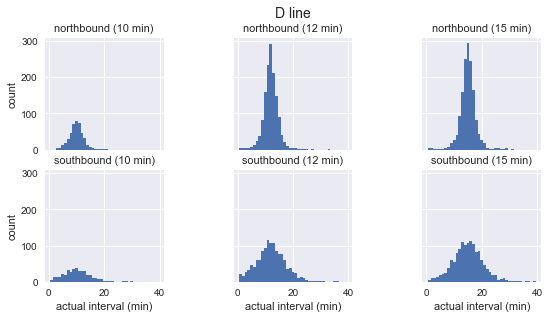
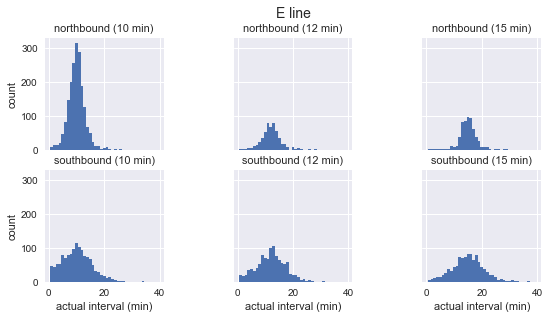
On voit que pour chaque route la distribution des intervalles observés est presque gaussienne. Il culmine près de l'intervalle prévu et présente un écart-type moins important au début de l'itinéraire (sud pour C, nord pour D / E) et plus à la fin. Même à vue, les intervalles d'arrivée réels ne correspondent certainement pas à la distribution exponentielle, qui est l'hypothèse principale sur laquelle se fonde le paradoxe du temps d'attente.

Nous pouvons utiliser la fonction de simulation du temps d'attente que nous avons utilisée ci-dessus pour trouver le temps d'attente moyen pour chaque ligne de bus, direction et horaire:

 grouped = sequenced.groupby(['route', 'direction', 'scheduled_interval']) sims = grouped['actual'].apply(simulate_wait_times) sims.apply(lambda times: "{0:.1f} +/- {1:.1f}".format(times.mean(), times.std())) 

  Intervalle programmé de direction d'itinéraire
 C nord 10,0 7,8 +/- 12,5
                       12,0 7,4 +/- 5,7
                       15,0 8,8 +/- 6,4
          sud 10,0 6,2 +/- 6,3
                       12,0 6,8 +/- 5,2
                       15,0 8,4 +/- 7,3
 D nord 10,0 6,1 +/- 7,1
                       12,0 6,5 +/- 4,6
                       15,0 7,9 +/- 5,3
          sud 10,0 6,7 +/- 5,3
                       12,0 7,5 +/- 5,9
                       15,0 8,8 +/- 6,5
 E nord 10,0 5,5 +/- 3,7
                       12,0 6,5 +/- 4,3
                       15,0 7,9 +/- 4,9
          sud 10,0 6,8 +/- 5,6
                       12,0 7,3 +/- 5,2
                       15,0 8,7 +/- 6,0
 Nom: réel, dtype: objet 

Le temps d'attente moyen, peut-être une minute ou deux, représente plus de la moitié de l'intervalle prévu, mais n'est pas égal à l'intervalle prévu, comme l'indique le paradoxe du temps d'attente. En d'autres termes, le paradoxe d'inspection est confirmé, mais le paradoxe du temps d'attente n'est pas vrai.

Conclusion

Le paradoxe de la latence était un point de départ intéressant pour une discussion qui comprenait la modélisation, la théorie des probabilités et la comparaison des hypothèses statistiques avec la réalité. Bien que nous ayons confirmé que dans le monde réel, les lignes de bus obéissent à une sorte de paradoxe d'inspection, l'analyse ci-dessus montre de manière assez convaincante: l'hypothèse principale sous-jacente au paradoxe du temps d'attente - que l'arrivée des bus suit les statistiques du processus de Poisson - n'est pas justifiée.

Rétrospectivement, cela n'est pas surprenant: le processus de Poisson est un processus sans mémoire, qui suppose que la probabilité d'arrivée est complètement indépendante du temps par rapport au moment de l'arrivée précédente. En effet, un système de transports publics bien géré a des horaires spécialement structurés pour éviter ce comportement: les bus ne démarrent pas leurs itinéraires à des moments aléatoires de la journée, mais démarrent selon l'horaire choisi pour le transport le plus efficace des passagers.

La leçon la plus importante est de faire attention aux hypothèses que vous faites sur toute tâche d'analyse de données. Parfois, le processus de Poisson est une bonne description des données d'heure d'arrivée. Mais ce n'est pas parce qu'un type de données ressemble à un autre type de données que les hypothèses admises pour l'un sont nécessairement valables pour l'autre. Souvent, des hypothèses qui semblent correctes peuvent conduire à des conclusions qui ne sont pas vraies.