Il y a un an et demi, j'ai publié l'article
«Mathématiques sur les doigts: méthodes des moindres carrés» , qui a reçu une réponse très décente, qui, entre autres, consistait dans le fait que j'ai proposé de dessiner un hibou. Eh bien, depuis un hibou, alors vous devez l'expliquer à nouveau. Dans une semaine, sur ce sujet exactement, je commencerai à donner plusieurs conférences aux étudiants en géologie; J'en profite, je présente ici les principaux points (adaptés) sous forme de projet. Mon objectif principal n'est pas de donner une recette prête à l'emploi à partir d'un livre sur les aliments savoureux et sains, mais d'expliquer pourquoi il en est ainsi et quoi d'autre est dans la section correspondante, parce que les liens entre les différentes sections de mathématiques sont les plus intéressants!
Pour le moment, j'ai l'intention de casser le texte comme suit:
Je vais aller aux moindres carrés un peu sur le côté, à travers le principe du maximum de vraisemblance, et cela nécessite une orientation minimale dans la théorie des probabilités. Ce texte est conçu pour la troisième année de notre faculté de géologie, ce qui signifie (du point de vue de l'équipement impliqué!) Qu'un lycéen intéressé avec le zèle approprié devrait pouvoir le comprendre.
À quel point le théoricien est-il solide ou croyez-vous à la théorie de l'évolution?
Un jour, on m'a demandé si je croyais en la théorie de l'évolution. Faites une pause maintenant, réfléchissez à la façon dont vous y répondrez.

Personnellement, j'ai été surpris, j'ai répondu que je trouvais cela crédible et que la question de la foi ne se posait pas du tout ici. La théorie scientifique a peu à voir avec la foi. Bref, la théorie ne fait que construire un modèle du monde qui nous entoure, il n'y a pas besoin d'y croire. De plus,
le critère de Popper nécessite une théorie scientifique pour pouvoir réfuter. Et une théorie solide devrait également posséder, tout d'abord, un pouvoir prédictif. Par exemple, si vous modifiez génétiquement des cultures de manière à ce qu'elles produisent elles-mêmes des pesticides, il est logique que des insectes résistants apparaissent. Cependant, il est nettement moins évident que ce processus peut être ralenti en faisant pousser des plantes ordinaires côte à côte avec des plantes génétiquement modifiées. Sur la base de la théorie de l'évolution, la simulation correspondante a fait
une telle prédiction , et cela semble être
confirmé .
Et qu'est-ce que les moindres carrés ont à voir avec ça?
Comme je l'ai mentionné plus tôt, je vais passer aux moindres carrés selon le principe du maximum de vraisemblance. Illustrons avec un exemple. Supposons que nous soyons intéressés par les données sur la croissance des pingouins, mais nous ne pouvons mesurer que quelques-uns de ces beaux oiseaux. Il est tout à fait logique d'introduire un modèle de distribution de croissance dans la tâche - le plus souvent c'est normal. La distribution normale est caractérisée par deux paramètres - la valeur moyenne et l'écart type. Pour chaque valeur fixe des paramètres, nous pouvons calculer la probabilité de générer exactement les mesures que nous avons effectuées. De plus, en variant les paramètres, nous trouvons ceux qui maximisent la probabilité.
Ainsi, pour travailler avec un maximum de vraisemblance, nous devons opérer en termes de théorie des probabilités. Un peu plus bas, sur les doigts, nous définissons le concept de probabilité et de vraisemblance, mais je voudrais d'abord me concentrer sur un autre aspect. Étonnamment, je vois rarement des gens penser au mot «théorie» dans l'expression «théorie des probabilités».
Qu'est-ce que le théoricien de l'apprentissage?
En ce qui concerne les origines, les significations et la portée des estimations de probabilité, un débat violent dure depuis plus de cent ans. Par exemple,
Bruno De Finetti a déclaré que la probabilité n'est rien de plus qu'une analyse subjective de la probabilité que quelque chose se produise et que cette probabilité n'existe pas en dehors de l'esprit. C'est la volonté d'une personne de parier sur quelque chose qui se passe. Cette opinion est directement opposée à l'opinion des
classiques / freventistes sur la probabilité d'un résultat spécifique d'un événement, dans laquelle on suppose que le même événement peut être répété plusieurs fois, et la "probabilité" d'un résultat particulier est liée à la fréquence d'un résultat spécifique tombant lors de tests répétés. En plus des subjectivistes et des freventistes, il y a aussi des objectivistes qui soutiennent que les probabilités sont des aspects réels de l'univers, et pas seulement des descriptions du degré de confiance de l'observateur.
Quoi qu'il en soit, mais les trois écoles scientifiques utilisent en pratique le même appareil basé sur les axiomes de Kolmogorov. Donnons un argument indirect, d'un point de vue subjectiviste, en faveur de la théorie des probabilités, construite sur les axiomes de Kolmogorov. Nous donnons les axiomes eux-mêmes un peu plus tard, mais pour commencer, nous supposerons que nous avons un bookmaker qui acceptera les paris sur la prochaine Coupe du monde. Ayons deux événements: a = l'équipe d'Uruguay deviendra champion, b = l'équipe allemande deviendra champion. Le bookmaker estime les chances de l'équipe uruguayenne de gagner à 40%, les chances de l'équipe allemande à 30%. Évidemment, l'Allemagne et l'Uruguay ne peuvent pas gagner en même temps, donc la chance de a∧b est nulle. Eh bien, en même temps, le bookmaker estime que la probabilité que l'Uruguay ou l'Allemagne (et non l'Argentine ou l'Australie) gagne est de 80%. Écrivons-le sous la forme suivante:

Si le bookmaker prétend que son degré de confiance dans l'événement
a est de 0,4, c'est-à-dire
P (a) = 0,4, alors le joueur peut choisir s'il pariera pour ou contre le fait de dire
a , des montants de paris compatibles avec le degré de confiance du bookmaker. Cela signifie que le joueur peut parier que l'événement se produira en misant quatre roubles contre six roubles du bookmaker. Ou un joueur peut parier six roubles au lieu de quatre roubles d'un bookmaker que l'événement ne se produira pas.
Si le degré de confiance du bookmaker ne reflète pas exactement l'état du monde, alors nous pouvons compter sur le fait qu'à long terme, il perdra de l'argent pour les joueurs dont les croyances sont plus précises. De plus, dans cet exemple particulier, le joueur a une stratégie dans laquelle le bookmaker perd
toujours de l' argent. Illustrons-le:

Le joueur fait trois paris, et quel que soit le résultat du championnat, il gagne toujours. Veuillez noter que la prise en compte des gains n'inclut pas en principe si l'Uruguay ou l'Allemagne sont les favoris du championnat, la perte du bookmaker est garantie! Cette situation était due au fait que le bookmaker n'était pas guidé par les bases de la théorie des probabilités, ayant violé le troisième axiome de Kolmogorov, apportons-les tous les trois:
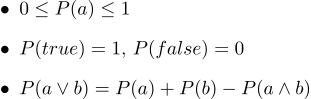
Sous forme de texte, ils ressemblent à ceci:
- 1. Toutes les probabilités vont de 0 à 1
- 2. Bien sûr, les vrais énoncés ont une probabilité de 1 et certainement une fausse probabilité de 0.
- 3. Le troisième axiome est l'axiome de la disjonction, il est facile à comprendre intuitivement, notant que les cas où la déclaration a est vraie, ainsi que les cas où b est vrai, couvrent certainement tous les cas où la déclaration a∨b est vraie; mais dans la somme de deux ensembles de cas, leur intersection se produit deux fois, il est donc nécessaire de soustraire P (a∧b).
En 1931, de Finetti
s'est avéré une déclaration très forte:
Si le bookmaker est guidé par de nombreux degrés de confiance, ce qui viole les axiomes de la théorie des probabilités, il existe une telle combinaison de paris sur les joueurs qui garantit la perte du bookmaker (le joueur gagne) à chaque pari.
Les axiomes des probabilités peuvent être considérés comme limitant l'ensemble des croyances probabilistes qu'un agent peut détenir. Veuillez noter que suivre le bookmaker n'implique pas les axiomes de Kolmogorov qu'il gagnera (nous laisserons de côté les problèmes de commission), mais si vous ne les suivez pas, il sera assuré de perdre. Il est à noter que d'autres arguments ont été avancés en faveur de l'application des probabilités; mais c'est le succès
pratique des systèmes de raisonnement basés sur la théorie des probabilités qui s'est avéré être une incitation attrayante qui a provoqué une révision de nombreux points de vue.
Nous avons donc légèrement ouvert le voile sur la
raison pour laquelle le théoricien peut avoir un sens, mais quel type d'objets manipule-t-il? La théorie entière est construite sur seulement trois axiomes; les trois impliquent une fonction magique
P. De plus, en regardant ces axiomes, cela me rappelle beaucoup la fonction de la zone de forme. Essayons de voir si la zone fonctionne pour déterminer la probabilité.
Nous définissons le mot «événement» comme «un sous-ensemble d'un carré unitaire». Nous définissons le mot «probabilité d'un événement» comme «l'aire du sous-ensemble correspondant». En gros, nous avons une grande cible en carton, et nous, ayant fermé les yeux, tirons dessus. Les chances qu'une balle tombe dans un ensemble donné sont directement proportionnelles à la zone de l'ensemble. Un événement fiable dans ce cas est le carré entier, et évidemment faux, par exemple, n'importe quel point du carré. Il résulte de notre définition de la probabilité qu'il est impossible d'arriver au point parfaitement (notre balle est un point matériel). J'aime beaucoup les images, j'en dessine beaucoup, et théoricien ne fait pas exception! Illustrons les trois axiomes:
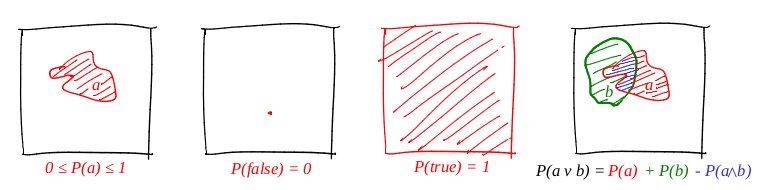
Ainsi, le premier axiome est rempli: la zone n'est pas négative et ne peut pas dépasser les unités. Un événement fiable est le carré entier, et un événement délibérément faux est n'importe quel ensemble de zone zéro. Et cela fonctionne parfaitement avec le disjoint!
Crédibilité maximale avec des exemples
Exemple un: Coin Flip
Regardons l'exemple le plus simple d'un tirage au sort, alias
le schéma de Bernoulli .
N expériences sont effectuées, dans chacune desquelles un événement sur deux peut se produire («succès» ou «échec»), l'un avec la probabilité
p , et le second avec la probabilité
1-p . Notre tâche est de trouver la probabilité d'obtenir exactement
k succès dans ces
n expériences. Cette probabilité nous donne la formule de Bernoulli:
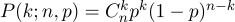
Prenez une pièce ordinaire (
p = 0,5 ), lancez-la dix fois (
n = 10 ) et considérez combien de fois les queues sont lâchées:
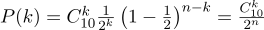
Voici un graphique de la densité de probabilité:
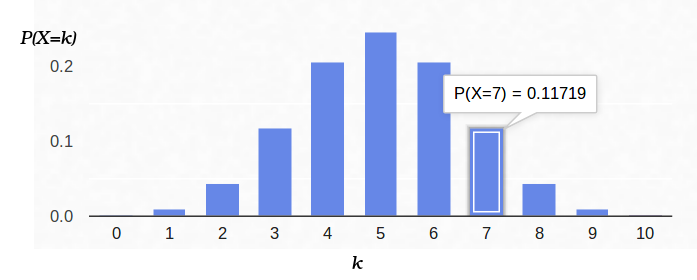
Ainsi, si nous fixons la probabilité d'apparition du «succès» (0,5) et enregistrons également le nombre d'expériences (10), le nombre possible de «succès» peut être n'importe quel entier entre 0 et 10, cependant, ces résultats ne sont pas également probables. Il est évident qu'obtenir cinq «succès» est beaucoup plus probable qu'improbable. Par exemple, la probabilité de compter sept queues est d'environ 12%.
Examinons maintenant la même tâche de l'autre côté. Nous avons une vraie pièce, mais nous ne connaissons pas sa distribution de la probabilité a priori de «succès» / «échec». Cependant, nous pouvons le lancer dix fois et compter le nombre de «succès». Par exemple, nous avons sept queues. Comment cela nous aide-t-il à évaluer
p ?
On peut essayer de fixer
n = 10 et
k = 7 dans la formule de Bernoulli, en laissant
p un paramètre libre:

La formule de Bernoulli peut alors être interprétée comme la
vraisemblance du paramètre estimé (dans ce cas,
p ). J'ai même changé la lettre de la fonction, maintenant c'est
L (de l'anglais likehood). Autrement dit, la probabilité est la probabilité de générer des données d'observation (7 queues de 10 expériences) pour une valeur donnée du ou des paramètres.
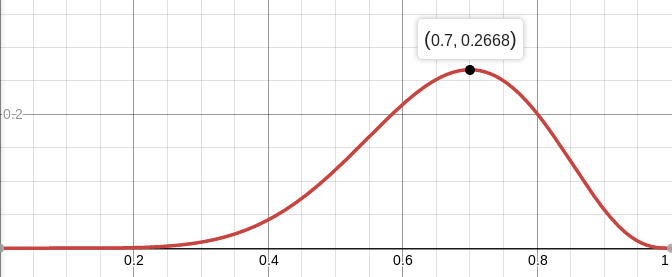
Par exemple, la probabilité d'une pièce équilibrée (
p = 0,5), à condition que sept queues sur dix se produisent, est d'environ 12%. Vous pouvez tracer la fonction
L :
Donc, nous recherchons une valeur de paramètres qui maximise la probabilité d'obtenir ces observations que nous avons. Dans ce cas particulier, nous avons une fonction d'une variable, nous recherchons son maximum. Afin de faciliter la recherche, je chercherai un maximum non pas
L , mais
log L. Le logarithme est une fonction strictement monotone, donc maximiser l'un et l'autre est exactement la même chose. Et le logarithme divise le produit en une quantité beaucoup plus pratique à différencier. Nous recherchons donc le maximum de cette fonction:

Pour ce faire, nous assimilons sa dérivée à zéro:
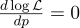
La dérivée de log x = 1 / x, on obtient:

Autrement dit, la probabilité maximale (environ 27%) est atteinte à

Juste au cas où, nous calculons la dérivée seconde:
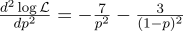
Au point p = 0,7, il est négatif, donc ce point est vraiment le maximum de la fonction L.
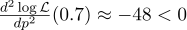
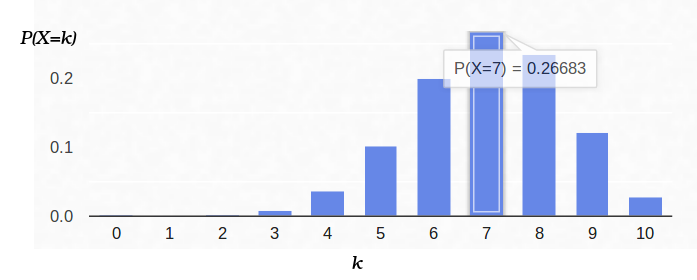
Et voici la densité de probabilité pour le schéma de Bernoulli avec
p = 0,7:
Exemple deux: ADC
Imaginons que nous ayons une certaine quantité physique constante que nous voulons mesurer, que ce soit une longueur avec une règle ou une tension avec un voltmètre. Toute mesure donne une
approximation de cette quantité, mais pas la quantité elle-même. Les méthodes que je décris ici ont été développées par Gauss à la fin du XVIIIe siècle, lorsqu'il a mesuré les orbites des corps célestes.
Par exemple, si nous mesurons N fois la tension de la batterie, nous obtenons N mesures différentes. Lequel prendre? C’est tout! Alors, ayons N quantités Uj:
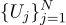
Supposons que chaque mesure Uj soit égale à une valeur idéale, plus un bruit gaussien, qui est caractérisé par deux paramètres - la position de la cloche gaussienne et sa «largeur». Voici la densité de probabilité:
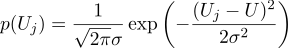
Autrement dit, ayant N valeurs Uj données, notre tâche consiste à trouver un tel paramètre, U qui maximise la valeur de vraisemblance. La crédibilité (j'en retire immédiatement le logarithme) peut s'écrire comme suit:
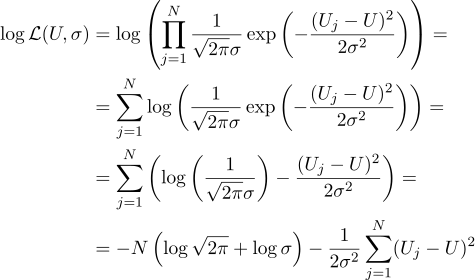
Eh bien, alors tout est strictement comme avant, nous égalons à zéro dérivées partielles par rapport aux paramètres que nous recherchons:
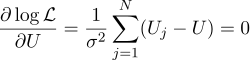
Nous constatons que l'estimation la plus probable de la quantité inconnue U peut être trouvée comme la moyenne de toutes les mesures:
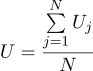
Eh bien, le paramètre sigma le plus probable est l'écart-type habituel:
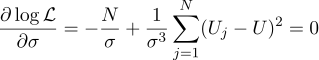

Cela valait-il la peine d'obtenir une moyenne simple de toutes les mesures dans la réponse? À mon goût, ça valait le coup. Soit dit en passant, la moyenne de plusieurs mesures d'une valeur constante afin d'augmenter la précision des mesures est une pratique standard. Par exemple,
moyenne ADC . Au fait, pour que ce bruit gaussien ne soit pas nécessaire, il suffit que le bruit soit non biaisé.
Exemple trois, et encore unidimensionnel
Nous continuons la conversation, prenons le même exemple, mais compliquons un peu. Nous voulons mesurer la résistance d'une certaine résistance. Avec l'aide d'une alimentation électrique de laboratoire, nous pouvons passer un certain nombre standard d'ampères à travers elle et mesurer la tension qui est nécessaire pour cela. Autrement dit, nous aurons N paires de nombres (Ij, Uj) à l'entrée de notre évaluateur de résistance.
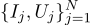
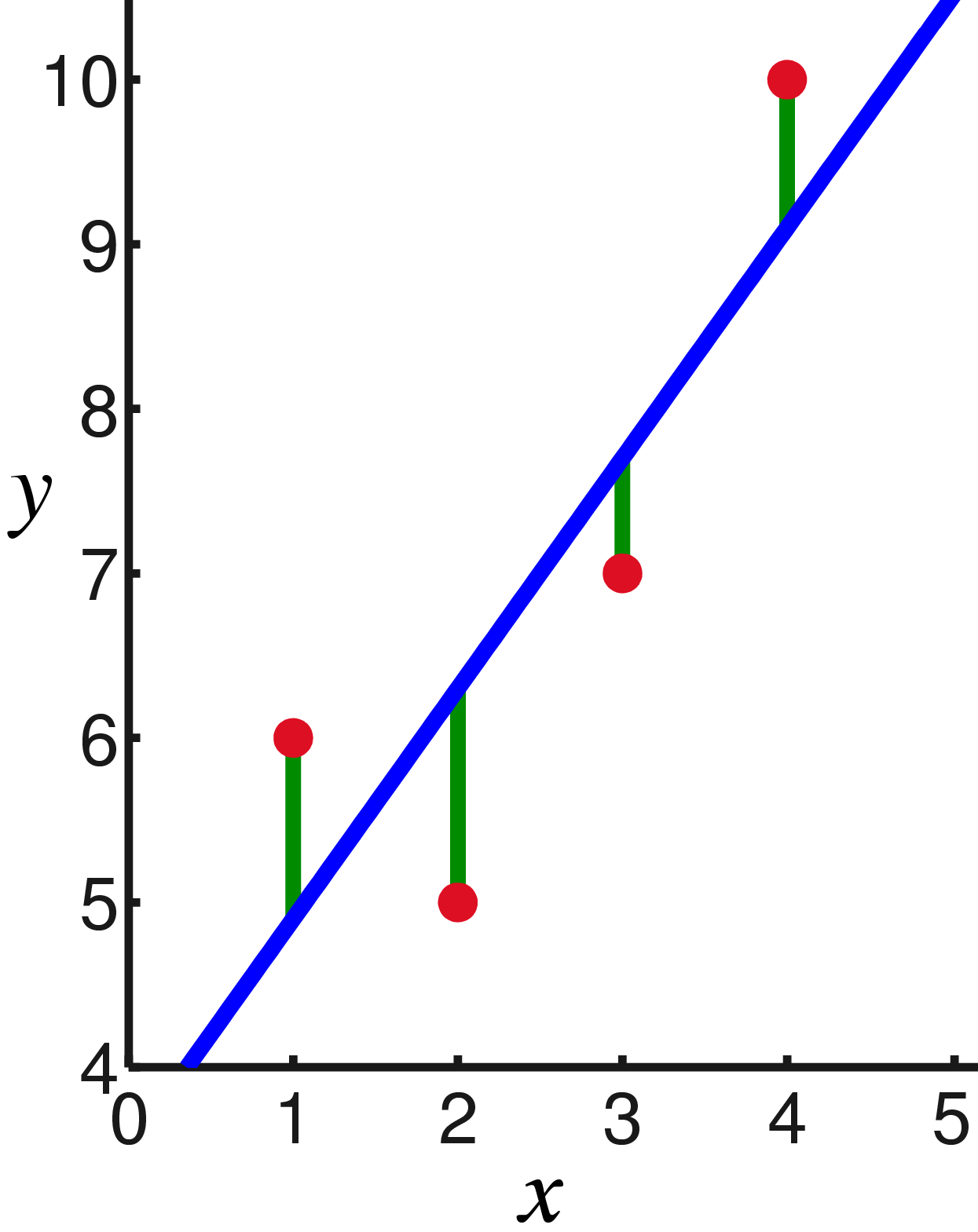
Dessinez ces points sur le graphique; La loi d'Ohm nous dit que nous recherchons la pente de la ligne bleue.
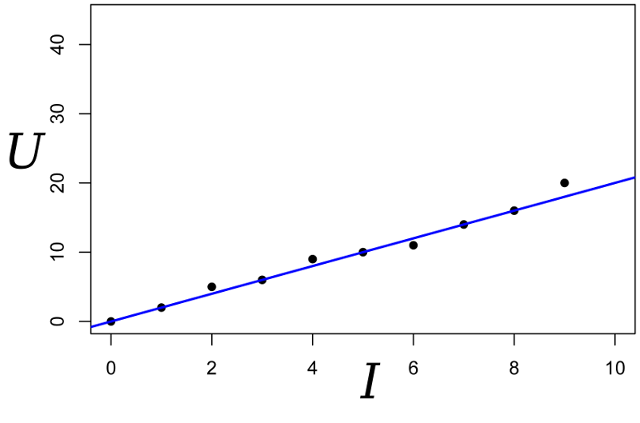
Nous écrivons l'expression de la vraisemblance du paramètre R:
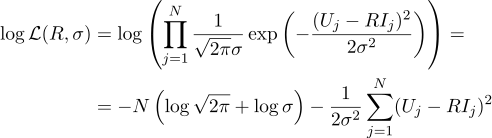
Et encore une fois, nous égalons à zéro la dérivée partielle correspondante:
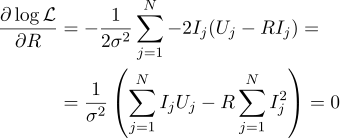
La résistance R la plus plausible peut alors être trouvée par la formule suivante:
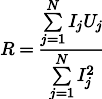
Ce résultat est déjà un peu moins évident que la moyenne simple de toutes les mesures. Veuillez noter que si nous prenons cent mesures dans la région d'un ampère et une mesure dans la région d'un kilo ampère, alors les cent mesures précédentes n'affecteront pratiquement pas le résultat. Rappelons-nous ce fait, il nous sera utile dans le prochain article.
Quatrième exemple: retour aux moindres carrés
Vous avez sûrement déjà remarqué que dans les deux derniers exemples, maximiser le logarithme de vraisemblance équivaut à minimiser la somme des carrés de l'erreur d'estimation. Regardons un autre exemple. Prenez l'étalonnage du steelyard en utilisant des poids de référence. Supposons que nous ayons N charges de référence de masse xj, accrochons-les à un steelyard et mesurons la longueur du ressort, nous obtenons N longueurs de ressort yj:

La loi de Hooke nous dit que l'extension du ressort dépend linéairement de la force appliquée, et cette force comprend le poids des marchandises et le poids du ressort lui-même. Soit la rigidité du ressort le paramètre
a , mais la tension du ressort sous son propre poids est le paramètre b. On peut alors écrire l'expression de la vraisemblance de nos mesures de cette manière (comme précédemment, sous l'hypothèse du bruit de mesure gaussien):
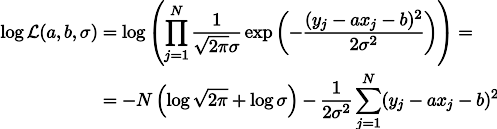
La maximisation de vraisemblance de L équivaut à minimiser la somme des carrés des erreurs d'estimation, c'est-à-dire que nous pouvons rechercher le minimum de la fonction S définie comme suit:
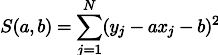
En d'autres termes, nous recherchons une ligne droite qui minimise la somme des carrés des longueurs des segments verts:
Eh bien, pas de surprise, nous mettons à zéro les dérivées partielles:
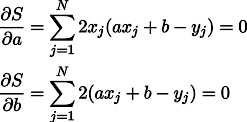
Nous obtenons un système de deux équations linéaires avec deux inconnues:
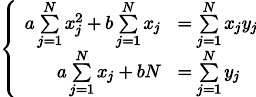
Nous rappelons la septième année de l'école et écrivons la solution:

Conclusion
Les méthodes des moindres carrés sont un cas particulier de maximisation de la vraisemblance dans les cas où la densité de probabilité est gaussienne. Dans le cas où la densité est (pas du tout) gaussienne, les moindres carrés donnent une estimation différente de la MLE (estimation de similitude maximale). Soit dit en passant, à un moment donné, Gauss a émis l'hypothèse que la distribution ne joue aucun rôle, seule l'indépendance des tests est importante.
Comme vous pouvez le voir dans cet article, plus la forêt est éloignée, plus les solutions analytiques à ce problème sont lourdes. Eh bien, oui nous ne sommes pas au XVIIIe siècle, nous avons des ordinateurs! La prochaine fois, nous verrons une approche géométrique et, ensuite, programmatique du problème de l'OLS, restons sur la ligne.