J'ai préparé longtemps et collecté du matériel, j'espère que cette fois, ça s'est mieux passé. Je consacre cet article aux méthodes de base pour résoudre les problèmes d'optimisation mathématique avec des limitations, donc si vous avez entendu que la méthode simplex est une méthode
très importante , mais que vous ne savez toujours pas ce qu'elle fait, cet article vous aidera probablement.
PS L'article contient des formules mathématiques ajoutées par l'éditeur de macro. Ils disent que parfois ils ne sont pas affichés. Il existe également de nombreuses animations au format gif.
Préambule
Le problème de l'optimisation mathématique est un problème de la forme «Rechercher dans l'ensemble
mathcalK l'élément
x∗ de telle sorte que pour tous
x de
mathcalK exécuté
f(x∗) leqf(x) ", Qui dans la littérature scientifique est susceptible d'être écrit quelque chose comme ça
\ begin {array} {rl} \ mbox {minimiser} & f (x) \\ \ mbox {fourni} & x \ in \ mathcal {K}. \ end {array}
\ begin {array} {rl} \ mbox {minimiser} & f (x) \\ \ mbox {fourni} & x \ in \ mathcal {K}. \ end {array}
Historiquement, les méthodes populaires telles que la descente en gradient ou la méthode de Newton ne fonctionnent que dans des espaces linéaires (et de préférence simples, par exemple
mathbbRn ) Dans la pratique, il y a souvent des problèmes où vous devez trouver un minimum non dans un espace linéaire. Par exemple, vous devez trouver le minimum d'une fonction sur de tels vecteurs
x=(x1, ldots,xn) pour lequel
xi geq0 , cela peut être dû au fait que
xi dénoter les longueurs de tous les objets. Ou par exemple, si
x représentent les coordonnées d'un point qui ne doit pas dépasser
r de
y c'est-à-dire
|x−y | leqr . Pour de tels problèmes, la descente de gradient ou la méthode de Newton n'est plus directement applicable. Il s'est avéré qu'une très grande classe de problèmes d'optimisation est commodément couverte par des «restrictions», similaires à celles que j'ai décrites ci-dessus. En d'autres termes, il est commode de représenter l'ensemble
mathcalK sous la forme d'un système d'égalités et d'inégalités
beginarraylgi(x) leq0, 1 leqi leqm,hi(x)=0, 1 leqi leqk. endarray
Problèmes de minimisation sur un espace du formulaire
mathbbRn ils ont donc commencé à les appeler arbitrairement «problème sans contrainte» et problèmes sur des ensembles définis par des ensembles d'égalités et d'inégalités - «problèmes contraints».
Techniquement, absolument n'importe quelle multitude
mathcalK peut être représenté comme une égalité ou une inégalité unique à l'aide de la fonction d'
indicateur , qui est définie comme
I_ \ mathcal {K} (x) = \ begin {cases} 0, & x \ notin \ mathcal {K} \\ 1, & x \ in \ mathcal {K}, \ end {cases}
I_ \ mathcal {K} (x) = \ begin {cases} 0, & x \ notin \ mathcal {K} \\ 1, & x \ in \ mathcal {K}, \ end {cases}
cependant, une telle fonction n'a pas diverses propriétés utiles (convexité, différentiabilité, etc.). Cependant, on peut souvent imaginer
mathcalK sous la forme de plusieurs égalités et inégalités, chacune ayant de telles propriétés. La théorie de base est résumée sous le cas
\ begin {array} {rl} \ mbox {minimiser} & f (x) \\ \ mbox {fourni} & g_i (x) \ leq 0, ~ 1 \ leq i \ leq m \\ & Ax = b , \ end {array}
\ begin {array} {rl} \ mbox {minimiser} & f (x) \\ \ mbox {fourni} & g_i (x) \ leq 0, ~ 1 \ leq i \ leq m \\ & Ax = b , \ end {array}
où
f,gi - fonctions convexes (mais pas nécessairement différenciables),
A - matrice. Pour démontrer le fonctionnement des méthodes, j'utiliserai deux exemples:
- Tâche de programmation linéaire
$$ afficher $$ \ begin {array} {rl} \ mbox {minimiser} & -2 & x ~~~ - & y \\ \ mbox {fourni} & -1.0 & ~ x -0.1 & ~ y \ leq -1.0 \ \ & -1,0 & ~ x + ~ 0,6 & ~ y \ leq -1,0 \\ & -0,2 & ~ x + ~ 1,5 & ~ y \ leq -0,2 \\ & ~ 0,7 & ~ x + ~ 0,7 & ~ y \ leq 0.7 \\ & ~ 2.0 & ~ x -0.2 & ~ y \ leq 2.0 \\ & ~ 0.5 & ~ x -1.0 & ~ y \ leq 0.5 \\ & -1.0 & ~ x -1.5 & ~ y \ leq - 1.0 \\ \ end {array} $$ display $$
En substance, ce problème consiste à trouver le point le plus éloigné du polygone dans la direction (2, 1), la solution au problème est le point (4.7, 3.5) - le plus «droit» du polygone). Mais le polygone lui-même

- Minimisation d'une fonction quadratique avec une contrainte quadratique
\ begin {array} {rl} \ mbox {minimiser} & 0,7 (x - y) ^ 2 + 0,1 (x + y) ^ 2 \\ \ mbox {fourni} & (x-4) ^ 2 + ( y-6) ^ 2 \ leq 9 \ end {array}
\ begin {array} {rl} \ mbox {minimiser} & 0,7 (x - y) ^ 2 + 0,1 (x + y) ^ 2 \\ \ mbox {fourni} & (x-4) ^ 2 + ( y-6) ^ 2 \ leq 9 \ end {array}
Méthode simplex
De toutes les méthodes que je couvre avec cette revue, la méthode simplex est probablement la plus célèbre. La méthode a été développée spécifiquement pour la programmation linéaire et la seule parmi celles présentées présente la solution exacte en un nombre fini d'étapes (à condition que l'arithmétique exacte soit utilisée pour les calculs, en pratique, ce n'est généralement pas le cas, mais en théorie, c'est possible). L'idée d'une méthode simplex se compose de deux parties:
- Des systèmes d'inégalités et d'égalités linéaires définissent des polyèdres convexes multidimensionnels (polytopes). Dans le cas unidimensionnel, c'est un point, un rayon ou un segment; dans le cas bidimensionnel, c'est un polygone convexe; dans le cas tridimensionnel, c'est un polyèdre convexe. Minimiser la fonction linéaire, c'est essentiellement trouver le point «le plus éloigné» dans une certaine direction. Je pense que l'intuition devrait suggérer que ce point le plus éloigné devrait être un certain pic, et c'est effectivement le cas. En général, pour un système de m inégalités dans n -espace dimensionnel un sommet est un point satisfaisant un système pour lequel exactement n de ces inégalités se transforment en égalités (à condition qu'il n'y ait pas d'équivalents parmi les inégalités). Il y a toujours un nombre fini de tels points, bien qu'il puisse y en avoir beaucoup.
- Nous avons maintenant un ensemble fini de points, d'une manière générale, vous pouvez simplement les sélectionner et les trier, c'est-à-dire faire quelque chose comme ceci: pour chaque sous-ensemble de n inégalités, résoudre le système d'équations linéaires compilé sur les inégalités choisies, vérifier que la solution correspond au système d'origine des inégalités et comparer avec d'autres points de ce type. Il s'agit d'une méthode assez simple mais inefficace mais qui fonctionne. La méthode simplex, au lieu d'itérer, se déplace de haut en haut le long des bords afin que les valeurs de la fonction objectif s'améliorent. Il s'avère que si un sommet n'a pas de «voisins» dans lesquels les valeurs de la fonction sont meilleures, alors c'est optimal.
La méthode simplex est itérative, c'est-à-dire qu'elle améliore séquentiellement légèrement la solution. Pour de telles méthodes, vous devez commencer quelque part, dans le cas général cela se fait en résolvant un problème auxiliaire
\ begin {array} {rl} \ mbox {minimiser} & s \\ \ mbox {fourni} & g_i (x) \ leq s, ~ 1 \ leq i \ leq m \\ \ end {array}
\ begin {array} {rl} \ mbox {minimiser} & s \\ \ mbox {fourni} & g_i (x) \ leq s, ~ 1 \ leq i \ leq m \\ \ end {array}
Si pour résoudre ce problème
x∗,s∗ tel que
s∗ leq0 puis exécuté
gi(x∗) leqs leq0 sinon, le problème d'origine est généralement donné sur un ensemble vide. Pour résoudre le problème auxiliaire, vous pouvez également utiliser la méthode simplex, mais le point de départ peut être pris
s= maxigi(x) avec arbitraire
x . Trouver le point de départ peut être arbitrairement appelé la première phase de la méthode, trouver la solution au problème d'origine peut être arbitrairement appelé la deuxième phase de la méthode.
La trajectoire de la méthode du simplexe diphasiqueLa trajectoire a été générée à l'aide de scipy.optimize.linprog.
Descente de gradient projectif
À propos de la descente de gradient, j'ai récemment écrit un
article séparé dans lequel j'ai également brièvement décrit cette méthode. Maintenant, cette méthode est assez vivante, mais est étudiée dans le cadre d'une
descente de gradient proximal plus générale. L'idée même de la méthode est assez banale: si l'on applique la descente de gradient à une fonction convexe
f puis avec le bon choix de paramètres on obtient un minimum global
f . Si, après chaque étape de la descente de gradient, le point obtenu est corrigé, en prenant plutôt sa projection sur un ensemble convexe fermé
mathcalK , puis en conséquence, nous obtenons le minimum de la fonction
f sur
mathcalK . Eh bien, ou plus formellement, la descente du gradient projectif est un algorithme qui calcule séquentiellement
begincasesxk+1=yk− alphak nablaf(yk)yk+1=P mathcalK(xk+1), fincas
où
P mathcalK(x)= mboxargminy in mathcalK |x−y |.
La dernière égalité définit l'opérateur standard de projection sur l'ensemble, en fait c'est une fonction qui, selon le point
x calcule le point le plus proche de l'ensemble
mathcalK . Le rôle de la distance joue ici
| ldots | , il convient de noter que n'importe quelle
norme peut être utilisée ici, cependant, les projections avec des normes différentes peuvent différer!
En pratique, la descente par gradient projectif n'est utilisée que dans des cas particuliers. Son principal problème est que le calcul de la projection peut être encore plus difficile que l'original et doit être calculé plusieurs fois. Le cas le plus courant pour lequel il est pratique d'utiliser la descente de gradient projectif est celui des «restrictions de boîte», qui ont la forme
elli leqxi leqri, 1 leqi leqn.
Dans ce cas, la projection est calculée très simplement, pour chaque coordonnée il s'avère
[P _ {\ mathcal {K}} (x)] _ i = \ begin {cases} r_i, & x_i> r_i \\ \ ell_i, & x_i <\ ell_i \\ x_i, & x_i \ in [\ ell_i, r_i ]. \ end {cases}
[P _ {\ mathcal {K}} (x)] _ i = \ begin {cases} r_i, & x_i> r_i \\ \ ell_i, & x_i <\ ell_i \\ x_i, & x_i \ in [\ ell_i, r_i ]. \ end {cases}
L'utilisation de la descente du gradient projectif pour des problèmes de programmation linéaire n'a aucun sens, cependant, si vous faites cela, cela ressemblera à ceci
Trajectoire de descente du gradient projectif pour un problème de programmation linéaire Et voici la trajectoire de la descente du gradient projectif pour le deuxième problème, si
choisissez une grande taille de pas et si
choisissez une petite taille de pas Méthode ellipsoïde
Cette méthode est remarquable en ce qu'elle est le premier algorithme polynomial pour les problèmes de programmation linéaire; elle peut être considérée comme une généralisation multidimensionnelle de
la méthode de bissection . Je vais commencer par une
méthode plus générale
de séparation de l'hyperplan :
- À chaque étape de la méthode, un ensemble contient la solution au problème.
- À chaque étape, un hyperplan est construit, après quoi tous les points se trouvant sur un côté de l'hyperplan sélectionné sont supprimés de l'ensemble, et de nouveaux points peuvent être ajoutés à cet ensemble
Pour les problèmes d'optimisation, la construction de «l'hyperplan de séparation» est basée sur l'inégalité suivante pour les fonctions convexes
f(y) geqf(x)+ nablaf(x)T(y−x).
Si correctif
x , puis pour une fonction convexe
f demi-espace
nablaf(x)T(y−x) geq0 contient uniquement des points dont la valeur n'est pas inférieure à un point
x , ce qui signifie qu'ils peuvent être coupés, car ces points ne sont pas meilleurs que celui que nous avons déjà trouvé. Pour les problèmes de restrictions, vous pouvez également vous débarrasser des points qui ne manqueront pas de violer l'une des restrictions.
La version la plus simple de la méthode de séparation des hyperplans consiste à couper simplement les demi-espaces sans ajouter de points. En conséquence, à chaque étape, nous aurons un certain polyèdre. Le problème avec cette méthode est que le nombre de faces du polyèdre est susceptible d'augmenter d'étape en étape. De plus, il peut croître de façon exponentielle.
La méthode ellipsoïde stocke en fait un ellipsoïde à chaque étape. Plus précisément, après la construction de l'hyperplan, un ellipsoïde de volume minimal est construit, qui contient l'une des parties de l'original. Ceci peut être réalisé en ajoutant de nouveaux points. Un ellipsoïde peut toujours être défini par une matrice définie positive et un vecteur (centre d'un ellipsoïde) comme suit
\ mathcal {E} (P, x) = \ {z ~ | ~ (z-x) ^ TP (z-x) \ leq 1 \}.
\ mathcal {E} (P, x) = \ {z ~ | ~ (z-x) ^ TP (z-x) \ leq 1 \}.
La construction d'un ellipsoïde minimum en volume, contenant l'intersection du demi-espace et d'un autre ellipsoïde, peut se faire à l'aide de
formules modérément lourdes . Malheureusement, dans la pratique, cette méthode était toujours aussi bonne que la méthode simplex ou la méthode du point interne.
Mais en fait, comment cela fonctionne
et pour
programmation quadratique Méthode du point intérieur
Cette méthode a une longue histoire de développement, l'une des premières conditions préalables est apparue à peu près au moment où la méthode simplex a été développée. Mais à l'époque, il n'était pas encore suffisamment efficace pour être utilisé dans la pratique. Plus tard en 1984, une
variante de la méthode a été développée spécifiquement pour la programmation linéaire, ce qui était bon à la fois en théorie et en pratique. De plus, la méthode du point interne ne se limite pas seulement à la programmation linéaire, contrairement à la méthode simplex, et c'est maintenant l'algorithme principal pour les problèmes d'optimisation convexes avec restrictions.
L'idée de base de la méthode est de remplacer les restrictions par une amende sous la forme de la
fonction dite
barrière . Fonction
F:Int mathcalK rightarrow mathbbR appelé la
fonction de barrière pour l'ensemble
mathcalK si
F(x) rightarrow+ infty mboxatx rightarrow partial mathcalK.
Ici
Int mathcalK - à l'intérieur
mathcalK ,
partial mathcalK - bordure
mathcalK . Au lieu du problème d'origine, il est proposé de résoudre le problème
mboxminimiserparx varphi(x,t)=tf(x)+F(x).
F et
varphi donné uniquement à l'intérieur
mathcalK (en fait, c'est de là que vient le nom), la propriété de la barrière garantit que
varphi au moins
x existe. De plus, plus
t plus l'impact est important
f . Dans des conditions raisonnablement raisonnables, vous pouvez y parvenir si vous visez
t à l'infini alors le minimum
varphi convergera vers la solution du problème d'origine.
Si l'ensemble
mathcalK donné comme un ensemble d'inégalités
gi(x) leq0, 1 leqi leqm alors le choix standard de la fonction barrière est la
barrière logarithmiqueF(x)=− summi=1 ln(−gi(x)).
Points minimum
x∗(t) les fonctions
varphi(x,t) pour différents
t forme une courbe, qui est généralement appelée le
chemin central , la méthode du point intérieur, pour ainsi dire, essaie de suivre ce chemin. Voici à quoi cela ressemble
Exemples de programmation linéaire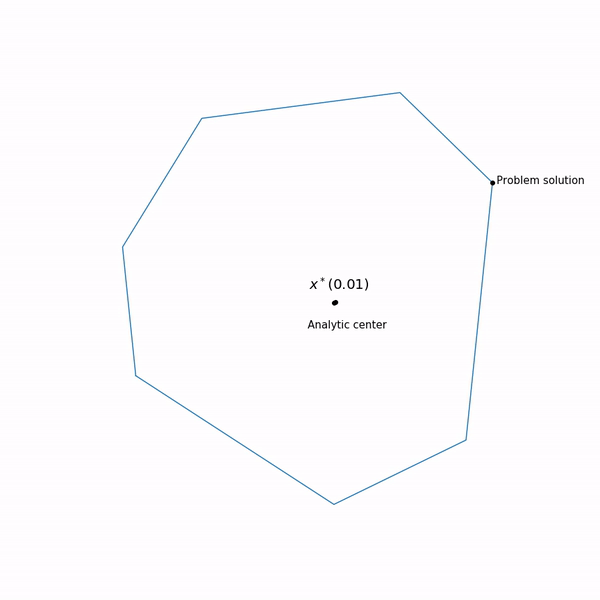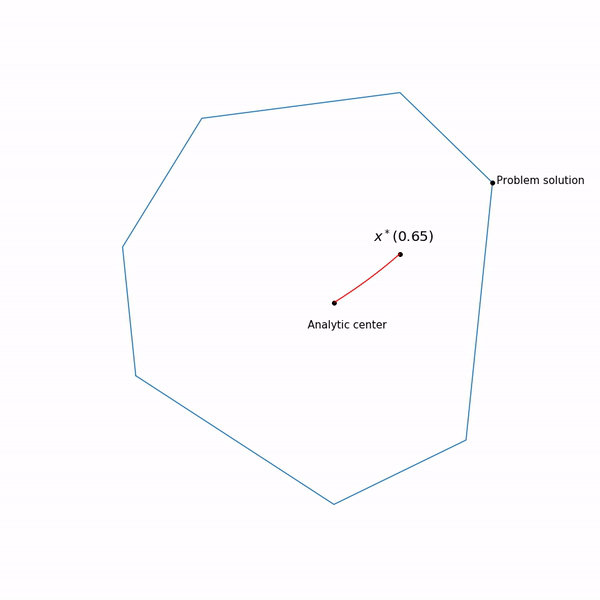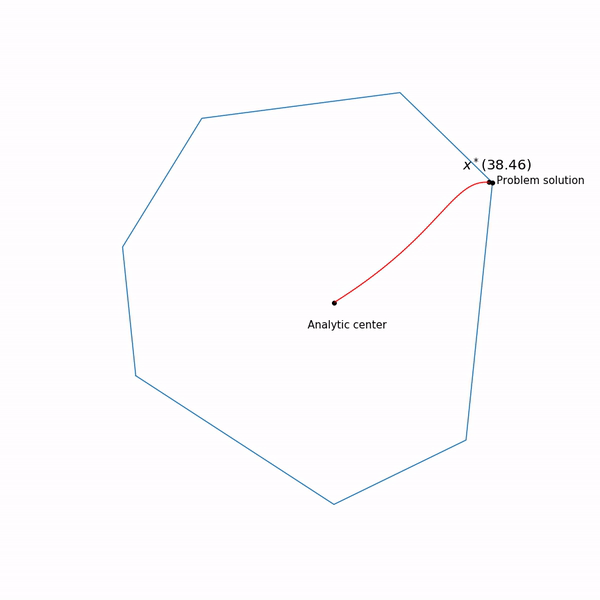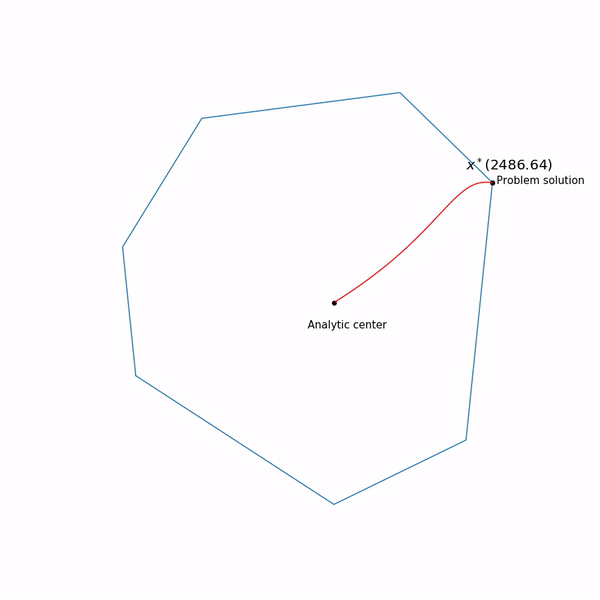 Le centre analytique
Le centre analytique est juste
x∗(0) Enfin, la méthode de point interne elle-même a la forme suivante
- Sélectionnez une approximation initiale x0 , t0>0
- Choisissez une nouvelle approximation en utilisant la méthode de Newton
xk+1=xk−[ nabla2x varphi(xk,tk)]−1 nablax varphi(xk,tk)
- Cliquer pour agrandir t
tk+1= alphatk, alpha>1
L'utilisation de la méthode Newton est ici très importante: le fait est qu'avec le bon choix de la fonction barrière, l'étape de la méthode Newton génère un point
qui reste à l'intérieur de notre ensemble , nous avons expérimenté, il ne donne pas toujours sous cette forme. Et enfin, voici à quoi ressemble la trajectoire de la méthode des points internes
Tâche de programmation linéaireLe point noir rebondissant est
x∗(tk) , c'est-à-dire point auquel nous essayons d'approcher l'étape de la méthode de Newton dans l'étape actuelle.
Problème de programmation quadratique