En 2018, nous avons organisé trois concours Yandex.Blitz: apprentissage automatique, développement mobile et front-end. Le troisième concours a eu lieu récemment - félicitations aux gagnants! En attendant, nous souhaitons revenir au second d'entre eux, où des tâches étaient proposées à la jonction d'algorithmes et de logiciels d'écriture pour Android / iOS. Les candidats au poste de développeur mobile chez Yandex bénéficieront d'une expérience dans la résolution de tels problèmes. Lisez l'analyse détaillée de certains d'entre eux. Et si vous n'avez pas participé au Blitz, il vaut mieux essayer d'abord de les résoudre vous-même .

La tâche de "l'approvisionnement en gaz"
| Entrer | Conclusion | Limite de temps | Limite de mémoire |
|---|
| entrée standard ou input.txt | sortie standard ou output.txt | 15 secondes | 15 mégaoctets |
Nika développe une application pour les cadres supérieurs d'une grande compagnie gazière pour les aider à planifier la production.
La société envisage de n champs qui sont d 1 ... d i ... d n kilomètres de la canalisation et peut produire v 1 ... v i ... v n unités de gaz. Une licence distincte est vendue pour chaque domaine - les licences sont s 1 ... s i ... s n .
Pour connecter les champs à l'autoroute, vous devez construire des pipelines. Un entrepreneur qui peut poser différents types de tuyaux aide cette entreprise. Les tuyaux diffèrent les uns des autres par leur longueur (l 1 ... l i ... l m ) et leur prix (p 1 ... p i ... p m ). Ils peuvent être combinés les uns avec les autres à votre guise.
L'entreprise possède k pièces et souhaite obtenir le plus de gaz possible.
Quelle quantité l'entreprise pourra-t-elle produire si elle donne des commandes optimales à l'entrepreneur?
Le pipeline peut être plus long que la distance du champ au pipeline.
La première ligne contient un entier k ≤ 10 5 .
La deuxième ligne contient un entier n ≤ 15.
Les n lignes suivantes contiennent trois entiers d i ≤ 100, v i ≤ 100 et s i ≤ 100.
Les nombres sont séparés par un espace.
La ligne suivante contient un entier m ≤ 15.
Les m lignes suivantes contiennent deux entiers l i ≤ 100 et p i ≤ 100. Les nombres sont séparés par un espace.
La seule ligne avec la réponse.
Des exemples
| Entrer | Conclusion |
116
3
58 7 50
81 71 56
52 57 31
3
47 9
1 25
18 61 | 57 |
Analyse
Pour commencer, définissons la notation. Soit une classe d'objets Dépôt (dépôt) avec paramètres $ inline $ Dd_ {i} $ inline $ (éloignement) $ inline $ Dv_ {i} $ inline $ (volume de production) et $ inline $ Ds_ {i} $ inline $ (coût de la licence). Les objets d'index de ce type seront la variable i. Il existe également une classe d'objets Pipeliner avec des paramètres $ inline $ PPl_ {j} $ inline $ (la longueur du tuyau que l'entrepreneur peut construire) et $ inline $ PPp_ {j} $ inline $ (prix de cette pipe), index par j. Les participants au blitz ont demandé à plusieurs reprises si un type de tuyau peut être utilisé deux fois. On suppose que non, et cet exemple montre clairement. Donc, selon les termes de cette tâche, accepter $ inline $ D_ {i} = {0, 1} $ inline $ (choisissez un champ ou non) et $ inline $ PP_ {j} = {0, 1} $ inline $ (choisissez un entrepreneur ou non), vous pouvez faire une tâche de programmation linéaire:
$ inline $ \ sum \ limits_ {i} D_ {i} * Dv_ {i} \ rightarrow max \\ \ sum \ limits_ {i} D_ {i} * Ds_ {i} + \ sum \ limits_ {j} PP_ { j} * PPp_ {j} \ leq k \\ \ sum \ limits_ {i} D_ {i} * Dd_ {i} \ leq \ sum \ limits_ {j} PP_ {j} * PPl_ {j} \\ D_ { i} = {0, 1}, PP_ {j} = {0, 1} $ inline $
Il peut être résolu, par exemple, par la méthode simplex. Cependant, selon les termes de la tâche, nous sommes tenus de renvoyer uniquement le volume de production maximal (c'est-à-dire la valeur de la fonction objectif) et il n'est pas nécessaire d'indiquer quels champs et quels entrepreneurs doivent être sélectionnés. Avec les restrictions de la condition, le problème peut être résolu par la méthode de programmation dynamique en construisant une table dp [longueur] [argent], où longueur est la longueur du pipeline, l'argent est de l'argent. Après la construction correcte de la table, il suffit d'y trouver la valeur maximale, ce qui sera la réponse. Les contraintes de mémoire de la tâche suffisent à construire.
La tâche de "Tours et IA"
| Entrer | Conclusion | Limite de temps | Limite de mémoire |
|---|
| entrée standard ou input.txt | sortie standard ou output.txt | 1 seconde | 64 mégaoctets |
Artem développe l'intelligence artificielle en jouant à un jeu mobile compétitif. Les règles du jeu sont simples.
Avant les joueurs, il y a n tours d'une hauteur de c 1 ... c i ... c n . À son tour, le joueur peut casser l'une des tours pour obtenir plusieurs tours plus petites. Les joueurs ont peur de se perdre dans les tours, ils se sont donc mis d'accord sur une limitation: après la séparation, deux tours de même hauteur ne devraient pas être obtenues. Par exemple, une tour d'une hauteur de 7 peut être divisée en (1, 2, 4), mais pas en (1, 3, 3). La hauteur est toujours un entier.
Perd celui qui n'a pas de tours qui peuvent être détruites.
Artem a un ami très intelligent qui joue de manière optimale - c'est avec lui que l'intelligence artificielle d'Artem se bat. Pour évaluer le travail de l'IA, Artyom doit savoir si le robot devrait gagner si les deux joueurs agissent de manière optimale. Aidez-le avec ça.
L'homme marche toujours en premier. Il jouera avec des jeux AI k.
La première ligne contient un entier k <500.
Ceci est suivi de k blocs de deux lignes.
La première ligne de chaque bloc est un entier 0 <n ≤ 50.
La deuxième ligne de chaque bloc a n entiers 0 <c i ≤ 50. Les nombres sont séparés par des espaces.
k lignes, chacune contenant vrai ou faux, selon qu'une personne gagne la partie.
Des exemples
| Entrer | Conclusion |
2
1
4
2
1 1 | faux
faux |
Analyse
Le jeu de tour proposé est un jeu de fin équitable pour deux joueurs dans lequel il est impossible de tirer.
Par conséquent, la victoire d'un joueur particulier dans le jeu est déterminée par l'état du jeu et l'ordre des mouvements des deux joueurs. Pour les lecteurs qui connaissent la théorie des jeux, il est évident que l'un des jeux égaux de deux joueurs est en fait équivalent au jeu «lui», ce qui signifie aussi notre jeu.
Voici une brève description de lui-un jeu ( lien vers la source - cliquez dessus pour une revue détaillée):
Il y a plusieurs piles, chacune ayant plusieurs pierres. En un coup, le joueur peut prendre n'importe quel nombre non nul de pierres d'une même pile et les jeter. En conséquence, une perte se produit lorsqu'il n'y a plus de mouvements, c'est-à-dire tous les tas sont vides.
Ainsi, l'état du jeu «lui» est uniquement décrit par un ensemble non ordonné de nombres naturels. D'un seul coup, il est permis de réduire strictement l'un des nombres (si par conséquent le nombre devient nul, alors il est supprimé de l'ensemble).
La solution au jeu nim est de trouver la somme xor à partir de la taille des tas, et ce n'est que si cette somme est non nulle que nous pouvons clairement déclarer que nous sommes dans un état gagnant.
De plus, le théorème de Spraga-Grandi vient à notre aide, qui stipule que l'état U de tout jeu peer-to-peer de deux joueurs peut être associé à une poignée de jeux lui de taille X. Dès qu'une fonction spécifiant le mappage des états de notre jeu à lui-jeu est trouvée, la solution pour le résoudre - un jeu qui est déjà connu.
Tâche «Indication de notation»
| Entrer | Conclusion | Limite de temps | Limite de mémoire |
|---|
| entrée standard ou input.txt | sortie standard ou output.txt | 1 seconde | 64 mégaoctets |
Galya développe un agrégateur d'avis. Elle a décidé de désigner les classements des institutions à l'aide d'étoiles à sept branches.
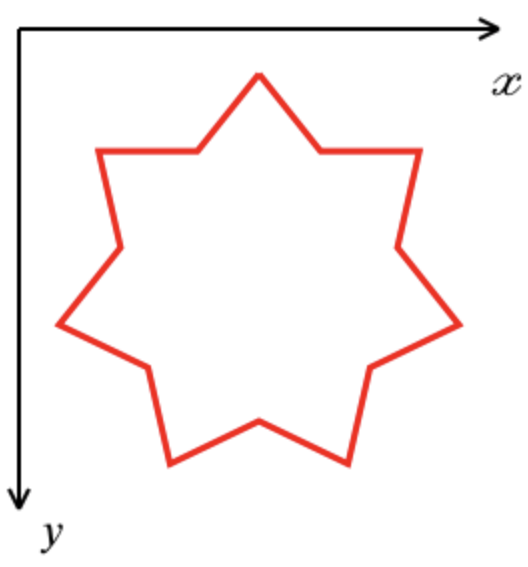
Le système de rendu d'entrée reçoit un rectangle de hauteur h et de largeur w, dont le coin supérieur gauche est situé au point (x, y). Une étoile doit être tirée selon les règles suivantes:
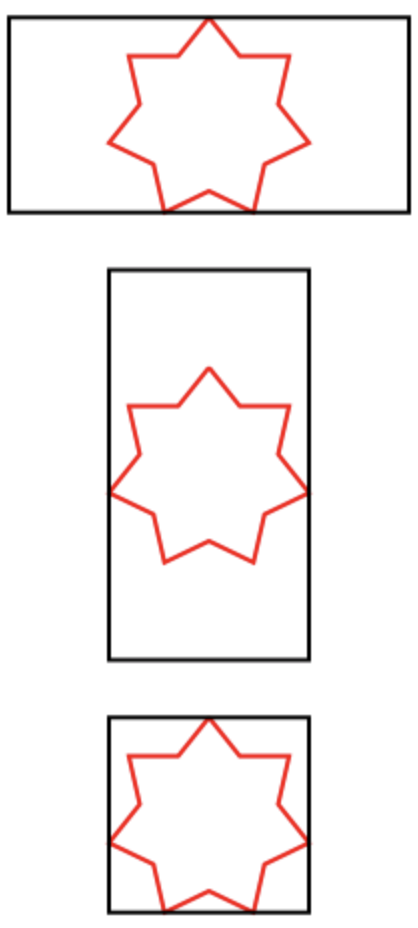
- La taille d'une étoile est déterminée par la largeur ou la hauteur du rectangle, c'est-à-dire plus petite. (Voir les dessins.)
- Si l'une des dimensions du rectangle est supérieure à la dimension correspondante de l'étoile, l'étoile doit être centrée sur cette dimension.
- L'étoile est pointée vers le haut.
Le système de rendu attend les coordonnées des sommets de l'étoile à partir du code Gali. Aidez Gale à les calculer.
Pour construire une étoile à sept pointes, Galya prend le contour extérieur de la figure obtenue en reliant les sommets d'un heptagone régulier par un. Dans le système de coordonnées, l'axe X est dirigé de gauche à droite, l'axe Y de haut en bas. Le programme Gali ne plante pas et reçoit des valeurs de largeur et de hauteur incorrectes en entrée.
Une seule ligne contient des entiers x, y, w et h, séparés par des espaces.
Exemple: l'entrée 150 0 50 100 désigne un rectangle d'une largeur de 50 points, d'une hauteur de 100 points et avec le coin supérieur gauche au point (150, 0).
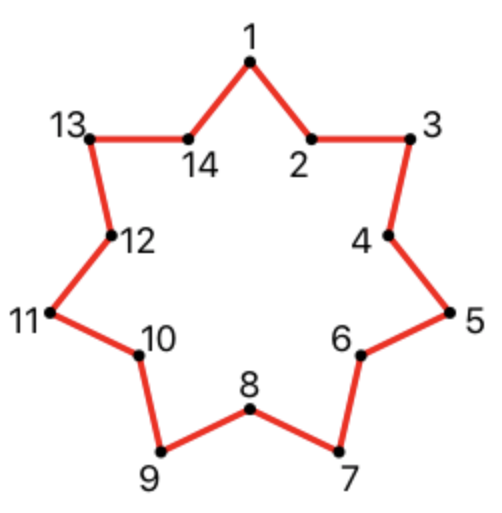
La seule ligne contenant 28 nombres séparés par des espaces est les coordonnées des sommets de l'étoile, en partant du haut puis dans le sens horaire. Les nombres doivent être arrondis à l'entier le plus proche. Consultez un exemple de sortie et une illustration du problème avant de poursuivre avec la solution.
Exemple: la sortie de trois points (1, 2), (3, 4), (5, 6) devrait ressembler à ceci: 1 2 3 4 5 6.
Des exemples
| Entrer | Conclusion |
0 0 100 100 | 50 1 65 21 90 21 85 45100 64 78 75 72 99 50 88 28 99 22 75 0 64 15 45 10 21 35 21 |
Remarques
La précision requise est de 10 chiffres significatifs.
Système de coordonnées: l'axe X est dirigé de gauche à droite, l'axe Y de haut en bas:
- Ordre des sommets attendu:
Exemples d'étoiles inscrites:
Analyse
La solution au problème se réduit à trois étapes: construire une étoile de référence avec l'orientation souhaitée dans l'espace, mettre à l'échelle les points résultants, calculer et appliquer le décalage.
Construire une étoile
La façon la plus simple est de construire une étoile inscrite dans un cercle avec un rayon unitaire centré à l'origine. Les points des sommets externes sont calculés en utilisant la trigonométrie triviale, mais avec les sommets internes, la tâche est un peu plus compliquée. Ils peuvent être trouvés de deux manières au moins. Un moyen plus simple consiste à trouver les intersections des segments reliant les sommets extérieurs. Plus compliqué est de trouver une formule pour calculer le rayon d'un cercle inscrit à partir du rayon d'un cercle circonscrit. La façon la plus simple de le faire est d'abord, par exemple, pour une étoile à 5 pointes, et généralisée à l'étoile à N points avec un espace arbitraire entre les sommets connectés.
Mise à l'échelle
Dans tous les cas, la taille est indiquée dans laquelle nous devons adapter l'étoile. Ainsi, nous devons mettre à l'échelle les points obtenus de sorte que la distance du plus à gauche au plus à droite ne dépasse pas la largeur spécifiée, et la distance du plus haut au plus bas ne dépasse pas la hauteur spécifiée. Nous prenons les facteurs d'échelle pour amener la largeur et la hauteur aux valeurs souhaitées, et sélectionnons la plus petite. Puisque nous avons prudemment construit une étoile de référence avec le centre à l'origine, il suffit de multiplier simplement les coordonnées de chaque point par le coefficient sélectionné.
Décalage
La dernière chose qui reste est de déplacer nos points pour que l'étoile soit dans les cadres donnés. Les données d'entrée de toutes les options peuvent être réduites à une boîte englobante avec une coordonnée donnée du coin supérieur gauche. Tout est simple ici: nous prenons le point le plus élevé des résultats obtenus à la dernière étape, considérons la différence de sa coordonnée y avec la coordonnée y du coin supérieur gauche et décalons tous les points verticalement de la valeur obtenue. Nous faisons de même avec la coordonnée x, il suffit de prendre non pas le point le plus haut, mais le plus à gauche. Il y a une touche finale: centrez l'étoile dans ce rectangle.
Les actions futures dépendent du coefficient que nous avons choisi à l'étape précédente:
- s'il est mis à l'échelle en hauteur - nous prenons la différence entre la largeur du rectangle et la distance de la gauche au point le plus à droite;
- s'il est mis à l'échelle en largeur - nous prenons la différence entre la hauteur du rectangle et la distance du point le plus haut au point le plus bas.
Divisez la valeur obtenue par 2 et déplacez les points en fonction de la mesure correspondante. Réponse reçue.
La tâche «Rotation et mise à l'échelle d'un cercle»
| Entrer | Conclusion | Limite de temps | Limite de mémoire |
|---|
| entrée standard ou input.txt | sortie standard ou output.txt | 1 seconde | 64 mégaoctets |
Vika développe un éditeur graphique pour smartphones et tablettes. Elle veut donner à l'utilisateur la possibilité de faire pivoter un cercle sur l'écran avec deux doigts et de changer sa taille, comme ceci:
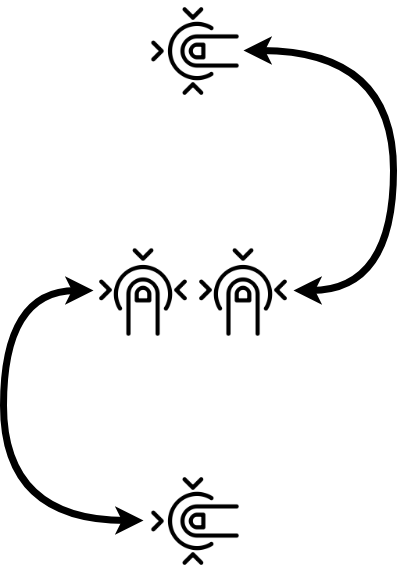
La figure pivote selon le même angle que le segment reliant les doigts. La taille de la figure change proportionnellement à la longueur du segment. Tout d'abord, la figure pivote, puis sa taille est modifiée. Initialement, le cercle a des coordonnées (x, y) et un rayon r. Une liste d'événements tactiles décrivant le geste de l'utilisateur est donnée. Aidez Vika à calculer les coordonnées finales du centre du cercle et de son rayon. Le cercle tourne par rapport au point (a, b).
La description de l'événement tactile contient l'identifiant du doigt, les coordonnées et le type d'événement. Le premier doigt auquel l'utilisateur attaché reçoit l'identifiant 0, le second - l'identifiant 1, etc.
Un exemple:
0 337 490 ACTION_DOWN - cela signifie qu'avec le doigt 0 au point (337, 490) l'événement ACTION_DOWN s'est produit.
Les événements tactiles sont des types suivants:
- ACTION_DOWN - l'utilisateur a appliqué le premier doigt sur l'écran à un moment donné.
- ACTION_POINTER_DOWN - l'utilisateur a appliqué un deuxième doigt sur l'écran à un moment donné.
- ACTION_MOVE - l'utilisateur a déplacé son doigt vers un point donné.
- ACTION_POINTER_UP - l'utilisateur a déplacé le deuxième doigt au point spécifié et l'a relâché.
- ACTION_UP - l'utilisateur a déplacé le premier doigt au point spécifié et l'a relâché.
- ACTION_CANCEL - l'utilisateur a abandonné le geste.
La première ligne contient les nombres x, y et r, séparés par des espaces. La deuxième ligne contient les nombres a et b, séparés par des espaces. Les quelques lignes suivantes contiennent des événements tactiles consécutifs.
La seule ligne avec coordonnées et rayon. Les nombres sont séparés par des espaces.
Exemple
| Entrer | Conclusion |
252 194 78
445 559
0 337 490 ACTION_DOWN
1 599 490 ACTION_POINTER_DOWN
1,576,564 ACTION_MOVE
1,552,590 ACTION_MOVE
0 407 375 ACTION_MOVE
1 505 615 ACTION_MOVE
1 482 620 ACTION_MOVE
0 477 360 ACTION_MOVE
1,435,616 ACTION_MOVE
1,411,607 ACTION_MOVE
0 547 386 ACTION_MOVE
1 364 548 ACTION_POINTER_UP
0 571 387 ACTION_UP | 831 704 73 |
Remarques
Lors de l'affichage du résultat, il est nécessaire d'arrondir toutes les valeurs à virgule flottante à une valeur entière selon les règles d'arrondi mathématique.
Analyse
Malgré le fait que le geste semble compliqué, il peut être divisé en deux composantes: rotation et mise à l'échelle. Pour faire pivoter la figure, nous devons calculer l'angle de rotation, qui peut être obtenu en utilisant la formule suivante:
a = atan2 (prevTouchX2 - prevTouchX1, prevTouchY2 - prevTouchY1) - atan2 (currentTouchX2 - currentTouchX1, currentTouchY2 - currentTouchY1).
Après avoir reçu l'angle de rotation, vous devez faire pivoter la figure elle-même, ce qui revient à tourner chaque point de la figure selon l'angle de rotation. Après avoir fait pivoter la figure, nous devons la mettre à l'échelle. La mise à l'échelle d'une figure est assez banale. Il est nécessaire de se souvenir de la distance entre les premier et deuxième doigts lors de la réception de l'événement ACTION_POINTER_DOWN pour le deuxième doigt, après quoi, en suivant la distance entre les deux premiers doigts, vous pouvez calculer le coefficient selon lequel vous devez mettre à l'échelle la figure.
La tâche "Construction de routes"
| Entrer | Conclusion | Limite de temps | Limite de mémoire |
|---|
| entrée standard ou input.txt | sortie standard ou output.txt | 1 seconde | 64 mégaoctets |
Dans un jeu mobile, le personnage principal construit une base sur une planète lointaine. Il commence par le périmètre - tours reliées par des murs laser directs. Les architectes du siège lui envoient un plan montrant n tours avec les coordonnées (x 1 , y 1 ) ... (x i , y i ) ... (x n , y n ). Du point de vue de la défense de base, cela n'a aucun sens de mettre trois ou plusieurs tours voisines sur une même ligne droite. Cependant, les architectes du personnel positionnent parfois les tours de cette manière, de sorte que le joueur lui-même doit retirer les tours intermédiaires supplémentaires.
Ayant fini avec le périmètre, le héros commence à équiper la base de l'intérieur. Il veut construire k routes entre les tours - la route peut relier deux tours non adjacentes, mais ne peut pas traverser une autre route ou un mur. Autant de routes que vous le souhaitez peuvent sortir d'une même tour.
Le héros a p robots routiers. Pour choisir le plan de construction de route optimal, le héros lui demande de trier toutes les options possibles. Les robots commencent à fonctionner simultanément et maintes et maintes fois en même temps apportent des options uniques pour l'emplacement des routes. Si avant la prochaine itération, il s'avère qu'il reste moins d'options que de robots, les robots supplémentaires sont libérés et envoyés à la cuisine pour préparer le dîner. Les robots restants terminent les dernières options et s'éteignent.
S'il s'avère que vous pouvez paver la route en dehors de la base, le héros déclare la base dangereuse et s'envole loin de la planète.
Combien de robots fonctionneront dans la cuisine?
La première ligne contient trois entiers 4 ≤ n ≤ 10 7 , 1 ≤ k ≤ n et un nombre premier 105 <p <11 × 104. Les nombres sont séparés par des espaces.
Les n lignes suivantes contiennent deux entiers 0 <x i , y i <109. Les nombres sont séparés par des espaces.
La seule ligne avec la réponse. Si la base n'est pas sûre, imprimez -1.
Exemple 1
| Entrer | Conclusion |
4 1 101363
0 0
1 0
1 1
0 1 | 101361 |
Il existe deux façons de paver la seule route: (0, 0) - (1, 1) et (1, 0) - (0, 1). Deux robots y seront engagés, et les autres iront à la cuisine: p - 2 = 101 361.
Exemple 2
| Entrer | Conclusion |
4 1 101363
1 0
2 0
0 1
1 2 | -1 |
Ici, vous pouvez construire une route entre (1, 0) - (0, 1), et c'est en dehors de la base. Le héros reconnaît que la base n'est pas sûre, la réponse est -1.
Exemple 3
| Entrer | Conclusion |
4 1 101363
0 0
1 0
2 0
0 1 | 101363 |
Les tours (0, 0), (1, 0) et (2, 0) sont sur la même ligne, donc le héros ne construira pas la tour du milieu (1, 0). Aucune route ne peut être pavée, par conséquent, tous les robots iront immédiatement à la cuisine: p = 101 363.
Analyse
Nous divisons la solution du problème en trois étapes.
La première étape consiste à déterminer pour l'ensemble de données de sommets d'entrée si le polygone est convexe et, dans l'affirmative, combien de sommets réels il possède. Un polygone est convexe si tous ses sommets sont situés sur un côté de la ligne supportant n'importe quelle arête. Pour chaque triple de sommets adjacents $ inline $ (x_ {i-1}, y_ {i-1}), (x_ {i}, y_ {i}), (x_ {i + 1}, y_ {i + 1}) $ inline $ construire quelques vecteurs $ inline $ ab = ((x_ {i-1}, y_ {i-1}), (x_ {i}, y_ {i})) et bc = ((x_ {i}, y_ {i}), (x_ {i + 1}, y_ {i + 1})) $ en ligne $ et calculez le signe de l'expression ab.x bc.y - bc.x ab.y. Si l'expression est 0, alors les sommets se trouvent sur une seule ligne droite et, selon l'état du problème, la tour se trouvant au sommet du milieu disparaît, réduisant le nombre total de tours. Si pour tous les triplets de sommets le signe du produit est 0 ou toujours le même, alors passez à la deuxième étape, sinon, nous considérons la base non sûre et imprimons la réponse -1.
Deuxième étape. Le nombre de façons de construire k diagonales disjointes à l'intérieur d'un N-gon convexe est $ en ligne $ V = 1 / (k + 1) {N-3 \ choisissez k} {N + k-1 \ choisissez k} $ en ligne $ , mais nous devons calculer l'expression p - V mod p, où p est un nombre premier.
Imaginez N! comment $ inline $ a * p ^ e $ inline $ , où le plus grand facteur commun est a, et p pgcd (a, p) = 1.
$ inline $ {n \ choose r} = (n!) / (r! (nr)!) = a_ {1} * p ^ {e_ {1}} / a_ {2} * p ^ {e_ {2} } * a_ {3} * p ^ {e_ {3}} = (a_ {1} / a_ {2} * a_ {3}) * p ^ {e_ {1} -e_ {2} -e_ {3} } $ inline $
Si $ en ligne $ e_ {1} -e_ {2} -e_ {3}> 0 $ en ligne $ , alors l'expression est divisible par p et la réponse au problème est p.
Pour le cas $ en ligne $ e_ {1} -e_ {2} -e_ {3}> 0 $ en ligne $ = 0 la réponse sera $ inline $ a_ {1} / a_ {2} * a_ {3} $ inline $ mod p.
Dans le calcul, nous prenons en compte que a b mod p = (a mod p) (b mod p) mod p, et $ inline $ k ^ {- 1} $ inline $ mod p = $ inline $ (k) ^ {p-2} $ inline $ mod p pour premier p.
Troisième étape. Pour calculer l'expression $ inline $ e_ {1} -e_ {2} -e_ {3} $ inline $ imaginez n! comme 1 2 ... p (p + 1) ... 2p (2p + 1) ..., tandis que (p + 1) ... (2p-1) mod p = 1 2 ... (p-1 ) = (p-1)! .. Total, n mod p = ( $ inline $ (p-1)! ^ k $ inline $ k (n mod p)!) mod p, où k = étage (n / p).
Tâche «Super Simple Scheduler»
| Entrer | Conclusion | Limite de temps | Limite de mémoire |
|---|
| entrée standard ou input.txt | sortie standard ou output.txt | 10 secondes | 224 mégaoctets |
Il y a n tâches à effectuer sur le processeur du smartphone. Leur mise en œuvre nécessite t 1 ... t i ... t n unités de temps, et au début de la d i- ème unité de temps, la i-ème tâche doit être terminée.
Pour être à l'heure, les tâches peuvent être effectuées dans plusieurs threads, cependant, chaque nouveau thread crée une charge croissante sur la batterie. Dans le premier flux, une unité d'énergie est consommée par unité de temps, dans la seconde unité et demie d'énergie, dans la troisième fois et demie plus que dans la seconde, etc.
Les tâches peuvent être divisées en unités de temps: d'abord, terminer partiellement l'une, puis passer à une autre, puis revenir à la première. Vous ne pouvez pas exécuter simultanément différents éléments d'une tâche dans différents threads.
Le planificateur reçoit les tâches une par une; Ayant reçu une tâche, il lui alloue immédiatement des plages horaires. Une fois la tâche distribuée, le planificateur ne peut pas la transférer vers d'autres emplacements.
Quelle quantité d'énergie sera nécessaire pour accomplir toutes les tâches si elles sont réparties de manière optimale?
La première ligne contient l'entier 1 <n ≤ 3 × 10 3 .
Les n lignes suivantes contiennent deux entiers 0 ≤ t i ≤ 10 4 et 0 ≤ d i ≤ 10 4 . Les nombres sont séparés par des espaces.
La seule ligne avec la réponse. Précision - huit décimales.
Exemple
| Entrer | Conclusion |
5
2 2
1 1
3 4
1 10
1 2 | 10.25000000 |
Analyse
Étant donné que, selon les conditions du problème, il nous suffit de calculer uniquement la quantité d'énergie consommée, nous pouvons utiliser la méthode de la solution en calculant la quantité d'énergie consommée pour chaque unité de temps. Lors de la planification de la tâche, nous prenons la valeur minimale de l'énergie consommée k = 1 et, à partir de la date limite de la tâche, nous trions tous les créneaux de l'intervalle de temps.
Si la consommation d'énergie de l'emplacement est inférieure au coefficient (k) et que cet intervalle de temps n'a pas été utilisé lors de la planification de la tâche, nous occupons cet emplacement pour terminer la tâche en augmentant le coefficient de l'emplacement de K. Lorsque nous atteignons le début de la période, nous devons augmenter le coefficient k de 1,5 fois et Répétez la recherche des plages horaires, à partir de la date limite et jusqu'à ce que la tâche soit complètement planifiée. Une fois la planification de toutes les tâches terminée, il ne reste plus qu'à calculer la consommation totale d'énergie en additionnant les coefficients obtenus de chaque unité de temps.
La tâche des objets destructibles
| Entrer | Conclusion | Limite de temps | Limite de mémoire |
|---|
| entrée standard ou input.txt | sortie standard ou output.txt | 2 secondes | 64 mégaoctets |
2D- . , : n- (x 1 , y 1 )...(x i , y i )...(x n , y n ). — , . . , — , .
, [0 1 2 3 4], 1 3 1 3, [1 2 3] [0 1 3 4].
, . . , , .
, ?
n ≤ 500. n x y. .
. — .
Exemple 1
| |
4
100 100
200 100
200 200
100 200 | 0.000000 |
Exemple 2
| |
6
167 84
421 84
283 192
433 298
164 275
320 133 | 326.986753 |
, , . « » : — . : , ( ) .
, ? ( , , ). : , , , . , , ( ) . even-odd rule: . — , ( ) , — .
, , — , . (, , ):
- ( );
- : , - ;
- ( , 10-5 );
- even-odd rule — ;
- : 180 .
«DNA»
| Conclusion | | |
|---|
| input.txt | output.txt | 8 | 128 |
, . , , . n . , . : A, T, G C. . .
n. n . . 6⋅10 6 .
. . . . . , .
( , ):
5
TTT
GAAGCT
CAAT
AGA
AGGCA
:
2 TTT
6 AGA
28 AGA
30 AGA
57 CAAT
86 AGA
100 GAAGCT
190 TTT
191 TTT
196 AGA
219 TTT
232 AGA
271 TTT
284 TTT
285 TTT
298 TTT
320 TTT
330 TTT
331 TTT
342 TTT
373 AGA
397 AGA
488 AGA
509 AGA
524 AGA
565 TTT
574 AGA
605 AGA
625 CAAT
630 AGA
681 CAAT
718 TTT
719 TTT
744 AGGCA
754 AGA
784 AGA
808 TTT
821 CAAT
833 AGA
861 CAAT
879 AGA
921 AGA
955 AGA
, . — , — . , . . , .
, .
«QR Quest»
| Conclusion | | |
|---|
| input.txt | output.txt | 1 | 64 |

t, . t n i , .
t , .
Exemple 1
| |
4
8 10 1 9 2 6 7 8
14 2 0 11 10 4 1 0
6 6 4 1 10 0 11 6
11 4 3 4 14 8 12 5 | 0
13
15
5 |
Exemple 2
| |
4
9 10 6 2 12 11 7 2
3 10 1 14 13 13 1 1
6 8 8 5 3 2 6 4
5 11 5 5 3 1 10 7 | 3
9
2
7 |
, . QR- , . - .
Au total, huit nombres ont été saisis - les coordonnées des cellules de ces tableaux, c'est-à-dire 4 paires avec les coordonnées de la colonne et de la ligne. Il a fallu deviner quelle opération était effectuée avec ces cellules et à partir de quel tableau une cellule supplémentaire.
À l'aide de manipulations simples, il a été possible de vérifier qu'il s'agit de la somme xor pour quatre cellules des tableaux A, B et C, adressée par les indices a 0 ... a 7 :
R = A [a 0 , a 1 ] ^ B [a 2 , a 3 ] ^ B [a 4 , a 5 ] ^ C [a 6 , a 7 ].