Preuve de lieux où les symétries ne peuvent exister

Une réalisation mathématique majeure a été l'hypothèse de Zimmer trouvée par une petite équipe de chercheurs.

Pour les réseaux de plus grandes dimensions de symétrie, il n'est pas toujours possible de passer aux dimensions inférieures au rang

Le succès de Robert Zimmer peut être défini de plusieurs façons. En tant que président de l'Université de Chicago depuis 2006, il a défrayé la chronique, trouvant des montants à neuf chiffres pour le financement et publiant des articles en faveur de la liberté d'expression sur le campus. Mais avant de devenir président de l'université, il était mathématicien. Et longtemps après avoir quitté la recherche sérieuse, le plan de recherche qu'il a lancé donne enfin ses résultats.

Il y a un an, trois mathématiciens ont prouvé l'hypothèse de Zimmer liée aux circonstances dans lesquelles les espaces géométriques ont des symétries d'un certain type. Leur preuve est devenue l'une des plus grandes réalisations mathématiques de ces dernières années. Cela met fin à la question qui s'est posée à Zimmer lors de son intense activité mentale à la fin des années 1970 et au début des années 1980.

"Je dirais que je me suis couché cinq ans avec des réflexions sur cette tâche, tous les soirs, donc j'étais obsédé par cela, et c'est génial de voir comment les gens l'ont résolu", a déclaré Zimmer.

Habituellement, plus l'espace de dimension géométrique est grand, plus il peut y avoir de symétries. Cela peut être imaginé en étudiant un cercle existant sur un plan bidimensionnel et une balle s'étendant en trois dimensions: il y a plus de façons de faire tourner une balle que de faire tourner un cercle. Des dimensions de balle supplémentaires créent des symétries supplémentaires.

La conjecture de Zimmer se réfère à des symétries d'un type spécial connu sous le nom de réseaux de haut rang. Elle demande si la mesure de l'espace géométrique limite l'utilisation de symétries de ce type. Les auteurs des nouveaux travaux - Aaron Brown et Sebastian Hurtado-Salazar de l'Université de Chicago et David Fisher de l'Université d'Indiana - ont montré qu'avec le nombre de mesures inférieures à certaines symétries spécifiques, on ne les observe pas. Ainsi, ils ont prouvé l'exactitude de l'hypothèse de Zimmer.


Robert Zimmer, maintenant président de l'Université de Chicago, a développé une hypothèse qui porte son nom il y a près de 40 ans

Leur travail répond à une question importante et de longue haleine, ouvrant de nouvelles façons d'en étudier bien d'autres. Il révèle également les propriétés intrinsèques des espaces géométriques. La symétrie est l'une des propriétés les plus simples de ces espaces. Le nouveau travail dit que les symétries peuvent exister dans des espaces d'un type, et ne peuvent pas dans d'autres. Cette réalisation a été obtenue après des décennies de temps d'arrêt.

«L'hypothèse semblait pouvoir occuper les gens pendant très longtemps», a déclaré Amy Wilkinson, mathématicienne à l'Université de Chicago, qui a organisé la conférence de cette année sur cette preuve. "Et ils ont relativement simplement détruit cette question."

Des symétries satisfaisantes

La symétrie est l'un des premiers concepts géométriques que les enfants rencontrent en mathématiques. De leurs propres mains, ils apprennent que vous pouvez faire pivoter, retourner et déplacer le formulaire, et finalement obtenir le même formulaire avec lequel ils ont commencé. Préserver la forme de l'objet à la suite de changements répond avec une certaine satisfaction interne - c'est un signe d'un ordre plus profond dans l'Univers.

Les mathématiciens ont leur propre langage formel pour étudier la symétrie. Il leur donne l'occasion de discuter en termes concis des différentes symétries applicables dans un espace géométrique donné.

Un carré, par exemple, a huit symétries - huit façons de le retourner ou de le faire pivoter, obtenant à nouveau le carré. Le cercle peut être tourné n'importe quel nombre de degrés; elle a un nombre infini de symétries. Les mathématiciens collectent toutes les symétries d'un objet géométrique ou d'un espace donné et les regroupent en un «groupe».

Les groupes sont intéressants en soi. Ils apparaissent souvent à la suite de l'étude de certains espaces géométriques, mais ils apparaissent parfois dans un contexte totalement étranger à la géométrie. Par exemple, les groupes peuvent former des ensembles numériques (par exemple, il y a une certaine symétrie en ajoutant 5 ou en soustrayant 5 d'un nombre).

"Un groupe, en principe, peut apparaître comme une symétrie de choses complètement différentes", a déclaré Zimmer.

Il existe des formes de symétrie plus exotiques que celles que nous étudions à l'école. Considérons, par exemple, la symétrie des réseaux. Le réseau le plus simple est une grille à deux dimensions. Dans l'avion, le réseau peut être déplacé vers le haut, le bas, la gauche, la droite de n'importe quel nombre de carrés et obtenir un réseau qui ressemble exactement à l'original. Vous pouvez également refléter la grille à travers un nombre quelconque de cellules individuelles. Les espaces avec des réseaux ont une infinité de symétries différentes de réseaux.



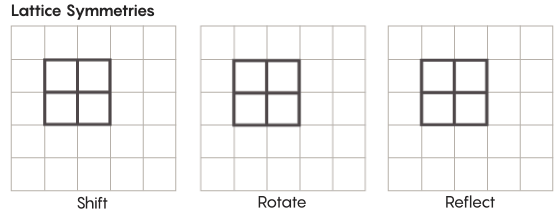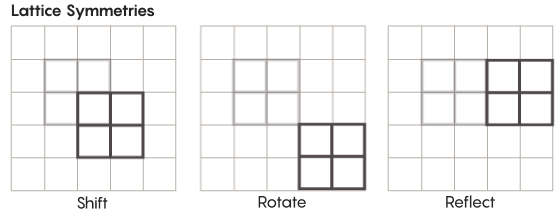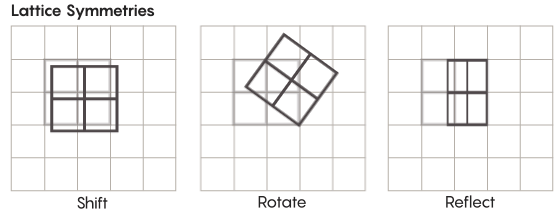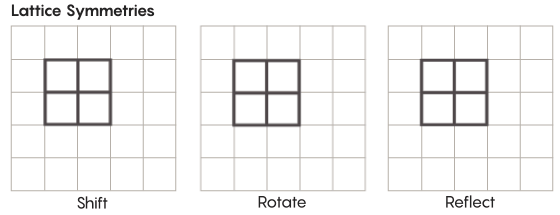
Les réseaux peuvent exister dans n'importe quel nombre de dimensions. Dans un espace tridimensionnel, un réseau peut être composé de cubes et non de carrés. En quatre dimensions ou plus, il ne sera pas possible de présenter le réseau, mais il fonctionne de la même manière; les mathématiciens peuvent le décrire exactement. Les groupes d'intérêt pour l'hypothèse de Zimmer comprennent les réseaux de «rang supérieur» ou les réseaux dans certains espaces de dimensions supérieures. "Cet étrange réseau serait très beau, s'il pouvait être vu, même s'il ne m'avait pas été donné", a déclaré Khurtado-Salazar. "Il me semble que la regarder serait très bien."

Au 20e siècle, les mathématiciens ont découvert ces groupes dans diverses conditions - non seulement en géométrie, mais aussi en théorie des nombres, en logique et en informatique. En ouvrant de nouveaux groupes, il est logique de se poser la question - quel type d'espaces possèdent de tels ensembles de symétries?

Parfois, les groupes sont évidemment impossibles à faire correspondre l'espace. On comprend assez rapidement que le groupe de symétries d'un cercle ne peut être appliqué à un carré. Faites pivoter le carré de 10 degrés et vous n'obtiendrez pas le carré d'origine. Mais un mélange d'un groupe avec un nombre infini de symétries et d'espace avec de nombreuses dimensions rend difficile de déterminer l'applicabilité du groupe.

"Lorsque nous passons à un groupe plus complexe dans plus de dimensions", a déclaré Zimmer, "ces questions deviennent très compliquées."

Connexion indirecte

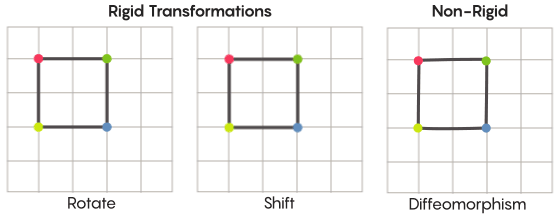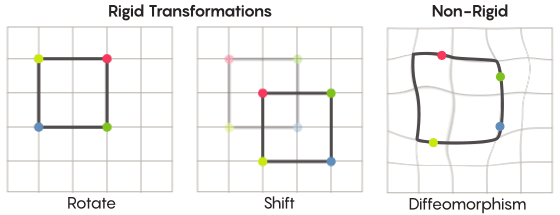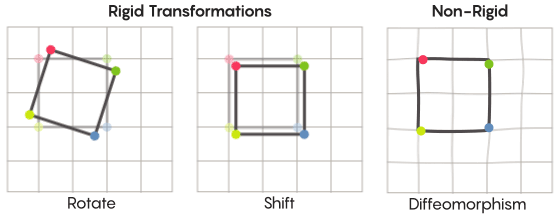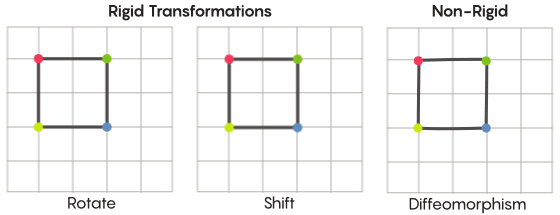
En imaginant la symétrie, nous imaginons la rotation de la forme entière - par exemple, un carré tourné à 90 degrés. Mais à un niveau de base, la symétrie dépend des points mobiles. La transformation symétrique de l'espace signifie que vous devez en prendre chaque point et le déplacer vers un autre point. En ce sens, tourner le carré de 90 degrés signifie en fait que vous devez prendre chaque point du carré et le faire pivoter de 90 degrés afin qu'il ne se trouve pas sur le bord à partir duquel vous avez commencé.


David Fisher

Le problème des points mobiles peut être résolu plus ou moins strictement. Les transformations symétriques les plus connues - la réflexion d'un carré par rapport à la diagonale ou sa rotation de 90 degrés - sont très strictes. Strict dans le sens où ils ne confondent pas les points. Les points qui étaient des sommets avant la réflexion restent des sommets après (ils deviennent simplement des sommets différents), et les points qui constituaient les bords droits, après réflexion, constituent toujours les bords droits (juste différents).

Il existe des types de transformations symétriques moins strictes et plus flexibles, et ils sont intéressants dans le contexte de l'hypothèse de Zimmer. Dans de telles transformations, les points changent plus fortement leur organisation; ils ne conservent pas nécessairement leurs anciennes relations les uns avec les autres après la transformation. Par exemple, vous pouvez déplacer chaque point du carré de trois unités de longueur le long du périmètre du carré - cela satisfait les exigences de base d'une transformation symétrique, c'est-à-dire simplement déplacer chaque point de l'espace vers un autre endroit. Aaron Brown, co-auteur de la preuve, a décrit à quoi pourraient ressembler ces transformations plus libres dans le contexte de la balle.

«Vous pouvez prendre les pôles nord et sud et les tourner dans des directions opposées. Ensuite, la distance entre les points augmentera », a déclaré Brown.

Dans le cas d'une grille, au lieu de simplement la déplacer le long du plan, vous pouvez la plier, l'étirer à certains endroits et la serrer à d'autres, de sorte que le maillage transformé ne chevauche plus celui d'origine. De telles transformations sont moins strictes et sont appelées difféomorphismes .



Zimmer avait de bonnes raisons d'utiliser cette version moins rigoureuse de la symétrie dans son hypothèse. Des grilles spéciales du rang le plus élevé liées à cette hypothèse ont été étudiées pour la première fois dans les années 1960 par Grigory Alexandrovich Margulis , qui a reçu le prix Fields pour son travail. Margulis a fait une description complète du type d'espaces pouvant être transformés à l'aide de ces réseaux de rang supérieur, si seules des transformations strictes sont autorisées.

L'hypothèse de Zimmer est devenue une continuation naturelle du travail de Margulis. Il commence par une liste d'espaces sur lesquels les réseaux de premier rang peuvent fonctionner - Margulis a découvert cette liste - et demande si cette liste s'étend si les réseaux sont autorisés à avoir des transformations moins strictes.

Dans le nouveau travail, trois mathématiciens ont prouvé que l'affaiblissement de la définition de la symétrie ne change pas la portée des symétries des réseaux d'ordre supérieur. Même si les réseaux sont autorisés à avoir des transformations très irrégulières - pour se déplacer, se plier, s'étirer - les réseaux ont toujours une restriction stricte sur la portée.

«Après avoir ajouté une telle flexibilité à l'énoncé du problème, intuitivement, bien sûr, il semble que les grilles puissent agir plus largement. Par conséquent, il s'avère surprenant qu'en réalité, la réponse sera «non» - dans certains cas, ils ne le peuvent pas », a déclaré Fisher.

Les mathématiciens ont établi des correspondances exactes entre la dimension de l'espace et la dimension, ou rang, des réseaux, pour les réseaux qui peuvent jouer le rôle de symétrie dans un espace donné. En général, ils ont montré que plus le rang du réseau est élevé, plus il faut de mesures pour l'espace qui peut l'accueillir. Même avec une flexibilité considérable dans la transformation de l'espace, les transformations des réseaux de haut rang sont limitées à des dimensions plus élevées.

"Cela suggère qu'il y a quelque chose de très fondamental dans la structure des espaces, ce qui implique leur capacité à s'adapter à de telles transformations", a déclaré Wilkinson.

L'hypothèse de Zimmer n'est que la première étape d'un programme plus vaste. Après l'avoir traité, les co-auteurs de l'ouvrage ont imposé une restriction approximative sur les espaces dans lesquels les réseaux de haut rang peuvent être transformés. La phase suivante, plus ambitieuse, des travaux sera la concentration sur les espaces dans lesquels les réseaux peuvent exister - puis la classification de toutes les différentes façons de transformer les réseaux de ces espaces.

«En fin de compte, le programme devrait être capable de classer toutes ces méthodes. Il existe de nombreuses questions intéressantes au-delà de la simple constatation de l'existence de certains endroits dans lesquels les grilles ne peuvent pas fonctionner », a déclaré Zimmer.