🔡 🤙🏿 🗜️ Julia et portraits de phases de systèmes dynamiques 🐲 👨🏾‍💼 👩🏾‍🚒

Nous continuons à maîtriser la jeune et prometteuse langue polyvalente Julia . Mais pour commencer, nous avons besoin d'une possibilité d'application très étroite - pour résoudre des problèmes typiques de physique. C'est la tactique la plus pratique pour maîtriser l'instrument: pour obtenir un coup de main, nous allons résoudre des problèmes urgents, augmenter progressivement la complexité et trouver des moyens de nous faciliter la vie. En bref, nous allons résoudre des différences et construire des graphes.

Pour commencer, téléchargez le package graphique Gadfly , et immédiatement la version complète du développeur, afin qu'il fonctionne bien avec notre Julia 1.0.1. Nous conduisons dans notre carnet REPL, JUNO ou Jupyter:

using Pkg pkg"add Compose#master" pkg"add Gadfly#master"

Ce n'est pas l'option la plus pratique, mais en attendant la mise à jour PlotlyJS , vous pouvez essayer pour la comparaison.

Vous avez également besoin d'un outil puissant pour résoudre des équations différentielles.

 ]add DifferentialEquations #

Il s'agit du package le plus complet et le plus pris en charge qui propose de nombreuses méthodes de résolution des problèmes. Passez maintenant aux portraits de phases.

Les solutions d'équations différentielles ordinaires sont souvent plus commodes à représenter sous une forme inhabituelle $y ^ 1 (t), ..., y ^ L (t)$ , et dans l' espace des phases le long des axes dont les valeurs de chacune des fonctions trouvées sont tracées. De plus, l'argument t n'est inclus dans les graphiques que de façon paramétrique. Dans le cas de deux ODE, un tel graphique - le portrait de phase du système - est une courbe sur le plan de phase et est donc particulièrement évident.

Oscillateur

Dynamique des oscillateurs harmoniques $\ gamma$ est décrit par le système d'équations suivant:

d o t x = y d o t y = - o m e g a^{2} x + g a m m a y

$\ dot {x} = y \\ \ dot {y} = - \ omega ^ 2x + \ gamma y$

et quelles que soient les conditions initiales (x0, y0), il arrive à un état d'équilibre, un point (0,0) avec un angle de déviation nul et une vitesse nulle.

À $\ gamma = 0$ la solution prend la forme caractéristique d'un oscillateur classique.

 using DifferentialEquations, Gadfly #     -    function garmosc(ω = pi, γ = 0, x0 = 0.1, y0 = 0.1) A = [0 1 -ω^2 γ] syst(u,p,t) = A * u # ODE system u0 = [x0, y0] # start cond-ns tspan = (0.0, 4pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 4) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end

Analysons le code. La fonction accepte les valeurs du paramètre de fréquence et d'atténuation, ainsi que les conditions initiales. La fonction imbriquée syst () définit le système. Pour que cela se révèle, ils ont utilisé la multiplication matricielle sur une ligne. La fonction résoudre () , prenant un grand nombre de paramètres, est configurée de manière très flexible pour résoudre le problème, mais nous avons seulement indiqué la méthode de solution - Runge-Kutta 4 ( il y en a beaucoup d'autres ), l'erreur relative et le fait que tous les points ne doivent pas être enregistrés, mais seulement tous les quatre . La matrice de réponse est stockée dans la variable sol , de plus, sol.t contient un vecteur de temps, et sol.u résout le système à ces moments. Tout cela est calmement tracé dans Plots , et pour Gadfly, vous devez compléter la réponse dans une matrice plus pratique. Nous n'avons pas besoin de temps, nous ne renvoyons donc que des solutions.

Construisons un portrait de phase:

 Ans0 = garmosc() plot(x = Ans0[:,1], y = Ans0[:,2])

Parmi les fonctions d'ordre supérieur, la broadcast(f, [1, 2, 3]) est particulièrement notable pour nous, qui substitue alternativement les valeurs du tableau [1, 2, 3] dans la fonction f . Enregistrement court f.([1, 2, 3]) . Ceci est utile pour faire varier la fréquence, le paramètre d'atténuation, les coordonnées initiales et la vitesse initiale.

Caché sous le spoiler

 L = Array{Any}(undef, 3)#     (  ) clr = ["red" "green" "yellow"] function ploter(Answ) for i = 1:3 L[i] = layer(x = Answ[i][:,1], y = Answ[i][:,2], Geom.path, Theme(default_color=clr[i]) ) end p = plot(L[1], L[2], L[3]) end Ans1 = garmosc.( [pi 2pi 3pi] )#  p1 = ploter(Ans1) Ans2 = garmosc.( pi, [0.1 0.3 0.5] )#  p2 = ploter(Ans2) Ans3 = garmosc.( pi, 0.1, [0.2 0.5 0.8] ) p3 = ploter(Ans3) Ans4 = garmosc.( pi, 0.1, 0.1, [0.2 0.5 0.8] ) p4 = ploter(Ans4) set_default_plot_size(16cm, 16cm) vstack( hstack(p1,p2), hstack(p3,p4) ) #

Maintenant, nous ne considérons pas de petites oscillations, mais des oscillations d'amplitude arbitraire:

d o t x = y d o t y = - s i n (o m e g a x) + g a m m a y

$\ dot {x} = y \\ \ dot {y} = - sin (\ omega x) + \ gamma y$

Le diagramme de phase de la solution n'est pas une ellipse (qui indique la non-linéarité de l'oscillateur). Moins nous choisissons l'amplitude des oscillations (c'est-à-dire les conditions initiales), moins la non-linéarité apparaît (par conséquent, de petites oscillations du pendule peuvent être considérées comme harmoniques).

Caché sous le spoiler

 function ungarmosc(ω = pi, γ = 0, x0 = 0.1, y0 = 0.1) function syst(du,u,p,t) du[1] = u[2] du[2] = -sin( ω*u[1] )+γ*u[2] end u0 = [x0, y0] # start cond-ns tspan = (0.0, 2pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 4) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end Ans1 = ungarmosc.( [pi 2pi 3pi] ) p1 = ploter(Ans1) Ans2 = ungarmosc.( pi, [0.1 0.4 0.7] ) p2 = ploter(Ans2) Ans3 = ungarmosc.( pi, 0.1, [0.1 0.5 0.9] ) p3 = ploter(Ans3) Ans4 = ungarmosc.( pi, 0.1, 0.1, [0.1 0.5 0.9] ) p4 = ploter(Ans4) vstack( hstack(p1,p2), hstack(p3,p4) )

Brusselator

Ce modèle décrit une certaine réaction chimique autocatalytique dans laquelle la diffusion joue un rôle. Le modèle a été proposé en 1968 par Lefebvre et Prigozhin.

d o t u_{1} = - (m u + 1) u_{1} + u_{1}^{2} u_{2} + 1 d o t u_{2} = m u u_{1} - u_{1}^{2} u_{2}

$\ dot {u} _1 = - (\ mu + 1) u_1 + u ^ 2_1u_2 + 1 \\ \ dot {u} _2 = \ mu u_1-u ^ 2_1u_2$

Fonctions inconnues $u_1 (t), \, u_2 (t)$ reflètent la dynamique de la concentration des produits intermédiaires d'une réaction chimique. Paramètre du modèle $\ mu$ la concentration initiale du catalyseur (troisième substance) est logique.

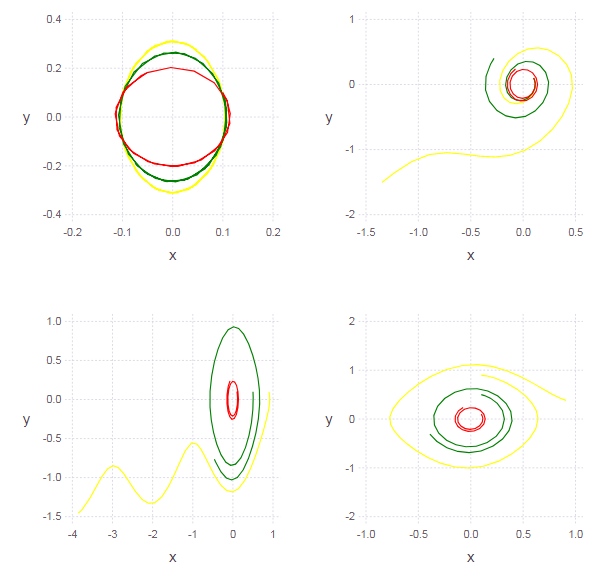
Plus en détail, l'évolution du portrait de phase du brusselator peut être observée en effectuant des calculs avec différents paramètres $\ mu$ . Avec son augmentation, le nœud se déplacera d'abord progressivement vers un point avec des coordonnées (1, $\ mu$ ) jusqu'à ce qu'il atteigne une valeur de bifurcation $\ mu$ = 2. À ce stade, il y a une restructuration qualitative du portrait, exprimée dans la naissance du cycle limite. Avec une nouvelle augmentation $\ mu$ seule une modification quantitative des paramètres de ce cycle se produit.

Caché sous le spoiler

 function brusselator(μ = 0.1, u0 = [0.1; 0.1]) function syst(du,u,p,t) du[1] = -(μ+1)*u[1] + u[1]*u[1]*u[2] + 1 du[2] = μ*u[1] - u[1]*u[1]*u[2] end tspan = (0.0, 10) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 1) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end L = Array{Any}(undef, 10) function ploter(Answ) for i = 1:length(Answ) L[i] = layer(x = Answ[i][:,1], y = Answ[i][:,2], Geom.path ) end plot(L[1], L[2], L[3], L[4], L[5], L[6], L[7], L[8], L[9], L[10]) end SC = [ [0 0.5], [0 1.5], [2.5 0], [1.5 0], [0.5 1], [1 0], [1 1], [1.5 2], [0.1 0.1], [0.5 0.2] ] Ans1 = brusselator.( 0.1, SC ) Ans2 = brusselator.( 0.8, SC ) Ans3 = brusselator.( 1.6, SC ) Ans4 = brusselator.( 2.5, SC ) p1 = ploter(Ans1) p2 = ploter(Ans2) p3 = ploter(Ans3) p4 = ploter(Ans4) set_default_plot_size(16cm, 16cm) vstack( hstack(p1,p2), hstack(p3,p4) )

Assez pour aujourd'hui. La prochaine fois, nous essaierons d'apprendre à utiliser un autre package graphique pour de nouvelles tâches, tout en tapant simultanément notre main sur la syntaxe de Julia. Dans le processus de résolution des problèmes, qui commence lentement à être tracé, pas que les avantages et les inconvénients soient simples ... plutôt, les commodités et les inconvénients - une conversation distincte devrait être consacrée à cela. Et, bien sûr, j'aimerais voir quelque chose de plus sérieux sur mon habra que mes jeux avec des fonctions - par conséquent, j'exhorte les julistes à en dire plus sur des projets plus sérieux, cela aiderait beaucoup, et en particulier, à apprendre cette merveilleuse langue.

Julia et portraits de phases de systèmes dynamiques

Oscillateur

Brusselator

More articles: