👸🏾 🕉️ 🦄 Julia et équations aux dérivées partielles 🧒🏿 🤣 📊

Sur l'exemple des modèles physiques les plus typiques, nous consoliderons les compétences de travail avec les fonctions et nous familiariserons avec le visualiseur PyPlot rapide, pratique et beau, qui fournit toute la puissance du Matplotlib Python. Il y aura beaucoup de photos (cachées sous les spoilers)

Nous nous assurons que tout est propre et frais sous le capot:

Sous le capot

]status Status `C:\Users\\.julia\environments\v1.0\Project.toml` [537997a7] AbstractPlotting v0.9.0 [ad839575] Blink v0.8.1 [159f3aea] Cairo v0.5.6 [5ae59095] Colors v0.9.5 [8f4d0f93] Conda v1.1.1 [0c46a032] DifferentialEquations v5.3.1 [a1bb12fb] Electron v0.3.0 [5789e2e9] FileIO v1.0.2 [5752ebe1] GMT v0.5.0 [28b8d3ca] GR v0.35.0 [c91e804a] Gadfly v1.0.0+ #master (https://github.com/GiovineItalia/Gadfly.jl.git) [4c0ca9eb] Gtk v0.16.4 [a1b4810d] Hexagons v0.2.0 [7073ff75] IJulia v1.13.0+ [`C:\Users\\.julia\dev\IJulia`] [6218d12a] ImageMagick v0.7.1 [c601a237] Interact v0.9.0 [b964fa9f] LaTeXStrings v1.0.3 [ee78f7c6] Makie v0.9.0+ #master (https://github.com/JuliaPlots/Makie.jl.git) [7269a6da] MeshIO v0.3.1 [47be7bcc] ORCA v0.2.0 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.0+ #master (https://github.com/sglyon/PlotlyJS.jl.git) [91a5bcdd] Plots v0.21.0 [438e738f] PyCall v1.18.5 [d330b81b] PyPlot v2.6.3 [c4c386cf] Rsvg v0.2.2 [60ddc479] StatPlots v0.8.1 [b8865327] UnicodePlots v0.3.1 [0f1e0344] WebIO v0.4.2 [c2297ded] ZMQ v1.0.0

Sinon, nous aurons tout ce dont nous avons besoin pour aujourd'hui

 julia>] pkg> add PyCall pkg> add LaTeXStrings pkg> add PyPlot pkg> build PyPlot #     build #    -      ,    pkg> add Conda #    Jupyter -    pkg> add IJulia #      pkg> build IJulia #     build

Passons maintenant aux tâches!

Porter l'équation

En physique, le terme transfert est compris comme signifiant des processus irréversibles, à la suite desquels un mouvement spatial (transfert) de masse, d'élan, d'énergie, de charge ou d'une autre quantité physique se produit dans le système physique.
L'équation de transport linéaire unidimensionnelle (ou l'équation d'advection) - l'équation différentielle partielle la plus simple - s'écrit

$\ frac {\ partial U (x, t)} {\ partial t} + c \ frac {\ partial U (x, t)} {\ partial x} = \ Phi (U, x, t)$

Pour la solution numérique de l'équation de transport, vous pouvez utiliser le schéma de différence explicite:

$\ frac {\ hat {U} _i-U_i} {\ tau} + c \ frac {U_i-U_ {i-1}} {\ Delta} = \ frac {\ Phi_ {i-1} + \ Phi_i} {2}$

où $\ chapeau {U}$ - la valeur de la fonction de grille sur la couche temporelle supérieure. Ce circuit est stable avec le numéro Courant. $K = c \ tau / \ Delta <1$

Transfert non linéaire

$\ frac {\ partial U (x, t)} {\ partial t} + (C_0 + UC_1) \ frac {\ partial U (x, t)} {\ partial x} = \ Phi (U, x, t )$

Source linéaire (transfert d'absorption): $\ Phi (U, x, t) = - BU$ . Nous utilisons le schéma de différence explicite:

$U ^ {j + 1} _i = \ left (1- \ frac {h_tB} {2} - \ frac {h_tC_0} {h_x} - \ frac {h_tC_1} {h_x} U ^ j_i \ right) U ^ j_i + U ^ j_ {i-1} \ left (\ frac {h_tC_0} {h_x} - \ frac {h_tB} {2} + \ frac {h_tC_1} {h_x} U ^ j_i \ right)$

 using Plots pyplot() a = 0.2 b = 0.01 ust = x -> x^2 * exp( -(xa)^2/b ) #   bord = t -> 0. #  #    - function transferequi(;C0 = 1., C1 = 0., B = 0., Nx = 50, Nt = 50, tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt b0 = 0.5B*dt c0 = C0*dt/dx c1 = C1*dt/dx print("Kurant: $c0 $c1") x = [i for i in range(0, length = Nx, step = dx)]#         t = [i for i in range(0, length = Nt, step = dt)] #   -   U = zeros(Nx, Nt) U[:,1] = ust.(x) U[1,:] = bord.(t) for j = 1:Nt-1, i = 2:Nx U[i, j+1] = ( 1-b0-c0-c1*U[i,j] )*U[i,j] + ( c0-b0+c1*U[i,j] )*U[i-1,j] end t, x, U end t, X, Ans0 = transferequi( C0 = 4., C1 = 1., B = 1.5, tlmt = 0.2 ) plot(X, Ans0[:,1], lab = "t1") plot!(X, Ans0[:,10], lab = "t10") p = plot!(X, Ans0[:,40], lab = "t40") plot( p, heatmap(t, X, Ans0) ) #

Résultat

Augmentons l'absorption:

 t, X, Ans0 = transferequi( C0 = 2., C1 = 1., B = 3.5, tlmt = 0.2 ) plot(X, Ans0[:,1]) plot!(X, Ans0[:,10]) p = plot!(X, Ans0[:,40]) plot( p, heatmap(t, X, Ans0) )

Résultat

 t, X, Ans0 = transferequi( C0 = 1., C1 = 15., B = 0.1, Nx = 100, Nt = 100, tlmt = 0.4 ) plot(X, Ans0[:,1]) plot!(X, Ans0[:,20]) plot!(X, Ans0[:,90])

Presque renversé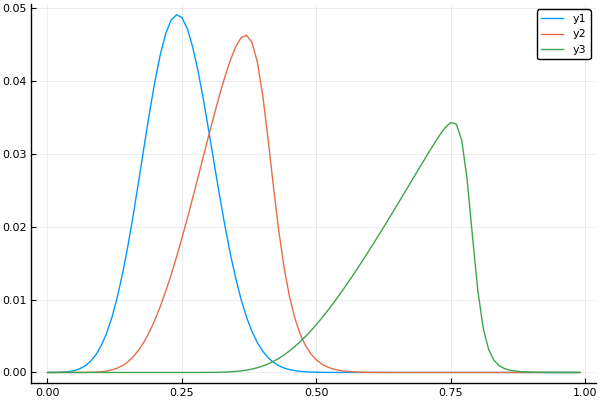

heatmap(t, X, Ans0)

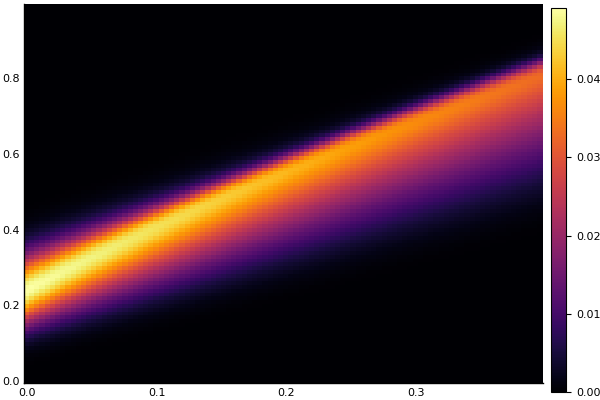
Équation de chaleur

L'équation de chaleur différentielle (ou l'équation de diffusion de chaleur) s'écrit comme suit:

$\ frac {\ partial T (x, t)} {\ partial t} + D \ frac {\ partial ^ 2 U (x, t)} {\ partial x ^ 2} = \ phi (T, x, t )$

Il s'agit d'une équation parabolique contenant la première dérivée par rapport au temps t et la seconde par rapport à la coordonnée spatiale x. Il décrit la dynamique de température, par exemple, d'une tige métallique de refroidissement ou de chauffage (la fonction T décrit le profil de température le long de la coordonnée x le long de la tige). Le coefficient D est appelé coefficient de conductivité thermique (diffusion). Il peut être constant ou dépendre, à la fois explicitement des coordonnées et de la fonction souhaitée D (t, x, T) elle-même.

Considérons l'équation linéaire (le coefficient de diffusion et les sources de chaleur sont indépendants de la température). L'approximation de différence d'une équation différentielle utilisant les schémas d'Euler explicites et implicites, respectivement:

$\ frac {T_ {i, n + 1} -T_ {i, n}} {\ tau} = D \ frac {T_ {i-1, n} -2T_ {i, n} + T_ {i + 1 , n}} {\ Delta ^ 2} + \ phi_ {i, n} \\ \ frac {T_ {i, n + 1} -T_ {i, n}} {\ tau} = D \ frac {T_ { i-1, n + 1} -2T_ {i, n + 1} + T_ {i + 1, n + 1}} {\ Delta ^ 2} + \ phi_ {i, n}$

 δ(x) = x==0 ? 0.5 : x>0 ? 1 : 0 # -     startcond = x-> δ(x-0.45) - δ(x-0.55) #   bordrcond = x-> 0. #    D(u) = 1 #   Φ(u) = 0 #    #      LaTex    Tab # \delta press Tab -> δ function linexplicit(Nx = 50, Nt = 40; tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt k = dt/(dx*dx) print("Kurant: $k dx = $dx dt = $dt k<0.5? $(k<0.5)") x = [i for i in range(0, length = Nx, step = dx)] #         t = [i for i in range(0, length = Nt, step = dt)] #   -   U = zeros(Nx, Nt) U[: ,1] = startcond.(x) U[1 ,:] = U[Nt,:] = bordrcond.(t) for j = 1:Nt-1, i = 2:Nx-1 U[i, j+1] = U[i,j]*(1-2k*D( U[i,j] )) + k*U[i-1,j]*D( U[i-1,j] ) + k*U[i+1,j]*D( U[i+1,j] ) + dt*Φ(U[i,j]) end t, x, U end t, X, Ans2 = linexplicit( tlmt = 0.005 ) plot(X, Ans2[:,1], lab = "t1") plot!(X, Ans2[:,10], lab = "t10") p = plot!(X, Ans2[:,40], lab = "t40", title = "Explicit scheme") plot( p, heatmap(t, X, Ans2) )

Résultat

Nous utilisons le schéma implicite et la méthode de balayage

 function nonexplicit(Nx = 50, Nt = 40; tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt k = dt/(dx*dx) print("Kurant: $k dx = $dx dt = $dt k<0.5? $(k<0.5)\n") x = [i for i in range(0, length = Nx, step = dx)] t = [i for i in range(0, length = Nt, step = dt)] U = zeros(Nx, Nt) η = zeros(Nx+1) ξ = zeros(Nx) U[: ,1] = startcond.(x) U[1 ,:] = bordrcond.(t) U[Nt,:] = bordrcond.(t) for j = 1:Nt-1 b = -1 - 2k*D( U[1,j] ) c = -k*D( U[2,j] ) d = U[1,j] + dt*Φ(U[1,j]) ξ[2] = c/b η[2] = -d/b for i = 2:Nx-1 a = -k*D( U[i-1,j] ) b = -2k*D( U[i,j] ) - 1 c = -k*D( U[i+1,j] ) d = U[i,j] + dt*Φ(U[i,j]) ξ[i+1] = c / (ba*ξ[i]) η[i+1] = (a*η[i]-d) / (ba*ξ[i]) end U[Nx,j+1] = η[Nx] for i = Nx:-1:2 U[i-1,j+1] = ξ[i]*U[i,j+1] + η[i] end end t, x, U end plot(X, Ans2[:,1], lab = "ex_t1") plot!(X, Ans2[:,10], lab = "ex_t10") plot!(X, Ans2[:,40], lab = "ex_t40") plot!(X, Ans3[:,1], lab = "non_t1") plot!(X, Ans3[:,10], lab = "non_t10") plot!(X, Ans3[:,40], lab = "non_t40", title = "Comparison schemes")

Comparaison de circuits

Équation de chaleur non linéaire

Des solutions beaucoup plus intéressantes peuvent être obtenues pour l'équation de chaleur non linéaire, par exemple, avec une source de chaleur non linéaire $\ phi (x, T) = 10 ^ 3 (T-T ^ 3)$ . Si vous le définissez sous cette forme, vous obtenez une solution sous forme de fronts thermiques, se propageant des deux côtés de la zone de chauffage primaire

 Φ(u) = 1e3*(uu^3) t, X, Ans4 = linexplicit( tlmt = 0.005 ) plot(X, Ans4[:,1], lab = "ex_t1") plot!(X, Ans4[:,10], lab = "ex_t10") plot!(X, Ans4[:,40], lab = "ex_t40", title = "Thermal front")

Front thermique

Des solutions encore plus inattendues sont également possibles avec la non-linéarité du coefficient de diffusion. Par exemple, si vous prenez $D (x, T) = T ^ 2$ , un $\ phi (x, T) = 10 ^ 3T ^ {3,5}$ , alors on peut observer l'effet de la combustion du milieu, localisé dans la région de son chauffage primaire (mode S de combustion «avec exacerbation»).
Dans le même temps, nous vérifierons comment notre schéma implicite fonctionne avec la non-linéarité des sources et le coefficient de diffusion

 D(u) = u*u Φ(u) = 1e3*abs(u)^(3.5) t, X, Ans5 = linexplicit( tlmt = 0.0005 ) t, X, Ans6 = nonexplicit( tlmt = 0.0005 ) plot(X, Ans5[:,1], lab = "ex_t1") plot!(X, Ans5[:,10], lab = "ex_t10") p1 = plot!(X, Ans5[:,40], lab = "ex_t40", title = "Burning with aggravation") p2 = heatmap(abs.(Ans6-Ans5), title = "Difference") #      plot(p1, p2)

Mode S

Équation d'onde

Équation d'onde hyperbolique

$\ frac {\ partial ^ 2 U (x, t)} {\ partial t ^ 2} = c ^ 2 \ frac {\ partial ^ 2 U (x, t)} {\ partial x ^ 2}$

décrit des ondes linéaires unidimensionnelles sans dispersion. Par exemple, les vibrations d'une corde, le son dans un liquide (gaz) ou les ondes électromagnétiques dans le vide (dans ce dernier cas, l'équation doit être écrite sous forme vectorielle).

Le schéma de différence le plus simple se rapprochant de cette équation est un schéma explicite à cinq points

$\ frac {U ^ {n + 1} _i-2U ^ {n} _i + U ^ {n-1} _i} {\ tau ^ 2} = c ^ 2 \ frac {U ^ n_ {i + 1} -2U ^ n_i + U ^ n_ {i-1}} {h ^ 2} \\ x_i = ih, \, t_n = \ tau$

Ce schéma, appelé "croix", a un deuxième ordre de précision dans le temps et les coordonnées spatiales et est à trois couches dans le temps.

 #     ψ = x -> x^2 * exp( -(x-0.5)^2/0.01 ) #    ϕ(x) = 0 c = x -> 1 #     function pdesolver(N = 100, K = 100, L = 2pi, T = 10, a = 0.1 ) dx = L/N; dt = T/K; gam(x) = c(x)*c(x)*a*a*dt*dt/dx/dx; print("Kurant-Fridrihs-Levi: $(dt*a/dx) dx = $dx dt = $dt") u = zeros(N,K); x = [i for i in range(0, length = N, step = dx)] #      u[:,1] = ψ.(x); u[:,2] = u[:,1] + dt*ψ.(x); #     fill!( u[1,:], 0); fill!( u[N,:], ϕ(L) ); for t = 2:K-1, i = 2:N-1 u[i,t+1] = -u[i,t-1] + gam( x[i] )* (u[i-1,t] + u[i+1,t]) + (2-2*gam( x[i] ) )*u[i,t]; end x, u end N = 50; #     K = 40; #    a = 0.1; #    L = 1; #   T = 1; #   t = [i for i in range(0, length = K, stop = T)] X, U = pdesolver(N, K, L, T, a) #    plot(X, U[:,1]) plot!(X, U[:,40])

Résultat

Pour construire une surface, nous utiliserons PyPlot comme environnement Plots, mais directement:

Graphique de surface

 using PyPlot surf(t, X, U)

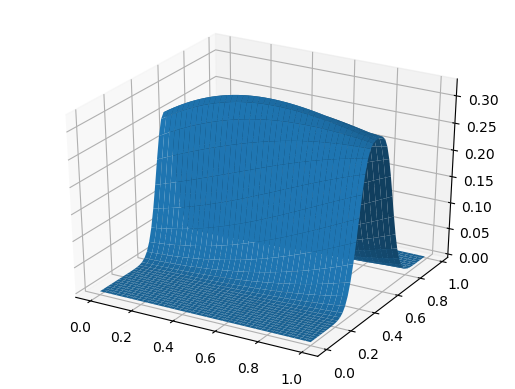
Et pour le dessert, la vague se propage à une vitesse dépendant des coordonnées:

 ψ = x -> x>1/3 ? 0 : sin(3pi*x)^2 c = x -> x>0.5 ? 0.5 : 1 X, U = pdesolver(400, 400, 8, 1.5, 1) plot(X, U[:,1]) plot!(X, U[:,40]) plot!(X, U[:,90]) plot!(X, U[:,200], xaxis=("  ", (0, 1.5), 0:0.5:2) )

Résultat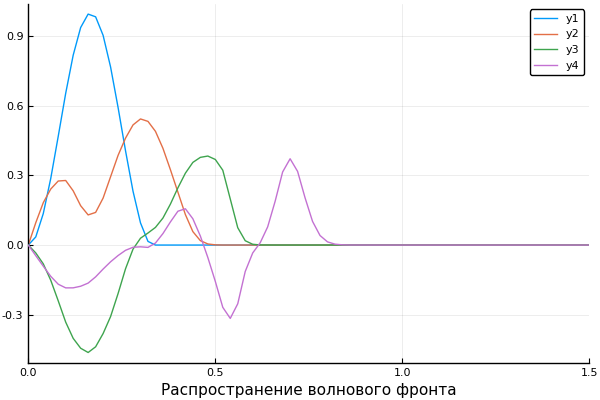

 U2 = [ U[i,j] for i = 1:60, j = 1:size(U,2) ] #    surf(U2) #

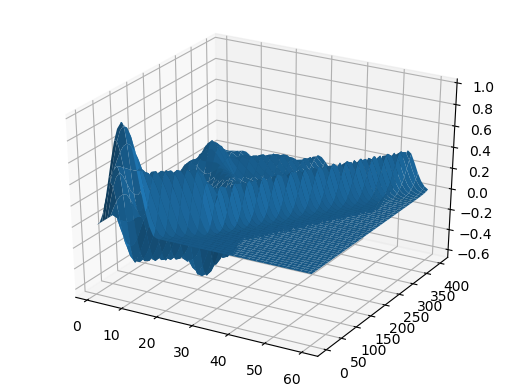
heatmap(U, yaxis=(" ", (0, 50), 0:10:50))

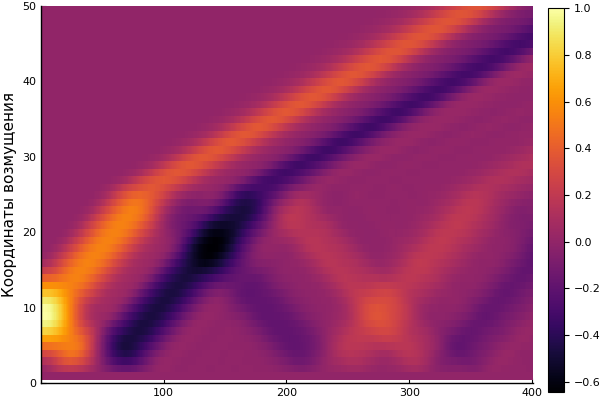
Assez pour aujourd'hui. Pour un examen plus détaillé:
Lien PyPlot vers github , d' autres exemples d'utilisation de Plots comme environnement et un bon mémo en langue russe de Julia .

Julia et équations aux dérivées partielles

Porter l'équation

Transfert non linéaire

Équation de chaleur

Équation de chaleur non linéaire

Équation d'onde

More articles: