Un auto-encodeur variationnel (auto-encoder) est un modèle génératif qui apprend à afficher des objets dans un espace caché donné.

Vous êtes-vous déjà demandé comment fonctionne un modèle d'auto-encodeur variationnel (VAE)? Vous voulez savoir comment VAE génère de nouveaux exemples comme l'ensemble de données sur lequel il a été formé? Après avoir lu cet article, vous aurez une compréhension théorique du fonctionnement interne de la VAE, et vous pourrez également l'implémenter vous-même. Ensuite, je montrerai le code VAE fonctionnel formé sur un ensemble de chiffres manuscrits, et nous nous amuserons à générer de nouveaux chiffres!

Modèles génératifs

La VAE est un modèle génératif - elle estime la densité de probabilité (PDF) des données d'entraînement. Si un tel modèle est formé aux images naturelles, il attribuera une valeur de probabilité élevée à l'image du lion et une valeur faible à l'image des conneries aléatoires.

Le modèle VAE sait également prendre des exemples à partir de PDF formés, ce qui est le plus cool, car il peut générer de nouveaux exemples similaires à l'ensemble de données d'origine!

Je vais expliquer VAE en utilisant le jeu de nombres manuscrits MNIST . Les données d'entrée pour le modèle sont des images au format $$$\ mathbb {R} ^ {28 × 28}$. Le modèle doit évaluer la probabilité d'apparition d'un chiffre comme un chiffre.

Tâche de modélisation d'image

L'interaction entre pixels est une tâche difficile. Si les pixels sont indépendants les uns des autres, vous devez étudier le PDF de chaque pixel indépendamment, ce qui est facile. La sélection est également simple - nous prenons chaque pixel séparément.

Mais dans les images numériques, il existe des dépendances claires entre les pixels. Si vous voyez le début des quatre sur la moitié gauche, vous serez très surpris si la moitié droite est l'achèvement de zéro. Mais pourquoi? ..

Espace caché

Vous savez que chaque image a un numéro. Entrée à $$$\ mathbb {R} ^ {28 × 28}$ne contient clairement pas ces informations. Mais ça doit être quelque part ... Ce "quelque part" est un espace caché.



Vous pouvez considérer l'espace caché comme $$$\ mathbb {R} ^ {k}$où chaque vecteur contient $$$k$éléments d'information nécessaires pour rendre une image. Supposons que la première dimension contienne un nombre représenté par un chiffre. La deuxième dimension peut être la largeur. Le troisième est l'angle, et ainsi de suite.

Nous pouvons imaginer le processus de dessin d'une personne en deux étapes. Premièrement, une personne détermine - consciemment ou non - tous les attributs du nombre qui va être affiché. Ensuite, ces décisions sont transformées en traits sur papier.

VAE tente de simuler ce processus: pour une image donnée $$$x$nous voulons trouver au moins un vecteur caché qui puisse le décrire; un vecteur contenant des instructions pour générer $$$x$. En le formulant par la formule de la probabilité totale , nous obtenons $$$P (x) = \ int P (x | z) P (z) dz$.

Mettons un certain sens raisonnable dans cette équation:

• Intégrale signifie que les candidats doivent être recherchés dans tous les espaces cachés.
• Pour chaque candidat $$$z$nous posons la question: est-il possible de générer $$$x$en utilisant des instructions $$$z$? Est-il assez grand $$$P (x | z)$? Par exemple, si $$$z$code les informations sur le chiffre 7, puis l'image 8 n'est pas possible. Cependant, l'image 1 est acceptable car 1 et 7 sont similaires.
• Nous en avons trouvé un bon. $$$z$? Super! Mais attendez une seconde ... combien ça coûte $$$z$probablement? $$$P (z)$assez grand? Considérons l'image du nombre inversé 7. Une correspondance idéale serait un vecteur caché décrivant la vue 7, où la taille de l'angle est réglée à 180 °. Cependant, $$$z$C'est peu probable, car généralement les nombres ne sont pas écrits à un angle de 180 °.

L'objectif de la formation VAE est de maximiser $$$P (x)$. Nous modéliserons $$$P (x | z)$utilisant une distribution gaussienne multidimensionnelle $$$\ mathcal {N} (f (z), \ sigma ^ 2 \ cdot I)$.

$$$f (z)$modélisé à l'aide d'un réseau neuronal. $$$\ sigma$Est un hyperparamètre pour multiplier la matrice d'identité $$$I$.

Gardez à l'esprit que $$$f$- c'est ce que nous allons utiliser pour générer de nouvelles images en utilisant un modèle formé. Le chevauchement d'une distribution gaussienne est uniquement à des fins éducatives. Si nous prenons la fonction delta de Dirac (c'est-à-dire déterministe $$$x = f (z)$), alors nous ne pourrons pas entraîner le modèle en descente de gradient!

Les merveilles de l'espace caché

L'approche de l'espace caché pose deux gros problèmes:

1. Quelles informations contient chaque dimension? Certaines dimensions peuvent se rapporter à des éléments abstraits, tels que le style. Même s'il était facile d'interpréter toutes les dimensions, nous ne voulons pas attribuer d'étiquettes à l'ensemble de données. Cette approche ne s'adapte pas à d'autres ensembles de données.
2. L'espace caché peut être confondu lorsqu'il existe une corrélation entre les dimensions. Par exemple, un nombre dessiné très rapidement peut conduire simultanément à l'apparition de traits angulaires et plus fins. La définition de ces dépendances est difficile.

L'apprentissage en profondeur vient à la rescousse

Il s'avère que chaque distribution peut être générée en appliquant une fonction assez complexe à la distribution gaussienne multidimensionnelle standard.

Choisissez $$$P (z)$comme une distribution gaussienne multidimensionnelle standard. Ainsi modélisé par un réseau de neurones $$$f$peut être divisé en deux phases:

1. Les premières couches cartographient la distribution gaussienne dans la vraie distribution sur l'espace caché. Nous ne pouvons pas interpréter les mesures, mais cela n'a pas d'importance.
2. Les calques suivants seront affichés à partir de l'espace caché dans $$$P (x | z)$.

Alors, comment entraînons-nous cette bête?

Formule pour $$$P (x)$insoluble, nous l'approximons donc par la méthode de Monte Carlo:

1. Sélection $$$\ {z_i \} _ {i = 1} ^ n$ du précédent $$$P (z)$
2. Rapprochement avec $$$P (x) \ approx \ frac {1} {n} \ sum_ {i = 1} ^ n P (x | z_i)$

Super! Alors essayez juste beaucoup de différents $$$z$et commencez la fête de propagation des bogues!

Malheureusement depuis $$$x$très multidimensionnelle, pour obtenir une approximation raisonnable, de nombreux échantillons sont nécessaires. Je veux dire si vous essayez $$$z$, alors quelles sont les chances d'obtenir une image qui ressemble à quelque chose $$$x$? Cela explique d'ailleurs pourquoi $$$P (x | z)$doit attribuer une valeur de probabilité positive à toute image possible, sinon le modèle ne pourra pas apprendre: échantillonnage $$$z$se traduira par une image qui est presque certainement différente de $$$x$, et si la probabilité est 0, les gradients ne pourront pas se propager.

Comment résoudre ce problème?

Coupez le chemin!

La plupart des échantillons $$$z$rien ne sera ajouté de la sélection à $$$P (x)$- Ils sont trop loin au-delà de ses frontières. Maintenant, si vous saviez à l'avance d'où les prendre ...

Peut entrer $$$Q (z | x)$. Étant donné $$$Q$seront formés pour attribuer des valeurs de probabilité élevées à $$$z$susceptibles de générer $$$x$. Vous pouvez maintenant effectuer une évaluation en utilisant la méthode de Monte Carlo, en prélevant beaucoup moins d'échantillons $$$Q$.

Malheureusement, un nouveau problème se pose! Au lieu de maximiser $$$P (x) = \ int P (x | z) P (z) dz = \ mathbb {E} _ {z \ sim P (z)} P (x | z)$nous maximisons $$$\ mathbb {E} _ {z \ sim Q (z | x)} P (x | z)$. Comment sont-ils liés les uns aux autres?

Conclusion variationnelle

La conclusion variationnelle fait l'objet d'un article séparé, je ne m'y attarderai donc pas ici en détail. Je peux seulement dire que ces distributions sont liées par cette équation:

$$

$$log P (X) - \ mathcal {KL} [Q (z | x) || P (z | x)] = \ mathbb {E} _ {z \ sim Q (z | x)} [log P (x | z)] - \ mathcal {KL} [Q (z | x) || P (z)]$$

$$$\ mathcal {KL}$est la distance de Kullback - Leibler , qui évalue intuitivement la similitude des deux distributions.

Dans un instant, vous verrez comment maximiser le côté droit de l'équation. Dans ce cas, le côté gauche est également maximisé:

• $$$P (x)$maximisé.
• jusqu'où $$$Q (z | x)$de $$$P (z | x)$- réel a priori inconnu - sera minimisé.

La signification du côté droit de l'équation est que nous avons ici des tensions:

1. D'une part, nous voulons maximiser la qualité $$$x$doit être décodé $$$z \ sim Q$.
2. D'un autre côté, nous voulons $$$Q (z | x)$( encodeur ) était similaire au précédent $$$P (z)$(distribution gaussienne multidimensionnelle). Cela peut être considéré comme une régularisation.

Minimisation de la divergence $$$\ mathcal {KL}$effectué facilement avec la bonne sélection de distributions. Nous simulerons $$$Q (z | x)$comme un réseau de neurones dont la sortie est les paramètres d'une distribution gaussienne multidimensionnelle:

• moyenne $$$\ mu_Q$
• matrice de covariance diagonale $$$\ Sigma_Q$

Puis divergence $$$\ mathcal {KL}$devient analytiquement résoluble, ce qui est excellent pour nous (et pour les gradients).

La partie décodeur est un peu plus compliquée. À première vue, je voudrais dire que ce problème est insoluble par la méthode de Monte Carlo. Mais l'échantillon $$$z$de $$$Q$ne permettra pas aux dégradés de se propager à travers $$$Q$, car la sélection n'est pas une opération différenciable. C'est un problème, car alors les poids des couches émettant $$$\ Sigma_Q$et $$$\ mu_Q$.

Nouvelle astuce de paramétrage

Nous pouvons remplacer $$$Q$transformation paramétrisée déterministe d'une variable aléatoire non paramétrique:

1. Un échantillon de la distribution gaussienne standard (sans paramètres).
2. Multiplier l'échantillon par la racine carrée $$$\ Sigma_Q$.
3. Ajout au résultat $$$\ mu_Q$.

Par conséquent, nous obtenons une distribution égale à $$$Q$. Maintenant, l'opération de récupération provient de la distribution gaussienne standard. Par conséquent, les gradients peuvent se propager à travers $$$\ Sigma_Q$et $$$\ mu_Q$puisque maintenant ce sont des voies déterministes.

Résultat? Le modèle pourra apprendre à ajuster les paramètres $$$Q$: elle va se concentrer sur le bien $$$z$qui sont capables de produire $$$x$.

Tout mettre ensemble

Le modèle VAE peut être difficile à comprendre. Nous avons examiné beaucoup de documents difficiles à digérer.

Permettez-moi de résumer toutes les étapes de la mise en œuvre de la VAE.



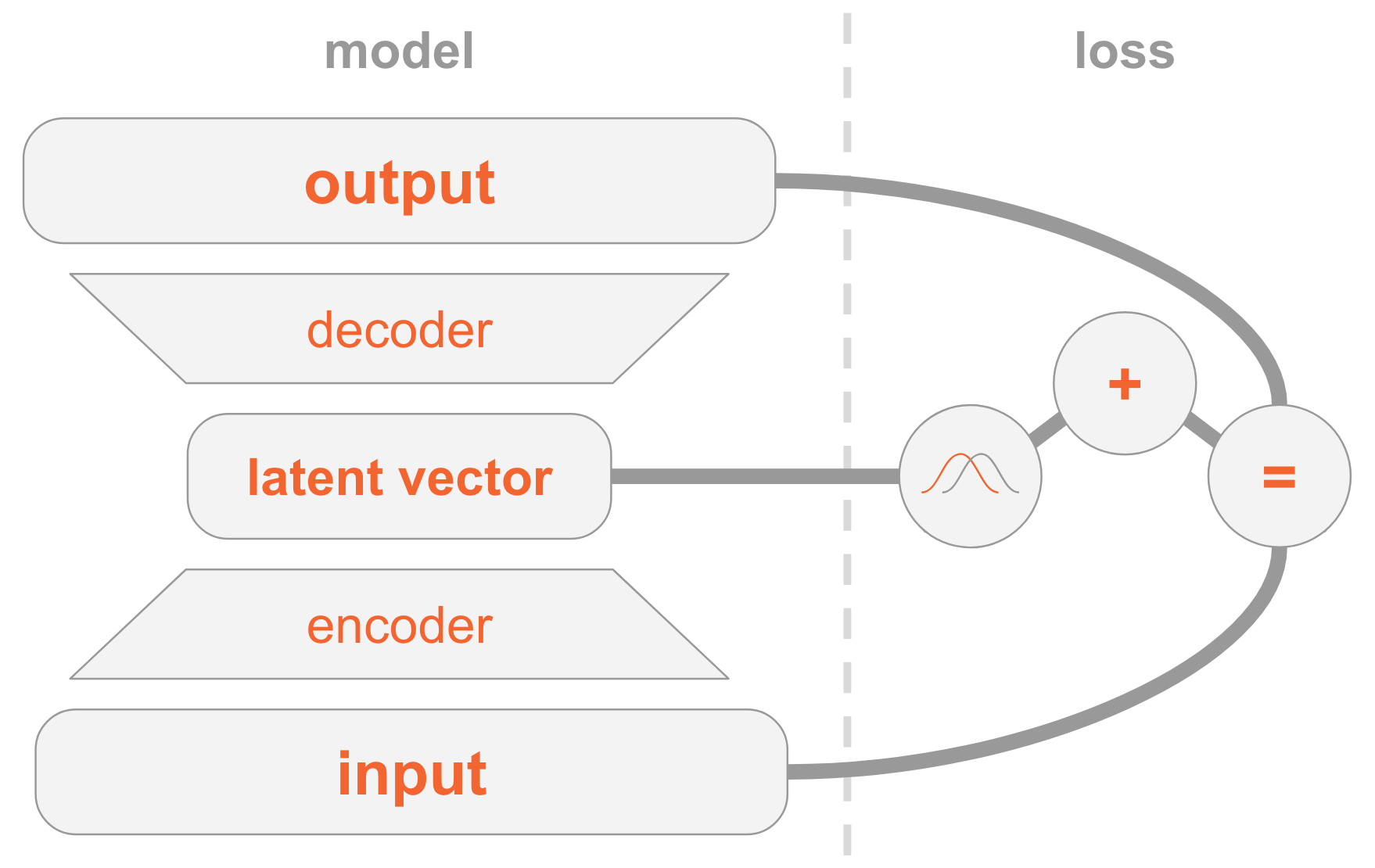
À gauche, nous avons une définition de modèle:

1. L'image d'entrée est transmise via le réseau codeur.
2. L'encodeur fournit des paramètres de distribution $$$Q (z | x)$.
3. Vecteur caché $$$z$tiré de $$$Q (z | x)$. Si l'encodeur est bien formé, alors dans la plupart des cas $$$z$contenir une description $$$x$.
4. Décodeur décode $$$z$dans l'image.

Sur le côté droit, nous avons une fonction de perte:

1. Erreur de récupération: la sortie doit être similaire à l'entrée.
2. $$$Q (z | x)$doit être similaire à la précédente, c'est-à-dire une distribution normale standard multidimensionnelle.

Pour créer de nouvelles images, vous pouvez directement sélectionner le vecteur caché de la distribution précédente et le décoder en image.

Code de travail

Nous allons maintenant étudier la VAE plus en détail et considérer le code de travail. Vous comprendrez tous les détails techniques nécessaires à la mise en œuvre de la VAE. En bonus, je vais vous montrer une astuce intéressante: comment attribuer des rôles spéciaux à certaines dimensions du vecteur caché afin que le modèle commence à générer des images des nombres indiqués.

import numpy as np import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data import matplotlib.pyplot as plt np.random.seed(42) tf.set_random_seed(42) %matplotlib inline 

Je vous rappelle que les modèles sont formés sur MNIST - un ensemble de chiffres manuscrits. Les images d'entrée sont au format $$$\ mathbb {R} ^ {28 × 28}$.

 mnist = input_data.read_data_sets('MNIST_data') input_size = 28 * 28 num_digits = 10 

Ensuite, nous définissons les hyperparamètres.

N'hésitez pas à jouer avec différentes valeurs pour avoir une idée de la façon dont elles affectent le modèle.

 params = { 'encoder_layers': [128], #       'decoder_layers': [128], #    (CNN ,     ) 'digit_classification_layers': [128], #   ,   'activation': tf.nn.sigmoid, #      'decoder_std': 0.5, #   P(x|z)   'z_dim': 10, #    'digit_classification_weight': 10.0, #   ,   'epochs': 20, 'batch_size': 100, 'learning_rate': 0.001 } 

Modèle

Le modèle se compose de trois sous-réseaux:

1. Obtient $$$x$(image), l'encode en une distribution $$$Q (z | x)$dans un espace caché.
2. Obtient $$$z$dans l'espace caché (représentation du code de l'image), la décode en l'image correspondante $$$f (z)$.
3. Obtient $$$x$et détermine le nombre par comparaison avec la couche à 10 dimensions, où la i-ème valeur contient la probabilité du i-ème nombre.

Les deux premiers sous-réseaux sont le fondement de la VAE pure.

La troisième est une tâche auxiliaire qui utilise certaines des dimensions cachées pour coder les nombres trouvés dans l'image. J'expliquerai pourquoi: plus tôt, nous avons discuté du fait que nous ne nous soucions pas des informations que contient chaque dimension de l'espace caché. Un modèle peut apprendre à coder toute information qu'il juge utile pour sa tâche. Étant donné que nous connaissons l'ensemble de données, nous connaissons l'importance de la dimension, qui contient le type de chiffre (c'est-à-dire sa valeur numérique). Et maintenant, nous voulons aider le modèle en lui fournissant ces informations.

Pour un type de chiffre donné, nous l'encodons directement, c'est-à-dire que nous utilisons un vecteur de taille 10. Ces dix nombres sont associés à un vecteur caché, donc lors du décodage de ce vecteur en image, le modèle utilisera des informations numériques.

Il existe deux façons de fournir des modèles vectoriels à codage direct:

1. Ajoutez-le comme entrée au modèle.
2. Ajoutez-le comme étiquette, afin que le modèle lui-même calcule la prévision: nous ajouterons un autre sous-réseau qui prédit un vecteur à 10 dimensions, où la fonction de perte est l'entropie croisée avec le vecteur de codage direct attendu.

Choisissez la deuxième option. Pourquoi? Eh bien, lors du test, vous pouvez utiliser le modèle de deux manières:

1. Spécifiez l'image comme entrée et affichez un vecteur caché.
2. Spécifiez un vecteur caché en entrée et générez une image.

Étant donné que nous voulons prendre en charge la première option, nous ne pouvons pas donner au modèle un chiffre en entrée, car nous ne voulons pas le savoir pendant les tests. Par conséquent, le modèle doit apprendre à le prédire.

 def encoder(x, layers): for layer in layers: x = tf.layers.dense(x, layer, activation=params['activation']) mu = tf.layers.dense(x, params['z_dim']) var = 1e-5 + tf.exp(tf.layers.dense(x, params['z_dim'])) return mu, var def decoder(z, layers): for layer in layers: z = tf.layers.dense(z, layer, activation=params['activation']) mu = tf.layers.dense(z, input_size) return tf.nn.sigmoid(mu) def digit_classifier(x, layers): for layer in layers: x = tf.layers.dense(x, layer, activation=params['activation']) logits = tf.layers.dense(x, num_digits) return logits 

 images = tf.placeholder(tf.float32, [None, input_size]) digits = tf.placeholder(tf.int32, [None]) #        encoder_mu, encoder_var = encoder(images, params['encoder_layers']) #     ,  #     eps = tf.random_normal(shape=[tf.shape(images)[0], params['z_dim']], mean=0.0, stddev=1.0) z = encoder_mu + tf.sqrt(encoder_var) * eps # classify the digit digit_logits = digit_classifier(images, params['digit_classification_layers']) digit_prob = tf.nn.softmax(digit_logits) #     ,  #    decoded_images = decoder(tf.concat([z, digit_prob], axis=1), params['decoder_layers']) 

 #    ,    #    loss_reconstruction = -tf.reduce_sum( tf.contrib.distributions.Normal( decoded_images, params['decoder_std'] ).log_prob(images), axis=1 ) #         . #      , #         #  ,  KL-   # ,    loss_prior = -0.5 * tf.reduce_sum( 1 + tf.log(encoder_var) - encoder_mu ** 2 - encoder_var, axis=1 ) loss_auto_encode = tf.reduce_mean( loss_reconstruction + loss_prior, axis=0 ) # digit_classification_weight      , #      loss_digit_classifier = params['digit_classification_weight'] * tf.reduce_mean( tf.nn.sparse_softmax_cross_entropy_with_logits(labels=digits, logits=digit_logits), axis=0 ) loss = loss_auto_encode + loss_digit_classifier train_op = tf.train.AdamOptimizer(params['learning_rate']).minimize(loss) 

La formation

Nous allons former un modèle pour optimiser deux fonctions de perte - VAE et classification - à l'aide de SGD .

À la fin de chaque époque, nous sélectionnons des vecteurs cachés et les décodons en images pour observer visuellement comment le pouvoir générateur du modèle s'améliore au cours des époques. La méthode d'échantillonnage est la suivante:

1. Définissez explicitement les dimensions qui sont utilisées pour classer par le chiffre que nous voulons générer. Par exemple, si nous voulons créer une image du nombre 2, nous définissons les mesures $$$[0010000000]$.
2. Sélectionnez aléatoirement d'autres dimensions de la distribution normale multidimensionnelle. Ce sont les valeurs des différents nombres générés à cette époque. Nous avons donc une idée de ce qui est codé dans d'autres dimensions, par exemple, le style d'écriture manuscrite.

La signification de l'étape 1 est qu'après la convergence, le modèle devrait être capable de classer la figure dans l'image d'entrée selon ces paramètres de mesure. Cependant, ils sont également utilisés dans la phase de décodage pour créer une image. C'est-à-dire que le sous-réseau du décodeur sait: lorsque les mesures correspondent au numéro 2, il doit générer une image avec ce numéro. Par conséquent, si nous réglons manuellement les mesures sur le nombre 2, nous obtiendrons une image générée de cette figure.

 samples = [] losses_auto_encode = [] losses_digit_classifier = [] with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for epoch in xrange(params['epochs']): for _ in xrange(mnist.train.num_examples / params['batch_size']): batch_images, batch_digits = mnist.train.next_batch(params['batch_size']) sess.run(train_op, feed_dict={images: batch_images, digits: batch_digits}) train_loss_auto_encode, train_loss_digit_classifier = sess.run( [loss_auto_encode, loss_digit_classifier], {images: mnist.train.images, digits: mnist.train.labels}) losses_auto_encode.append(train_loss_auto_encode) losses_digit_classifier.append(train_loss_digit_classifier) sample_z = np.tile(np.random.randn(1, params['z_dim']), reps=[num_digits, 1]) gen_samples = sess.run(decoded_images, feed_dict={z: sample_z, digit_prob: np.eye(num_digits)}) samples.append(gen_samples) 

Vérifions que les deux fonctions de perte semblent bonnes, c'est-à-dire qu'elles diminuent:

 plt.subplot(121) plt.plot(losses_auto_encode) plt.title('VAE loss') plt.subplot(122) plt.plot(losses_digit_classifier) plt.title('digit classifier loss') plt.tight_layout() 

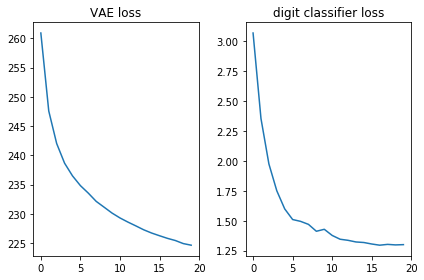
De plus, affichons les images générées et voyons si le modèle peut vraiment créer des images avec des nombres manuscrits:

 def plot_samples(samples): IMAGE_WIDTH = 0.7 plt.figure(figsize=(IMAGE_WIDTH * num_digits, len(samples) * IMAGE_WIDTH)) for epoch, images in enumerate(samples): for digit, image in enumerate(images): plt.subplot(len(samples), num_digits, epoch * num_digits + digit + 1) plt.imshow(image.reshape((28, 28)), cmap='Greys_r') plt.gca().xaxis.set_visible(False) if digit == 0: plt.gca().yaxis.set_ticks([]) plt.ylabel('epoch {}'.format(epoch + 1), verticalalignment='center', horizontalalignment='right', rotation=0, fontsize=14) else: plt.gca().yaxis.set_visible(False) plot_samples(samples) 

Conclusion

C'est agréable de voir qu'un simple réseau de distribution directe (sans circonvolutions fantaisistes) génère de belles images en seulement 20 époques. Le modèle a rapidement appris à utiliser des mesures spéciales pour les nombres: à la 9e ère, nous voyons déjà la séquence de nombres que nous essayions de générer.

Chaque époque a utilisé des valeurs aléatoires différentes pour d'autres dimensions, donc le style est différent entre les époques, mais il est similaire en leur sein: au moins à l'intérieur de certaines. Par exemple, au 18e, tous les chiffres sont plus gros par rapport au 20e.

Remarques

L'article est basé sur mon expérience et les sources suivantes:

• Conclusion variationnelle et apprentissage profond: une nouvelle synthèse
• Guide du codeur automatique de variation