Cours MIT "Sécurité des systèmes informatiques". Conférence 16: «Side Channel Attacks», partie 1

Institut de technologie du Massachusetts. Cours magistral # 6.858. "Sécurité des systèmes informatiques." Nikolai Zeldovich, James Mickens. 2014 année

Computer Systems Security est un cours sur le développement et la mise en œuvre de systèmes informatiques sécurisés. Les conférences couvrent les modèles de menace, les attaques qui compromettent la sécurité et les techniques de sécurité basées sur des travaux scientifiques récents. Les sujets incluent la sécurité du système d'exploitation (OS), les fonctionnalités, la gestion du flux d'informations, la sécurité des langues, les protocoles réseau, la sécurité matérielle et la sécurité des applications Web.

Cours 1: «Introduction: modèles de menace» Partie 1 / Partie 2 / Partie 3
Conférence 2: «Contrôle des attaques de pirates» Partie 1 / Partie 2 / Partie 3
Conférence 3: «Débordements de tampon: exploits et protection» Partie 1 / Partie 2 / Partie 3
Conférence 4: «Séparation des privilèges» Partie 1 / Partie 2 / Partie 3
Conférence 5: «D'où viennent les systèmes de sécurité?» Partie 1 / Partie 2
Conférence 6: «Opportunités» Partie 1 / Partie 2 / Partie 3
Conférence 7: «Native Client Sandbox» Partie 1 / Partie 2 / Partie 3
Conférence 8: «Modèle de sécurité réseau» Partie 1 / Partie 2 / Partie 3
Conférence 9: «Sécurité des applications Web», partie 1 / partie 2 / partie 3
Conférence 10: «Exécution symbolique» Partie 1 / Partie 2 / Partie 3
Conférence 11: «Ur / Web Programming Language» Partie 1 / Partie 2 / Partie 3
Conférence 12: Sécurité du réseau, partie 1 / partie 2 / partie 3
Conférence 13: «Protocoles réseau», partie 1 / partie 2 / partie 3
Conférence 14: «SSL et HTTPS» Partie 1 / Partie 2 / Partie 3
Conférence 15: «Logiciel médical» Partie 1 / Partie 2 / Partie 3
Conférence 16: «Side Channel Attacks» Partie 1 / Partie 2 / Partie 3

Ok les gars, commençons. Donc, aujourd'hui, nous allons parler des attaques par les canaux secondaires, un problème commun inhérent à tous les types de systèmes. Dans un sens large, les attaques par le canal latéral se produisent dans une situation où vous ne pensez pas que certaines informations sont capables de révéler des informations sur votre système.



En règle générale, vous disposez de plusieurs composants qui établissent une connexion entre l'utilisateur et le serveur. En même temps, vous pensez que vous savez tout ce qui passe par ce fil reliant deux abonnés, vous connaissez tous les bits que l'utilisateur et le serveur échangent entre eux, et c'est sûr. Mais il arrive souvent que certaines informations soient toujours divulguées par l'utilisateur ou le serveur. L'exemple décrit dans la conférence d'aujourd'hui décrit une situation où la synchronisation des messages entre l'utilisateur et le serveur révèle des informations supplémentaires que vous ne connaissez pas, simplement en observant le flux binaire entre ces abonnés.

En fait, il existe une classe beaucoup plus large de canaux secondaires dont vous pouvez vous inquiéter. Les gens ont appris l'apparition des canaux latéraux dans les années 40, lorsqu'ils ont découvert que si vous commencez à taper des caractères sur un téléscripteur, l'électronique du téléscripteur commencera à émettre un rayonnement radiofréquence. Dans ce cas, vous pouvez simplement placer l'oscilloscope à côté de lui et observer comment la fréquence du signal radio change en fonction du symbole que l'opérateur de téléscripteur imprime. Ainsi, le rayonnement RF est un exemple classique d'un canal latéral qui vous inquiète.

Il existe de nombreux autres exemples remarqués par les gens, comme la consommation d'électricité. C'est un autre canal latéral dont vous pouvez vous inquiéter, car votre ordinateur utilisera une quantité d'énergie différente en fonction de ce qu'il calcule.



Un exemple de canal latéral est le son, grâce auquel une fuite d'informations est également possible. Par exemple, les gens écoutent l'imprimante et, en fonction des sons qu'ils émettent, ils peuvent dire quels caractères elle imprime. Ceci est particulièrement facile pour les imprimantes matricielles qui produisent des sons très gênants lors de l'impression.

En général, c'est quelque chose à penser. Dans une conférence du lundi, Kevin a également mentionné quelques canaux secondaires intéressants avec lesquels il traite dans ses recherches. Mais nous allons regarder le canal latéral spécifique que David Bramley et Dan Bone ont étudié. Dans leur travail, publié il y a environ 10 ans, ils écrivent qu'ils ont pu extraire la clé cryptographique du serveur Web Apache en mesurant le timing des différentes réponses aux différents paquets d'entrée d'un client hostile. Dans ce cas particulier, ils ont «recherché» une clé cryptographique. En fait, de nombreuses attaques via le canal latéral ciblent des clés cryptographiques en partie parce qu'il est assez difficile d'obtenir une grande quantité de données via un tel canal. Et les clés cryptographiques sont l'une des situations où un petit nombre de bits est émis, c'est-à-dire que pendant une attaque, les attaquants peuvent extraire environ 200 à 256 bits d'informations. Mais en se basant uniquement sur ces 200 bits, ils sont capables de déchiffrer la clé cryptographique de ce serveur Web.

Si vous essayez d'accéder à une sorte de base de données remplie de numéros de sécurité sociale, vous devrez en «fusionner» beaucoup d'informations. C'est pourquoi la plupart des attaques par canal latéral se concentrent sur l'obtention de petits secrets comme les clés cryptographiques ou les mots de passe. Mais en général, cela s'applique à de nombreuses autres situations.

Dans le matériel de cours, une autre chose intéressante est décrite - c'est que tout cela peut être fait sur le réseau. Vous vous êtes probablement rendu compte qu'ils devaient faire beaucoup de travail minutieux pour saisir ces moindres différences dans les informations temporelles. Chaque demande envoyée au serveur diffère d'une autre demande de 1 à 2 microsecondes, ce qui est une période très courte. Par conséquent, vous devez être très prudent, car nos réseaux ne nous permettent pas de détecter une telle différence temporaire et de déterminer que le serveur a traité votre demande pendant 1-2 microsecondes plus longtemps qu'il ne le devrait.



En conséquence, il n'était pas clair si une telle attaque pouvait être organisée dans un réseau très «bruyant», car les informations utiles devaient être séparées du niveau de bruit. Ces gars-là ont été parmi les premiers à montrer que vous pouvez vraiment le faire sur un réseau Ethernet avec un serveur à une extrémité du réseau et un client à l'autre extrémité. Ils ont prouvé qu'il est en effet possible de mesurer ces différences en partie par la moyenne, en partie par d'autres astuces.
Le plan pour le reste de cette conférence est le suivant - nous allons d'abord nous plonger dans les détails de l'algorithme cryptographique à clé publique RSA que ces gars-là ont utilisé. Nous ne l'évaluerons pas du point de vue de la sécurité, mais nous verrons comment il est implémenté, car c'est l'implémentation de l'algorithme qui est critique pour l'utilisation du canal latéral.

Bramley et Bone ont examiné les différents détails de la mise en œuvre afin de comprendre quand certaines choses fonctionnaient plus rapidement ou plus lentement. Nous devons donc d'abord découvrir comment le cryptosystème RSA est implémenté, puis nous reviendrons et découvrirons comment attaquer toutes ces structures disponibles dans RSA.

Commençons par revoir le RSA à un niveau élevé. RSA est un cryptosystème à clé publique assez largement utilisé. Nous avons mentionné ces gars il y a quelques semaines lorsque nous avons parlé de certificats. Maintenant, nous allons voir comment cela fonctionne réellement.

En règle générale, vous devez vous soucier de trois choses: la génération de clés, le chiffrement et le déchiffrement. Dans RSA, la façon de créer une clé est de sélectionner 2 grands nombres premiers, notés p et q. Dans leur article, ces gars écrivent sur p et q chacun avec une taille de 512 bits. Ceci est généralement appelé RSA 1024 bits, car le produit de ces nombres premiers est un entier de 1000 bits. De nos jours, ce n'est probablement pas un bon choix pour la taille de la clé RSA, car la casser est une tâche relativement facile pour les attaquants. Donc, si il y a 10 ans, 1000 bits semblaient une quantité raisonnable, aujourd'hui, lors de la construction d'un système, vous devez choisir une clé RSA de 2000, 3000 ou même 4000 bits. Ainsi, la taille de la clé RSA signifie la taille de ces nombres premiers.

Ensuite, pour plus de commodité, nous parlerons du nombre n, qui est simplement le produit de ces nombres premiers n = pq, et ce nombre est appelé le module. Alors maintenant que nous savons comment créer la clé, ou au moins une partie de la clé, nous devrons trouver comment crypter et décrypter les messages.



Et la façon dont nous allons crypter et décrypter les messages est basée sur l'augmentation de la puissance des nombres modulo n. Cela semble un peu étrange, mais nous le découvrirons dans une seconde. Donc, si vous voulez crypter le message m, vous devez le convertir en m ^e par le mod n. La valeur de e est un degré, dans une seconde nous découvrirons comment le choisir. C'est ainsi que nous allons chiffrer le message.

Autrement dit, nous prenons simplement ce message comme un entier et le portons à une puissance. Dans une seconde, nous verrons pourquoi cela fonctionne, mais pour l'instant, nous désignerons tout ce message chiffré avec la lettre C.

Ensuite, pour le décrypter, nous devons trouver un autre exposant intéressant d, qui nous permet de prendre le message crypté C, de le porter à la puissance d modulo n, et par conséquent, d'obtenir comme par magie le message décrypté m.

Ainsi, le principe général est d'utiliser un exposant pour crypter un message et un autre exposant pour le décrypter.



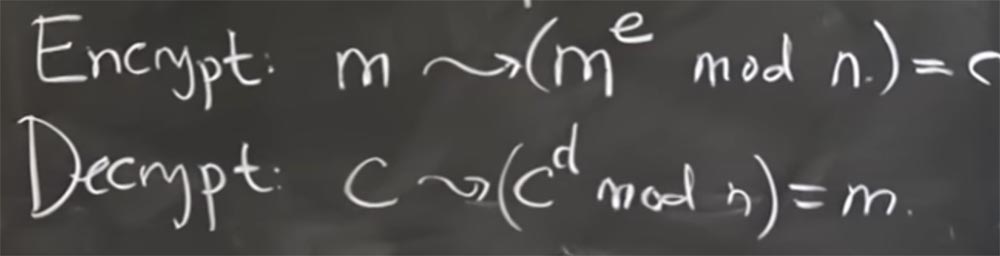
Dans l'ensemble, il semble un peu difficile de comprendre comment nous allons arriver à ces deux nombres magiques qui nous renvoient en quelque sorte le message d'origine. Mais si vous regardez comment l'exponentiation ou la multiplication modulo ce nombre n fonctionne, alors vous comprendrez tout.

Si nous prenons X et l'élevons à la puissance égale à la fonction φ de n, alors ce sera 1 modulo n:

X ^{φ (n)} = 1 mod n

Cette fonction phi pour notre choix particulier de n est assez simple; elle est égale à φ = (p-1) (q-1).
Alors le produit de l'exposant ouvert e, qui est supérieur à 1 mais inférieur à φ (n), par l'exposant secret d, sera égal à:

ed = ɑφ (n) +1, où ɑ est une constante.

Ainsi, il est possible de décrypter correctement le message, car il existe un algorithme assez simple si vous connaissez la valeur de φ (n) pour calculer d en tenant compte de e ou e en tenant compte de d.

Public: 1 module n est-il différent de 1?

Professeur: oui, j'ai fait une erreur ici, l'égalité devrait ressembler à ceci:

X ^{φ (n)} _{mod n} = 1 mod n, c'est-à-dire que la valeur de X dans le degré de la fonction "fi" de n modulo n est égale à l'unité modulo n.

Cela signifie essentiellement que pour RSA, nous devons choisir une valeur e, qui sera notre valeur de cryptage. Ensuite, à partir de e, nous allons générer d sur la base de la formule de = 1 mod φ (n), donc d = 1 / e mod φ (n).



Il existe des algorithmes euclidiens que vous pouvez utiliser efficacement pour ce calcul. Mais pour ce faire, vous devez connaître ce φ (n), qui nécessite une factorisation, c'est-à-dire la factorisation de notre nombre n en facteurs p et q.

Ainsi, RSA est un système où la clé publique est une paire: l'exposant de chiffrement e et le nombre n, et la paire d et n est une clé privée qui est gardée secrète. Ainsi, n'importe qui peut augmenter le pouvoir de le crypter pour vous. Mais vous seul connaissez cette valeur de d et vous pouvez donc déchiffrer le message. Et tant que vous ne connaissez pas la factorisation de ces facteurs P et Q, ou N, égale au produit de P et Q, vous ne savez pas ce qu'est φ = (p-1) (q-1).



Par conséquent, le calcul de cette valeur de d est une tâche assez difficile. C'est à cela que sert l'algorithme RSA de haut niveau.

Maintenant que nous nous sommes familiarisés avec les principes du RSA, je veux m'attarder sur 2 choses. Il y a des astuces sur la façon de l'utiliser correctement et il y a des pièges qui se posent lors de son utilisation. Il existe de nombreuses façons d'implémenter du code pour cette exponentiation et de le faire efficacement. C'est une tâche assez extraordinaire, car nous avons affaire à des entiers de 1000 bits, pour lesquels vous ne pouvez pas simplement exécuter l'instruction de multiplication. Il faudra probablement beaucoup de temps pour terminer ces opérations.

Par conséquent, la première chose que je veux mentionner est les différents pièges de RSA. L'une d'elles est la multiplicité. Supposons que nous ayons 2 messages: m ₀ et m ₁ . Je vais les crypter, transformant m ₀ en m ₀ ^e mod n, et m1 en m ₁ ^e mod n. Un problème possible, ou plutôt, pas nécessairement un problème, mais une surprise désagréable pour quelqu'un qui utilise RSA est qu'il est très facile de crypter le produit m ₀ par m ₁ , car vous multipliez simplement ces 2 chiffres: m ₀ ^e mod n * m ₁ ^e mod n.



Si vous les multipliez, vous vous retrouverez avec le produit (m ₀ m ₁ ) ^e module. Il s'agit d'un chiffrement correct avec une utilisation simplifiée de RSA pour la valeur m ₀ m ₁ . Ce n'est pas un gros problème pour le moment, car vous pouvez simplement créer ce message crypté, mais vous n'êtes pas en mesure de le décrypter. Cependant, il est possible qu'un système commun vous permette de décrypter des messages spécifiques. Autrement dit, si cela vous permet de déchiffrer le message que vous avez créé, alors peut-être qu'en suivant le chemin inverse, vous pouvez découvrir quels sont ces messages m ₀ et m ₁ .

Ce fait ne doit pas être ignoré, car il affecte un certain nombre de protocoles utilisant RSA. Il y a une propriété que nous utiliserons comme mécanisme de défense à la fin de notre conférence.

Le deuxième écueil, ou propriété RSA, auquel vous devez prêter attention est le déterminisme ou la déterminabilité. Dans l'implémentation élémentaire décrite précédemment, si vous prenez le message m et le cryptez, le transformant en m ^e mod n, alors c'est une fonction de message déterministe. Par conséquent, si vous le cryptez à nouveau, vous obtiendrez exactement le même cryptage.

Ce n'est pas une propriété souhaitable, car si je vois que vous envoyez un message chiffré à l'aide de RSA et que je veux savoir de quoi il s'agit, il peut être difficile pour moi de le déchiffrer. Mais je peux essayer différentes choses, à la suite de quoi je vois que vous envoyez ce message.

Ensuite, je vais le crypter et voir si vous obtenez le même texte crypté. Et si oui, alors je découvrirai que vous avez chiffré. Parce que tout ce dont j'ai besoin pour crypter un message est une clé publique accessible au public, qui est une paire de chiffres (n, e).

Ce n'est donc pas très bien, et vous devrez peut-être faire attention à cette propriété lorsque vous utilisez RSA. Ainsi, les primitives de ce type sont difficiles à utiliser directement.



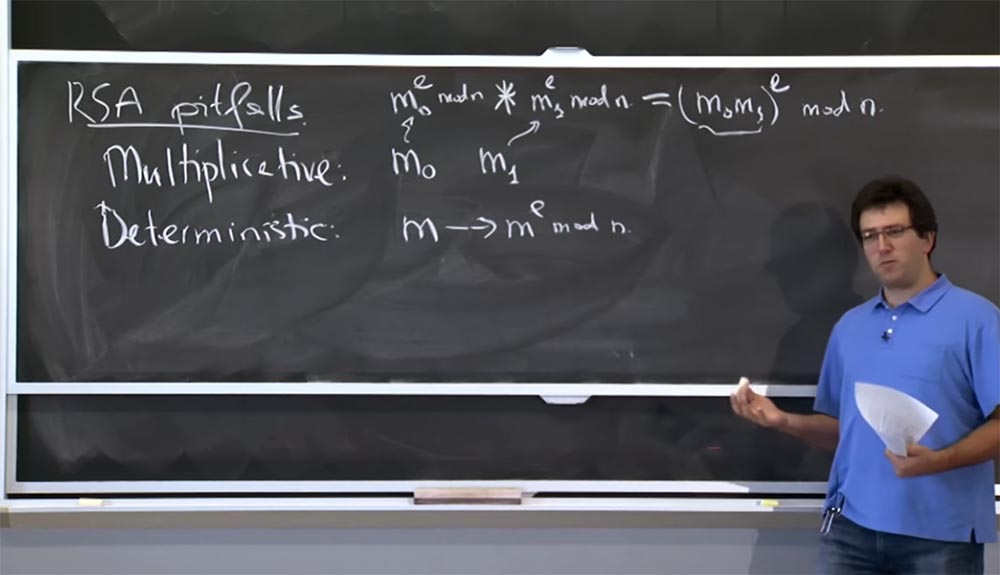
En pratique, afin d'éviter des problèmes similaires avec RSA, les gens codent le message d'une certaine manière avant le chiffrement. Au lieu d'élever directement un message à une puissance, ils prennent une sorte de fonction de message et l'élèvent à un module de puissance:

(f (m)) ^e mod n.

Cette fonction f, couramment utilisée aujourd'hui, est appelée OAEP - Optimal Asymmetric Encryption with Addition. C'est quelque chose encodé avec deux propriétés intéressantes.

Premièrement, cela apporte de l'aléatoire. Vous pouvez considérer f (m) comme générant un message de 1000 bits que vous allez crypter. Une partie de ce message sera votre message m ici au milieu de ce rectangle. Bien sûr, vous pouvez le récupérer lors du décryptage. Donc, il y a 2 choses intéressantes que vous voulez faire: à droite, vous placez une sorte d'aléatoire, la valeur de r. Cela donne que si vous cryptez un message plusieurs fois, vous obtiendrez des résultats différents à chaque fois, donc le cryptage ne sera plus déterminé.

Afin de surmonter cette propriété multiplicative et d'autres types de problèmes, sur la gauche, vous avez un pad pad, qui est une séquence de type 1 0 1 0 1 0. Vous pouvez choisir une meilleure séquence, mais en gros, c'est une sorte de séquence prévisible, qui vous insérez ici et chaque fois que vous déchiffrez le message, vous vous assurez que cette séquence est toujours là. La multiplication détruira ces bits de tampon, puis il sera clair pour vous que quelqu'un a foiré votre message et l'a rejeté. Si ces bits restent en place, cela prouve que personne n'a falsifié votre message et que vous pouvez le recevoir, car il a été correctement chiffré par quelqu'un.



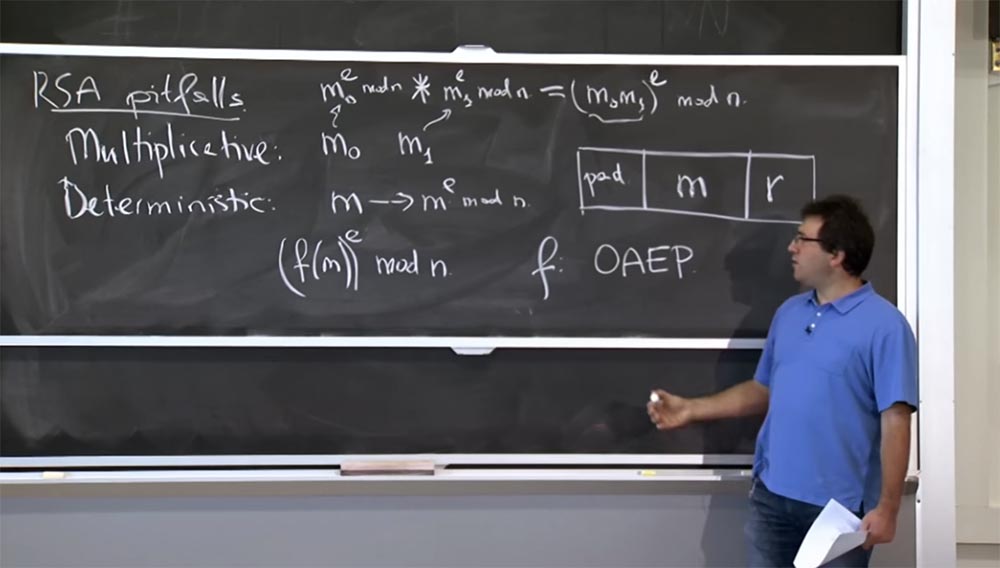Public: si un attaquant sait quelle est la valeur du pad, peut-il mettre 1 tout en bas de la séquence puis multiplier cette valeur?

Professeur: oui, peut-être. C'est un peu compliqué, car ce caractère aléatoire r continuera. La conception spécifique de cet OAEP est donc un peu plus compliquée que ce que j'ai décrit. Mais imaginez qu'il s'agit d'une multiplication plutôt que d'un bit, le caractère aléatoire s'étend plus loin, vous pouvez donc créer un schéma OAEP dans lequel cela ne se produira pas.

Il s'avère que vous ne devez pas utiliser directement ce calcul RSA, dans la pratique, vous devez utiliser une sorte de bibliothèque qui implémente toutes ces choses pour vous de la bonne manière, et l'utiliser comme paramètre de chiffrement et de déchiffrement.

Cependant, les détails discutés ci-dessus seront utiles pour nous, car nous essayons en fait de comprendre comment casser ou attaquer l'implémentation RSA existante.

En particulier, l'attaque décrite dans l'article de conférence profitera du fait que le serveur est sur le point de tester ce module complémentaire de remplissage lorsqu'il reçoit le message. C'est donc ainsi que nous allons considérer le temps qu'il faudra au serveur pour décrypter. , m . .

, pad, . , , , , : RSA, , . , . , .

, , RSA. , , , . , , , 1000 . e .



, . , 1000 . 1000- , 1000 1000 n, . RSA , .
4 , . , . , CRT. . . , , , , [ = a ₁ ] mod p [ = a ₂ ] mod q, q – , .



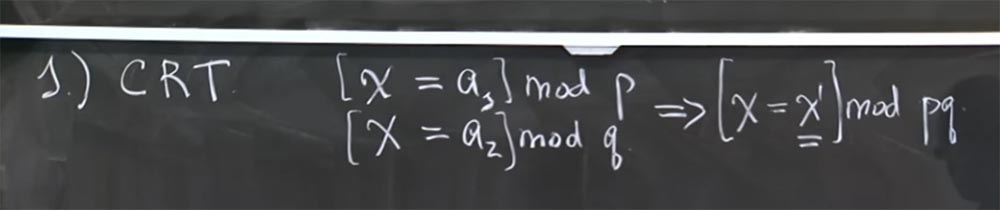
, [ = ¹ ] mod pq. ¹ , . ¹ , mod pq a ₁ a ₂ mod p q.

, ? , , n, p q.



, mod pq, mod p mod q. , , mod pq. , ? , , ?

: , ?

: , , , . , p q, n 1000 , p q 500 , . , , — , , . — . , , . 1000 512 , 2 . , 4 . [ = a ₁ ] mod p [ = a ₂ ] mod q , 4 . 2 RSA , .

, .

, Sliding windows, « ». . , .



, - , 500 , mod p mod q, d. c d? , c d . d , 500, . , , . , « ». .

c ^2x , : (c ^x ) ² :

c ^2x = (c ^x ) ²

c ^2x , 2 , cx, . , , c ^2x+1 :

c ^2x+1 = (c ^x ) ² x

.

, , , . , , , . , .

« », ? , . , , « » c ^2x+1 = (c ^x ) ² x .

, , , – , c ^2x+1 c ^2x , c. , , . , .



, :

1
3
7
...
31

. , , , .

, ^32x+y , 5 , 32- , ^y .



³² . , , , , c . «» .

29:00

Cours MIT "Sécurité des systèmes informatiques". 16: « », 2


.

Merci de rester avec nous. Aimez-vous nos articles? Vous voulez voir des matériaux plus intéressants? Soutenez-nous en passant une commande ou en le recommandant à vos amis, une réduction de 30% pour les utilisateurs Habr sur un analogue unique de serveurs d'entrée de gamme que nous avons inventés pour vous: Toute la vérité sur VPS (KVM) E5-2650 v4 (6 cœurs) 10 Go DDR4 240 Go SSD 1 Gbps à partir de 20 $ ou comment diviser le serveur? (les options sont disponibles avec RAID1 et RAID10, jusqu'à 24 cœurs et jusqu'à 40 Go de DDR4).

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps , .

Dell R730xd 2 fois moins cher? Nous avons seulement 2 x Intel Dodeca-Core Xeon E5-2650v4 128 Go DDR4 6x480 Go SSD 1 Gbps 100 TV à partir de 249 $ aux Pays-Bas et aux États-Unis! Pour en savoir plus sur la création d'un bâtiment d'infrastructure. classe utilisant des serveurs Dell R730xd E5-2650 v4 coûtant 9 000 euros pour un sou?