Cours MIT "Sécurité des systèmes informatiques". Conférence 16: Attaques par le canal latéral, partie 2

Institut de technologie du Massachusetts. Cours magistral # 6.858. "Sécurité des systèmes informatiques." Nikolai Zeldovich, James Mickens. 2014 année

Computer Systems Security est un cours sur le développement et la mise en œuvre de systèmes informatiques sécurisés. Les conférences couvrent les modèles de menace, les attaques qui compromettent la sécurité et les techniques de sécurité basées sur des travaux scientifiques récents. Les sujets incluent la sécurité du système d'exploitation (OS), les fonctionnalités, la gestion du flux d'informations, la sécurité des langues, les protocoles réseau, la sécurité matérielle et la sécurité des applications Web.

Cours 1: «Introduction: modèles de menace» Partie 1 / Partie 2 / Partie 3
Conférence 2: «Contrôle des attaques de pirates» Partie 1 / Partie 2 / Partie 3
Conférence 3: «Débordements de tampon: exploits et protection» Partie 1 / Partie 2 / Partie 3
Conférence 4: «Séparation des privilèges» Partie 1 / Partie 2 / Partie 3
Conférence 5: «D'où viennent les systèmes de sécurité?» Partie 1 / Partie 2
Conférence 6: «Opportunités» Partie 1 / Partie 2 / Partie 3
Conférence 7: «Native Client Sandbox» Partie 1 / Partie 2 / Partie 3
Conférence 8: «Modèle de sécurité réseau» Partie 1 / Partie 2 / Partie 3
Conférence 9: «Sécurité des applications Web», partie 1 / partie 2 / partie 3
Conférence 10: «Exécution symbolique» Partie 1 / Partie 2 / Partie 3
Conférence 11: «Ur / Web Programming Language» Partie 1 / Partie 2 / Partie 3
Conférence 12: Sécurité du réseau, partie 1 / partie 2 / partie 3
Conférence 13: «Protocoles réseau», partie 1 / partie 2 / partie 3
Conférence 14: «SSL et HTTPS» Partie 1 / Partie 2 / Partie 3
Conférence 15: «Logiciel médical» Partie 1 / Partie 2 / Partie 3
Conférence 16: «Side Channel Attacks» Partie 1 / Partie 2 / Partie 3

Public: comment déterminer d'abord x et y?

Professeur: pour cela vous devez regarder l'exposant en représentation binaire. Supposons que j'essaie de calculer la valeur de c ^1011010 , le degré peut également consister en un plus grand nombre de bits. Si nous voulons faire un re-squaring, alors nous devons regarder le bit le plus bas - ici c'est 0.



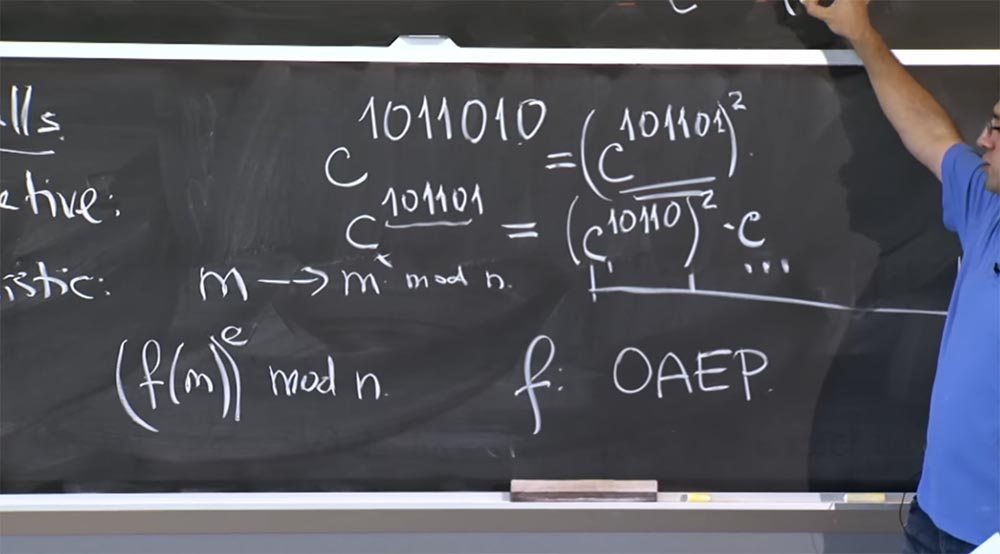
Ainsi, nous obtenons l'égalité c ^1011010 = (c ¹⁰¹¹⁰¹ ) ²

Ensuite, nous devons calculer c ¹⁰¹¹⁰¹ , ici nous ne pouvons pas utiliser cette règle, car ce n'est pas 2x - ce sera x plus 1. Par conséquent, nous écrivons cette égalité:

c ¹⁰¹¹⁰¹ = (c ¹⁰¹¹⁰ ) ² c, car ce préfixe 101101 = 10110 + 1.

Par conséquent, nous multiplions le carré par c, nous l'utilisons donc pour recadrer.

Pour les "fenêtres coulissantes", nous devons capturer plus de bits de l'extrémité inférieure. Si vous voulez faire un tour ici avec une «fenêtre coulissante» au lieu d'en extraire un s d'ici, alors en tenant compte de cette immense table, nous pouvons prendre 3 bits à la fois, en nous accrochant à c7. Si nous prenons les 3 premiers bits d'un degré, nous obtenons c ¹⁰¹¹⁰¹ = (c ¹⁰¹ ) ⁸ c ¹⁰¹ .

Dans ce cas, nous avons vraiment le même nombre de calculs pour (c ¹⁰¹ ) ⁸ , mais vous pouvez voir la valeur de c ¹⁰¹ dans le tableau. Et la partie sous la forme (c ¹⁰¹ ) ⁸ dit que vous allez utiliser des «fenêtres coulissantes» pour calculer sa valeur.



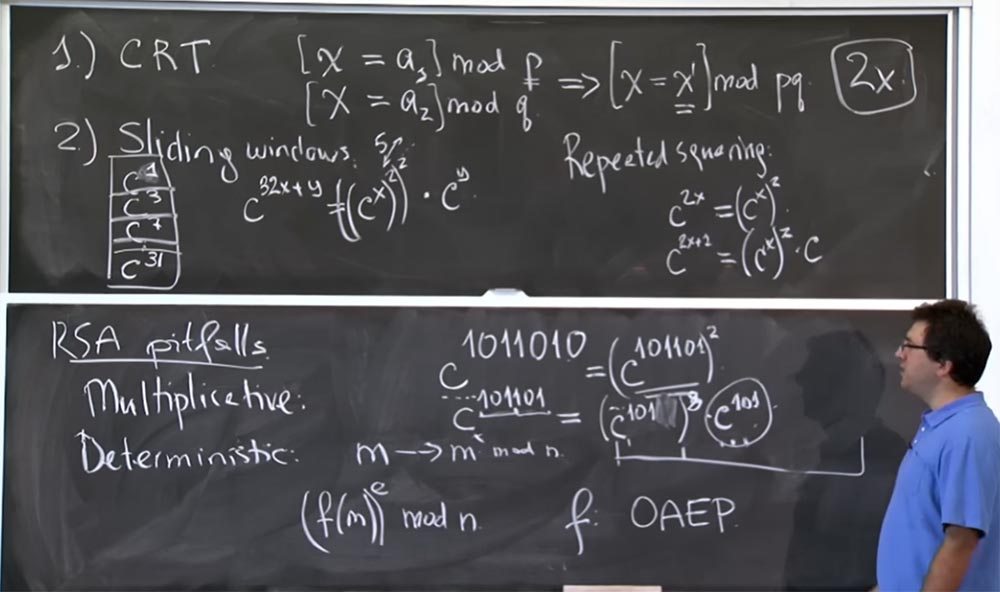
Cela fait gagner beaucoup de temps, car il permet d'utiliser des valeurs pré-multipliées. Il y a 10 ans, on pensait qu'une table de valeurs jusqu'à 32 degrés était le plan optimal en termes d'efficacité de calcul, car il y a une sorte de compromis ici, non? Vous passez du temps à créer ce tableau, mais il ne doit pas être trop volumineux si vous n'utilisez pas souvent certains enregistrements. Supposons que si vous créez une table de valeurs jusqu'à ⁵⁰⁰ degrés C, mais que vous n'utiliserez pas d'exposants avec une valeur supérieure à 128, alors perdez simplement votre temps.

Public: y a-t-il une raison de ne pas créer une telle table géante à l'avance? Autrement dit, pour calculer les valeurs d'un nombre limité de degrés qui peuvent être contournés dans les calculs?

Professeur: si vous ne voulez pas effectuer de calculs volumétriques à l'avance ... eh bien, il y a deux choses. La première est que vous devriez alors avoir un code pour vérifier si l'enregistrement requis dans le tableau est plein ou non, et cela réduira probablement la précision de la prévision des branches des processus CPU. Dans le même temps, dans le cas général, le processeur fonctionnera plus lentement, car il devra vérifier si l'enregistrement requis est dans la table. La deuxième chose, qui est quelque peu gênante, pourrait être la fuite des entrées de table via divers canaux secondaires, à savoir via les modèles d'accès au cache. Donc, si vous avez un autre processus en cours d'exécution sur le même processeur, vous pouvez voir quelles adresses de cache sont supprimées du cache ou ralenties car quelqu'un a accès à l'enregistrement c ³ ou à l'enregistrement c ³¹ . Et plus cette table est grande, plus il est facile de déterminer quels bits d'exposant sont utilisés pour créer la clé RSA.

Cette table géante est capable de dire quelle adresse de cache a été perdue pour le processeur, c'est-à-dire, indique que le processus de cryptage devrait avoir accès à cette entrée dans la table. À son tour, cela vous indique que la séquence de bits donnée apparaît dans l'exposant de votre clé privée. Par conséquent, je suppose que mathématiquement, vous pouvez remplir ce tableau autant que nécessaire, mais en pratique, vous ne voulez pas qu'il se révèle être de taille gigantesque. De plus, vous ne pourrez pas utiliser efficacement d’énormes entrées de table. Il est beaucoup plus utile d'utiliser les enregistrements d'une table relativement petite à plusieurs reprises, par exemple, pour calculer c ^7, vous pouvez utiliser la valeur c ³ deux fois et ainsi de suite.

Voici donc l'optimisation RSA par recalibrage et méthodes de «fenêtre coulissante». Je ne sais pas s'ils utilisent toujours cette taille de "fenêtres coulissantes", mais en tout cas cela accélère le processus de calcul, car sinon il faudrait mettre au carré chaque bit de l'exposant puis multiplier par chaque bit. Par conséquent, si vous avez un exposant de 500 bits, vous devrez compléter 500 carrés et environ 256 multiplications par c. Avec les «fenêtres coulissantes», vous devez encore faire 512 carrés, car cela ne peut être évité, mais le nombre de multiplications par c passera de 256 à environ 32 en raison de l'utilisation des entrées du tableau.

Il s'agit du plan d'optimisation général, qui accélère le processus de calcul d'environ une fois et demie. Il s'agit d'une optimisation assez simple. Il existe deux astuces intelligentes avec des nombres qui rendent le processus de multiplication plus efficace.

La première est la transformation de Montgomery, dans une seconde, nous verrons pourquoi cela est particulièrement important pour nous. Cette optimisation essaie de résoudre un problème pour nous, c'est que chaque fois que nous faisons la multiplication, nous obtenons un nombre qui continue de croître et de croître dans un ordre croissant. En particulier, dans les «fenêtres coulissantes» et dans la mise au carré, vous avez en fait multiplié 2 nombres ensemble lorsque vous avez élevé c à la puissance de y.

Le problème est que si les données d'entrée c ^x et c ^y pour la multiplication étaient, disons, 512 bits chacune, alors la taille du résultat de la multiplication serait de 1000 bits. Après cela, vous prenez ce résultat de 1000 bits et le multipliez à nouveau par quelque chose comme 512 bits, il devient la taille de 1500, 2000, 2500 bits et tout grandit et grandit.

Cependant, vous ne le souhaitez pas, car la multiplication augmente l'ordre des nombres multipliés. Pour cette raison, nous devons garder notre taille numérique aussi petite que possible, fondamentalement égale à 512 bits, car tous ces calculs sont mod p ou mod q.

Nous pouvons réduire ce nombre, disons, nous voulons calculer (((c ^x ) ² ) ² ) ² . Ce que vous pourriez faire, par exemple, est de calculer cx modulo p, puis de le quadriller à nouveau modulo p et de nouveau au carré modulo p. Cette méthode est relativement bonne, car elle nous permet de garder la taille de notre nombre à l'intérieur de 512 bits, c'est-à-dire aussi petite que possible. C'est bien dans le sens de réduire la taille des nombres qu'il faut multiplier, mais en fait, le fonctionnement avec ce module p «augmente considérablement le coût» du calcul.



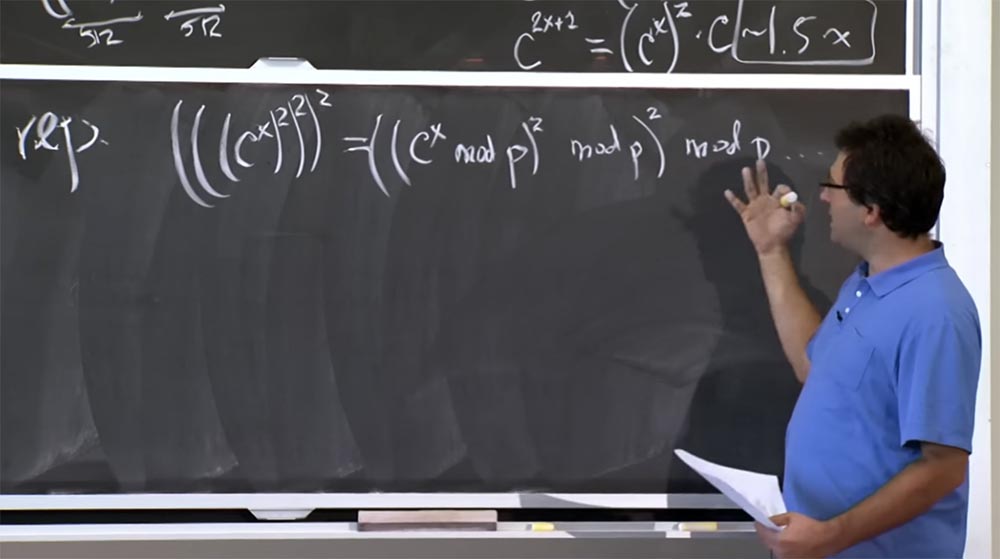
Parce que la façon dont vous obtenez le mod p est en division. Et la division est pire que la multiplication. Je ne vais pas énumérer les algorithmes de division, mais c'est très lent. Habituellement, vous essayez d'éviter autant que possible les opérations de division, car ce n'est pas une programmation facile. Le fait est que vous devez utiliser une sorte d'algorithmes d'approximation, les méthodes de Newton et similaires, et tout cela ralentira le processus de calcul.

La multiplication est beaucoup plus rentable, mais l'utilisation d'opérations mod p ou mod q pour réduire la taille des nombres coûtera plus cher que la multiplication. Je vais vous montrer un moyen d'éviter cela et comment faire des calculs rapides à l'aide de la transformation de Montgomery.

L'idée de base est de représenter les entiers que vous allez multiplier sous la forme d'une transformée de Montgomery. C'est en fait très simple. Pour ce faire, nous multiplions simplement notre nombre a par une certaine valeur magique R. Après une seconde, je vais vous dire ce que c'est. Mais découvrons d'abord ce qui se passe lorsque nous sélectionnons une valeur arbitraire de R.

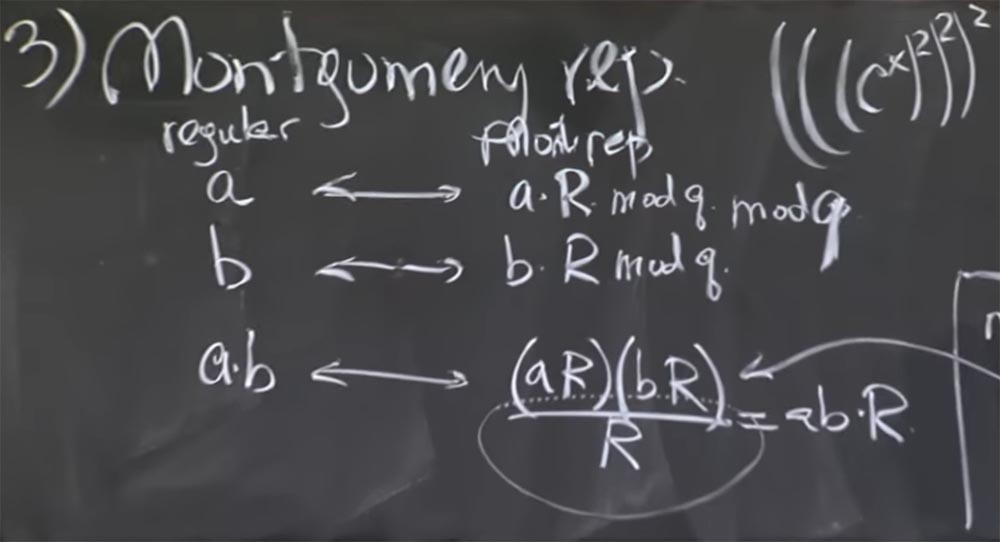
Donc, nous prenons 2 nombres, a et b, et les convertissons en représentation de Montgomery, en multipliant chacun par R. Ensuite, le produit de a et b dans la transformée de Montgomery ressemblera à ceci:

ab <-> (aR) (bR) / R = abR

Autrement dit, vous multipliez aR par bR et vous obtenez le produit de ab par R au carré. Maintenant, nous avons deux R, c'est un peu ennuyeux, mais vous pouvez le diviser par R. En conséquence, nous obtenons le produit de ab par R. On ne sait pas pourquoi nous avons dû multiplier ce nombre encore une fois. Voyons d'abord si cela est vrai, puis nous comprendrons pourquoi ce sera plus rapide.
C'est correct dans le sens où c'est très facile. Si vous souhaitez multiplier certains nombres, vous devez les multiplier par cette valeur de R et obtenir la transformation de Montgomery. Chaque fois que nous multiplions ces 2 nombres, nous devons les diviser par R, puis regarder la forme résultante de la transformation de la forme abR. Ensuite, lorsque nous aurons terminé la quadrature, la multiplication et toutes ces choses, nous retournerons à la forme normale et ordinaire du résultat, en divisant simplement par R pour la dernière fois.



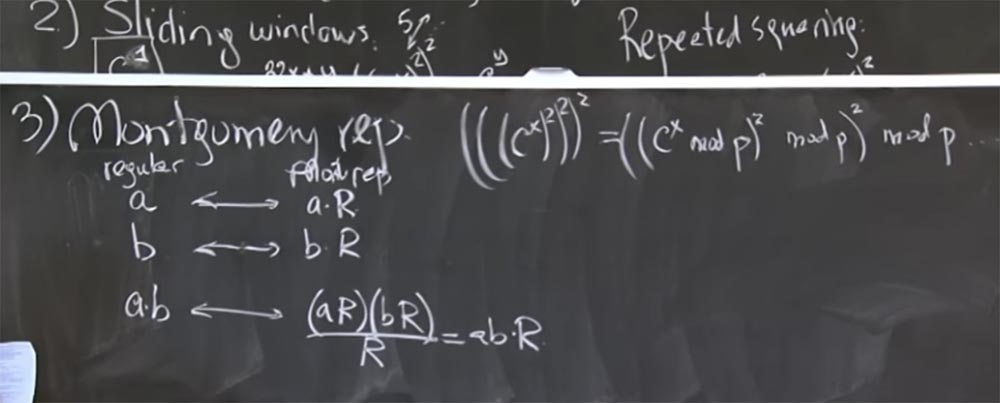
Considérez maintenant comment choisir le nombre le plus approprié pour R pour faire de la division par R une opération très rapide. Et le plus cool ici, c'est que si la division par R est très rapide quand c'est un petit nombre, et qu'on n'a pas à faire ce mod q trop souvent. En particulier, aR, disons, aura également une taille d'environ 500 bits, car tout cela est en fait mod p ou mod q. Ainsi, aR est de 500 bits, bR sera également de 500 bits, de sorte que le produit (aR) (bR) sera de 1000 bits. R sera également un nombre pratique de 500 bits, la taille de p. Et si nous pouvons rendre l'opération de division assez rapide, le résultat de ab sera également approximativement un nombre de 500 bits, afin que nous puissions multiplier sans avoir besoin de division supplémentaire. La division par R est beaucoup plus rentable et nous donne un petit résultat, ce qui évite l'utilisation de mod p dans la plupart des situations.

Alors, quel est ce numéro R étrange dont je parle tout le temps? Il a une valeur de 2 à 512 degrés:

R = 2 ⁵¹²

Ce sera 1 et un tas de zéros, il est donc facile de multiplier par un tel nombre, car il suffit d'ajouter simplement un tas de zéros au résultat. La division peut également être simple si les bits les moins significatifs du résultat sont nuls. Donc, si vous avez une valeur à partir d'un tas de bits accompagné de 512 zéros, alors la division par 2 à 512 degrés sera très simple - vous déposez simplement les zéros sur le côté droit, et c'est une opération de division complètement correcte.

Le petit problème est que nous n'avons en fait pas de zéros sur le côté droit lorsque vous effectuez cette multiplication. Nous avons de vrais nombres de 512 bits utilisant tous les 512 bits.

Le produit de (aR) par (bR) est également un nombre réel de l'ordre de 1000 bits, nous ne pouvons donc pas simplement supprimer les bits les moins significatifs. Mais une approche raisonnable est basée sur le fait que la seule chose qui nous inquiète est la valeur du mod p. Ainsi, vous pouvez toujours ajouter plusieurs p à cette valeur sans changer son équivalent mod p. Par conséquent, nous pouvons ajouter des multiples de valeurs p de sorte que tous les bits les moins significatifs deviennent des zéros. Regardons quelques exemples simples. Je ne vais pas écrire 512 bits sur la carte, mais je ne donnerai qu'un court exemple.

Supposons que dans notre situation R = 2 ⁴ = 10000. C'est une taille beaucoup plus petite qu'elle ne l'est réellement. Voyons comment fonctionne cette transformation Montgomery. Nous essayons de calculer le mod q, où q = 7. Sous forme binaire, q = 7 est (111).

Supposons en outre que nous avons effectué une certaine multiplication (aR) (bR), et en représentation binaire le résultat est 11010, c'est-à-dire que ce sera la valeur du produit (aR) (bR). Comment le divisons-nous par R?

De toute évidence, les quatre bits les moins significatifs ne sont pas tous des zéros, nous ne pouvons donc pas simplement les séparer, mais nous pouvons ajouter des quantités qui sont des multiples de q. En particulier, on peut ajouter 2 fois en q, avec 2q = 1110 en représentation binaire. À la suite de l'addition, nous obtenons 101000, j'espère avoir tout fait correctement.



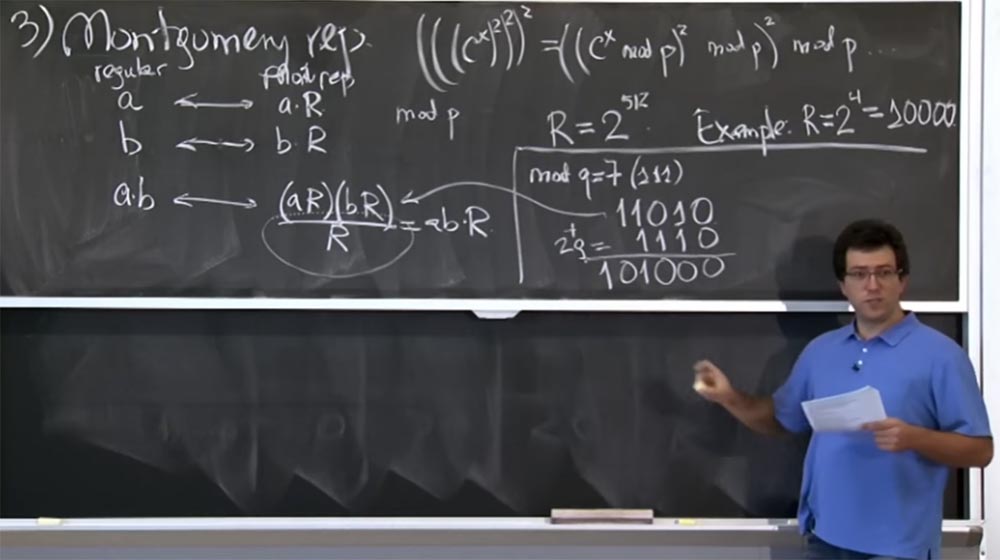
Nous avons donc obtenu la somme (aR) (bR) + 2q. En fait, nous ne nous soucions pas de + 2q, car tout ce qui nous intéresse est la valeur de mod q. Nous sommes maintenant plus proches de l'objectif, car nous avons trois zéros à droite. Maintenant, nous pouvons ajouter un peu plus q. Disons que cette fois, ce sera 8q, ce qui sera 111000. Encore une fois, additionnez nos lignes et obtenez 1100000. Maintenant, nous avons l'original (aR) (bR) + 2q + 8q = 1100000. Enfin, nous pouvons très facilement diviser cette chose en R, laissant simplement tomber quatre zéros bas.



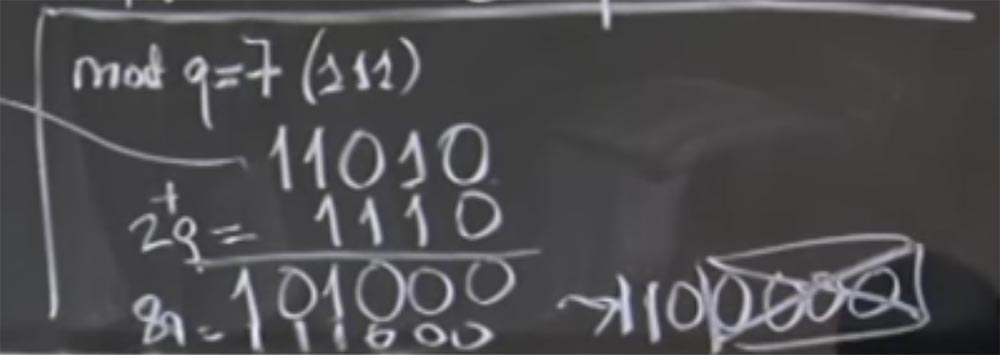Public: le produit (aR) (bR) se terminera toujours avec 1024 zéros?

Professeur: non, et je vais vous expliquer quelle pourrait être la confusion. Disons que le nombre a est de 512 bits, nous l'avons multiplié par R et obtenu un nombre de 1000 bits. Dans ce cas, vous avez raison, aR est le nombre dans lequel les bits hauts sont a et les bits bas sont tous des zéros. Mais ensuite, nous exécutons le mod q pour le réduire. Par conséquent, la taille de 1024 bits est généralement une coïncidence, car ce nombre n'a ces faibles zéros que lors de la première conversion, mais après quelques multiplications, il s'agira de bits arbitraires.

Afin de ne pas vous induire en erreur, j'ai dû écrire le mod q ici après aR et après bR - ici je l'ajoute - et calculer ce mod q dès que vous faites la conversion pour réduire la valeur.



La conversion initiale est plutôt laborieuse, ou au moins aussi coûteuse que la modulation conventionnelle en multiplication. Ce qui est cool, c'est que vous payez ce prix une fois lorsque vous effectuez la conversion Montgomery, puis, au lieu de le reconvertir à chaque étape des calculs, vous le conservez simplement sous la forme d'une vue Montgomery.
N'oubliez pas que pour atteindre une puissance de 512 bits, vous devrez faire plus de 500 multiplications, car nous devons faire au moins 500 carrés et quelques autres. Donc, vous modifiez deux fois q et vous obtenez ensuite de nombreuses opérations de division simples si vous restez dans cette forme de représentation des nombres. Et à la fin, vous faites une division par R pour revenir à ce formulaire ab.

Donc, au lieu de faire mod q 500 fois pour chaque étape de la multiplication, vous faites mod q deux fois et continuez ensuite à faire ces divisions par R à un coût minimal.
Public: lorsque vous ajoutez des multiples de q puis divisez par R, avons-nous un reste?
Professeur: en fait, mod q signifie le reste lorsque vous divisez par q. Autrement dit, x + yq mod q = x. Dans ce cas, il existe une autre propriété utile: tous les modules sont des nombres premiers. Cela est aussi vrai que le fait que si vous avez (x + yq / R) mod q, alors il est égal à x / R mod q.



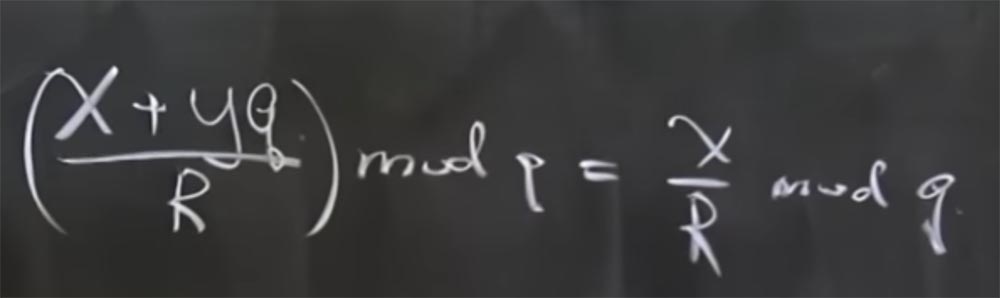
La raison de penser ainsi est qu'il n'y a pas de véritables opérations de division en arithmétique modulaire, c'est juste une inversion. En fait, cela signifie que si nous avons (x + yq) multiplié par R inversé calculé par mod q, alors il est égal à la somme de deux produits: le produit x du R inversé par mod q et le produit de yq par le R inversé par mod q. De plus, le dernier terme est réduit, car c'est quelque chose multiplié par q.



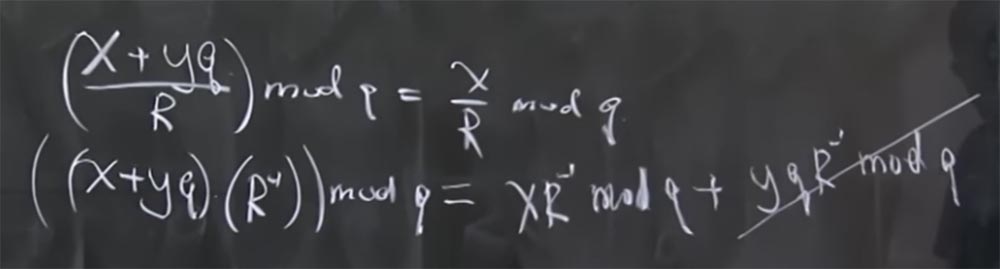
Pour des choses comme la somme de 2q, 8q, etc., il existe une formule qui accélère le processus de calcul. Je l'ai fait progressivement, d'abord calculé 2q, puis 8q et ainsi de suite, mais les supports de cours ont une formule complète qui peut être utilisée, je ne veux pas perdre de temps à l'écrire au tableau. Il vous permet de calculer le multiple de q que vous devez ajouter pour que tous les bits les moins significatifs se transforment en 0. Ensuite, il s'avère que pour faire la division par R, il vous suffit de calculer ce multiple magique de q, de l'ajouter, puis de jeter le bas zéro bit, et cela ramènera votre nombre à 512 bits quelle que soit la taille du résultat que vous obtenez.

Mais il y a une subtilité. La seule raison pour laquelle nous en parlons est parce que quelque chose de drôle se passe ici, ce qui nous permet de trouver des informations sur les horaires. En particulier, bien que nous ayons divisé par R, nous savons toujours que le résultat sera d'environ 512 bits. Mais il peut toujours être supérieur à q, car q n'est pas un nombre de 512 bits, il peut être légèrement inférieur à R.

Il se peut donc qu'après avoir fait cette division avantageuse par R, nous devrons peut-être soustraire à nouveau q, car nous obtenons quelque chose de petit, mais toujours pas assez petit. Il y a donc une chance qu'après cette division, nous devions de nouveau soustraire q. Et cette soustraction peut être utilisée dans le cadre de l'attaque, car l'opération de soustraction ajoute le temps de calcul.



Et quelqu'un a découvert - pas ces gars-là, mais quelqu'un dans le travail précédent - qu'il y avait une chance de faire quelque chose appelé réduction supplémentaire, ou réduction supplémentaire. , . , xd mod q, - x mod q, 2R. .



, x mod q , . , cd.



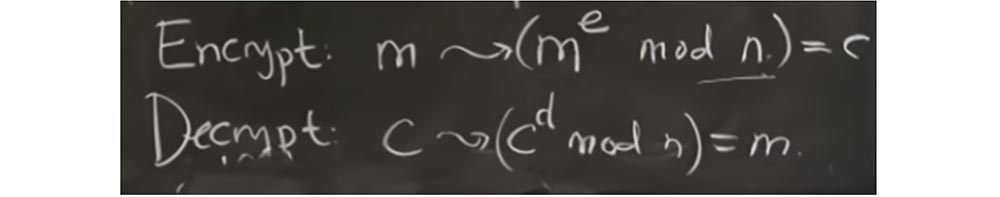
, extra reduction , X , , , q.



, c, extra reduction , c — q. , , q . , extra reduction, , , X mod q , = q + έ, . , . , , , , extra reduction .

: , ?

: , extra reduction? , , , . , . , , extra reduction, , , . , . , , mod q. , , , . , mod q , , .

, . , - , . — , . , - , extra reduction .

, . , OpenSSL, , . , mod q . , , .

, , , , a b. — 512- . , 32- , , 64- ? ?



- ? , , a b .

, , 512 , 64- , 32- . a : a ₁ a ₀ , a ₀ , a ₁ — . b – b ₁ b ₀ .

ab 3- : a ₁ b ₁ , a ₀ b ₀ , a ₁ b ₀ + a ₀ b ₁ . .



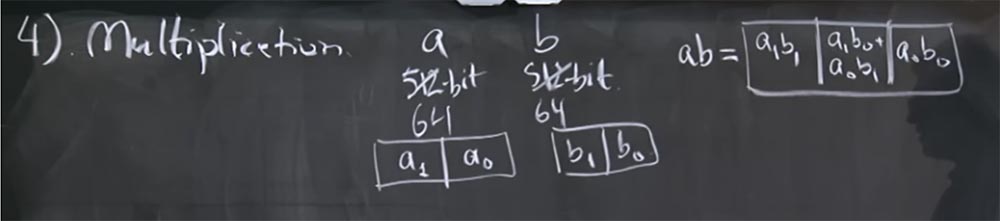
55:00

Cours MIT "Sécurité des systèmes informatiques". 16: « », 3


La version complète du cours est disponible ici .

Merci de rester avec nous. Aimez-vous nos articles? Vous voulez voir des matériaux plus intéressants? Soutenez-nous en passant une commande ou en le recommandant à vos amis, une réduction de 30% pour les utilisateurs Habr sur un analogue unique de serveurs d'entrée de gamme que nous avons inventés pour vous: Toute la vérité sur VPS (KVM) E5-2650 v4 (6 cœurs) 10 Go DDR4 240 Go SSD 1 Gbps à partir de 20 $ ou comment diviser le serveur? (les options sont disponibles avec RAID1 et RAID10, jusqu'à 24 cœurs et jusqu'à 40 Go de DDR4).

VPS (KVM) E5-2650 v4 (6 cœurs) 10 Go DDR4 240 Go SSD 1 Gbit / s jusqu'en décembre gratuitement en payant pour une période de six mois, vous pouvez commander ici .

Dell R730xd 2 fois moins cher? Nous avons seulement 2 x Intel Dodeca-Core Xeon E5-2650v4 128 Go DDR4 6x480 Go SSD 1 Gbps 100 TV à partir de 249 $ aux Pays-Bas et aux États-Unis! Pour en savoir plus sur la création d'un bâtiment d'infrastructure. classe utilisant des serveurs Dell R730xd E5-2650 v4 coûtant 9 000 euros pour un sou?